6.5 Parabolas的应用

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 适用Parabolas

  Collapse Expand

  适用Parabolas

  播放段落

  Kelly is nearly done with the chapter on in her math class. She has become pretty familiar with the general shape of a parabola , and has started noticing the use of parabolas all around her. One thing that she hasn't figured out yet is why satellite-TV dishes are 3D parabolas. She is sure it isn't a coincidence, but doesn't know what it is about a parabolic shape that is important.
  ::Kelly几乎完成了数学课的章节。 她已经非常熟悉抛物线的一般形状, 并开始注意到在她周围使用抛物线。 一件事她还没有搞清楚为什么卫星电视盘是3D帕拉波拉斯。 她确信这不是巧合, 但是她不知道抛物线的形状是什么, 这很重要。

  播放段落

  Do you know?
  ::你知道吗?

  播放段落

  Applications of Parabolas
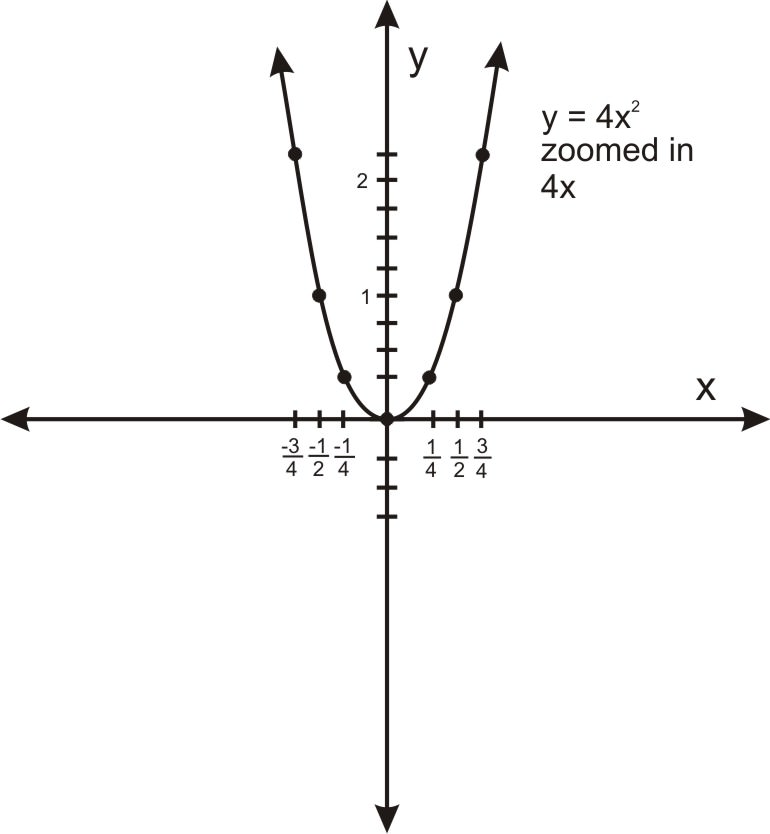
  ::适用Parabolas

  播放段落

  There is a very interesting property of parabolas. This is the fact that all parabolas have the same shape . Or, in the language of geometry, any two parabolas are similar to one another. This means that any parabola can be scaled in or out to produce another parabola of exactly the same shape. This may come across as surprising, because parabolas where $\begin{align*}x^2\end{align*}$ has a large coefficient certainly look much “steeper” than parabolas with a small coefficient when examined over the same domain, as shown in the graphs below.
  ::Parabolas 具有非常有趣的属性。 这是所有 parabolas 都具有相同形状的事实。 或者, 以几何语言来说, 任何两个parbolas 都相似 。 这意味着任何 parbola 都可以 缩放 或 排出 来产生另一个完全相同形状的 parbola 。 这可能令人惊讶, 因为 如下图所示, 以 x2 计高系数的 parabolas 明显比以小系数的parbolas 看上去“ 更“ 坚固 ” 。

  a. Tall and skinny:		b. Short and wide:

  播放段落

  But when one of the parabolas is scaled appropriately, these parabolas are identical:
  ::但当其中一种抛物体适当缩放时,这些抛物体是相同的:

  a. Tall and skinny - zoomed in by 4x:		b. Short and wide:

  播放段落

  This fact about parabolas can be seen from an algebra standpoint given the fact that all parabolas are generated from a line and a point not on that line. This configuration of generating objects, a line and a point, is always the same shape. Any other line and point looks exactly the same—simply zoom in or out until the line and point are the same distance from one another. So the shapes that any two such configurations generate must also be the same shape.
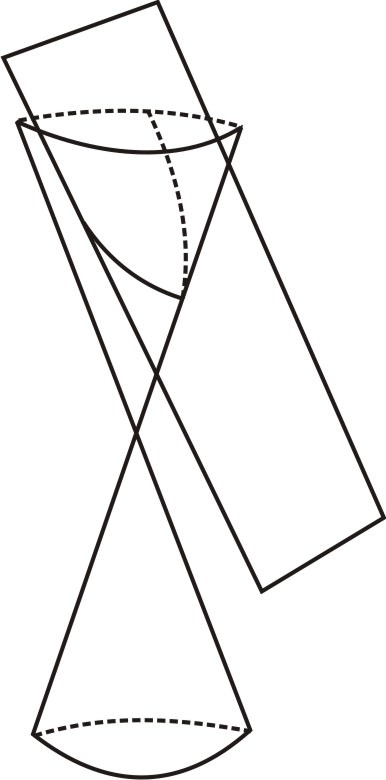
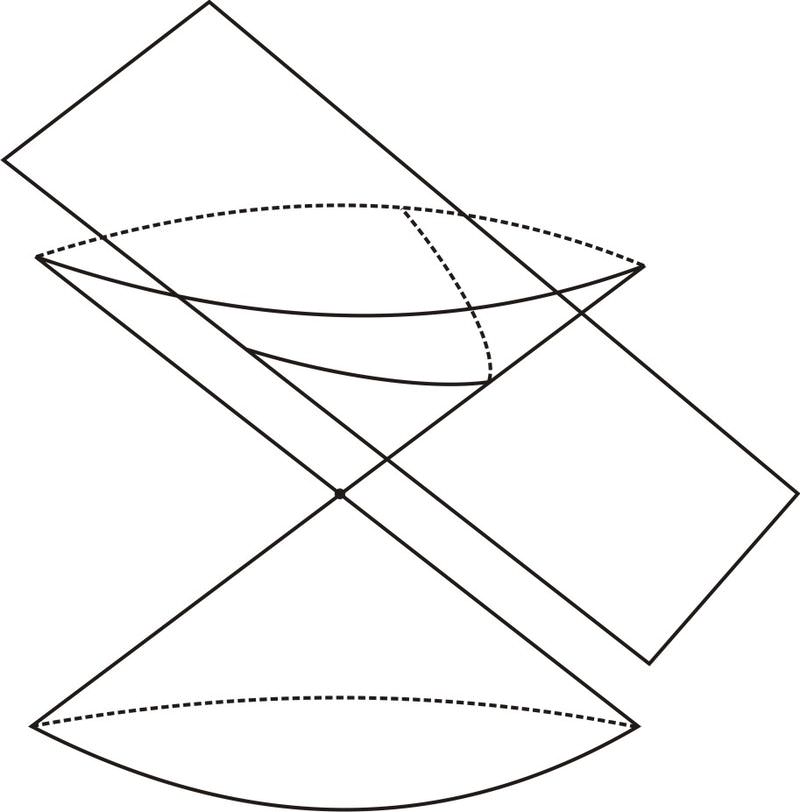
  ::关于parabolas 的这个事实可以从代数角度看出来,因为所有 parabolas 都是从线上产生的, 而不是从线上产生的。 这种生成对象、 线和点的配置总是相同的形状。 任何其它的线和点看起来都完全相同—— 简单缩放到线和点之间的距离相同。 因此, 任何两种这样的配置生成的形状也必须是相同的形状 。

  播放段落

  From an analytic geometry standpoint, there were two factors that might affect the shape of the parabola. The first is the distance between the cutting plane and the apex of the cone. But cones have the same proportions at any scale, so no matter what this distance, the picture can be reduced or enlarged, affecting this distance but not the shape of the cone or plane. So this parameter does not actually change the shape of the conic section that results. The other factor is the shape of the actual cone. This is its steepness, defined by the angle at the apex, or equivalently by the ratio between the radius and the height at any point. This is a bit trickier. It’s not at all obvious that short, squat cones and tall, skinny cones would produce parabolas of the same shape.
  ::从分析几何角度看,有两个因素可能影响抛光线的形状。 第一个因素是切割平面和锥体顶点之间的距离。 但锥体在任何比例上都有相同的比例, 所以不管这种距离如何, 图片可以缩小或扩大, 影响这种距离, 但不会影响锥体或平面的形状。 因此这个参数实际上不会改变所生成的锥体部分的形状。 另一个因素是实际锥体的形状。 这是它的陡峭性, 由顶点的角度来定义, 或与任何点的半径和高度之间的比例相当。 这是一个小的诡计。 很明显的是, 短、 蹲下、 高、 瘦的锥体会产生相同形状的副作用。

  a. Tall and skinny:		b. Short and wide:

  播放段落

  According to what we found, any parabola produced by slicing any cone resulted in an equation of this form:
  ::根据我们发现的情况,通过切除任何锥体而产生的任何抛物线都会产生这种形式的等式:

  播放段落

  $$\begin{align*}y = ax^2\end{align*}$$
  ::y=ax2 y=ax2 y=ax2

  播放段落

  We want to show that if we generate two such parabolas, that they actually have the same shape. So suppose we use two cone constructions and come up with these parabolas: $\begin{align*}y= a_1 x^2\end{align*}$ and $\begin{align*}y = a_2 x^2\end{align*}$ . We want to show there is some scale factor, call it $\begin{align*}f\end{align*}$ , that shrinks or enlarges $\begin{align*}y= a_1 x^2\end{align*}$ into $\begin{align*}y = a_2 x^2\end{align*}$ . To keep a shape the same, the scale factor needs to affect both the $\begin{align*}x-\end{align*}$ and $\begin{align*}y-\end{align*}$ variables. So we need to find an $\begin{align*}f\end{align*}$ such that $\begin{align*}(fy) = a_1(fx)^2\end{align*}$ is equivalent to $\begin{align*}y = a_2 x^2\end{align*}$ . The first equation can be written $\begin{align*}y = (a_1 f)x^2\end{align*}$ , which is equivalent to the second equation when $\begin{align*}a_1 f = a_2\end{align*}$ , or when $\begin{align*}f = \frac{a_2}{a_1}\end{align*}$ . Such an $\begin{align*}f\end{align*}$ always exists for non-negative numbers $\begin{align*}a_1\end{align*}$ and $\begin{align*}a_2\end{align*}$ . So the parabolas are indeed the same shape. If $\begin{align*}a\end{align*}$ is less than zero, then the parabola can be reflected vertically to produce a parabola of the same shape and with positive coefficient $\begin{align*}a\end{align*}$ .
  ::我们想要显示,如果我们产生两个这样的parabolas, 它们实际上具有相同的形状。 所以假设我们使用两个锥形构造, 并得出这些参数 : y=a1x2 和 y=a2x2。 我们想要显示, 某个比例系数, 称为 f, 缩放或放大 y=a1x2 进入 y=a2x2 。 要保持一个形状不变, 比例系数需要同时影响 x- 和 y- 变量。 因此我们需要找到一个 f , 这样( fy) =a1 (f) 2 等于 y=a2x2 。 第一个方程式可以写为 y= (a1f)x2 , 相当于 a1f=a2 或 f=a2 的第二个方形。 这样, 非负数 a1 和 a2 总是存在这样的方形。 因此, parbolas 的形状确实是相同的。 如果一个不小于零, 那么 , 那么 parbola 可以垂直反射镜可以被反射为垂直反射出相同的形状和正系数 。

  播放段落

  Parabola Applications
  ::帕拉波拉应用

  播放段落

  Burning Mirrors
  ::燃烧镜

  播放段落

  Diocles ( $\begin{align*}\sim 240-180\end{align*}$ BCE) was a mathematician from Ancient Greece about whom we know very little. However, we know enough from a few scant documents that he thought about an important application of parabolas. It comes from what is sometimes called the “optical property” of parabolas. Remember the optical property of : lines from one focus “bounce off” the side of the ellipse to hit the other focus.
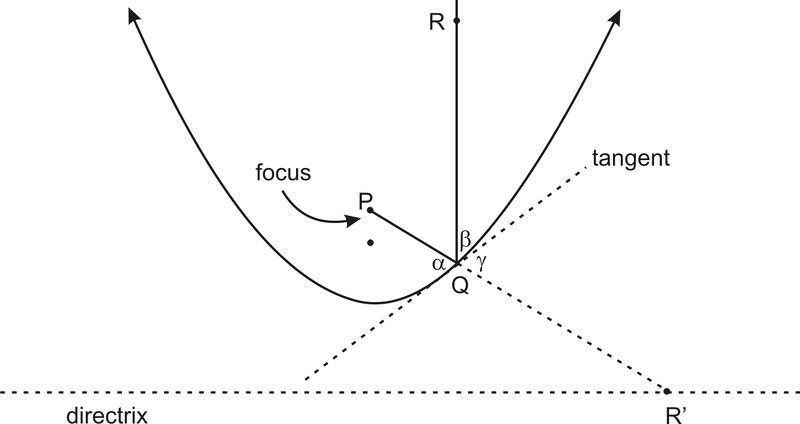
  ::迪奥克利斯(240-180-BCE)是一位来自古希腊的数学家,我们对此知之甚少,然而,我们从很少的文件中知道的足够多,他认为它是对parapolas的重要应用。它来自有时被称为parapolas的“光属性 ” 。 记住光学属性:从极地侧的焦点“反弹”到击中另一个焦点的线。

  播放段落

  For parabolas, since parabolas have only one focus, the directrix plays a role. For the parabola, the optical property is that lines perpendicular to the directrix “bounce off” the parabola and converge at the focus. Or, alternatively, lines from the focus “bounce off” off the parabola and continue perpendicular to the directrix. As with the ellipse, “bouncing off” means that the two lines meet the parabola at equal angles to the tangent.
  ::对于抛光灯,由于抛光灯只有一个焦点,直线发挥作用。对抛光灯而言,光学特性是直线“反射”抛光灯直线的直线,在焦线上趋近。或者,从抛光灯的“反射”线到焦线的“反射”线,继续直线的直线。和椭圆一样,“反射”意味着两条直线在正切线的同等角度上与抛光线相匹配。

  

  播放段落

  In the above diagram, the optical property states that $\begin{align*}\Box \ \alpha \cong \Box \ \beta\end{align*}$ . The proof is similar to the proof of the optical property of ellipses. In the above diagram $\begin{align*}P\end{align*}$ is the focus and $\begin{align*}Q\end{align*}$ is a point on the parabola. Let $\begin{align*}R'\end{align*}$ be the point on the directrix that is obtained by extending $\begin{align*}PQ\end{align*}$ . Then $\begin{align*}PR'\end{align*}$ , the straight line, is clearly the shortest distance between $\begin{align*}P\end{align*}$ and $\begin{align*}R'\end{align*}$ that passes through the tangent line. Let $\begin{align*}R\end{align*}$ be on the line lying directly above $\begin{align*}Q\end{align*}$ such that $\begin{align*}QR = QR'\end{align*}$ . The $\begin{align*}R\end{align*}$ can be thought of as $\begin{align*}R'\end{align*}$ , reflected across the tangent line. Then $\begin{align*}\Box \ \alpha \cong \Box \ \gamma\end{align*}$ (vertical angles) and $\begin{align*}\Box \ \gamma \cong \Box \ \beta\end{align*}$ (reflected angles), and so $\begin{align*}\Box \ \alpha \cong \Box \ \beta\end{align*}$ (transitive property).
  ::在上述图表中,光学属性显示,该证据与椭圆的光学属性的证明相似。在上图P中,焦点是焦点,Q是抛物线上的点。让R 成为通过扩展 PQ 获得的准点。然后,光线PR 明显是P 和R 之间的最短距离,穿过正切线。让R 直接停留在Q 上方的线上,如QR 。R 可以被认为是R , 反射在正切线上。然后是 (垂直角度) 和 (反向角度) , 以及 (反向角度) 和 (反向角度) 以及 (透明属性) 。

  播放段落

  The optical property has some interesting applications. Diocles described one potential application in his document “On Burning Mirrors”. He envisioned a parabolic-shaped mirror (basically a parabola rotated about its line of symmetry) which would collect light from the sun and focus it on the focal point, creating enough of a concentration of light to start a fire at that point. Some claim that Archimedes attempted to make such a contraption with copper plates to fight the Romans in Syracuse.
  ::光学特性有一些有趣的应用,Diocles在他的“关于燃烧的镜子”的文件中描述了一种潜在的应用。 他设想了一种抛物线形镜(基本上按对称线旋转的抛物线),从太阳中收集光,将光集中在焦点上,创造出足够的光浓度,从而在那个时候点起火。 一些人声称Archimedes试图用铜板制造这样的装置,在锡拉库兹与罗马人作战。

  播放段落 Headlights:  The optical property is also responsible for parabola-shaped unidirectional lights, such as car headlights. If a bulb is placed at the focus of a parabolic mirror, the light rays reflect off the mirror parallel to each other, making a focused beam of light. ::灯头:光学特性还负责抛光灯形状单向灯,例如汽车灯头。如果灯泡放在抛光镜的焦点,光线会反射镜子的平行,产生有焦点的光束。		播放段落 Cassegrain Telescopes:  Satellite telescopes take advantage of the optical property of parabolas to collect as much light from a distant star as possible. The dish of the satellite below is parabolic in shape and reflects light to the point in the middle. ::Cassebrain望远镜:卫星望远镜利用parapolas的光学特性,尽可能从遥远的恒星收集更多的光。下面的卫星天线是抛物线,向中点反映光线。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked a question about why satellite-TV dishes are 3D parabolas.
  ::早些时候,有人问过你为什么卫星电视盘子是3D帕拉波拉斯。

  播放段落

  The satellite dish is a 3D parabola so that all of the signal it collects over a wide area will be concentrated at the focus of the parabola, significantly increasing the reception.
  ::卫星天线是3D抛物线,因此它收集到的广面积的所有信号将集中在抛物线的焦点,从而大大增加接收量。

  播放段落

  Example 2
  ::例2

  播放段落

  Explain why not all ellipses are similar the way parabolas are. While enlarging or shrinking doesn’t work to make two ellipses identical, how can you change the view of two ellipses that have different shapes so that they look the same?
  ::解释为什么所有的省略号都和parabolas相似。 虽然扩大或缩小并不能使两个省略号完全相同,但如何改变两种形状不同的省略号的观点,使其看起来都一样呢?

  播放段落

  The eccentricity of ellipses defines the shape, so when the eccentricity is different for two ellipses, the ellipses are not similar to one another. Viewing one of the ellipses at an angle, however, changes the perceived eccentricity of that ellipse, and the angle can be chosen to match the perceived eccentricity to the eccentricity of the other ellipse, producing an image that is similar to the other ellipse.
  ::椭圆的偏心性决定了外形,所以当两种椭圆的偏心性不同时,椭圆就不同了。 但是,从一个角度看待一个椭圆,可以改变这种椭圆的偏心性,可以选择这个角度来将另一种椭圆的偏心性与另一种椭圆的偏心性相匹配,产生一种类似于另一种椭圆的图像。

  播放段落

  Example 3
  ::例3

  播放段落

  If nothing was used to deflect light before it entered a "burning mirror," where would the sun have to be in relationship to you and the place you want to start a fire? Why is this a constraint? Design a way to circumvent this constraint.
  ::如果在光进入“燃烧的镜子”之前,没有任何东西被用来使光线偏转,那么太阳与你的关系和你想点火的地方会在哪里?为什么这是限制?设计一种方法来绕过这种限制。

  播放段落

  The fire-locale must lie on the segment between you and the sun. This is a problem because to start a ground fire, you would have to wait until evening when the sun is low in the sky so you could aim your lens at the ground, unfortunately the sun is not as bright in the evening so you would lose a significant amount of power. A lens or mirror that changes the angle of the suns rays could help you work around this constraint.
  ::火灾地点必须位于您和太阳之间的部分。 这是一个问题, 因为要引发地面火灾, 您必须等到晚上太阳在天空中低落的时候, 才能将镜头瞄准地面, 不幸的是, 晚上的太阳没有那么亮, 这样你就会失去大量的能量。 改变太阳光线角度的镜头或镜子可以帮助您围绕这个限制进行工作 。

  播放段落

  Example 4
  ::例4

  播放段落

  In the above diagram of a car headlight, the lens directs the beams of light downwards, to keep them out of the eyes of oncoming drivers, if that was the only purpose of the lens, alternatively the lens could be omitted and the headlight could just be angled down slightly. But there is another purpose to the lens. What is it?
  ::在汽车头灯的上图中,镜头引导光束向下,使其远离即将到来的驾驶员的眼睛,如果这是镜头的唯一目的的话,则镜头可以省略,头灯只能稍微向下。但是镜头还有另一个目的。它是什么?

  播放段落

  The lens also expands the array of light which is why it is called “dispersed light.” Without the lens, the headlight would only illuminate a strip the width of the headlight itself, which would not be very useful for driving.
  ::透镜还扩大了光的阵列,这就是为什么它被称为“分散的光 ” 。 没有透镜,头灯只会照亮头灯本身的宽度,这对驾驶没有多大用处。

  播放段落

  Example 5
  ::例5

  播放段落

  A satellite dish antenna is to be constructed in the shape of a paraboloid. The paraboloid is formed by rotating the parabola with focus at the point (25, 0) and directrix $\begin{align*}x = -25\end{align*}$ about the x-axis, where x and y are in inches. The diameter of the antenna is to be 80 inches.
  ::卫星天线的形状是:卫星天线,将卫星天线以抛物体的形式构造,其形成方式是旋转抛物体,以点(25,0)和轴轴x轴xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

  播放段落
  1. Find the equation of the parabola and the domain of x.
     ::查找抛物线的方程和 x 的域 。

  播放段落

  $\begin{align*}x = \frac{1}{100} y^2\end{align*}$
  ::x=1100y2

  播放段落

  The domain is the positive real number set.
  ::域是正实际数设置 。

  播放段落
  2. Sketch the graph of the parabola, showing the location of the focus.
     ::绘制抛物线图,显示焦点位置。

  

  播放段落
  3. A receiver is to be placed at the focus. The designer has warned that a user or installer should take care, the receiver would hit the ground and could be damaged if the antenna were placed "face-down". Determine algebraically whether this observation is correct.
     ::接收器应放在焦点位置。 设计师警告说, 用户或安装者应该小心, 接收器会撞击地面, 如果天线被“ 向下 ” 放置, 可能会损坏。 确定此观察是否正确 。

  播放段落

  Yes, as discovered in part a and shown in the graph of part b, the focus is at x = 25, while the dish only extends to x = 16.
  ::是,如在部分a中发现并在部分b的图表中显示的那样,焦点是 x = 25,而盘子仅延伸至 x = 16。

  播放段落

  Review
  ::回顾

  播放段落
  1. A football player is standing on a hill that is 200 feet above sea-level he throws the football with an initial vertical velocity of 96 feet per second. After how many seconds will the ball reach its maximum height above sea level? What is the maximum height?
     ::足球运动员站在一个海平面200英尺以上的山上,他以最初的垂直速度以96英尺/秒的速度将足球抛出。球在达到海平面最高高度几秒钟后会达到多少秒?最高高度是多少?最高高度是多少?
  播放段落
  2. A shot-gun is discharged vertically upward at a height of 3 feet above the ground. If the bullet has an initial muzzle velocity of 200 feet per second, what maximum height will it reach before it starts to fall to the ground? a) 628 feet b) 1,878 feet c) 20.87 feet d) 199.33 feet
     ::如果子弹最初的枪口速度为每秒200英尺,那么子弹在落地之前会达到何种最大高度? a) 628英尺(b) 1 878英尺(c) 20.87英尺(d) 199.33英尺。
  播放段落
  3. An over-zealous golfer hits a flop shot with a sand wedge to get out of the corner of a sand trip with an initial vertical velocity of 45 feet per second. What is the maximum height that the golf ball will reach? 
     ::一个超热闹的高尔夫球手用沙子挡板打中了一球,然后以最初的垂直速度为每秒45英尺的垂直速度走出沙子之旅的角落。高尔夫球能达到的最高高度是多少?
  播放段落
  4. You are standing on the top of a 1680 ft tall hill, and throw a small ball upwards. At every second, you measure the distance of the ball from the ground. Exactly t seconds after you throw the object, its height, (measured in feet) is $\begin{align*} h (t) = -16t^2 + 256t + 1680\end{align*}$ a) Find $\begin{align*}h(3)\end{align*}$ the ball position 3 seconds after you throw it. b) How much does the object travel during the two seconds between 5 seconds and 7 seconds? c) How long does it take for the object to reach a height of 2640 ft? d) How long does it take for the object to hit the ground?
     ::你站在一个1680英尺高高的山顶上,向上扔一个小球。 每秒,你都要测量球与地面的距离。在投出物体后整整几秒钟,其高度(以脚计)是h(t)16t2+256t+1680a),在投出该物体后3秒钟找到h(3)球位置。b)物体在5秒至7秒之间的两秒钟内飞行多少时间?c)物体达到2640英尺高度需要多长时间?d)物体撞击地面需要多长时间?
  播放段落
  5. A student participating in a game of kick ball kicked the ball with an initial vertical velocity of 32 feet per second. Its height above the earth in feet is given by $\begin{align*}s(t) = -16t^2 + 32t\end{align*}$ where t is time in seconds. What is the maximum height reached by the ball? HINT - Graph the parabola (you only need to worry about the section where $\begin{align*}0 \leq t \leq 2\end{align*}$ or rewrite the equation to find the vertex.
     ::参加踢球游戏的学生以32英尺/秒的初始垂直速度踢球。 它的脚高度由 s(t) 16t2+32t 给出, 其中时间为秒。 球达到的最大高度是多少? HINT - 绘制抛物线( 您只需要担心 0. t2 或重写方程式以找到顶点的区段 ) 。
  播放段落
  6. An arch over the entrance to an enchanted trail has a parabolic shape, the arch has a height of 25 feet and it is 30 feet between the support pillars. Find an equation that models the arch, using the x-axis to represent the ground of the park. State the focus and directrix.
     ::被迷惑的通道入口的拱门有抛物线形状, 拱门的高度为25英尺, 在支持柱之间的高度为30英尺。 找到一个方程式来模拟拱门, 使用 X 轴来代表公园的地面 。 显示焦点和指针 。
  播放段落
  7. A satellite dish has a parabolic shape with a diameter of 80 meters. The collected tv signals are focused on a single point, called the "focal" point, which is the focus of the paraboloid (the cross-section of the parabola). If the focal length is 45 meters, find the depth of the dish, rounded to one decimal place.
     ::卫星天线的视线形状直径为80米。收集的电视信号集中在一个点上,称为“焦点”点,这是抛物体(抛物线的横截面)的焦点。如果焦距为45米,请找到天线的深度,四舍五入到小数点后一位。
  播放段落
  8. When new highways go in, they are often designed with parabolic surfaces which allow water to drain off. A new highway is being laid, it is 32 feet wide and is .4 feet higher in the center of the highway then on the sides. a) Find an equation if the parabola that models the highway surface (assume that the origin is at the center of the highway) b) How far from the center of the highway is the surface of the road .1 feet lower than in the middle?
     ::当新高速公路进入时,它们往往设计成抛物线表面,允许水排出。一个新的高速公路正在铺设,宽32英尺,在高速公路中心高4英尺,然后在两侧。 (a) 如果模拟高速公路表面的抛物线(假定原地在高速公路中心)找到一个方程(b) 公路中心离公路中心有多远,公路表面比中间低1英尺?
  播放段落
  9. The internal distance of the sketch of an arch is 8cm and the height of the arch is 9cm. Assuming the scale 1cm = 2m, work out a formula which calculates the actual height of the inside edge of this structure , in meters at any horizontal distance x measured from the origin point which is the floor at the center of the arch.
     ::拱门的草图内部距离为8厘米,拱门的高度为9厘米。假设比例为1厘米=2米,请设计一个公式来计算这个结构内边缘的实际高度,以从拱门中心底部的起点测量的任何水平距离x计的米计。

  播放段落

  A new bridge has been built for foot traffic cross a river. The two towers on either end of the bridge are 50 feet high and 300 feet away from each other. The supporting cables (2) are connected at the top of the towers and hang in a curve that forms the shape of a parabola. There are vertical cables that connect the walkway to the supporting cables. These cables connect every 15 feet from the walkway up to the supporting cables. At the center of the bridge, the parabola is 5 feet above the walkway.
  ::修建了一条新的桥梁,供徒步穿越河流,桥两端的两座塔座高50英尺,彼此相距300英尺。辅助电缆(2)连接在塔顶,挂在形成抛物线形状的曲线上。有垂直电缆连接着行道与支撑电缆。这些电缆连接着从行道到支撑电缆的每15英尺。在桥中心,抛物线位于行道上方5英尺处。

  播放段落

  Specialty Cable Company back east sells cable for $52.75 per 10 feet with a shipping charge of $300.00 for the entire order. Cables R US, on the West Coast sells cable for $432.90 per 100 feet with a shipping charge of $350.00 for the entire order. Cable had to be purchased in either 10-foot lengths from SCC or in 100-foot lengths from CRUS. Once purchased, the cables can be cut or welded together.
  ::东面的特种电缆公司出售电缆每10英尺52.75美元,整个订单的运费为300.00美元,西海岸的R公司出售电缆每100英尺432.90美元,整个订单的运费为350.00美元,从SCC以10英尺长或从CRUS以100英尺长购买电缆,一旦购买,电缆可以一起切割或焊接。

  播放段落
  10. Write an equation for the parabola that represents each of the support cables.
      ::为代表每个支持电缆的抛物线写一个方程。
  播放段落
  11. Determine the number of vertical cables needed.
      ::确定所需纵向电缆的数量。
  播放段落
  12. Determine the length of each of the vertical cables.
      ::确定每条垂直电缆的长度。
  播放段落
  13. How much does it cost to purchase the needed materials from each company?
      ::从每家公司购买所需材料要花多少钱?

  播放段落

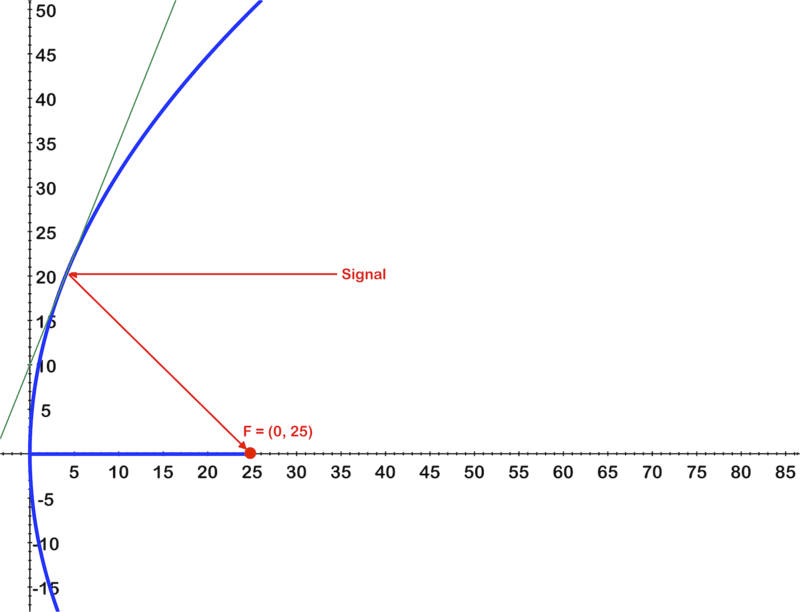
  Look at the image. It shows the parabolic cross section of a satellite dish antenna. The equation for the parabola is $\begin{align*}x = 0.01y^2\end{align*}$
  ::查看图像。 它显示卫星天线的抛光横截面段。 抛光线的方程式是 x= 0.01y2

  播放段落
  14. A radio signal comes in at y = 20 as marked in red. Identify where the ray strikes the parabola, give coordinates.
      ::y = 20 红色标记的无线电信号进入 y = 20 。 确定射线击中抛物线的位置, 给坐标 。
  播放段落
  15. Identify the angle measure between the incoming ray and a line between the strike point and the focus.
      ::辨明射线与攻击点和焦点之间的角度量。
  播放段落
  16. An incoming ray and its reflected ray make angles of equal measure with a line tangent to the curved surface. Use the angle you just measured between the signal and the reflected line to calculate the measures of the angles between the incoming signal and the tangent to the point of impact and from the tangent to the reflected ray. Are they the same? Measure with a protractor to confirm your calculations.
      ::射入的射线及其反射射线将等量角度与曲线表面的直线相切。使用刚刚测量的信号和反射线之间的角来计算射入的信号和正切到撞击点之间的角,以及从正切到反射线之间的角的度量。它们是否相同?用一个减序测量器来确认您的计算结果。
  播放段落
  17. Find the equation for the tangent line. Use angle C to find its slope.
      ::查找正切线的方程。 使用角度 C 查找其斜度 。
  播放段落
  18. Randomly choose another incoming ray. Calculate the angles as before. Is the incoming ray tangent to the parabola at the point where the incoming ray strikes the graph? How do you know?
      ::随机选择另一个输入的射线。 与过去一样计算角度。 输入的射线正切到抛物线是否在射入的射线击中图点? 你怎么知道 ?
  播放段落
  19. What can you say about the direction a reflected ray takes whenever the incoming ray is parallel to the axis of the parabola? Can you see why the name "focus" is used and why television satellite antennas and other listening devices are made in the shape of a paraboloid?
      ::当射线与抛物线轴平行时,反射线取向的方向如何?你能理解为什么使用“焦距”这个名称,为什么电视卫星天线和其他监听装置以抛物体的形式制作?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

   

  播放段落

  Resources
  ::资源