6.6 超重波赤道和联系财产

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节超双波赤道和协调人财产

  折叠 展开

  超双波赤道和协调人财产

  播放段落

  Adrian and Evan were discussing the math class they just completed. The class focused on (pun intended!), and reviewed the properties of hyperbolas.
  ::Adrian和Evan正在讨论他们刚刚完成的数学课程。 课程侧重于( pun 想要的! ) , 并审查了双曲线的特性 。

  播放段落

  Adrian thinks that hyperbolas are very similar to the that they studied last week, and believes that the shapes are really the same. Evan thinks that it does not matter what the parts of the hyperbola look like, since it is the complete shape that they are studying.
  ::亚德里安认为超光球和他们上星期研究的非常相似,并且认为形状完全一样。 埃文认为超光波拉的部分长什么样并不重要,因为它是他们正在研究的完整形状。

  播放段落

  Who is correct?
  ::谁是正确的?

  播放段落

  Hyperbola Equations and the Focal Property
  ::超双波赤道和协调人财产

  播放段落

  Compared to parabolas and , hyperbolas may seem... messy! Not only is it an infinite shape, but there are two pieces that aren’t even connected! Hyperbolas are though: when the plane slices through two parts of the cone, the two infinite “U”-shaped parts are together called a hyperbola .
  ::与Parabolas和Parabolas相比, 超大陈列物可能看起来... ...... 混乱! 不仅它是一个无限的形状, 而且还有两个甚至没有连接的形状! 但是, 超大陈列物是: 当平面穿过锥壳的两个部位切开时, 两个无限的“ U”形的部件被放在一起, 被称为超大圆形。

  

  播放段落

  In this section we will see that this sprawling shape actually has some beautiful properties that make it as noble as its cousins.
  ::在本节中,我们将看到这种无孔不入的形状实际上有一些美丽的特性,使它与表兄弟一样高贵。

  播放段落

  The Focal Property
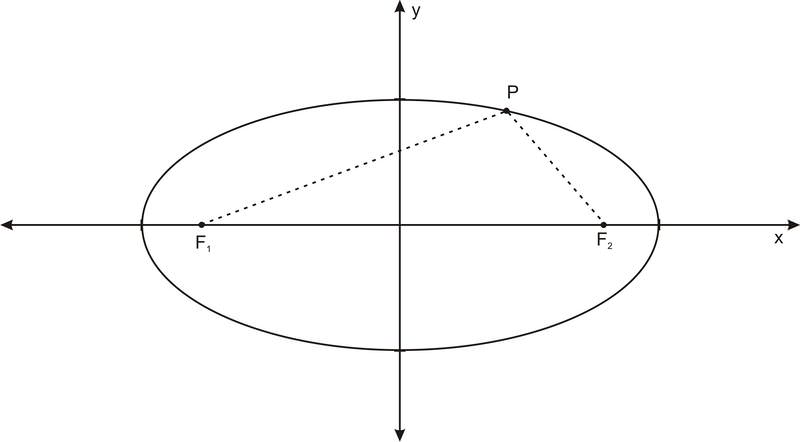
  ::协调人财产

  播放段落

  Even though this shape seems much harder to conceive of than an ellipse, the hyperbola has a defining focal property that is as simple as the ellipse’s. Remember, an ellipse has two foci and the shape can be defined as the set of points in a plane whose distances to these two foci have a fixed sum.
  ::尽管这种形状似乎比椭圆要难想象得多,但双曲线具有与椭圆一样简单的定义焦距属性。 记住,椭圆有两个面,形状可以定义为与这两个面的距离有固定数字的平面上的一组点。

  

  播放段落

  Hyperbolas also have two foci, and they can be defined as the set of points in a plane whose distances to these two points have the same difference . So in the picture below, for every point $\begin{array}{r}P\end{array}$ on the hyperbola, $\begin{array}{r}|d_2-d_1|=C\end{array}$ for some constant $\begin{array}{r}C\end{array}$ .
  ::Hyperbolas 也有两个角度, 它们可以定义为一个平面上的点数, 与这两个点的距离是相同的。 因此在下面的图画中, 超波拉上的每点P, 某些恒定的 C , @ d2 - d1 C 。

  

  播放段落

  The general form for a hyperbola that opens upwards and downwards and whose foci lie on the $\begin{array}{r}y-\end{array}$ axis is:
  ::向上和向下打开的双重波拉的一般形式,其基轴上的基质如下:

  播放段落

  $$\begin{array}{r}\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\end{array}$$

  
  ::y2a2 - x2b2=1

  播放段落

  Switching $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ we have hyperbolas that open rightwards and leftwards and whose foci lie on the $\begin{array}{r}x-\end{array}$ axis.
  ::切换 x 和 y,我们有超高球 向右开,向左开, 其角在 x - 轴上。

  播放段落

  $$\begin{array}{r}\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\end{array}$$

  
  ::x2a2-y2b2=1

  播放段落

  For a hyperbola that is centered around the point $\begin{array}{r}(h,k)\end{array}$ we have the shifted equations:
  ::对于围绕点(h,k)的超重波拉,我们有变式方程式:

  播放段落

  $$\begin{array}{r}\frac{(y-k{)}^2}{a^2}-\frac{(x-h{)}^2}{b^2}=1\end{array}$$

  
  :y-k)2a2-(x-h)2b2=1

  播放段落

  for a hyperbola opening up and down, and
  ::来来来去去去去的双重波拉,

  播放段落

  $$\begin{array}{r}\frac{(x-h{)}^2}{a^2}-\frac{(y-k{)}^2}{b^2}=1\end{array}$$

  
  :x-h)2a2-(y-k)2b2=1

  播放段落

  for a hyperbola opening left and right.
  ::向左、右、向左打开的双倍波拉。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked whether Evan or Adrian is correct.
  ::之前有人问你是埃文还是阿德里安是对的

  播放段落

  Evan and Adrian are both correct in their own ways. Adrian is correct that a hyperbola is just two parabolas in opposite directions, which becomes clear when you consider that a parabola is created by slicing a single cone, and a hyperbola by slicing two identical cones at the same time. Evan is correct that although a hyperbola is constructed of two parabolas, it is the complete shape that they are studying, and many or most of the formulas and definitions that they will consider only apply to the complete shape.
  ::埃文和阿德里安两者的方式都是正确的。阿德里安正确地指出,双波拉只是两个相反方向的双波拉,当你认为一个抛物线是通过切开一个锥形而创造的,而一个双波拉是通过同时切开两个相同的锥形而创造的。 埃里凡是正确的,虽然一个超波拉是由两个抛物线组成的,但它是他们正在研究的完整形状,以及许多或大多数公式和定义,他们认为这些公式和定义将只适用于完整的形状。

  播放段落

  Example 2
  ::例2

  播放段落

  The hyperbola is infinite in size. In mathematics this is called unbounded , which means no circle , no matter how large, can enclose the shape. Explain why a focal property involving a difference results in an unbounded shape, while a focal property involving a sum results in a bounded shape.
  ::双曲线的大小是无限的。 在数学中, 它被称为无约束的, 这意味着没有圆, 不论大小, 都无法附加形状 。 解释一个包含差异的焦点属性为什么导致一个未约束的形状, 而一个包含一个总和的焦点属性则导致一个捆绑的形状 。

  播放段落

  In the case of an ellipse, we had two distances summing to a constant. Since the distances are both positive then there is a limit to the size of the numbers. In the case of hyperbolas, two very large positive numbers can have a much smaller difference, infinitely small in fact.
  ::以椭圆为例,我们有两段距离向恒定点的间距。由于距离都是正数,因此数字的大小有一定的限度。 在超光层中,两个非常大的正数可以有小得多的差别,事实上是很小的。

  播放段落

  Example 3
  ::例3

  播放段落

  Show that the following equation is a hyperbola. Graph it, and show its foci.
  ::显示以下方程式是一个双倍方程。 图形显示它, 并显示它的角 。

  播放段落

  $$\begin{array}{r}144x^2-576x-25y^2-150y-3249=0\end{array}$$

  
  ::144x2-576x-25y2-150y-3249=0

  播放段落

  The positive leading coefficient for the $\begin{array}{r}{x}^2\end{array}$ term and the negative leading coefficient for the $\begin{array}{r}{y}^2\end{array}$ term indicate that this is a hyperbola that is horizontally oriented. Grouping and completing the square, we have:
  ::x2 术语的正主要系数和 y2 术语的负主要系数表明,这是一个横向方向的双曲线。

  播放段落

  $$\begin{array}{rl}144(x^2-4x)-25(y^2+6y)& =3249\\ 144(x^2-4x+4)-25(y^2+6y+9)& =3249+576-225\\ 144(x-2{)}^2-25(y+3{)}^2& =3600\\ \frac{(x-2{)}^2}{5^2}-\frac{(y+3{)}^2}{{12}^2}& =1\end{array}$$

  
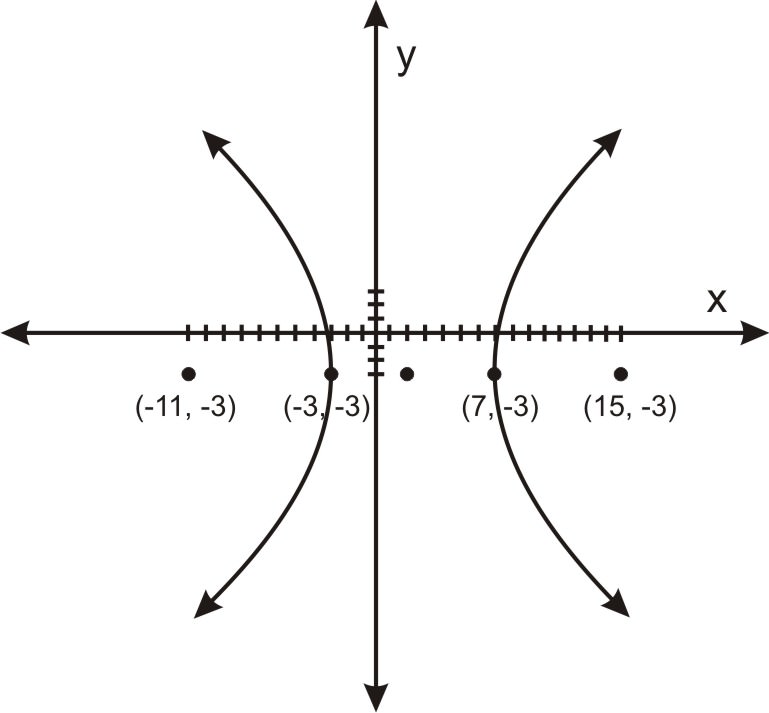
  ::144(x2-4x)-25(y2+6y)=3249144(x2-4x+4)-25(y2+6y+9)=3249+576-225144(x-2)2-25(y+3)2=3600(x-2)252-(y+3)22=1

  播放段落

  So our hyperbola is centered at (2,-3). Its vertices are 5 units to the right and left of (2,-3), or at the points (7,-3) and (-3,-3). It opens to the right and left from these vertices. It’s foci are $\begin{array}{r}c\end{array}$ units to the left and right of (2,-3), where $\begin{array}{r}c=\sqrt{a^2+b^2}=\sqrt{5^2+{12}^2}=13\end{array}$ . So it’s foci are at (15,-3) and (-11,-3). Plotting a few points near (7,-3) and (-3,-3), the graph looks like:
  ::因此,我们的双波拉以(2,3)为中心。它的脊椎向右和左5个单位(2,3)或点(7,3)和(3,3),从这些脊椎向右和左开放。它的脊椎向左和向左开放。它的脊椎向左和向右和向左是c 单位(2,3),C=a2+b2=52+122=13。它的脊椎在(15,3)和(11,3)之间。在靠近(7,3)和(3,3)处绘制几个点,图表看上去像:

  

  播放段落

  Example 4
  ::例4

  播放段落

  Graph the following hyperbola and mark its foci: $\begin{array}{r}16x^2+64x-9y^2+90y-305=0\end{array}$ .
  ::图如下双波拉,并标注其角:16x2+64x-9y2+90y-305=0。

  播放段落

  The positive leading coefficient for the term and the negative leading coefficient for the term indicate that this is a hyperbola that is horizontally oriented. Grouping and completing the square, we have:
  ::该术语的正主要系数和负主要系数表明,这是一个面向横向的双曲线。

  播放段落

  $\begin{array}{r}16(x^2+4x+4)-9(y^2-10y+25)-305=64-225\end{array}$
  ::16(x2+4x+4)-9(y2-10y+25)-305=64-225

  播放段落

  Factoring and combining like terms:
  ::保理和合并类似术语:

  播放段落

  $\begin{array}{r}16(x+2{)}^2-9(y-5{)}^2=144\end{array}$
  ::16(x+2)2-9(y-5)2=144

  播放段落

  Divide both sides by 144 and rewrite 9 and 16 as 3 ² and 4 ² :
  ::将双方除以144,并改写9和16为32和42:

  播放段落

  $\begin{array}{r}\frac{(x+2{)}^2}{3^2}-\frac{(y-5{)}^2}{4^2}=1\end{array}$
  :x+2)232-(y-5)242=1

  

  播放段落

  Example 5
  ::例5

  播放段落

  Graph the following hyperbola and mark its foci: $\begin{array}{r}{x}^2-8x-y^2-4y=-28\end{array}$ .
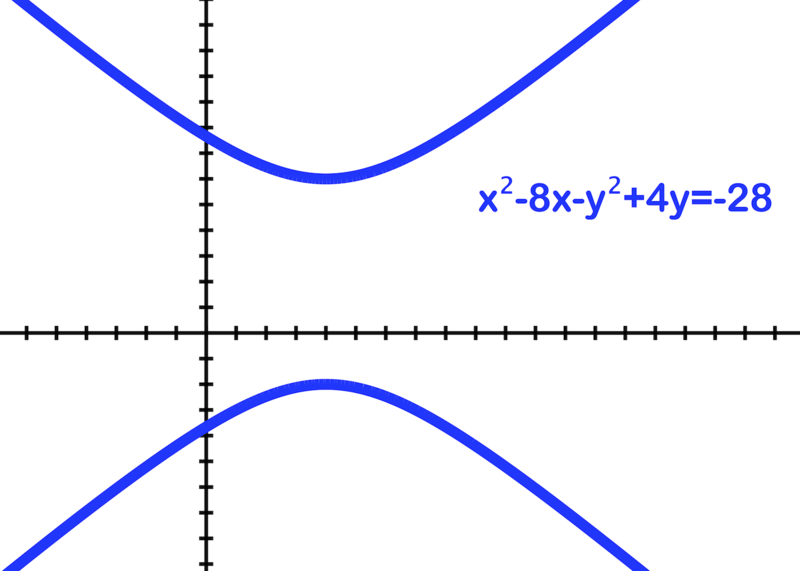
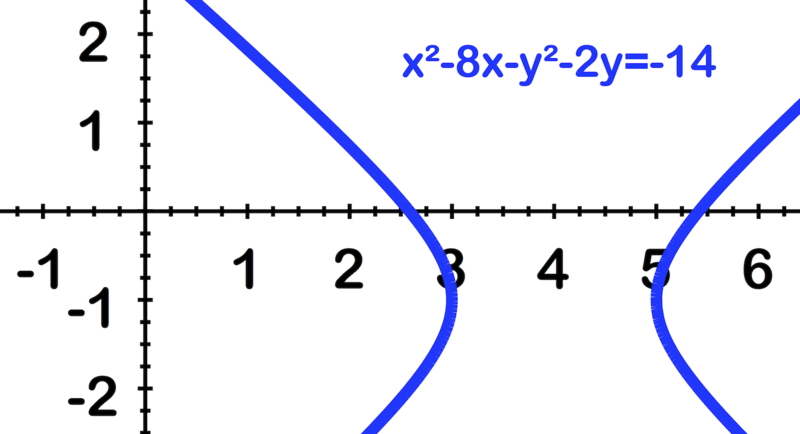
  ::图如下双波拉,并标注其角: x2-8x-y2-4y28。

  播放段落

  To graph $\begin{array}{r}{x}^2-8x-y^2+4y=-28\end{array}$ :
  ::图x2-8x-y2+4y28:

  播放段落

  $\begin{array}{r}(x-4{)}^2-(y-2{)}^2=-16\end{array}$ ..... complete the square to factor
  :x-4)2-2-(y-2)2 16.... 将正方形乘以系数

  播放段落

  $\begin{array}{r}\frac{(y-2{)}^2}{16}-\frac{(x-4{)}^2}{16}=1\end{array}$ ..... rewrite in standard form
  :y-2)216-(x-4)216=1 ....以标准格式重写

  播放段落

  $\begin{array}{r}x-4=0\to x=4\end{array}$ and $\begin{array}{r}y-2=0\to y=2\end{array}$ ..... therefore the center is (4, 2)
  ::x-4=0x=4和y-2=0y=2...。 因此中心是 (4, 2)

  播放段落

  Mark 4 units left and right of (4, 2) and Mark 2 units above and below (4, 2), use those four points to define the sides of a box.
  ::标记4个单位的左侧和右侧(4,2)和2个单位的左侧和右侧(4,2)和2个单位的马克(4,2),使用这4个点来界定一个盒子的侧面。

  播放段落

  Connect the corners of the box to illustrate the asymptotes.
  ::连接框的角以显示小数点 。

  播放段落

  Since the "y" term is the positive one, the hyperbola opens up and down.
  ::因为“y”一词是积极的, 超大波拉是上下打开的。

  播放段落

  Graph the hyperbola, it should look like this:
  ::图形显示双波拉, 它应该看起来像这个 :

  

  播放段落

  Example 6
  ::例6

  播放段落

  Graph the following hyperbola: $\begin{array}{r}{x}^2-8x-y^2-2y=-14\end{array}$ .
  ::如下双倍波拉图: x2-8x-y2-2-2y14。

  播放段落

  To graph $\begin{array}{r}{x}^2-8x-y^2-2y=-14\end{array}$ :
  ::图x2-8x-y2-2y_2y14:

  播放段落

  $\begin{array}{r}(x-4{)}^2-(y+1{)}^2=1\end{array}$ ..... complete the square to factor $\begin{array}{r}\frac{(x-4{)}^2}{1}-\frac{(y+1{)}^2}{1}=1\end{array}$ ..... rewrite in standard form
  :- 4) 2 - (y+1) 2=1 .... 将正方形填充为系数( x-4) 21 - (y+1) 21= 1 。 重写为标准格式 。

  播放段落

  $\begin{array}{r}x-4=0\to x=4\end{array}$ and $\begin{array}{r}y+1=0\to y=-1\end{array}$ ..... therefore the center is (4, -1)
  ::x4=0x=4和y+1=0y1...。 因此中心是 (4, -1)

  播放段落

  Mark 4 units left and right of (4, -1) and Mark 1 unit above and below (4, -1), use those four points to define the sides of a box.
  ::标记4个单位的左侧和右侧(4,-1)和上下(4,-1)的标记1个单位(4,-1)使用这四个点来界定一个方框的侧面。

  播放段落

  Connect the corners of the box to illustrate the asymptotes.
  ::连接框的角以显示小数点 。

  播放段落

  Since the "x" term is the positive one, the hyperbola opens left and right.
  ::由于“x”一词是肯定的,超博拉向左和向右打开。

  播放段落

  Graph the hyperbola, it should look like this:
  ::图形显示双波拉, 它应该看起来像这个 :

  

  播放段落

  Example 7
  ::例7

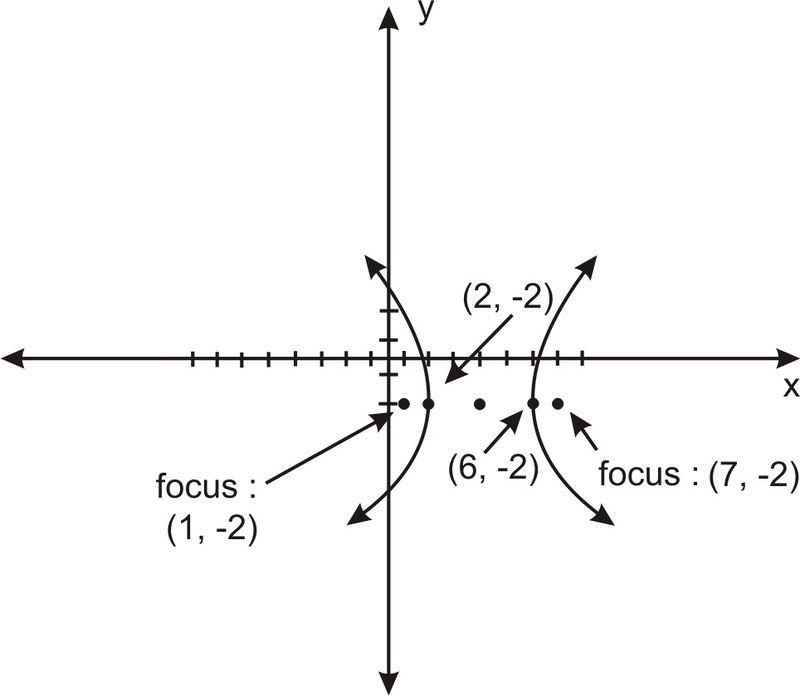
  播放段落

  Find the equation for the following hyperbola:
  ::查找以下双曲线的方程 :

  

  播放段落

  $\begin{array}{r}\frac{(x-4{)}^2}{4}-\frac{(y+2{)}^2}{45}=1\end{array}$
  :x-4)24-(y+2)24-245=1

  播放段落

  Review
  ::回顾

  播放段落

  Sketch the hyperbolas.
  ::涂抹超高音波

  播放段落
  1. $\begin{array}{r}\frac{(x+4{)}^2}{4}-\frac{(y-1{)}^2}{9}=1\end{array}$
     :x+4)24-(y-1)29=1
  播放段落
  2. $\begin{array}{r}\frac{(y+3{)}^2}{4}-\frac{(x-4{)}^2}{9}=1\end{array}$
     :y+3)24-(x-4)29=1
  播放段落
  3. $\begin{array}{r}\frac{(y+4{)}^2}{16}-\frac{(x-1{)}^2}{4}=1\end{array}$
     :y+4) 216-(x-1)24=1
  播放段落
  4. $\begin{array}{r}(x-2{)}^2-4y^2=16\end{array}$
     :x-2)2-2-4y2=16
  播放段落
  5. $\begin{array}{r}\frac{y^2}{4}-\frac{(x-1{)}^2}{4}=1\end{array}$
     ::y24 - (x- 1) 24= 1
  播放段落
  6. $\begin{array}{r}\frac{(x-2{)}^2}{16}-\frac{(y+4{)}^2}{1}=1\end{array}$
     :x-2)216-(y+4)21=1
  播放段落
  7. $\begin{array}{r}\frac{(x+2{)}^2}{9}-\frac{(y+2{)}^2}{16}=1\end{array}$
     :x+2)29-(y+2)216=1
  播放段落
  8. $\begin{array}{r}\frac{(x+4{)}^2}{9}-\frac{(y-2{)}^2}{4}=1\end{array}$
     :x+4)29-(y-2)24=1
  播放段落
  9. Graph the hyperbola and mark its foci: $\begin{array}{r}9y^2+18y-x^2+4x-4=0\end{array}$
     ::绘制双曲线图并标记其角值: 9y2+18y-x2+4x-4=0
  播放段落
  10. Graph the hyperbola and mark its foci: $\begin{array}{r}25x^2+150x-4y^2+24y+89=0\end{array}$
      ::绘制双曲线图,并标记其方轴: 25x2+150x-4y2+24y+89=0

  播放段落

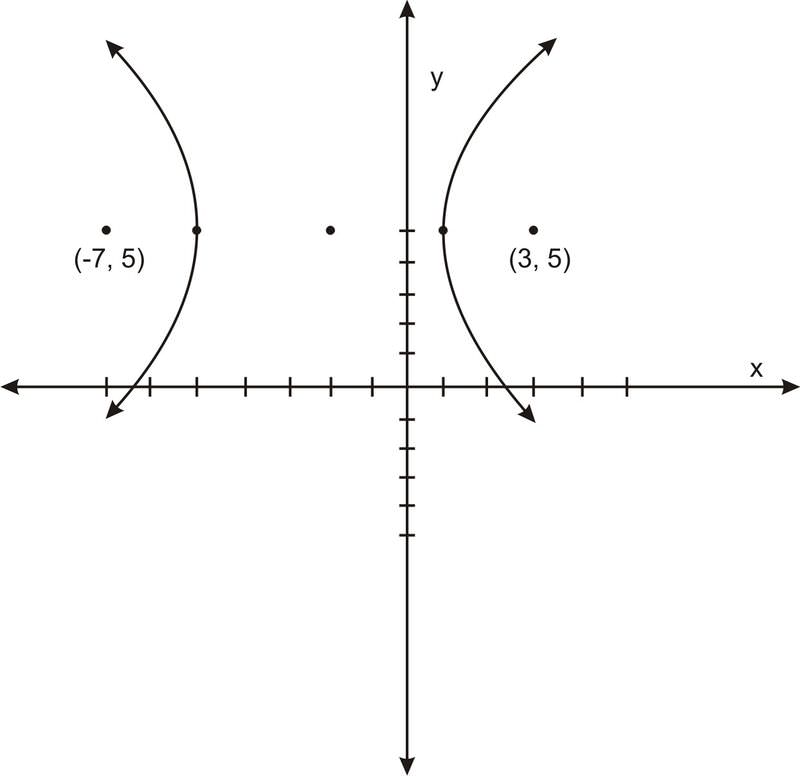
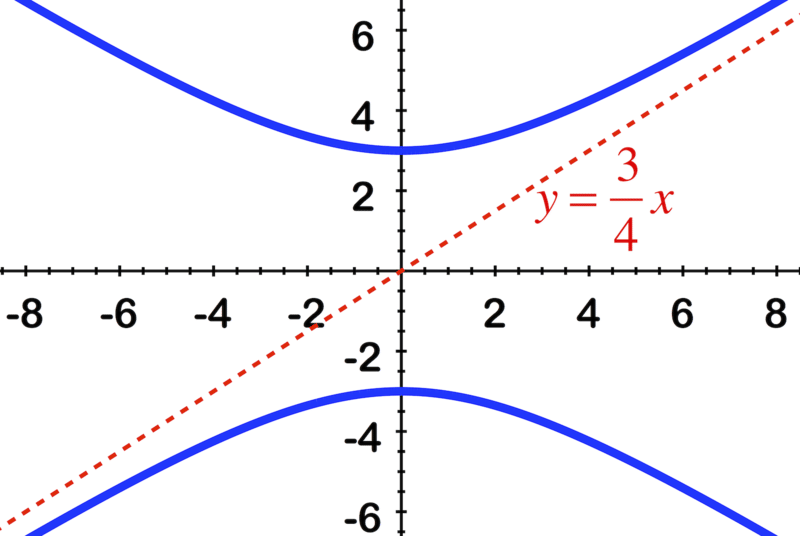
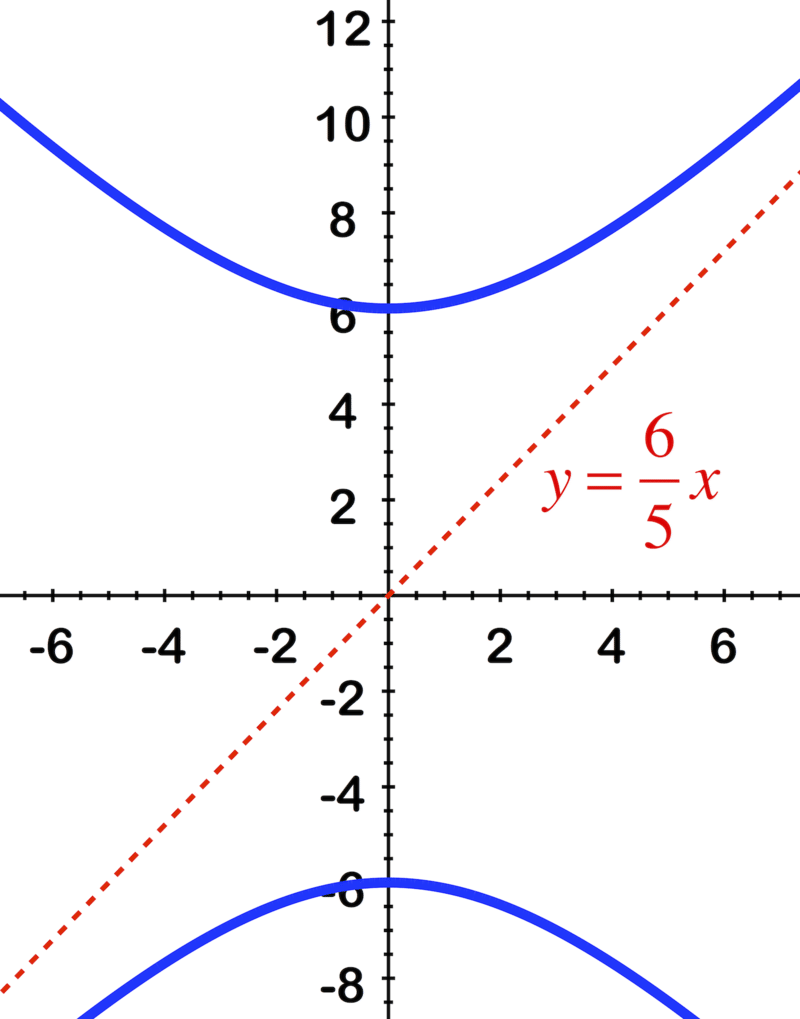
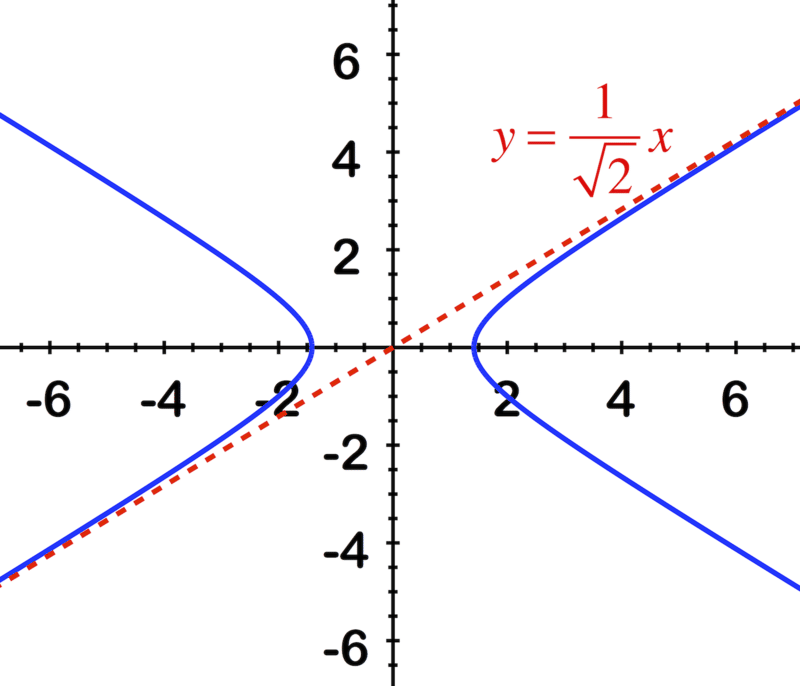
  Identify the equation of the hyperbola using the image.
  ::使用图像识别双倍波拉的方程式 。

  11. 
  12. 
  13. 
  14. 
  15. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。