8.3 无限限制
Section outline
-
Geeks-R-Us sells titanium mechanical pencils to computer algorithm designers. In an effort to attract more business, they decide to run a rather unusual promotion:
::Geeks-R-Us向计算机算法设计师出售钛机械铅笔。 为了吸引更多的生意,他们决定经营一个非常不寻常的促销:"SALE!! The more you buy, the more you save! Pencils are now $ 12 x x − 3 per dozen!"
::你买得越多,救得越多!If the tri llionaire, Spug Dense, comes in and says he wants to buy as many pencils as Geeks-R-Us can turn out, what will the cost of the pencils approach as the order gets bigger and bigger?
::如果万亿富翁Spug Dense 进来说 他想买多少铅笔 只要Geeks-R-Us能发现, 铅笔的成本会随着订单的越来越高而增加多少?Infinite Limits
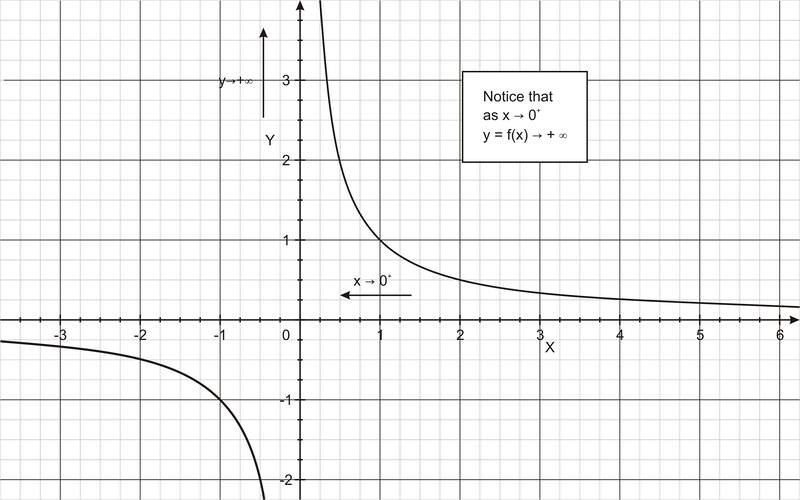
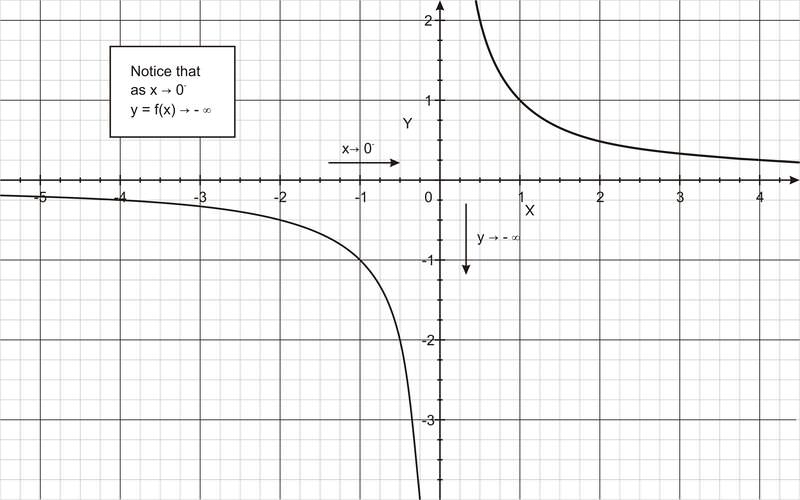
::无限限制Sometimes, a function may not be defined at a particular number, but as values are input closer and closer to the undefined number, a limit on the output may not exist. For example, for the function f ( x ) = 1/x (shown in the figures below), as x values are taken closer and closer to 0 from the right, the function increases indefinitely. Also, as x values are taken closer and closer to 0 from the left, the function decreases indefinitely.
::有时,函数可能无法在一个特定数字上定义,但由于数值是输入接近和接近未定义数字的输入,输出可能不存在限制。例如,对于函数 f(x) = 1/x(在下图中显示),当x 值从右侧接近和接近0 时,函数将无限期增加。此外,由于x 值从左侧接近和接近0,函数将无限期减少。We describe these limiting behaviors by writing
::我们用书面描述这些限制行为。lim x → 0 + 1 x = + ∞
::立方公尺x0+1xlim x → 0 − 1 x = − ∞
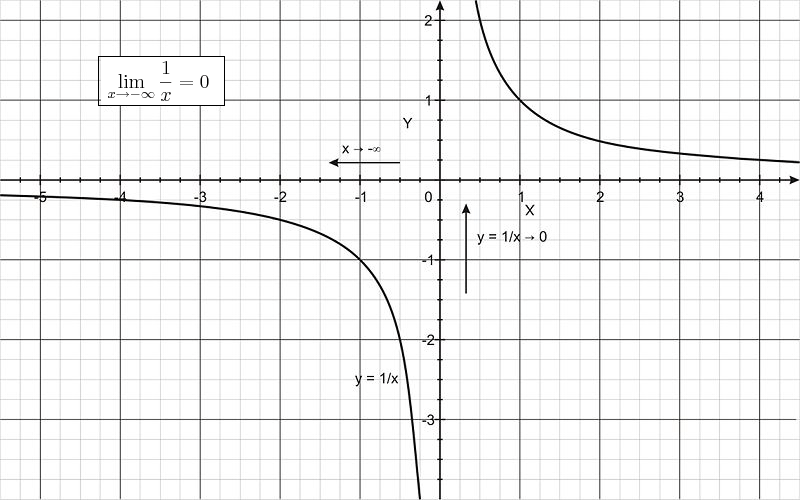
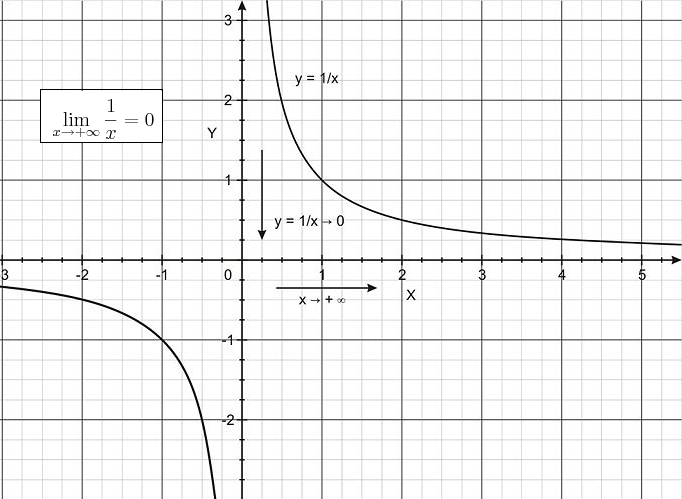
::立方公尺Sometimes we want to know the behavior of f ( x ) as x increases or decreases without bound. In this case we are interested in the end behavior of the function, a concept you have likely explored before. For example, what is the value of f ( x ) = 1/x as x increases or decreases without bound? That is,
::有时我们想要知道 f( x) 作为 x 递增或递减而不受约束的行为。 在此情况下, 我们对函数的最终行为感兴趣, 您以前可能已经探索过这个概念 。 例如, f( x) = 1/x 作为 x 递增或递减而不受约束的值是多少 ? 也就是说, f( x) = 1/x 作为 x 递增或递减是多少 ?lim x → + ∞ 1 x = ?
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?lim x → − ∞ 1 x = ?
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?As you can see from the graphs (shown below), as x decreases without bound, the values of f ( x ) = 1/x are negative and get closer and closer to 0. On the other hand, as x increases without bound, the values of f ( x ) = 1/x are positive and still get closer and closer to 0.
::从图表(如下表所示)可以看出,当x无约束地下降时,f(x)=1/x的值为负值,接近于0。另一方面,当x无约束地增加时,f(x)=1/x的值为正值,仍然接近于0。That is,
::也就是说,lim x → + ∞ 1 x = 0
::limx1x=0lim x → − ∞ 1 x = 0
::limx1x=0Examples
::实例Example 1
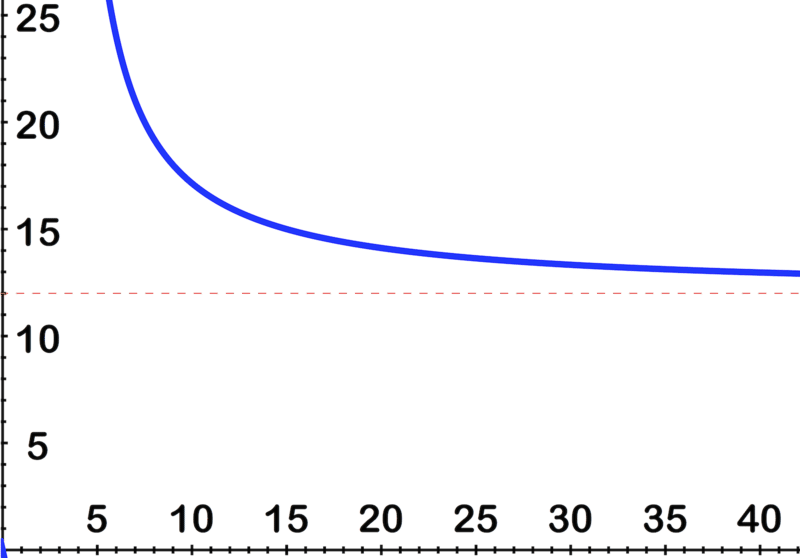
::例1Earlier, you were asked a question about buying a lot of pencils.
::之前有人问过你 买很多铅笔的问题As Spug buys more and more pencils, the cost of each dozen will drop quickly at first, and level out after a while, approaching $12 per dozen.
::斯普格购买的铅笔越来越多, 每12支铅笔的成本一开始会迅速下降, 过一阵子就会稳定下来, 接近每12美元12美元。You can see the effect on the graph here:
::您可以在此看到图中的效果 :Example 2
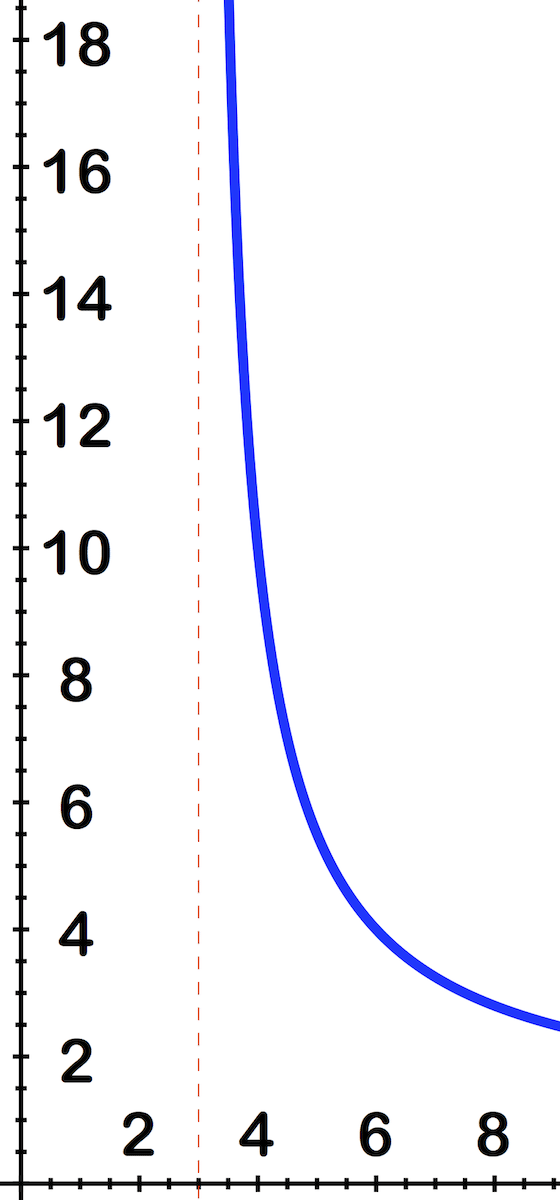
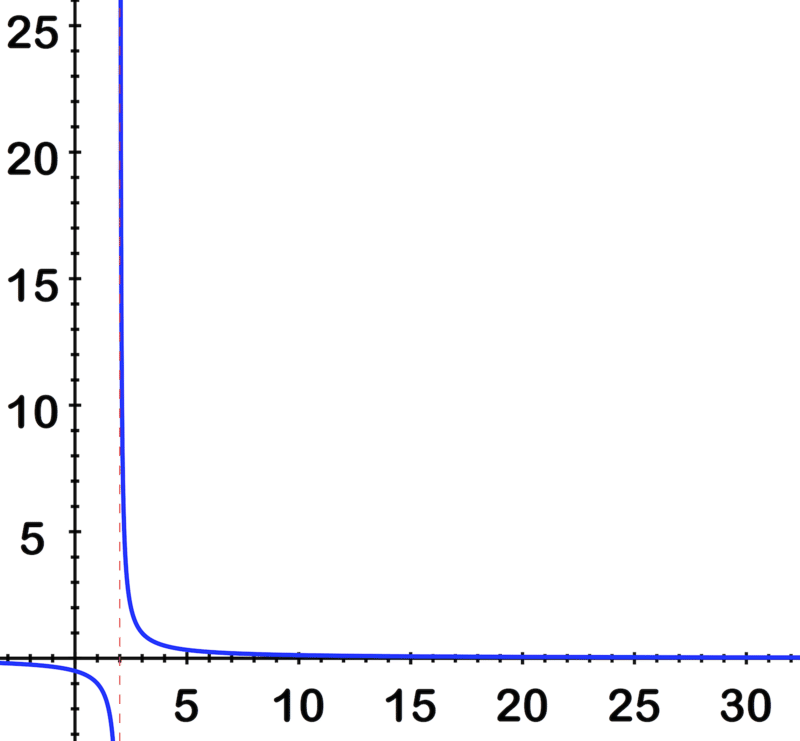
::例2Evaluate the limit by making a graph: lim x → 3 + x + 6 x − 3 .
::通过绘制一个图: limx3+x+6x-3, 来评估极限值 。By looking at the graph:
::通过查看图表:We can see that as x gets closer and closer to 3 from the positive side, the output increases right out the top of the image, on its way to ∞
::我们可以看到,当x从正面接近3时, 输出会从图像的顶部上升,Example 3
::例3Evaluate the limit: lim x → ∞ 11 x 3 − 14 x 2 + 8 x + 16 9 x − 3 .
::评估极限值: limx11x3- 14x2+8x+169x-3。To evaluate , a little bit of intuition helps. Let's think this one through.
::评估一下,直觉能帮上点忙。让我们好好想想这个。First, note that since we are looking at what happens as x → ∞ most of the interesting stuff will happen as x gets really big.
::首先,请注意,既然我们是在看什么 发生作为x 大部分有趣的事情 会发生 当x变得真正大。On the top part of the fraction, as x gets truly massive, the 11x 3 part will get bigger much faster than either of the other terms. In fact, it increases so much faster than the other terms completely cease to matter at all once x gets really monstrous. That means that the important part of the top of the fraction is just the 11x 3 .
::在分数的顶端, 当 x 变得真正巨大时, 11x3 部分会比其他两个条件中的任何一个大得多。 事实上, 它的增加比其他条件都快得多。 一旦 x 变得非常可怕, 它就会完全停止重要。 这意味着该分数顶部的重要部分只是 11x3 。On the bottom, a similar situation develops. As x gets really, really big, the -3 matters less and less. So the bottom may as well be just 9x .
::在底部, 类似的情况也会发展。 当 x 变大时, - 3 的值越来越小。 所以底部的值可能只有 9x 。That gives us 11 x 3 9 x which reduces to 11 x 2 9
::这让我们11x39x 减到11x29Now we can more easily see what happens at the "ends." As x gets bigger and bigger, the numerator continues to get bigger faster than the denominator, so the overall output also increases.
::现在,我们可以更容易地看到“端”会发生什么。随着 x 越来越大, 分子继续变得更快于分母, 所以总输出也会增加。∴ lim x → + ∞ 11 x 3 − 14 x 2 + 8 x + 16 9 x − 3 is + ∞
::============================================================================================================================================== ================================================================================================================================================================Example 4
::例4Evaluate lim x → 0 x + 2 x + 3 .
::评估 limx=0x+2x+3。This one is easier than it looks! As x --> 0, it disappears, leaving just the fraction: 2/3
::这个比看起来容易得多。 作为 x - > 0, 它会消失, 只留下分数: 2/3Example 5
::例5Make a graph to evaluate the limit lim x → ∞ 1 √ x and lim x → 0 + 1 √ x .
::绘制一个图表以评价 limx1x 和 limx0+1x 的限值 。By looking at the image, we see that as x gets huge, so does √ x which means that 1 is being divided by an ever-larger number, and the result is getting smaller and smaller.
::通过观察图像,我们可以看到,当x变大时,x值也变大,x值也变大,这意味着1值被一个越来越大的数字除以,结果越来越小。lim x → ∞ 1 √ x = 0
::1x=0On the same image, we can see that as x gets closer and closer to zero, so does √ x which means that 1 is being divided by an ever smaller number, and the result gets bigger and bigger.
::在同一图像上,我们可以看到,当x接近零时,x接近零时,“x”也接近零时,“x”也接近零时,这意味着1除以一个越来越小的数字,结果越来越大。lim x → 0 + 1 √ x is + ∞
::立方公尺======================================================================================================================================================================================================================Example 6
::例6Graph and evaluate the limit: lim x → 2 + 1 x − 2 .
::图表和评估极限: limx%2+1x-2。By looking at the image, we can see that as x gets closer and closer to 2 from the positive direction, 1 gets divided by smaller and smaller numbers, so the result gets larger and larger.
::通过观察图像,我们可以看到,当x从正向接近2时,1时除以较小数目,结果就会越来越大。
lim x → 2 + 1 x − 2 is + ∞
::limx% 2+1x-2 是 @ @ labelReview
::回顾Evaluate the limits:
::评估限度:-
lim
x
→
3
−
1
x
−
3
::立方厘米 3 - 1x - 3 -
lim
x
→
−
4
+
1
x
+
4
::limx4+1x+4 -
lim
x
→
−
(
8
3
)
+
1
3
x
+
8
::limx(83)+13x+8 -
lim
x
→
−
5
+
(
x
2
+
11
x
+
30
)
x
+
5
::limx5+(x2+11x+30x+30x+5) -
lim
x
→
−
∞
(
x
2
+
11
x
+
30
)
x
+
5
::limx(x2+11x+30x+30x+5) -
lim
x
→
∞
−
11
x
3
+
20
x
2
+
15
x
−
17
−
9
x
3
+
5
x
2
−
x
−
17
::立方公尺xxx3+20x2+15x-7-9x3+5x2-x-17 -
lim
x
→
∞
13
::立方公尺13 -
lim
x
→
∞
−
2
x
+
18
17
x
−
3
::limx% 2x+1817x- 3 -
lim
x
→
∞
15
::limx% 15 -
lim
x
→
∞
−
5
x
2
+
5
x
+
14
::limx=%5x2+5x+14 -
lim
x
→
∞
7
x
+
12
::limx=% 7x+12 -
lim
x
→
∞
−
3
x
+
13
::limx=%3x+13 -
lim
x
→
∞
13
x
−
8
19
x
3
−
11
x
2
+
x
+
4
::立方公尺13x-819x3-11x2+x+4 -
lim
x
→
∞
−
17
x
+
14
::limx17x+14 -
lim
x
→
∞
−
7
x
2
−
2
x
−
13
::立方 7x2 - 2x - 13
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
lim
x
→
3
−
1
x
−
3