Course: 6.5 相互包容的活动 -- -- 概率和统计 | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 相互包容的活动 -- -- 概率和统计

Collapse Expand
相互包容的活动 -- -- 概率和统计
How does the for the union of probabilities: $\begin{aligned} P (A o r B) = P (A) + P (B) \end{aligned}$ work when at least some of the events overlap? For example, in a room with 20 people, there are 5 women wearing red and 5 wearing yellow, and there are 5 men wearing red and 5 wearing green. What is the probability of randomly picking one person who is either wearing red or is a man?
::概率联盟:P( A) 或 B( B) = P( A) + P( B) 如何在至少某些事件重叠时工作? 例如,在20人所在的房间里,有5名妇女穿红色,5名妇女穿黄色,5名男子穿红色,5名男子穿绿色。随机挑选一个要么穿红,要么是男子的人的概率是多少?

Since $\begin{aligned} P (w e a r i n g r e d) \end{aligned}$ actually overlaps with $\begin{aligned} P (m a n) \end{aligned}$ , we can’t just use the addition rule, so how do we find the answer?
::因为P(穿红色)实际上与P(man)重叠, 我们不能只使用附加规则, 我们如何找到答案?

We will return to this question at the end of the lesson.
::我们将在教训结束时再谈这个问题。

Mutually Inclusive Events
::相互包容的活动

Mutually in clusive events are events that have at least some amount of “overlap”, in other words, at least one of the favorable outcomes of one event is the same as a favorable outcome of another event. Because one or more outcomes may satisfy multiple cases, we cannot simply add up the probabilities as we did with mutually ex clusive events or we would end up with some events being counted twice. To account for the duplication, we just need to subtract the duplicated probabilities from the sum.
::相互包容的事件是至少具有一定数量的“重叠”事件,换句话说,至少一个事件的有利结果之一与另一个事件的有利结果相同。由于一个或一个以上的结果可能满足多个案例,我们不能简单地将概率和我们对相互排斥事件所做的一样相加,或者我们最终会把一些事件计算两次。为了说明重复,我们只需要从总数中减去重复的概率。

The modified formula looks like this:
::修改后的公式看起来是这样的:

$\begin{aligned} P (A o r B) (m u t u a l l y i n c l u s i v e) & = P (A) + P (B) - P (A a n d B) \\ Prob that either A or B will occur & = Prob of A occurring + Prob of B occurring - Prob of both at once \end{aligned}$

::P(A或B)(相互包容)=P(A)+P(B)-P(A)-P(B)-(A和B)

Calculating Probability
::计算概率

Consider a bag with five marbles in it. If there are three large marbles, one green, one blue, and one red, and also one each small red and small blue marbles, what is the probability that a random choice would be small or red?
::想象一个包里装有五大理石的袋子。如果有三大大理石,一个绿色,一个蓝色,一个红色,一个红色,还有一个每个小红和小蓝色大理石,那么随机选择是小的还是红的概率是多少?

If we were to try to solve this with the simple addition rule, we would wrongly get $\begin{aligned} \frac{2}{5} + \frac{2}{5} = \frac{4}{5} \end{aligned}$ or 80%.
::如果我们试图用简单的附加规则解决这个问题, 我们就会错误地得到25+25=45 或80%。

In fact, if we check that answer with a table of possible outcomes, we can see that it is incorrect since there are only three marbles that could qualify as either small or red: 1) The large red marble, 2) The small red marble, and 3) The small blue marble.
::事实上,如果我们用一个可能的结果表来核对答案,我们可以看到,这是不正确的,因为只有三种大理石可以称为小的或红的:1)大红大理石,2)小红大理石,3)小蓝色大理石。

The correct solution is:
::正确的解决办法是:

$\begin{aligned} \frac{1 large red + 2 small}{5 total marbles} = \frac{3}{5} o r 60 % \end{aligned}$

::1个大红+2小5个大红+2大圆球共计35个或60%

What went wrong when we used the simple addition rule? The problem is that we ended up counting the small red marble twice .
::当我们使用简单的附加规则时出了什么问题?问题在于我们最后两次数了红大理石的两次。

Incorrectly calculated: $\begin{aligned} \frac{(1 large red + 1 small red) + (1 small blue + 1 small red)}{5 total marbles} = \frac{4 m a r b l e s}{5 m a r b l e s} \end{aligned}$
::不正确计算1个大红+1小红)+(1个小蓝+1小红)5 总计大理石=4大理石5大理石

Properly calculated: $\begin{aligned} \frac{((1 large red + 1 small red) + (1 small blue)}{5 total marbles} = \frac{3 m a r b l e s}{5 m a r b l e s} \end{aligned}$
::正确计算(1个大红+1小红)+(1个小蓝色)5 总计大理石=3大理石5大理石

This leads us back to the modified addition rule for mutually inclusive events:
::这使我们又回到了经过修改的相互包容活动补充规则:

$\begin{aligned} P (A o r B) = (P (A) + P (B) - P (A a n d B)) \end{aligned}$

::P(A或B)=(P(A)+P(B)-P(A和B))

Calculating Theoretical Probability
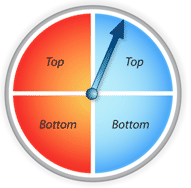
::计算理论概率

Suppose you are playing with the spinner in the image below. What is the theoretical probability that the spinner would randomly land on either a top quadrant or a red quadrant?
::假设您正在玩下方图像中的旋转器。旋转器随机降落在顶部象限或红色象限的理论概率是多少?

There are two favorable events here, red and top. To apply the modified addition rule, we need to know the probability of each case, and the probability of the intersection of the two cases:
::这里有两个有利的事件, 红色和顶部。要应用修改后的附加规则, 我们需要知道每个案例的概率, 以及两个案例的交叉概率 :

The probability of the spinner landing on red is:
::旋转器在红色上着陆的概率是:

$\begin{aligned} P (r e d) = \frac{2 red spaces}{4 total spaces} = \frac{1}{2} o r 50 % \end{aligned}$

::P(red)=2 红色空间4 总共空间=12或50%

The probability of the spinner landing on a top space is:
::旋转器在顶层空间着陆的概率是 :

$\begin{aligned} P (t o p) = \frac{2 top spaces}{4 total spaces} = \frac{1}{2} o r 50 % \end{aligned}$

::P( 上) = 2 顶空 4 总空数= 12 或 50%

The probability of the spinner landing on a top red space is:
::旋转器降落在顶层红色空间的概率是:

$\begin{aligned} P (t o p A N D r e d) = \frac{1 top red space}{4 total spaces} = \frac{1}{4} o r 25 % \end{aligned}$

::P( 上方和红色) = 1 顶层红色空间 4 总空域= 14 或25%

Inserting those values into the formula, we get:
::在公式中插入这些值后,我们得到:

$\begin{aligned} P (t o p O R r e d) = (\frac{1}{2} + \frac{1}{2}) - \frac{1}{4} = \frac{3}{4} o r 75 % \end{aligned}$

::P(最高或红色)=(12+12)-14=34=34或75%

Determining Inclusivity and Exclusivity
::确定包容性和包容性

If $\begin{aligned} P (A) = 40 % \end{aligned}$ , $\begin{aligned} P (B) = 30 % \end{aligned}$ , and $\begin{aligned} P (A a n d B) = 2 % \end{aligned}$ , are $\begin{aligned} P (A) \end{aligned}$ and $\begin{aligned} P (B) \end{aligned}$ mutually inclusive or mutually exclusive ?
::如果P(A)=40%,P(B)=30%,P(A和B)=2%,P(A)和P(B)是相互包容还是相互排斥?

This one is easier than it looks. If $\begin{aligned} P (A a n d B) \end{aligned}$ is greater than 0%, then they are inclusive, since it is possible for there to be outcomes that are both $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ .
::如果P( A) 和 B( B) 大于 0%, 那么它们就包含在内, 因为结果既可以是 A,也可以是 B 。

Earlier Problem Revisited
::重审先前的问题

In a room with 20 people, there are 5 women wearing red and 5 wearing yellow, and there are 5 men wearing red and 5 wearing green. What is the probability of randomly picking one person who is either wearing red or is a man?
::在一个有20人的房间里,有5名妇女穿红色,5名妇女穿黄色,5名男子穿红色,5名男子穿绿色。随机挑选一个要么穿红色,要么是男子的人的概率是多少?

Now we know to use the modified addition rule for inclusive events to solve this sort of problem:
::现在,我们知道使用经过修改的包容性事件附加规则来解决这类问题:

$\begin{aligned} P (r e d) & = \frac{5 women in red + 5 men in red}{20 total people} = \frac{1}{2} o r 50 % \\ P (m a l e) & = \frac{5 men in green + 5 men in red}{20 total people} = \frac{1}{2} o r 50 % \\ P (r e d, m a l e) & = \frac{5 men in red}{20 total people} = \frac{1}{4} o r 25 % \end{aligned}$

::P(red)=5 红色+5男子中的5名妇女,红色20人共=12人或50%P(男性)=5男子,绿色+5男子红色20人共=12人或50%P(红色,男性)=5男子,红色20人共=14人或25%

Therefore:
::因此:

$\begin{aligned} P (r e d \cup m a n) = \frac{1}{2} + \frac{1}{2} - \frac{1}{4} = \frac{3}{4} o r 75 % \end{aligned}$

::P(red man)=12+12-14=34或75%

Examples
::实例

Suppose you have a bag containing 5 quarters, 3 dimes, 4 nickels, 4 pennies, and 5 gold $1 coins.
::假设你有一个袋子内含5/4美元 3分 4分 4便士 4便士 5金1美元硬币

Example 1
::例1

1. What is the probability that a random coin will be either silver or worth less than 10 cents?
::1. 随机硬币是银币或价值低于10美分的概率有多大?

Use the modified addition rule for inclusive events:
::对包容性活动使用修改后的附加规则:

$\begin{aligned} P (A o r B) & = (P (A) + P (B) - P (A a n d B)) \\ P (s i l v e r o r < 10 c e n t s) & = (P (s i l v e r) + P (< 10 c e n t s) - P (s i l v e r a n d < 10 c e n t s)) \\ = (\frac{12}{21} + \frac{8}{21} - \frac{4}{21}) \\ P (s i l v e r o r < 10 c e n t s) & = \frac{16}{21} o r 76.2 % \end{aligned}$

::P(A 或 B) = (P(A) +P(B) +P(B) - P(A) - P(B) ) P(Silver 或 < 10美分) = (P(silver) +P( < 10美分) - P(silver 和 < 10美分) = (1221+821- 421) P(silver 或 < 10美分)=1621 或76.2%

Example 2
::例2

2. What is the probability that a random coin will be either gold or worth more than 10 cents?
::2. 随机硬币是黄金或价值超过10美分的概率有多大?

$\begin{aligned} P (g o l d o r > 10 c e n t s) & = (P (g o l d) + P (> 10 c e n t s) - P (g o l d a n d > 10 c e n t s)) \\ = (\frac{5}{21} + \frac{10}{21} - \frac{5}{21}) \\ P (g o l d o r > 10 c e n t s) & = \frac{10}{21} o r 47.6 % \end{aligned}$

::P(黄金或>10美分)=(P(黄金)+P(>10美分)-P(黄金和>10美分)=(521+1021-521)P(黄金或>10美分)=1021或47.6%

Example 3
::例3

3. What is the probability that you pick two coins in a row that are each either silver or worth more than 10 cents?
::3. 你每行挑两枚银币或价值超过10美分的硬币的概率是多少?

This is a two-step problem, first we need to calculate the probability of a single choice being silver or worth more than 10 cents, and then we can apply the to calculate the total probability.
::这是一个两步问题, 首先我们需要计算一个选择是银或价值超过10美分的概率, 然后我们就可以应用这个来计算总概率。

$\begin{aligned} P (s i l v e r o r > 10 c e n t s) & = (P (s i l v e r) + P (> 10 c e n t s) - P (s i l v e r a n d > 10 c e n t s)) \\ = (\frac{12}{21} + \frac{10}{21} - \frac{5}{21}) \\ P (s i l v e r o r > 10 c e n t s) & = \frac{17}{21} o r 81 % \end{aligned}$

::P( 硅或> 10 美分) = (P( 硅) +P( > 10 美分) - P( (硅和 > 10 美分) = (1221+ 1021 - 521) P( 硅或 > 10 美分) = 1721 或 81%

Now we use the multiplication rule: $\begin{aligned} P (A t h e n B) = P (A) \times P (B) \end{aligned}$
::现在我们使用乘法规则:P(A)然后是B)=P(A)xP(B)

$\begin{aligned} P (s i l v e r o r > 10 c e n t s then s i l v e r o r > 10 c e n t s) & = 0.81 \times 0.81 = 0.656 \\ P (s i l v e r o r > 10 c e n t s then s i l v e r o r > 10 c e n t s) & = 66 % \end{aligned}$

::P(硅或>10美分,然后银或>10美分)=0.81x0.81=0.656P(硅或>10美分,然后银或>10美分)=66%

Example 4
::例4

4. What is the probability that a random coin is either worth more than 9 cents or silver?
::4. 随机硬币价值超过9美分或银的概率是多少?

$\begin{aligned} P (> 9 c e n t s o r s i l v e r) & = (P (> 9 c e n t s) + P (s i l v e r) - P (> 9 c e n t s a n d s i l v e r)) \\ P (> 9 c e n t s o r s i l v e r) & = (\frac{13}{21} + \frac{12}{21} - \frac{8}{21}) \\ P (> 9 c e n t s o r s i l v e r) & = (\frac{17}{21}) o r 81 % \end{aligned}$

::P(>9美分或银银)=(P(>9美分)+(P(>9美分)+(硅)-P(>9美分和银))P(>9美分或银)P(>9美分或银)=(1321+1221-821)P(>9美分或银)=(1721)或81%

Review
::回顾

1. What is the probability that the outcome of 1 roll of a 10-sided die will be either even or greater than 5?
::1. 1卷10方位死亡的结果甚至甚至或超过5个的概率有多大?

2. What is the probability that the outcome of one roll of a 12 sided die will be either prime or odd?
::2. 12边一卷死亡的结果是质的还是奇的概率是多少?

3. What is the probability of randomly pulling either a king or a heart from a standard deck?
::3. 从标准甲板随意拉动国王或心脏的可能性有多大?

4. What is the probability of randomly pulling either an even numbered card or a black card from a standard deck?
::4. 从标准甲板抽取偶数牌或黑卡的概率是多少?

5. What is the probability that one roll of two standard dice will either result in a number either even or less than 7?
::5. 两张标准骰子一卷的概率是多少? 两张标准骰子一卷的结果是偶数还是小于7?

6. What is the probability that a randomly chosen month will either start with a “J” or have 30 days?
::6. 随机选择的一个月以 " J " 开始或有30天的可能性有多大?

For problems 7 – 11, suppose you have a bag containing 4 blue, 3 green, 5 yellow, and 2 red marbles. All of the green and 2 of the yellow marbles are larger than normal, and 3 of the blue and 1 of the red marbles are smaller than normal.
::对于问题7 — — 11,假设你有一个包,内含4个蓝色、3个绿色、5个黄色和2个红色大理石。所有绿色和2个黄色大理石都大于正常,3个蓝色和1个红色大理石小于正常。

7. What is the probability of randomly pulling a marble that is either large or yellow?
::7. 随意拉扯大理石或黄色大理石的概率有多大?

8. What is the probability that a randomly chosen marble is not large or is yellow?
::8. 随机选择的大理石不大或黄色的可能性有多大?

9. What is the probability that a randomly chosen marble is either small or red?
::9. 随机选择的大理石大小或红色的可能性有多大?

10. What is the probability that a randomly chosen marble is either normally sized or blue?
::10. 随机选择的大理石通常大小或蓝色的可能性有多大?

11. What is the probability that a randomly chosen marble is small or blue?
::11. 随机选择的大理石大小或蓝色的可能性有多大?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。