课程： 8.13 微积分的基本理论原理

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

微积分的基本理论

Velocity due to gravity can be easily calculated by the formula: v = gt , where g is the acceleration due to gravity (9.8m/s ² ) and t is time in seconds. In fact, a decent approximation can be calculated in your head easily by rounding 9.8 to 10 so you can just add a decimal place to the time.
::由于重力造成的速率很容易用公式来计算: v = gt, g 是重力加速度(9.8m/s2), t 是秒以内的时间。事实上,通过四舍五入9.8到10,可以很容易地在你的头上计算出一个像样的近似值,这样您就可以在时间上加上小数位数。

Using this function for velocity, how could you find a function that represented the position of the object after a given time? What about a function that represented the instantaneous acceleration of the object at a given time?
::3⁄4 ̄ ̧漯B

Fundamental Theorem of Calculus
::微积分的基本理论

Antiderivatives
::抗抗药剂

If you think that evaluating areas under curves is a tedious process you are probably right. Fortunately, there is an easier method. In this section, we shall give a general method of evaluating definite integrals (area under the curve) by using antiderivatives.
::如果您认为在曲线下评价区域是一个乏味的过程, 您可能是对的。幸运的是, 有一个比较容易的方法。在本节中, 我们将给出一种一般的方法, 通过使用抗降解剂来评价确定的整体性( 曲线下的区域 ) 。

Definition: The Antiderivative If F ' ( x ) = f ( x ), then F '( x ) is said to be the antiderivative of f ( x ).

There are rules for finding the antiderivatives of simple power functions such as f ( x ) = x ² . As you read through them, try to think about why they make sense, keeping in mind that differentiation reverses integration .
::找到f(x) = x2. 等简单功率函数的抗衍生物有规则。正如您从这些函数中读到的, 试着思考它们为什么有意义, 同时铭记区别会逆转整合。

Rules of Finding the Antiderivatives of Power Functions The Power Rule ::权力规则 $\begin{aligned} \int x^{n} d x = \frac{1}{n + 1} x^{n + 1} + C \end{aligned}$ where C is constant of integration and n is a rational number not equal to -1. A Constant Multiple of a Function Rule ::函数常数多次规则 $\begin{aligned} \int k x^{n} d x = k \int x^{n} d x = k \cdot \frac{1}{n + 1} x^{n + 1} + C \end{aligned}$ where k is a constant. Sum and Difference Rule ::总和和差额和差额 $\begin{aligned} \int [f (x) \pm g (x)] d x = \int f (x) d x \pm \int g (x) d x \end{aligned}$ The Constant Rule ::常数规则 $\begin{aligned} \int k \cdot d x = k x + C \end{aligned}$
where k is a constant. (Notice that this rule comes as a result of the power rule above.)

Rules of Finding the Antiderivatives of Power Functions

The Power Rule
::权力规则

\begin{aligned} \int x^{n} d x = \frac{1}{n + 1} x^{n + 1} + C \end{aligned}

where C is constant of integration and n is a rational number not equal to -1.

A Constant Multiple of a Function Rule
::函数常数多次规则

\begin{aligned} \int k x^{n} d x = k \int x^{n} d x = k \cdot \frac{1}{n + 1} x^{n + 1} + C \end{aligned}

where k is a constant.

Sum and Difference Rule
::总和和差额和差额

\begin{aligned} \int [f (x) \pm g (x)] d x = \int f (x) d x \pm \int g (x) d x \end{aligned}

The Constant Rule
::常数规则

\begin{aligned} \int k \cdot d x = k x + C \end{aligned}

where k is a constant. (Notice that this rule comes as a result of the power rule above.)

The Fundamental Theorem of Calculus
::微积分的基本理论

The Fundamental Theorem of Calculus makes the relationship between and integrals clear. Integration performed on a function can be reversed by differentiation.
::微积分的基本理论使整体体与整体体之间的关系变得清晰明了,对功能的整合可以通过区别对待而逆转。

The Fundamental Theorem of Calculus If a function f ( x ) is defined over the interval [ a , b ] and if F ( x ) is the antidervative of f on [ a, b ], then $\begin{aligned} \int_{a}^{b} f (x) d x = F (x) \|_{a}^{b} \end{aligned}$ $\begin{aligned} = F (b) - F (a) \end{aligned}$

We can use the relationship between differentiation and integration outlined in the Fundamental Theorem of Calculus to compute definite integrals more quickly.
::我们可以利用《微积分基本理论》中概述的差别和融合之间的关系,更快地计算确定的整体体。

Examples
::实例

Example 1
::例1

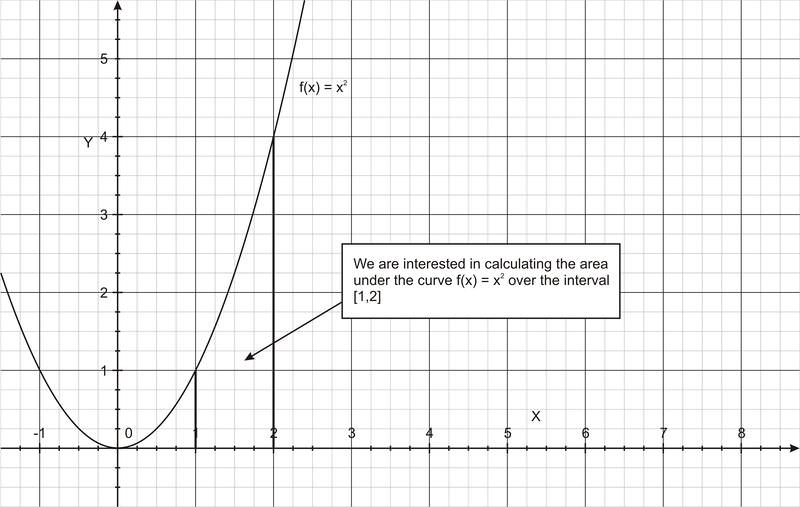
Evaluate $\begin{aligned} \int_{1}^{2} x^{2} d x . \end{aligned}$
::评估12x2dx。

This integral tells us to evaluate the f ( x ) = x ² , which is a parabola over the interval [1, 2], as shown in the figure below.
::如下图所示,本元件要求我们评估 f(x) = x2,这是间隔[1, 2] 的抛物线。

To compute the integral according to the Fundamental Theorem of Calculus, we need to find the of f ( x ) = x ² . It turns out to be F ( x ) = (1/3) x ³ + C , where C is a constant of integration . How can we get this? Think about the functions that will have derivatives of x ² . Take the derivative of F ( x ) to check that we have found such a function. (For more specific rules, see the box after this example). Substituting into the Fundamental Theorem,
::要根据微积分的基本理论计算集成, 我们需要找到 f( x) = x2 的 f( x) = x2 。它被证明是 F( x) = ( 1) x3 + C, C 是常态集成的 C。我们如何得到这个 ? 想想具有 x2 衍生物的函数。使用 F( x) 的衍生物来检查我们找到的函数。 (关于更具体的规则, 请参见此示例后的框 ) 。替换为基本理论 ,

	$\begin{aligned} \int_{a}^{b} f (x) d x \end{aligned}$	$\begin{aligned} = F (x) \|_{a}^{b} \end{aligned}$
	$\begin{aligned} \int_{1}^{2} x^{2} d x \end{aligned}$	$\begin{aligned} = {[\frac{1}{3} x^{3} + C]}_{1}^{2} \end{aligned}$
		$\begin{aligned} = [\frac{1}{3} (2)^{3} + C] - [\frac{1}{3} (1)^{3} + C] \end{aligned}$
		$\begin{aligned} = [\frac{8}{3} + C] - [\frac{1}{3} + C] \end{aligned}$
		$\begin{aligned} = \frac{7}{3} + C - C \end{aligned}$
		$\begin{aligned} = \frac{7}{3} \end{aligned}$

So the area under the curve is (7/3) units ² .
::因此曲线下的区域是(7/3)单位2。

Example 2
::例2

Evaluate $\begin{aligned} \int x^{3} d x . \end{aligned}$
::评估 x3dx。

Since $\begin{aligned} \int x^{n} d x = \frac{1}{n + 1} x^{n + 1} + C \end{aligned}$ , we have
::*xndx=1n+1xn+1+C以来,我们已经有了

	$\begin{aligned} \int x^{3} d x \end{aligned}$	$\begin{aligned} = \frac{1}{3 + 1} x^{3 + 1} + C \end{aligned}$
		$\begin{aligned} = \frac{1}{4} x^{4} + C \end{aligned}$

To check our answer we can take the derivative of $\begin{aligned} \frac{1}{4} x^{4} + C \end{aligned}$ and verify that it is $\begin{aligned} x^{3} \end{aligned}$ , the original function in our integral.
::为了检查我们的答案, 我们可以使用14x4+C的衍生物来验证它是否是x3, 也就是我们整体中的原始函数。

Example 3
::例3

Evaluate $\begin{aligned} \int 5 x^{2} d x . \end{aligned}$
::评估5x2dx。

Using the constant multiple of a power rule, the coefficient 5 can be removed outside the integral:
::使用权力规则的常数倍数,系数5可在整体体之外删除:

$\begin{aligned} \int 5 x^{2} d x = 5 \int x^{2} d x \end{aligned}$
::=5x2dx=5x2dx

Then we can integrate:
::然后我们可以整合:

	$\begin{aligned} = 5 \cdot \frac{1}{2 + 1} x^{2 + 1} + C \end{aligned}$
	$\begin{aligned} = \frac{5}{3} x^{3} + C \end{aligned}$

Again, if we wanted to check our work we could take the derivative of $\begin{aligned} \frac{5}{3} x^{3} + C \end{aligned}$ and verify that we get $\begin{aligned} 5 x^{2} \end{aligned}$ .
::再说一次,如果我们想检查一下我们的工作我们可以拿53x3+C的衍生物来证实我们得到了5x2

Example 4
::例4

Evaluate $\begin{aligned} \int (3 x^{3} - 4 x^{2} + 2) d x . \end{aligned}$
:3x3-4x2+2)dx。

Using the sum and difference rule we can separate our integral into three integrals:
::使用总和和差异规则,我们可以将我们不可分割的组成部分分为三个组成部分:

$\begin{aligned} \int (3 x^{3} - 4 x^{2} + 2) d x = \end{aligned}$
:3x3 - 4x2+2)dx=

$\begin{aligned} 3 (\int x^{3} d x) - 4 (\int x^{2} d x) + (\int 2 d x) \end{aligned}$
::3dx)-4(x2dx)+(2dx)

$\begin{aligned} \to 3 \cdot \frac{1}{4} x^{4} - 4 \cdot \frac{1}{3} x^{3} + 2 x + C \end{aligned}$ $\begin{aligned} \to \frac{3}{4} x^{4} - \frac{4}{3} x^{3} + 2 x + C \end{aligned}$
::314x4-413x3+2x+C34x4-43x3+2xC

Example 5
::例5

Evaluate $\begin{aligned} \int_{2}^{5} \sqrt{x} d x . \end{aligned}$
::评估25xxx。

The evaluation of this integral represents calculating the area under the curve $\begin{aligned} y = \sqrt{x} \end{aligned}$ from x = -2 to x = 3, shown in the figure below.
::该积分的评价表示下图所示曲线y=x下从 x = -2 = x = = 3 的面积的计算。

	$\begin{aligned} \int_{2}^{5} \sqrt{x} d x \end{aligned}$	$\begin{aligned} = \int_{2}^{5} x^{1 / 2} d x \end{aligned}$
	$\begin{aligned} = {[\frac{1}{\frac{1}{2} + 1} x^{1 / 2 + 1}]}_{2}^{5} \end{aligned}$
	$\begin{aligned} = {[\frac{1}{3 / 2} x^{3 / 2}]}_{2}^{5} \end{aligned}$
	$\begin{aligned} = \frac{2}{3} {[x^{3 / 2}]}_{2}^{5} \end{aligned}$
	$\begin{aligned} = \frac{2}{3} [5^{3 / 2} - 2^{3 / 2}] \end{aligned}$
	$\begin{aligned} = 5.57 \end{aligned}$

So the area under the curve is 5.57.
::因此曲线下的区域是5.57。

Example 6
::例6

Use the Fundamental Theorem of Calculus to solve: $\begin{aligned} \int_{4}^{6} \frac{d x}{x} \end{aligned}$ .
::使用微积分的基本理论解析 : 46dxxx。

Given what we know, that if F(x) = ln x, then F'(x) = $\begin{aligned} \frac{1}{x} \end{aligned}$
::根据我们所知如果F(x) = 内x, F'(x) = 1x

Thus, we apply the Fundamental Theorem of Calculus:
::因此,我们适用微积分的基本理论:

$\begin{aligned} \int - 4^{6} \frac{d x}{x} = l n x | - 46 \end{aligned}$
::46dxxx=lnxx*46

= F(6) - F(4) = [ln(6)] - [ln(4)] = 0.4055
::= F(6) - F(4) = [ln(6)] - [ln(4)] = 0.4055

Example 7
::例7

Use the Fundamental Theorem of Calculus to solve: $\begin{aligned} \int_{- 2 p}^{2 p} 3 c o s (x) d x \end{aligned}$ .
::使用微积分的基本理论解析 : @% 2p2p3cos( x) dx 。

Given what we know, that if F(x) = 3sin(x), then F'(x) = 3cos(x)
::根据我们所知,如果F(x) = 3sin(x),那么F'(x) = 3cos(x)

So we apply the Fundamental Theorem of Calculus:
::因此,我们应用微积分的基本理论:

$\begin{aligned} \int_{- 2 p}^{2 p} 3 c o s d x = 3 s i n (x) |_{- 2 p}^{2 p} \end{aligned}$
::=2p2p3costx=3sin(x) =2p2p2p

= F(8) - F(0) = [3sin(2p)] - [3sin(-2p)] = 1 - 0 = 0
::F(8) - F(0) = [3sin(2p)] - [3sin(-2p)] = 1 - 0 = 0

Review
::回顾

Evaluate the integral:
::评估整体:

Evaluate the integral $\begin{aligned} \int_{0}^{3} 5 x d x \end{aligned}$
::评估 =%035xdx

Evaluate the integral $\begin{aligned} \int_{0}^{1} x^{4} d x \end{aligned}$
::评估积分 #%01x4dx

Evaluate the integral $\begin{aligned} \int_{1}^{4} (x - 3) d x \end{aligned}$
::评估#14(x-3)dx

Find the integral:
::查找积分 :

Find the integral of ( x + 1)(2 x - 3) from -1 to 2.
::查找 -1 到 2 的( x + 1)( 2x - 3) 的内装件。

Find the integral of $\begin{aligned} \sqrt{x} \end{aligned}$ from 0 to 9.
::查找 x 从 0 到 9 的积分。

Find $\begin{aligned} \int_{- 1}^{0} - 3 d x \end{aligned}$
::查找 #% 10 - 3dx

Find $\begin{aligned} \int_{- 1}^{3} d x \end{aligned}$
::查找 #%13dx

Find $\begin{aligned} \int_{- p}^{\frac{p}{2}} - 4 c o s (x) d x \end{aligned}$
::查找\\ pp2- 4cos( x) dx

Find $\begin{aligned} \int_{0}^{2} - d x \end{aligned}$
::查找 #% 02- dx

Find $\begin{aligned} \int_{2}^{7} \frac{d x}{x} \end{aligned}$
::查找 # 27dxxx

Find $\begin{aligned} \int_{- 2}^{0} x + 5 d x \end{aligned}$
::查找 20x+5dx

Find $\begin{aligned} \int_{- p}^{\frac{3 p}{2}} 6 s i n (x) d x \end{aligned}$
::查找\\ p3p26sin( x) dx

Find $\begin{aligned} \int_{6}^{7} \frac{d x}{x} \end{aligned}$
::查找 67dxxx

Challenge yourself:
::挑战你自己:

Sketch y = x ³ and y = x on the same coordinate system and then find the area of the region enclosed between them (a) in the first quadrant and (b) in the first and third quadrants.
::在同一坐标系统上,在(a)第一个象限和(b)第一个和第三个象限之间找到区域内的面积,然后在(a)第一个象限和(b)第一个和第三个象限之间找到。

Evaluate the integral $\begin{aligned} \int_{- R}^{R} (π R^{2} - π x^{2}) d x \end{aligned}$ where R is a constant.
::评估 R 是常数的 {RR( R2 x2) dx 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

微积分的基本理论

Fundamental Theorem of Calculus ::微积分的基本理论

Antiderivatives ::抗抗药剂

The Fundamental Theorem of Calculus ::微积分的基本理论

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)