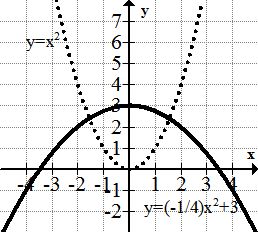课程： 1.2 图形转换 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

图形转换

The basic functions are powerful, but they are extremely limited until you can change them to match any given situation. Transformation means that you can change the equation of a basic function by adding, subtracting, and/or multiplying by constants and thus cause a corresponding change in the graph . What are the effects of the following transformations ?
::基本功能是强大的,但是它们极其有限,直到您能够改变它们来适应任何特定的情况。转换意味着您可以通过添加、减去和(或)乘以常数来改变基本函数的方程式,从而在图形中引起相应的变化。以下转换的效果是什么?

$\begin{align*}f(x) \rightarrow f(x+3)\end{align*}$
:xxx+3)f(x+3)f(x+3)f(x+3)f(x+3)f(x+3)

$\begin{align*}h(x) \rightarrow h(x)-5\end{align*}$
:xx)h(x)-5

$\begin{align*}g(x) \rightarrow -g(2x)\end{align*}$
: gx) \\\\ g(2x)

$\begin{align*}j(x) \rightarrow j \left ( -\frac{x}{2} \right )\end{align*}$
::jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjj

Transforming Functions
::转换函数

A function is a rule that takes any input $\begin{align*}x\end{align*}$ and gives a specific output. When you use letters like $\begin{align*}f\end{align*}$ , $\begin{align*}g\end{align*}$ , $\begin{align*}h\end{align*}$ , or $\begin{align*}j\end{align*}$ to describe the rule, this is called . In order to interpret what effect the algebraic change in the equation will have on the graph, it is important to be able to read those changes in general function notation and then apply them to specific cases.
::函数是一种规则,它需要任何输入 x 并给出特定输出。当您使用 f、 g、 h 或 j 等字母来描述该规则时,该函数被称为。为了解释方程式的代数变化对图形的影响,必须能够用普通函数符号读取这些变化,然后将其应用到具体实例中。

When transforming a function, you can transform the argument (the part inside the " data-term="Parentheses" role="term" tabindex="0"> parentheses with the $\begin{align*}x\end{align*}$ ), or the function itself. There are two ways to linearly transform the argument. You can multiply the $\begin{align*}x\end{align*}$ by a constant and/or add a constant to the $\begin{align*}x\end{align*}$ as shown below:
::当转换函数时,您可以转换参数(括号内有 x 部分)或函数本身。有两种方法可以线性地转换参数。您可以将x乘以一个常数和(或)在 x 中添加一个常数,具体如下:

\begin{aligned} f (x) \to f (b x + c) \end{aligned}

$\begin{align*}f(x) \rightarrow f(bx+c)\end{align*}$
:

fxx)f(bx+c)

The function itself can also be linearly transformed in the same ways:
::函数本身也可以以同样的方式线性转换:

\begin{aligned} f (x) \to a f (x) + d \end{aligned}

$\begin{align*}f(x) \rightarrow af(x)+d\end{align*}$
:

fx) ff(x)+d

Each of the letters $\begin{align*}a,b,c,\end{align*}$ and $\begin{align*}d\end{align*}$ corresponds to a very specific change. Some of these changes are straightforward, while others may be the opposite of what you might expect.
::字母 a, b, c, d 中的每一字母都对应非常具体的变化。其中一些变化是直截了当的, 而其他的则可能与您预期的相反。

$\begin{align*}a\end{align*}$ is a vertical stretch . If $\begin{align*}a\end{align*}$ is negative, there is also a reflection across the $\begin{align*}x\end{align*}$ axis.
::a 是垂直伸展。如果为负,则在 x 轴上方也有反射。

$\begin{align*}d\end{align*}$ is a vertical shift . If $\begin{align*}d\end{align*}$ is positive, then the shift is up. If $\begin{align*}d\end{align*}$ is negative, then the shift is down.
::d 是垂直变化。如果 d 是正, 则向上移动。如果 d 是负, 则向下移动。

When transforming the argument of the function things are more complicated.
::当转换函数事物的参数时更复杂。

$\begin{align*}\frac{1}{b}\end{align*}$ is a horizontal stretch. If $\begin{align*}b\end{align*}$ is negative, there is also a reflection across the $\begin{align*}y\end{align*}$ axis.
::1b 是水平伸展。如果b为负,则在 y 轴之间也有反射。

$\begin{align*}c\end{align*}$ is a horizontal shift . If $\begin{align*}c\end{align*}$ is positive, then the shift is to the left. If $\begin{align*}c\end{align*}$ is negative, then the shift is to the right. Notice that this is the opposite of what most people think at first.
::c 是水平变化。如果 c 是正, 则向左移。如果 c 是负, 则向右移。注意这与大多数人最初的想法相反。

The trickiest part with transforming the argument of a function is the order in which you carry out the transformations. Often it makes sense to apply the transformation to a specific function that is known and then describe the transformation that you see.
::函数参数转换的最关键部分是您执行转换的顺序。通常,将转换应用到已知的特定函数中,然后描述您看到的转换,是有道理的。

The graph below shows the transformation $\begin{align*}f(x) \rightarrow f(3x-6)\end{align*}$ applied to a simple parabola :
::下图显示用于简单抛物线的f(x)f(3x-6)变换:

Clearly the graph is narrower and to the right, but in order to be specific you must look closer. First, notice that the transformation is entirely within the argument of the function. This affects only the horizontal values. This means while the graph seems like it was stretched vertically , you must keep your perspective focused on a horizontal compression .
::显然,图表是窄的,向右的,但为了具体,您必须仔细看一看。首先,请注意,转换完全在函数的参数范围内。这只影响水平值。这意味着,虽然图表看起来是垂直拉伸的,但您必须把视野集中在水平压缩上。

Look carefully at the vertex of the parabola. It has moved to the right two units. This is because first the entire graph was shifted entirely to the right 6 units. Then the function was horizontally compressed by a factor of 3 which means the point (6, 0) became (2, 0) and the $\begin{align*}x\end{align*}$ value of every other point was also compressed by a factor of 3 towards the line $\begin{align*}x = 0\end{align*}$ . This method is counter-intuitive because it requires reading the transformations backwards (the opposite of the way the tells you to).
::仔细查看 parbola 的顶点。它已经移动到右侧的两个单位。这是因为首先整张图被完全移到右侧的 6 个单位。然后函数被水平压缩了3 倍, 这意味着点( 6, 0) 变成 2, 0) , 其他点的 x 值也被压缩到 x=0 线上 3 倍。这种方法是反直观的, 因为它需要向后读取变形( 与告诉您的方式相反 ) 。

Alternatively, the argument can be factored and each component of the transformation will present itself.
::或者,可以将这一论点考虑在内,而转变的每个组成部分本身都会出现。

$\begin{align*}f(3(x-2))\end{align*}$
:3(x- 2))

This time the stretch occurs from the center of the transformed graph, not the origin. This method is ultimately the preferred method.
::此时, 伸展时间会从变形图的中心, 而不是源。此方法最终是首选方法。

Either way, this is a horizontal compression by a factor of 3 and a horizontal shift to the right by 2 units.
::无论哪种方式, 这是水平压缩 3 乘以 3 , 向右水平移动 2 个单位。

Now take the transformation $\begin{align*}f(x) \rightarrow - \frac{1}{4}f(x)+3\end{align*}$ . It describes a vertical stretch by a factor of $\begin{align*}\frac{1}{4}\end{align*}$ , a reflection over the $\begin{align*}x\end{align*}$ axis, and a vertical shift 3 units up. As opposed to what you saw above, the order of the transformations for anything outside of the argument is directly what the order of operations dictates.
::现在选择变换 f( x)\\\ 14f( x)+3 。它描述垂直伸展14 倍, 反射 x 轴, 垂直倾斜 3 个单位向上。与您在上面看到的相反, 任何非参数的变换顺序是操作顺序直接要求的。

First, the parabola is reflected over the $\begin{align*}x\end{align*}$ axis and compressed vertically so it appears wider. Then, every point is moved up 3 units.
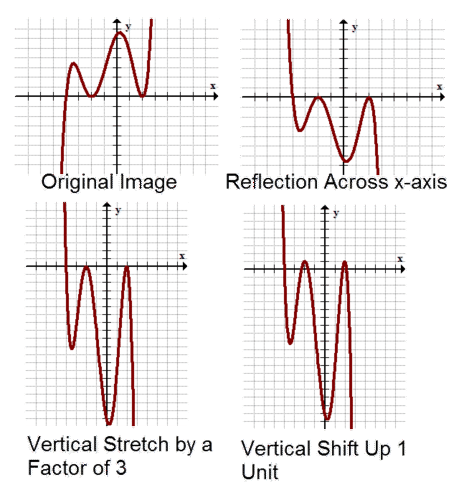
::首先,抛物线在X轴上方反射,垂直压缩,因此看起来更宽。然后,每个点向上移动3个单位。

The transformation $\begin{align*}f(x)\rightarrow- 3f \left ( -\frac{1}{2}x-1 \right )+1\end{align*}$ contains every possible transformation. The horizontal and the vertical components do not interact with each other and so your description of the transformation can begin with either component. Here, start by describing the vertical components of the transformation:
::转换 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以包含每一种可能的转换。水平和垂直的构件不相互作用, 所以您对转换的描述可以从其中任何一个元件开始。在这里, 首先描述转换的垂直构件 :

First , there is reflection across the $\begin{align*}x\end{align*}$ axis and a vertical stretch by a factor of 3. Then, there is a vertical shift up 1 unit. Below is an image of a non-specific function going through the vertical transformations.
::首先, X 轴反射, 垂直伸展为 3 乘以 3 。然后, 垂直向上移动 1 个单位。下面是非特定函数通过垂直转换的图像。

In order to figure out the horizontal components of the transformation, start by factoring the inside of the parentheses (the argument):
::为了找出转换的横向组成部分,首先从括号内乘数(参数)开始:

$\begin{align*}f \left ( -\frac{1}{2} x- 1 \right ) = f \left ( -\frac{1}{2}(x+2) \right )\end{align*}$
:- 12x- 1) = f(- 12( x+2) )

Factoring reveals a reflection across the $\begin{align*}y\end{align*}$ axis, a horizontal shift left 2 units and a horizontal stretch by a factor of 2. Below is an image of the same function going through the horizontal transformations.
::乘法显示 Y 轴的反射, 水平移动左倾 2 个单位, 水平拉伸乘以 2 。下面是通过水平转换的相同函数的图像。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the effects of the following transformations:
::之前,你曾遇到一个问题涉及到以下变化的影响:

$\begin{align*}f(x) \rightarrow f(x+3)\end{align*}$
:xxx+3)f(x+3)f(x+3)f(x+3)f(x+3)f(x+3)

This transformation shifts the entire graph left 3 units. A common misconception is to shift right because the three is positive.
::这种转变使整张图左移了3个单位。常见的误解是右转, 因为三个是正向的。

$\begin{align*}h(x) \rightarrow h(x) -5\end{align*}$
:xx)h(x)-5

This transformation shifts the entire graph down 5 units.
::这种转换将整个图图向下移动5个单位。

$\begin{align*}g(x) \rightarrow -g(2x)\end{align*}$
: gx) \\\\ g(2x)

This transformation is a vertical reflection across the $\begin{align*}x\end{align*}$ axis and a horizontal compression by a factor of 2.
::此转换是横跨 x 轴的垂直反射, 水平压缩为 2 系数。

$\begin{align*}j(x) = j \left ( - \frac{x}{2} \right )\end{align*}$
::j(x)=j(-x2)

This transformation is a horizontal reflection across the $\begin{align*}y\end{align*}$ axis and a horizontal stretch by a factor of 2. A common misconception is to see the $\begin{align*}\frac{1}{2}\end{align*}$ and believe that the $\begin{align*}x\end{align*}$ values will be half as big which is a horizontal compression. However, the $\begin{align*}x\end{align*}$ values need to be twice as big to counteract this factor of $\begin{align*}\frac{1}{2}\end{align*}$ .
::2. 一种常见的误解是看到12,相信x值将大于一半,而x值则等于水平压缩。然而,x值需要是12的两倍,才能抵消12的这一系数。

Example 2
::例2

Describe the following transformation in words: $\begin{align*}g(x) \rightarrow 2 g (-x)\end{align*}$
::以单词描述以下转换: g(x)___2g(-x)

Vertical stretch by a factor of 2 and a reflection across the $\begin{align*}y\end{align*}$ axis.
::垂直伸展乘以 2 , 反射横跨 y 轴。

Example 3
::例3

Describe the transformation that would change $\begin{align*}h(x)\end{align*}$ in the following ways:
::描述以下列方式改变h(x)的变换:

Vertical compression by a factor of 3.
::垂直压缩3乘以3。

Vertical shift down 4 units.
::垂直向下移动4个单位

Horizontal shift right 5 units.
::水平向右移5个单位。

$\begin{align*}\frac{1}{3}h(x-5)-4\end{align*}$
::13h(x-5-5)-4

Example 4
::例4

Describe the transformation that would change $\begin{align*}f(x)\end{align*}$ in the following ways:
::说明以下列方式改变f(x)的变换:

Horizontal stretch by a factor of 4 and a horizontal shift 3 units to the right.
::水平伸展为 4 乘以 4 , 水平向右移动 3 单位。

Vertical reflection across the $\begin{align*}x\end{align*}$ axis and a shift down 2 units.
::垂直反射横跨 x 轴, 向下移动 2 个单位。

$\begin{align*}-f \left ( \frac{1}{4}(x -3)\right ) -2\end{align*}$ or $\begin{align*}-f \left ( \frac{1}{4}x -\frac{3}{4}\right ) -2\end{align*}$
::-f(14(x-3))-2或-f(14x-34)-2

Summary

Transforming functions involves changing the equation of a basic function like adding or multiplying by constants, which causes a corresponding change in the graph.
::变换函数涉及改变基本函数的方程式,如增加或乘以常数,从而导致图中的相应变化。

Transformations can be applied to the argument (inside the parentheses) or the function itself, with each letter (a, b, c, d) representing a specific change.
::变式可适用于参数(括号内)或函数本身,每个字母(a、b、c、d)代表具体变化。

The order of transformations matters, especially when transforming the argument of a function. Factoring the argument can help reveal the specific transformations applied.
::转换的顺序很重要,特别是在转换函数的参数时。

Review
::回顾

Describe the following transformations in words.
::描述以下文字的变换。

1. $\begin{align*}g(x) \rightarrow -g(-x)\end{align*}$
::1. g(x)__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2. $\begin{align*}f(x) \rightarrow -f(x+3)\end{align*}$
::2. f(x)f(x+3)

3. $\begin{align*}h(x) \rightarrow h(x+1)-2\end{align*}$
::3.h(x+1)-2

4. $\begin{align*}j(x) \rightarrow j(-x+3)\end{align*}$
::4. j(xx)j(-x+3)

5. $\begin{align*}k(x) \rightarrow - k(2x)\end{align*}$
::5. k(x)\\\ k( 2x)

6. $\begin{align*}f(x) \rightarrow 4 f \left ( \frac{1}{2}x + 1 \right )\end{align*}$
::6. f(x)4f(12x+1)

7. $\begin{align*}g(x) \rightarrow -3g(x-2)-2\end{align*}$
::7. g(x)_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

8. $\begin{align*}h(x) \rightarrow 5h (x+1)\end{align*}$
::8. h(x)5h(x+1)

9. Describe the transformation that would change $\begin{align*}h(x)\end{align*}$ in the following ways:
::9. 描述以下列方式改变h(x)的转变:

Vertical stretch by a factor of 2
::垂直伸展乘以 2

Vertical shift up 3 units.
::垂直向上移动3个单元。

Horizontal shift right 2 units.
::水平向右移动 2 个单位。

10. Describe the transformation that would change $\begin{align*}f(x)\end{align*}$ in the following ways:
::10. 说明以下列方式改变f(x)的变换:

Vertical reflection across the $\begin{align*}x\end{align*}$ axis.
::X轴的垂直反射。

Vertical shift down 1 unit.
::垂直向下移动 1 个单位。

Horizontal shift left 2 units.
::横向左转 2 个单位。

11. Describe the transformation that would change $\begin{align*}g(x)\end{align*}$ in the following ways:
::11. 描述以下列方式改变g(x)的变换:

Vertical compression by a factor of 4.
::垂直压缩为4系数。

Reflection across the $\begin{align*}y\end{align*}$ axis.
::反射在Y轴上方

12. Describe the transformation that would change $\begin{align*}j(x)\end{align*}$ in the following ways:
::12. 说明以下列方式改变j(x)的转变:

Horizontal compression by a factor of 3.
::水平压缩乘以 3。

Vertical shift up 3 units.
::垂直向上移动3个单元。

Horizontal shift right 2 units.
::水平向右移动 2 个单位。

13. Describe the transformation that would change $\begin{align*}k(x)\end{align*}$ in the following ways:
::13. 描述以下列方式改变 k(x) 的变换:

Horizontal stretch by a factor of 4.
::水平伸展以4为因数。

Vertical shift up 3 units.
::垂直向上移动3个单元。

Horizontal shift left 1 unit.
::左1单位水平向左移动。

14. Describe the transformation that would change $\begin{align*}h(x)\end{align*}$ in the following ways:
::14. 描述以下列方式改变h(x)的转变:

Vertical compression by a factor of 2.
::垂直压缩乘以 2。

Horizontal shift right 3 units.
::水平向右移3个单位。

Reflection across the $\begin{align*}y\end{align*}$ axis.
::反射在Y轴上方

15. Describe the transformation that would change $\begin{align*}f(x)\end{align*}$ in the following ways:
::15. 描述以下列方式改变f(x)的转变:

Vertical stretch by a factor of 5.
::垂直伸展以5为因数。

Reflection across the $\begin{align*}x\end{align*}$ axis.
::X轴反射。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

图形转换

Transforming Functions ::转换函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)