7.6 宗学实验

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 分子实验

  Collapse Expand

  分子实验

  播放段落

  Binomial experiments are very popular for studies because the probability of one possibility or the other can be calculated quickly and accurately. How do you identify a binomial experiment? Can an experiment that is not binomial be easily converted into a binomial experiment?
  ::二进制实验在研究中非常受欢迎,因为一种可能性的概率可以快速和准确地计算。您如何识别二进制实验?非二进制实验可以很容易地转换成二进制实验吗?

  播放段落

  Look to the end of the lesson for the answer.
  ::寻找教训的结尾 以找到答案。

  播放段落

  Binomial Experiments 
  ::分子实验

  播放段落

  Binomial experiments give rise to binomial random variables , which will be the topic of our next couple of lessons. A binomial experiment is a very specific type of experiment. In order to be a binomial experiment, there are four qualifications that the experiment must meet:
  ::二进制实验产生二进制随机变数,这是我们接下来几个课程的主题。二进制实验是一种非常特殊的实验类型。要成为二进制实验,实验必须满足四个条件:

  播放段落
  1. There must be a fixed number of trials . The experiment cannot just be to roll a die until you get a 2, because the number of rolls (trials) is not fixed.
     ::试验必须有一个固定的试验次数。 实验不能仅仅在获得 2 之前滚死, 因为卷数( 审判) 没有固定 。
  播放段落
  2. Each trial must be independent of the others. You cannot have a situation like “If you flip a coin and get heads, flip twice more, and if you get tails, flip three more times”.
     ::每个审判必须独立于其他审判。 你不能有这样的情况:“如果你翻硬币并获得头部,翻两次,如果你得到尾巴,翻三次”。
  播放段落
  3. Each trial must have a “success” and a “failure”. Depending on the trial, these may be identified as “yes” and “no” or “0” and “1” or “black” and “white”, etc. However, from a statistics standpoint, the outcome you are studying is generally called the “success” and the other is called “failure”.
     ::每个审判必须有一个“成功”和“失败”,视审判情况而定,这些可以被确定为“是”和“否”或“0”和“1”或“黑人”和“白人”等,然而,从统计的角度来看,你正在研究的结果一般称为“成功”,另一个称为“失败”。
  播放段落
  4. The probability of success must be the same for all trials. The experiment cannot be 10 trials of pulling and keeping a card from a deck to see how many are hearts, because the probability of getting a heart would change each trial. To make this a binomial experiment, you need to replace the card each time.
     ::成功概率必须是所有试验的相同概率。 实验不能是从甲板上拉动和保留一张牌以查看有多少是心的10次试验, 因为获得心脏的概率会改变每一次试验。 要将它变成二进制实验, 您需要每次更换牌。

  播放段落

  Identifying Binomial Random Variables 
  ::识别分义随机变量

  播放段落

  1. If a fair coin if flipped 10 times, and  $\begin{align*}T\end{align*}$ is the number of tails, is $\begin{align*}T\end{align*}$ a binomial random variable ?
  ::1. 如果一个公平硬币翻了10次,而T是尾数,那么T是一个二进制随机变数吗?

  播放段落

  Yes,  $\begin{align*}T\end{align*}$ is a binomial random variable, and this is a binomial experiment. It meets all four qualifications:
  ::是的,T是一个二进制随机变量,这是一个二进制实验。它符合所有四种条件:

  播放段落
  1. There is a specific number of trials: 10 flips
     ::有具体数目的审判:10次翻案
  播放段落
  2. Trials are independent: the outcome of one coin flip does not affect the next flip
     ::审判是独立的:一个硬币翻转的结果不影响下一个翻转
  播放段落
  3. There are only two possible outcomes: a “success” and “failure”. Since we are counting tails, every tails is a “success” and every heads is a “failure”
     ::可能的结果只有两种:“成功”和“失败”,因为我们在计算尾巴,每个尾巴都是“成功”,每个头都是“失败”
  播放段落
  4. The probability is the same for all trials: The probability of getting tails is always 50% if flipping a fair coin
     ::所有试验的概率都是一样的:如果抛出一个公平的硬币,获得尾巴的概率总是50%。

  播放段落

  2. If Trina designates  $\begin{align*}Y\end{align*}$ to be the number of yellow marbles she gets during nine trials of randomly pulling 1 marble from a bag filled with marbles of various colors and returning it, is  $\begin{align*}Y\end{align*}$ a random variable ? Is it binomial?
  ::2. 如果Trina指定Y为她9次随机抽取1大理石的黄色大理石,从装满各种颜色的大理石的袋子中抽取1大理石,然后还回去,Y是一个随机变量吗?它是二元论的吗?

  播放段落

  Yes, $\begin{align*}Y\end{align*}$ is a random variable, since it is the random numerical result of a limited number of independent trials of an experiment. It is also binomial, since each of the limited trials is independent, has a success/failure (yellow/not yellow), and has the same probability of success.
  ::是的,Y是一个随机变量,因为它是一个实验独立试验数量有限的随机数字结果。它也是二元论,因为每个有限的试验都是独立的,成功/失败(黄/黄/黄),成功概率相同。

  播放段落

  Finding Unknown Values 
  ::查找未知值

  播放段落

  If  $\begin{align*}N\end{align*}$ is the number of nines you get when rolling two standard dice three times:
  ::如果 N 是滚动双标准骰子三次时得到的 9 个数 :

  播放段落
  1. Is $\begin{align*}N\end{align*}$ a binomial random variable?
     ::一个二进制随机变量吗?
  播放段落
  2. What are the possible values of $\begin{align*}N\end{align*}$ ?
     ::N的可能价值是什么?
  播放段落
  3. Create a histogram or pie chart showing the probability distribution of $\begin{align*}N\end{align*}$ .
     ::创建直方图或饼图,显示 N 的概率分布 。

  播放段落

  a. Is  $\begin{align*}N\end{align*}$  a binomial random variable?
  ::a. N是一个二进制随机变数吗?

  播放段落

  $\begin{align*}N\end{align*}$ is a binomial random variable, because it is the result of a specific and limited number of independent trials of a random process and each outcome is either nine or not nine.
  ::N是一个二进制随机变量,因为它是随机过程的个别和有限的独立试验的结果,每个结果有9个或9个。

  播放段落

  b. What are the possible values of  $\begin{align*}N\end{align*}$ ?
  ::b. N的可能值是什么?

  播放段落

  Since you could only roll a total of 9 once each trial,  $\begin{align*}N\end{align*}$ could be 0, 1, 2, or 3.
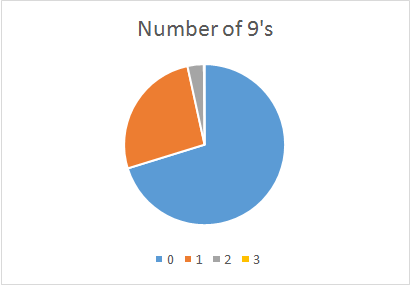
  ::因为每次审判,你只能卷9次, N可能是0, 1, 2, 或3次。

  播放段落

  c. Create a histogram or pie chart showing the probability distribution of  $\begin{align*}N\end{align*}$ . 
  ::c. 创建直方图或饼图,显示N的概率分布。

  播放段落

  The probabilities of each of the possible values of $\begin{align*}N\end{align*}$ would be:
  ::每一可能值的概率为:

  播放段落

  (see the lesson: Understanding Discrete Random Variables, Example C, for the calculations)
  :见教训:了解分辨随机变量,用于计算)

  播放段落
  • $\begin{align*}N=0: \frac{512}{729}\end{align*}$
    ::N=0:512729
  播放段落
  • $\begin{align*}N=1: \frac{192}{729}\end{align*}$
    ::N=1:192729
  播放段落
  • $\begin{align*}N=2: \frac{24}{729}\end{align*}$
    ::N=2:24729
  播放段落
  • $\begin{align*}N=3: \frac{1}{729}\end{align*}$
    ::N=3:1729

  播放段落

  A pie chart would look like this: (note that total probability = $\begin{align*}\frac{512}{729} + \frac{192}{729} + \frac{24}{729} + \frac{1} {729} = \frac{729}{729}\end{align*}$ ).
  ::馅饼图表将看起来是这样的注意总概率=512729+192729+24729+1729=729729)。

  

  播放段落

  Earlier Problem Revisited
  ::重审先前的问题

  播放段落

  Binomial experiments are very popular for studies because the probability of one possibility or the other can be calculated quickly and accurately. How do you identify a binomial experiment? Can an experiment that is not binomial be easily converted into a binomial experiment?
  ::二进制实验在研究中非常受欢迎,因为一种可能性的概率可以快速和准确地计算。您如何识别二进制实验?非二进制实验可以很容易地转换成二进制实验吗?

  播放段落

  A binomial experiment must consist of a limited number of independent trials, where each trial outcome is either a success or a failure, and each trial has the same probability of success as all other trials.
  ::二元实验必须包括数量有限的独立审判,其中每个审判结果要么成功要么失败,每个审判成功的可能性与所有其他审判相同。

  播放段落

  A non-binomial experiment can often be viewed as binomial by carefully stating the outcome of each trial in a binomial format. For example, a non-binomial experiment might be “Count the number of heads and tails resulting from 8 flips of a fair coin”. Viewed as a binomial experiment, the same results could be collected from “How many tails do you get by flipping a fair coin 8 times”? You could then subtract the result from 8 to get the number of “not tails”, e.g. “heads”.
  ::非二元实验通常可以被视为二元实验,以二元形式仔细说明每次试验的结果,例如,非二元实验可以是“计算公平硬币8个翻转产生的头部和尾部的数量”。 作为一种二元实验,可以从“翻开公平硬币8次,有多少尾部会得到多少次”中收集同样的结果。 然后,你可以从8个中减去结果,以获得“非尾部”的数目,例如“头部”。

  播放段落

  Examples 
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Mariska spins a spinner 40 times, recording the number of 4’s she gets. Is this a binomial experiment?
  ::Mariska旋转了一个旋转器40倍,记录了她得到的四分位数。这是二进制实验吗?

  播放段落

  Yes, this is a binomial experiment because Mariska is conducting a limited number of independent random "4" or "not 4" trials, and the probability of spinnig a "4" does not change.
  ::是的,这是一个二进制实验, 因为Mariska正在进行数量有限的 独立的随机“4”或“非4”试验, 脊柱“4”的概率没有改变。

  播放段落

  Example 2
  ::例2

  播放段落

  Heidi has a bag containing 4 blue, 3 green, 5 red, and 7 yellow marbles. She defines a trial as pulling a marble, recording the color, and replacing it. She records the number of trials it takes to pull a green marble. Is this a binomial experiment?
  ::海蒂有一个装有4个蓝色、3个绿色、5个红色和7个黄色大理石的袋子。 她将试验定义为拉大理石、记录颜色并替换它。 她记录了拉绿色大理石需要多少试验。 这是二元论实验吗?

  播放段落

  No, Heidi is not conducting a binomial experiment because the number of trials is not specified, she just keeps pulling until she gets a green.
  ::不,海蒂没有进行二进制实验 因为试验数量没有说明 她只是不停地拉 直到她得到绿色。

  播放段落

  Example 3
  ::例3

  播放段落

  Evan notes that 24% of online game players he polled are between 30 and 39 years old. Evan decides to create a team of players from that age range by randomly choosing names from among those he polled, keeping each one he chooses that is in his/her 30’s. If he chooses a name only 10 times, no matter the number of players he gets, is this a binomial experiment?
  ::埃文指出,他所选的网上游戏玩家中,24%的人年龄在30至39岁之间。 埃文决定通过随机从他所选的球员中选取名字,将他所选的每一个名字保留在30年代。 如果他只选了10次名字,不管他得到多少球员,这是二元论实验吗?

  播放段落

  No, Evan is not conducting a binomial experiment because the probability that a random player will be between 30 and 39 changes each tim ehe keeps one for his team. 
  ::不,埃文不是在做一个二进制实验 因为随机玩家在30到39之间 的概率会改变 每一个timehe 为其团队保留一个。

  播放段落

  Review 
  ::回顾

  播放段落

  For questions 1-12, state that a particular experiment is or why it is not binomial:
  ::对于问题1-12, 说明某一特定实验是二元实验, 或为什么它不是二元实验:

  播放段落
  1. A spinner has a 35% probability of landing on blue. Let  $\begin{align*}B\end{align*}$ be the number of blues spun in 5 spins.
     ::旋转器在蓝色上着陆的概率为35%。 B 是蓝色在5个旋转时的旋转次数 。
  播放段落
  2. A bag contains 6 blue, 4 green, and 3 red candies. Let  $\begin{align*}G\end{align*}$ be the number of green candies you pull out and eat in 5 trials.
     ::包里装有6个蓝色、4个绿色和3个红色糖果。让G成为5次试验中你拿出来吃绿色糖果的数量。
  播放段落
  3. One trial of an experiment consists of pulling a random card from a standard deck, noting it, and replacing it, you conduct 12 trials.
     ::实验的试验之一是从标准甲板上抽取一张随机卡片,注明并替换它,进行12次试验。
  播放段落
  4. One trial consists of pulling two cards from a standard deck, noting them, and replacing them. Let  $\begin{align*}T\end{align*}$ be the number of trials until you pull two face cards at the same time.
     ::其中一项审判包括从标准甲板上拉出两张卡片,注明并替换它们。让T成为审判的数量,直到你同时拉出两张脸卡。
  播放段落
  5. A 20-sided die is rolled ten times, and  $\begin{align*}S\end{align*}$ is the number of sevens rolled.
     ::20方死亡是十倍,七方死亡是七方死亡。
  播放段落
  6. Assume that 15% of word game players create at least 12 words out of 50 that have more than 5 letters, and you let  $\begin{align*}W\end{align*}$ be the number of letters in words from 20 trials of 1 game each.
     ::假设15%的单词游戏玩家在50个有超过5个字母的单词中 创造出至少12个字, 你让W成为20个字数的字母数, 每个字数为1个。
  播放段落
  7. A die is rolled 20 times. What is the probability of rolling a 1 exactly 5 times?
     ::死亡是滚动20次。滚动1次的概率是多少? 确切的说是5次?
  播放段落
  8. You plan on choosing students (with replacement) from a population of 28, 17 of which are Juniors. You want to know how many will have to be picked before getting a Junior.
     ::您计划从28人中选择学生( 替换学生 ) , 其中17人是青年。 您想知道在获得青年之前需要挑选多少人 。
  播放段落
  9. A new reality show is so popular that an estimated 47% of households watch it every week. You choose 20 households at random. Let  $\begin{align*}X\end{align*}$ be the number of households watching the show.
     ::新的现实节目非常流行,估计有47%的家庭每周都看。您随机选择20个家庭。让X成为观看节目的家庭数量。
  播放段落
  10. $\begin{align*}H\end{align*}$  is the number of heads tallied over ten flips of a fair coin.
      ::H 是一个公平硬币的十张硬币的 头数。
  播放段落
  11. $\begin{align*}F\end{align*}$  is the number of 5’s you roll before rolling a 6, on a standard die.
      ::F是按标准死亡时在滚动6之前滚动的5个数字。
  播放段落
  12. $\begin{align*}O\end{align*}$  is the number of 1’s you roll in fifteen rolls of a standard die.
      ::O是标准死亡的15卷中你滚动的1号数。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。