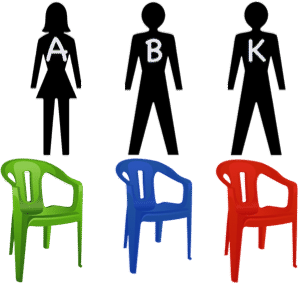课程： 8.2 计算变换 | The Way To Learn

The Way To Learn

首页日程管理

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节计算间替

折叠展开
计算间替
If the Olympic High Jump has 24 semifinalists, how many possible ways can the competitors be arranged into Gold, Silver, and Bronze winners?
::如果奥运高跳赛有24名半决赛选手,

This is a calculation, by the end of the lesson you will have no problem calculating the answer.
::这是一个计算, 在课程结束时, 您在计算答案时不会有问题。

Calculating Permutations
::计算间替

Calculating the number of permutations possible from a group of objects is a rather simple calculation, but understanding the concept can be a little tricky.
::从一组天体中计算可能的变异数量是一个相当简单的计算方法,但理解这一概念可能有点困难。

One way to understand the concept is to think of a group of friends seated around a table. If there are three friends and three seats, then the number of ways the friends can sit around the table is a question of permutations.
::理解这个概念的一个方法就是想象一群朋友坐在桌边。如果有三个朋友和三个座位,那么朋友坐在桌边的方式就是一个变数问题。

Suppose the friends are Amber, Brian, and Kelli, and the chairs are one each green, blue, and red.
::假设朋友是安珀、布莱恩和凯利椅子是绿色、蓝色和红色的

Let’s consider the options, starting with Amber in the green chair:
::让我们从绿椅子上的琥珀开始考虑这些选项:

$\begin{aligned} 1. Green: Amber, & blue: Brian, & red: Kelli \\ 2. Green: Amber, & red: Brian, & blue: Kelli \\ 3. Blue: Amber, & green: Brian, & red: Kelli \\ 4. Blue: Amber, & red: Brian, & green: Kelli \\ 5. Red: Amber, & blue: Brian, & green: Kelli \\ 6. Red: Amber, & green: Brian, & blue: Kelli \end{aligned}$

::1. 绿色:Amber,蓝色:Brian,红色:Kelli2.绿色:Amber,红色:Brian,蓝色:Kelli3.蓝色:Amber,绿色:Brian,红色:Kelli4.蓝色:Amber,红色:Brian,绿色:Kelli5.红色:Amber,蓝色:Brian,绿色:Kelli6.红色:Amber,绿色:Brian,蓝色:Kelli:Kelli。

There are six permutations. We can see that each time the first color is chosen, there are two possibilities left for the next person to choose from, and the last person does not get to choose. That’s why there are two of each color in each column. If Amber chooses green, then Brian can either choose blue, leaving red for Kelli, or Brian can choose red, leaving blue for Kelli. The same goes for Amber choosing blue or red. Each time, Brian has two colors left to choose from, and Kelli gets the remaining color. The chart would look the same regardless of who chooses first, because no matter who the first person is, there are only two ways the others could sit, meaning there should be (and are) two entries for each color under each person’s name.
::我们可以看到,每次选择第一个颜色时,下一个人可以选择两个可能的颜色,最后一个人不能选择。这就是为什么每列有两种颜色。如果Amber选择绿色,那么Brian可以选择蓝色,让Kelli选择红色,让Kelli选择红色,让Kelli选择蓝色。Amber选择蓝色或红色也是一样。Brian选择了两个颜色,Kelli选择了其余的颜色。不管谁先选择,图表将看起来相同,因为不管谁先选择,其他人只能用两种方式坐下,这意味着每个人的名字下每个颜色应该有两个条目(和两个条目 ) 。

Fortunately, we don’t need to draw out a diagram every time we want to find the number of permutations possible in a situation like this. As long as there are no duplicates or items so similar they can’t be told apart (two green chairs, for instance), all we need to know is how to use .
::幸运的是,我们不需要每次在这样的情况下寻找可能的变异数量时都绘制图表。只要没有复制件或类似的东西无法分开(比如两张绿色椅子 ) , 我们只需要知道如何使用。

Factorials are notated with an exclamation point “!”, and they indicate that you should start with the number before the exclamation point, and count down to 1, multiplying each number by the next. For instance, the first few factorials are:
::阶乘加一个感叹点“! ! ” , 表示您应该从感叹点之前的数开始, 倒数倒数到 1, 然后乘以每个数乘以下一个数。例如, 前几个因数是:

$\begin{aligned} 0! = 1 (b y d e f i n i t i o n) \\ 1! = 1 \\ 2! = 2 \times 1 = 2 \\ 3! = 3 \times 2 \times 1 = 6 \\ 4! = 4 \times 3 \times 2 \times 1 = 24 \\ 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \end{aligned}$

::0!=1 (定义) 1!=1 2!=2x1=2 3;=3x2x1=6 4;=4x3x2x2x1=245;=5x4x3x3x3x2x1=120

To calculate the number of permutations possible given $\begin{aligned} n \end{aligned}$ non-repeating values, calculate $\begin{aligned} n! \end{aligned}$ .
::要计算给n的非重复值可能的变换次数,请计算 n!

To calculate the number of permutations of $\begin{aligned} r \end{aligned}$ values from set $\begin{aligned} n \end{aligned}$ , calculate the first $\begin{aligned} r \end{aligned}$ numbers of $\begin{aligned} n! \end{aligned}$
::要从 set n 计算 r 值的变换次数, 请计算 n 的第一个 r 数字 !

Alternatively, the formula for counting permutations is:
::或者,计算变差的公式是:

$\begin{aligned} \frac{n!}{(n - r)!} \end{aligned}$

::不! (r)!

Where $\begin{aligned} n \end{aligned}$ is the number of available values, and $\begin{aligned} r \end{aligned}$ is the number of values to be selected.
::此处 n 是可用数值的数量, r 是要选择的数值数量。

You may also see this information in the form: $\begin{aligned} _{n} P_{r} \end{aligned}$
::您也可以在下列表格中看到此信息:nPr

Real-World Application: Line
::真实世界应用程序: 行

How many ways can six people line up as they wait in line to buy tickets?
::六个人在排队等票的时候还能排多少队?

Since this is a basic permutation question, with no duplicates and no indistinguishable members, all we need to do is find six :
::由于这是一个基本的变异问题,没有重复,没有无法区分的成员,我们需要做的就是找到六个:

$\begin{aligned} 6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720 \end{aligned}$

There are 720 ways that six people could line up.
::有720种方法 6个人可以排队

Rearranging Words
::重新排列单词

How many ways can the letters in the word “ factory” be arranged?
::“设施”一词中的字母可以安排多少种方式?

“ factory” has seven letters, all unique, and we want the possible number of arrangements using all seven, so the number of permutations is seven factorial:
::“设施”有7个字母,都是独一无二的,我们需要使用所有7个的可能的安排数目,因此变换数目是7个因素:

$\begin{aligned} 7! = 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 5040 \end{aligned}$

There are 5,040 ways to arrange the letter in the word “ factory ”.
::有5 040种方法将信件安排在“设施”一词内。

Permutations from Words
::字词的变换

How many different three-letter permutations are possible using the letters in the word “ bread” ?
::使用“面包”一词中的字母可以使用多少种不同的三字母排列?

This is a slightly different problem than the first two, since we aren’t looking for permutations using all five letters. Since we are only selecting three of the five letters for each arrangement, there will be fewer possible arrangements. As I mentioned at the end of the “Guidance” section, there are a couple of ways to view this type of problem:
::这个问题与前两个问题略有不同,因为我们并不是要用所有五个字母来寻找变异。由于我们只为每个安排选择了五个字母中的三个,因此可能的安排会更少。正如我在“指导”一节结尾提到的,我们有几种方法来看待这类问题:

Conceptually, we need to calculate only the first three numbers of five factorial:
::从概念上说,我们只需要计算前三个数字即五个因数:

$\begin{aligned} 5 \times 4 \times 3 = 120 \end{aligned}$

Using the formula: $\begin{aligned} \frac{n!}{(n - r)!} \end{aligned}$
::使用公式: n! !

$\begin{aligned} \frac{5!}{(5 - 3)!} \\ \frac{5!}{2!} \\ \frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1} \\ 5 \times 4 \times 3 = 60 \end{aligned}$

There are 60 three-letter permutations of the letters in the word “bread”.
::在“面包”一词中,字母有60个字母的三字母排列。

Earlier Problem Revisited
::重审先前的问题

If the Olympic High Jump has 24 semifinalists, how many possible ways can the competitors be arranged into Gold, Silver, and Bronze winners?
::如果奥运高跳赛有24名半决赛选手,

For this question, we need to calculate the number of permutations of three competitors out of the set of 24 semifinalists. Since we only want arrangements of three, we need to calculate the first three numbers in 24!
::对于这个问题,我们需要计算24个半决赛选手中3个竞争对手的变异数目。由于我们只想要3个,我们需要计算24个的前3个数字!

$\begin{aligned} 24 \times 23 \times 22 = 12, 144 \end{aligned}$

There are 12,144 possible gold, silver, bronze rankings of the 24 semifinalists.
::24名半决赛选手中可能有12 144名金、银、铜排名。

Examples
::实例

Example 1
::例1

How many ways can the letters in "education" be arranged?
::在“教育”中,可以用多少方式安排字母?

There are nine letters in “education”, so we need to calculate 9!:
::在“教育”中有九个字母, 所以我们需要计算九!

$\begin{aligned} 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 362, 880 \end{aligned}$

Example 2
::例2

How many different four letter arrangements can be made from the word "document"?
::从“文件”一词中可以作出多少不同的四个字母安排?

There are eight letters in “document”, but we only want arrangements of four, so we calculate the first four numbers of 8!:
::在“文件”中有8个字母, 但我们只需要4个, 所以我们计算前4个数字是8!

$\begin{aligned} 8 \times 7 \times 6 \times 5 = 1, 680 \end{aligned}$

Example 3
::例3

How many permutations are represented by $\begin{aligned} _{8} P_{5} \end{aligned}$ ?
::8P5代表了多少变数?

$\begin{aligned} _{8} P_{5} \end{aligned}$ is read as “pick five items from the eight available”. The formula for permutations is $\begin{aligned} \frac{n!}{(n - r)!} \end{aligned}$ :
::8P5改为“从现有的8个项目中选取5个项目”。

$\begin{aligned} \frac{8!}{(8 - 5)!} \\ \frac{8!}{3!} \\ \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1} \\ 8 \times 7 \times 6 \times 5 \times 4 = 6720 \end{aligned}$

Example 4
::例4

How many different ways can the basic colors of a rainbow: red, orange, yellow, green, blue, indigo, and violet, be arranged?
::彩虹的基本颜色可以安排多少种不同的方式:红色、橙色、黄色、绿色、绿色、蓝色、印地戈和紫罗兰?

There are seven colors in a basic rainbow, and we are looking for the number of unique permutations of all seven.
::基本彩虹里有七种颜色, 我们正在寻找所有七种不同的颜色。

$\begin{aligned} 7! = 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 5, 040 \end{aligned}$

Review
::回顾

For all questions 1-13, assume no duplicated units are allowed.
::对于所有问题1-13,假设不允许重复单位。

All the answers for a 5 question multiple - choice test are A, B, C, or D. Find the number of possible answer keys a teacher could have.
::5个问题多个答案的所有答案 - 选择测试是 A、 B、 C 或 D。找出教师可能拥有的答案键数。

Calculate 6!
::计算六!

Calculate 4!
::计算四!

You are distributing from a group of 5 items one to each of 2 people. How many different ways can you do this?
::你从一组5件物品中向2个人每人分配1件。你能用多少种不同的方法来做到这一点?

Calculate $\begin{aligned} _{6} P_{3} \end{aligned}$
::计算 6P3

Find the number of permutations of 7 distinct items.
::查找7个不同项目的变换次数。

To unlock a school locker, you need a locker combination consisting of 3 unique numbers from 1 to 9. How many possible locker combinations are there?
::要打开学校储物柜, 你需要一个储物柜组合由3个独有号码组成从1到9

Calculate $\begin{aligned} _{6} P_{2} \end{aligned}$
::计算 6P2

Calculate $\begin{aligned} _{8} P_{8} \end{aligned}$
::计算 8P8

If a bank account number consists of seven unique digits 0-9, how many possible accounts are there?
::如果银行账户号码由7个独有数字 0 -9组成,有多少个可能的账户?

For a dinner party, you need to make a seating arrangement of 9 people. Find the number of different ways of arranging the party.
::晚宴上,你需要安排9人的座位, 找出安排晚会的不同方式。

Why can’t you calculate 4.5! ?
::为何不能计算4.5?

How many five-letter arrangements can be made from the word “number”?
::从“数目”一词中可以作出多少五字母安排?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。