课程： 1.8 零职能和职能的拦截

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

零职能和零职能拦截

An intercept in mathematics is where a function crosses the $\begin{aligned} x \end{aligned}$ or $\begin{aligned} y \end{aligned}$ axis. What are the intercepts of this function?
::数学截取符是函数通过 xor 偏移的函数。该函数的截取符是什么 ?

X and Y Intercepts
::X Y 和 X Y 拦截器

The first type of intercept you may have learned is the $\begin{aligned} y \end{aligned}$ -intercept when you learned the intercept form of a line: $\begin{aligned} y = m x + b \end{aligned}$ . A $\begin{aligned} y \end{aligned}$ -intercept is the unique point where a function crosses the $\begin{aligned} y \end{aligned}$ axis. It can be found algebraically by setting $\begin{aligned} x = 0 \end{aligned}$ and solving for $\begin{aligned} y \end{aligned}$ .
::您可能已经学到的第一种拦截类型是当您学习到一条线的拦截形式时的 Y 拦截 : y=mx+b. A y 拦截是函数跨越 y 轴的独特点。通过设置 x=0 和 y 的解答, 可以找到代数。

$\begin{aligned} x \end{aligned}$ -intercepts are where functions cross the $\begin{aligned} x \end{aligned}$ axis and where the height of the function is zero. They are also called roots, solutions and zeroes of a function. They are found algebraically by setting $\begin{aligned} y = 0 \end{aligned}$ and solving for $\begin{aligned} x \end{aligned}$ . Watch the videos below for practice:
::x 界面是函数交叉 x 轴的位置,而函数的高度为零。它们也被称为函数的根、解决方案和零。它们通过设置 y=0 和 x 的解析找到代数。观看下面的视频练习 :

Examples
::实例

Example 1
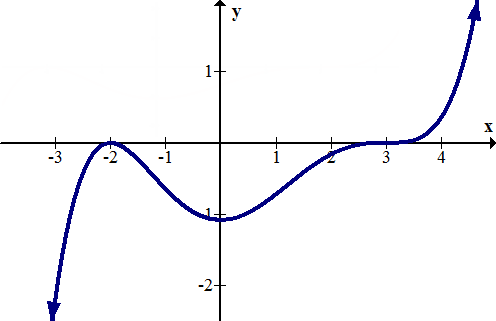
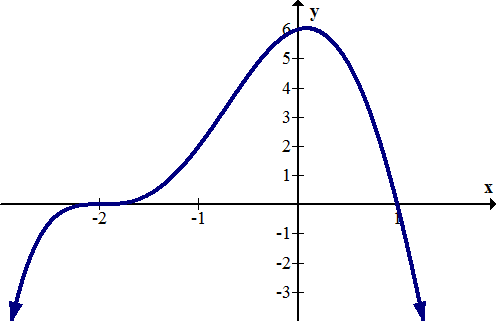
::例1

Earlier, you were asked what the intercepts of the graph below are.
::早些时候,有人问你下图的截取内容是什么。

Graphically the function has zeroes at -2 and 3 with a $\begin{aligned} y \end{aligned}$ intercept at about -1.1.
::图形化函数在 - 2 和 3 上为零, y 拦截在 - 1. 1 左右。

Note: In order for a function to pass the vertical line test , it must only have one $\begin{aligned} y \end{aligned}$ -intercept, but it may have multiple $\begin{aligned} x \end{aligned}$ -intercepts.
::注:函数要通过垂直线测试,只能有一个 Y 接口,但可能有多个 x 接口。

Example 2
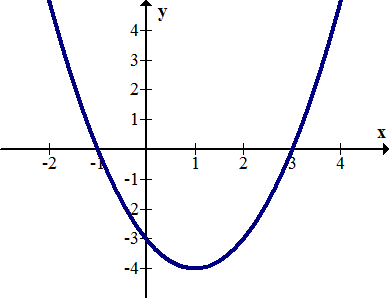
::例2

What are the zeroes and $\begin{aligned} y \end{aligned}$ -intercepts of the parabola $\begin{aligned} y = x^{2} - 2 x - 3 \end{aligned}$ ?
::抛物线 y=x2-2x-3的零和 Y 截面是什么 ?

Using a graph:
::使用图表 :

The zeroes are at (-1, 0) and (3, 0). The $\begin{aligned} y \end{aligned}$ -intercept is at (0, -3).
::零位为(-1,0)和(3,0), Y 拦截为(0,3)。

Using Algebra:
::使用代数 :

Substitute 0 for $\begin{aligned} y \end{aligned}$ to find zeroes.
::替换 0 y 的 y 找到零。

$\begin{aligned} 0 = x^{2} - 2 x - 3 = (x - 3) (x + 1) \end{aligned}$
::0=x2-2-2x-3=(x-3)(x+1)

$\begin{aligned} y = 0, x = 3, - 1 \end{aligned}$
::y=0,x=3,-1

Substitute 0 for $\begin{aligned} x \end{aligned}$ to find the $\begin{aligned} y \end{aligned}$ -intercept.
::X 寻找 Y 接口的代号 0 。

$\begin{aligned} y = (0)^{2} - 2 (0) - 3 = - 3 \end{aligned}$
::y=(0)2-2-2(0)-33

$\begin{aligned} x = 0, y = - 3 \end{aligned}$
::x=0,y3

Example 3
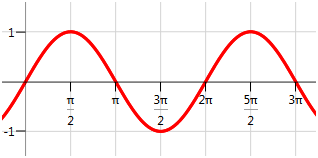
::例3

Identify the zeroes and $\begin{aligned} y \end{aligned}$ -intercepts for the sine function.
::识别正弦函数的零和 Y 界面。

The $\begin{aligned} y \end{aligned}$ -intercept is (0, 0). There are four zeroes visible on this portion of the graph. One thing you know about the sine graph is that it is periodic and repeats forever in both directions. In order to capture every $\begin{aligned} x \end{aligned}$ -intercept, you must identify a pattern instead of trying to write out every single one.
::Y 界面为 0, 0 。图形的这一部分有 4 零可见。关于正弦图, 您知道的一件事是, 它是周期性的, 在两个方向中会永远重复。为了捕捉每个 X 界面, 您必须确定一个模式, 而不是试图写出每一个模式。

The visible $\begin{aligned} x \end{aligned}$ -intercepts are $\begin{aligned} 0, π, 2 π, 3 π \end{aligned}$ . The pattern is that there is an $\begin{aligned} x \end{aligned}$ -intercept every multiple of $\begin{aligned} π \end{aligned}$ including negative multiples. In order to describe all of these values you should write:
::x 的可见界面为 0, , 2, 3. 。模式是 X 拦截包括负倍数的每个 + 的多个。为了描述所有这些值, 您应该写入 :

The $\begin{aligned} x \end{aligned}$ -intercepts are $\begin{aligned} \pm n π \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is an integer $\begin{aligned} {0, \pm 1, \pm 2, \dots} \end{aligned}$ .
::x- 拦截是 n 是整数 { 0, 1, 2,...} 的 nn 。

Example 4
::例4

Identify the intercepts and zeroes of the function: $\begin{aligned} f (x) = \frac{1}{100} (x - 3)^{3} (x + 2)^{2} \end{aligned}$ .
::识别函数( f( x) = 1100( x-3) 33( x+2)) 的拦截和零值。

To find the $\begin{aligned} y \end{aligned}$ -intercept, substitute 0 for $\begin{aligned} x \end{aligned}$ :
::要找到 Y 接口, x 的替代值 0 :

$\begin{aligned} y = \frac{1}{100} (0 - 3)^{3} (0 + 2)^{2} = \frac{1}{100} (- 27) (4) = - \frac{108}{100} = - 1.08 \end{aligned}$
::y=1100(0-3)3(0+2)2=1100(-27)(4)1081001.08

To find the $\begin{aligned} x \end{aligned}$ -intercepts, substitute 0 for $\begin{aligned} y \end{aligned}$ :
::要找到 X 界面, 替换 0 替换 y :

$\begin{aligned} 0 = \frac{1}{100} (x - 3)^{3} (x + 2)^{2} \end{aligned}$
::0=1100(x-3-3)3(x+2)2

$\begin{aligned} x = 3, - 2 \end{aligned}$
::x=3,-2,x=3,-2

Thus the $\begin{aligned} y \end{aligned}$ -intercept is (0, -1.08) and the $\begin{aligned} x \end{aligned}$ -intercepts are (3, 0) and (-2, 0).
::因此,y 界面是 (0, -1.08) , x 界面是 (3, 0) 和 (2, 0) 。

Example 5
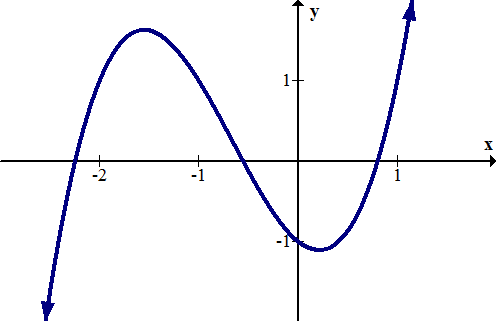
::例5

Determine the intercepts of the following function graphically.
::以图形方式确定以下函数的拦截量。

The $\begin{aligned} y \end{aligned}$ -intercept is approximately (0, -1). The $\begin{aligned} x \end{aligned}$ -intercepts are approximately (-2.3, 0), (-0.4, 0) and (0.7, 0). When finding values graphically, answers are always approximate. Exact answers need to be found analytically.
::y 界面大约为 0, - 1 。 x 界面大约为 (- 2.3, 0, 0, 0, 0) 和 ( 0. 7, 0) 。以图形方式查找值时, 答案总是大致的。精确答案需要用分析方式找到。

Summary

An intercept in mathematics is where a function crosses the x or y axis.
::数学截取是函数横跨 x 或 Y 轴的位置。

y-intercepts are where functions cross the y axis, found algebraically by setting $\begin{aligned} x = 0 \end{aligned}$ and solving for y.
::y 界面是函数横过 y 轴的位置,通过设置 x=0 和 y 的解析找到代数。

x-intercepts are where a function crosses the x axis, found algebraically by setting $\begin{aligned} y = 0 \end{aligned}$ and solving for x.
::x 界面是函数交叉 x 轴的位置,通过设置 y=0 和解析 x 找到代数。

x-intercepts are also called roots, solutions, and zeroes of a function.
::x 界面也称为函数的根、解决办法和零。

Review
::回顾

1. Determine the zeroes and $\begin{aligned} y \end{aligned}$ -intercept of the following function using algebra:
::1. 使用代数确定下列函数的零和Y界面:

$\begin{aligned} f (x) = (x + 1)^{3} (x - 4) \end{aligned}$
:xx) = (x+1) 3(x- 4)

2. Determine the roots and $\begin{aligned} y \end{aligned}$ -intercept of the following function using algebra or a graph:
::2. 使用代数或图表确定下列函数的根和 Y 界面:

$\begin{aligned} g (x) = x^{4} - 2 x^{3} - 7 x^{2} + 20 x - 12 \end{aligned}$
::g(x) =x4- 2x3- 7x2+20x- 12

3. Determine the intercepts of the following function graphically:
::3. 以图形方式确定以下函数的拦截量:

Find the intercepts for each of the following functions.
::查找以下每个函数的拦截功能。

4. $\begin{aligned} y = x^{2} \end{aligned}$
::4. y=x2

5. $\begin{aligned} y = x^{3} \end{aligned}$
::5. y=x3

6. $\begin{aligned} y = \ln (x) \end{aligned}$
::6.y=ln(x)

7. $\begin{aligned} y = \frac{1}{x} \end{aligned}$
::7.y=1x

8. $\begin{aligned} y = e^{x} \end{aligned}$
::8. y=ex

9. $\begin{aligned} y = \sqrt{x} \end{aligned}$
::9.y=x 9y=x

10. Are there any functions without a $\begin{aligned} y \end{aligned}$ -intercept? Explain.
::10. 是否有任何功能没有y-intermissions?解释。

11. Are there any functions without an $\begin{aligned} x \end{aligned}$ -intercept? Explain.
::11. 是否有任何功能没有 X 拦截?解释。

12. Explain why it makes sense that an $\begin{aligned} x \end{aligned}$ -intercept of a function is also called a “zero” of the function.
::12. 解释为什么一个函数的X拦截也称为函数的 " 零 " 是有道理的。

Determine the intercepts of the following functions using algebra or a graph.
::使用代数或图表确定以下函数的拦截量。

13. $\begin{aligned} h (x) = x^{3} - 6 x^{2} + 3 x + 10 \end{aligned}$
::13. h(x) =x3 - 6x2+3x+10

14. $\begin{aligned} j (x) = x^{2} - 6 x - 7 \end{aligned}$
::14. j(x)=x2-6x-7

15. $\begin{aligned} k (x) = 4 x^{4} - 20 x^{3} - 3 x^{2} + 14 x + 5 \end{aligned}$
::15. kk(x)=4x4-20x3-3-3x2+14x+5

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

零职能和零职能拦截

X and Y Intercepts ::X Y 和 X Y 拦截器

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)