课程： 1.11 职能构成 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

职能构成构成

Functions can be added, subtracted, multiplied and divided creating new functions and graphs that are complicated combinations of the various original functions. One important way to transform functions is through function composition. Function composition allows you to line up two or more functions that act on an input in tandem.
::函数可以添加、减减、乘和分割,创建新的函数和图表,这些功能和图表是各种原始函数的复杂组合。转换函数的一个重要途径是通过函数构成。函数构成允许您排列两个或两个以上的函数,这些函数对输入同步发挥作用。

Is function composition essentially the same as multiplying the two functions together?
::函数构成是否基本上与将两个函数相乘相同?

Composition of Functions
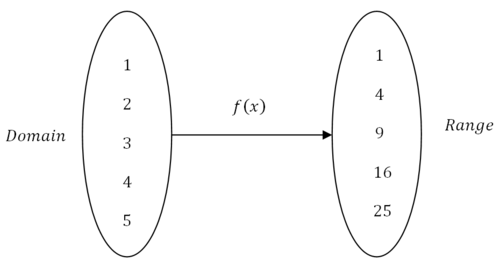
::职能的组成

A common way to describe functions is a mapping from the domain space to the range space:
::描述函数的一种常见方式是绘制从域空间到范围空间的地图:

Function composition means that you have two or more functions and the range of the first function becomes the domain of the second function.
::函数构成是指您有两个或两个以上函数,而第一个函数的范围成为第二个函数的域。

There are two notations used to describe function composition. In each case the order of the functions matters because arithmetically the outcomes will be different. Squaring a number and then doubling the result will be different from doubling a number and then squaring the result. In the diagram above, $\begin{aligned} f (x) \end{aligned}$ occurs first and $\begin{aligned} g (x) \end{aligned}$ occurs second. This can be written as:
::用于描述函数构成有两个符号。在每种情况下,函数的顺序都很重要, 因为从算术上看结果会不同。将一个数字对齐, 然后将结果翻一番, 然后将结果对齐, 而不是将数字翻一番, 然后将结果对齐。在以上图表中, f( x) 发生于第一个, g( x) 发生于第二个。这可以写为 :

$\begin{aligned} g (f (x)) \end{aligned}$ or $\begin{aligned} (g \circ f) (x) \end{aligned}$
::g(f(x)) 或 (gf(x)

You should read this “ $\begin{aligned} g \end{aligned}$ of $\begin{aligned} f \end{aligned}$ of $\begin{aligned} x \end{aligned}$ .” In both cases notice that the $\begin{aligned} f \end{aligned}$ is closer to the $\begin{aligned} x \end{aligned}$ and operates on the $\begin{aligned} x \end{aligned}$ values first.
::您应该读取“ x 的 g ” 。在这两种情况下,您都注意 f 更接近 x , 并首先使用 x 值操作。

Examples
::实例

Example 1
::例1

Earlier, you were asked if function composition is the same as multiplying two functions together. Function composition is not the same as multiplying two functions together. With function composition there is an outside function and an inside function. Suppose the two functions were doubling and squaring. It is clear just by looking at the example input of the number 5 that 50 (squaring then doubling) is different from 100 (doubling then squaring). Both 50 and 100 are examples of function composition, while 250 (five doubled multiplied by five squared) is an example of the product of two separate functions happening simultaneously.
::早些时候, 有人询问函数构成是否与将两个函数相乘相同。函数组成与将两个函数相乘不同。函数组成与将两个函数相乘不同。有函数组成存在外部函数和一个内部函数。假设这两个函数是双倍和对齐的。显而易见, 仅仅通过查看第 5 个函数的示例输入, 50 个( 相形之下翻倍) 和 100个( 相形之下翻倍 ) 不同。 50 个和 100 个是功能组成的例子, 而 250 个( 5 倍乘以 5 平方) 是同时发生的两个单独函数的产物。

For the next two examples, use the functions below:
::对于下面两个例子,请使用以下功能:

$\begin{aligned} f (x) = x^{2} - 1 \end{aligned}$
:xx)=x2-1

$\begin{aligned} h (x) = \frac{x - 1}{x + 5} \end{aligned}$
::h(x) =x - 1x+5

$\begin{aligned} g (x) = 3 e^{x} - x \end{aligned}$
::g( x) = 3ex- x

$\begin{aligned} j (x) = \sqrt{x + 1} \end{aligned}$
::j(x)=x+1

Example 3
::例3

Show $\begin{aligned} f (h (x)) \neq h (f (x)) \end{aligned}$
::显示 f( h(x)) @ h(f(x))

$\begin{aligned} f (h (x)) = f (\frac{x - 1}{x + 5}) = {(\frac{x - 1}{x + 5})}^{2} - 1 \end{aligned}$
::f(h(x)) = f(x-1x+5) = (x-1x+5) = (x-1x+5) 2-1

$\begin{aligned} h (f (x)) = h (x^{2} - 1) = \frac{(x^{2} - 1) - 1}{(x^{2} - 1) + 5} = \frac{x^{2} - 2}{x^{2} + 4} \end{aligned}$
::h(f(xx))=h(x2-1)=(x2-1)=(x2-1)-1-1(x2-1)-1(x2-1)+5=x2-2x2+4

In order to truly show they are not equal it is best to find a specific counter example of a number where they differ. Sometimes algebraic expressions may look different, but are actually the same. You should notice that $\begin{aligned} f (h (x)) \end{aligned}$ is undefined when $\begin{aligned} x = - 5 \end{aligned}$ because then there would be zero in the denominator. $\begin{aligned} h (f (x)) \end{aligned}$ on the other hand is defined at $\begin{aligned} x = - 5 \end{aligned}$ . Since the two function compositions differ, you can conclude:
::要真正显示它们不相等, 最好找到一个不同的数字的具体对应示例。有时代数表达式可能看起来不同, 但实际上是一样的。您应该注意, f( h( x)) 在 x% 5 时没有定义, 因为那样的话分母中就会为零。 h( f( x)) 在 x% 5 时定义了。由于两种函数的构成不同, 您可以得出结论 :

$\begin{aligned} f (h (x)) \neq h (f (x)) \end{aligned}$
::f(h(xx)) h(f(x))

Example 4
::例4

What is $\begin{aligned} f (j (h (g (x)))) \end{aligned}$ ?
::什么是f(j(g(x)))?

These functions are nested within the arguments of the other functions. Sometimes functions simplify significantly when composed together, as $\begin{aligned} f \end{aligned}$ and $\begin{aligned} j \end{aligned}$ do in this case. It makes sense to evaluate those two functions first together and keep them on the outside of the argument.
::这些功能被嵌套在其他函数的参数中。有时这些功能在组合时会大大简化, 在本案中, f 和 j 一样。首先评价这两个函数, 并把它们放在参数之外是有道理的。

$\begin{aligned} f (x) = x^{2} - 1; h (x) = \frac{x - 1}{x + 5}; g (x) = 3 e^{x} - x; j (x) = \sqrt{x + 1} \end{aligned}$
:x) =x2 - 1;h(x) =x - 1x+5;g(x) = 3ex - x;j(x) =x+1

%20%5Cbig)%20%3D%20f%20%5Cleft%20(%20%5Csqrt%7By%20%2B%201%7D%20%5Cright%20)%20%20%3D%20%5Cleft%20(%20%5Csqrt%7By%20%2B%201%7D%20%5Cright%20)%20%5E2%20-%201%20%3D%20y%20%2B%201%20-%201%20%3D%20y"> $\begin{aligned} f (j (y)) = f (\sqrt{y + 1}) = {(\sqrt{y + 1})}^{2} - 1 = y + 1 - 1 = y \end{aligned}$
::f( j) = f(y+1) = (y+1) = (y+1) 2 - 1=y+1 - 1=y

Notice how the composition of $\begin{aligned} f \end{aligned}$ and $\begin{aligned} j \end{aligned}$ produced just the argument itself?
::注意到F和j的构成如何仅产生论据本身?

Thus,
::因此,

\begin{aligned} f (j (h (g (x)))) = h (g (x)) & = h (3 e^{x} - x) \\ = \frac{(3 e^{x} - x) - 1}{(3 e^{x} - x) + 5} \\ = \frac{3 e^{x} - x - 1}{3 e^{x} - x + 5} \end{aligned}

j(h(g(x)))=h(g(x))=h(3ex-x)=(3ex-x)=(3ex-x)-1(3ex-x)+5=3ex-x)=3x-13ex-x+5

For the next two examples, use the graphs shown below:
::对于下面两个例子,请使用以下图表:

$\begin{aligned} f (x) = | x | \end{aligned}$
:fx)

$\begin{aligned} g (x) = e^{x} \end{aligned}$
::g(x) =ex

$\begin{aligned} h (x) = - x \end{aligned}$
:hx) x

Example 4
::例4

Compose $\begin{aligned} g (f (x)) \end{aligned}$ and graph the result. Describe the transformation.
::g(f(x)) 和图形结果。描述转换。

$\begin{aligned} g (f (x)) = g (| x |) = e^{| x |} \end{aligned}$
::g( f( x)) = g( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ g( f( x) ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

The positive portion of the exponential graph has been mirrored over the $\begin{aligned} y \end{aligned}$ axis and the negative portion of the exponential graph has been entirely truncated.
::指数图正数部分已反射到 y 轴上,指数图负数部分已完全缩短。

Example 5
::例5

Compose $\begin{aligned} h (g (x)) \end{aligned}$ and graph the result. Describe the transformation.
::撰写 h( g( x) ) 并绘制结果图。描述转换。

$\begin{aligned} h (g (x)) = h (e^{x}) = - e^{x} \end{aligned}$
::h( g( x) ) =h( ex) \\ ex

The exponential graph has been reflected over the $\begin{aligned} x \end{aligned}$ -axis.
::指数图已经反射到 X 轴上。

Summary

Function composition involves lining up two or more functions that go one after another. The range of one function becomes the domain for the next.
::函数构成包括排列两个或两个以上相互交错的函数。一个函数的范围成为下一个函数的域。

For example, a composition of functions $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ could look like: $\begin{aligned} g (f (x)) \end{aligned}$ or $\begin{aligned} (g \circ f) (x) . \end{aligned}$
::例如,函数f(x)和g(x)的构成可能看起来像:g(f(x))或(gf(x)。

The order of functions in composition matters, as different outcomes can be achieved depending on the sequence.
::组成事项的职能顺序,因为根据顺序可以取得不同的结果。

Review
::回顾

For questions 1-9, use the following three functions: $\begin{aligned} f (x) = | x |, h (x) = - x, g (x) = (x - 2)^{2} - 3 \end{aligned}$ .
::对于问题1-9,使用以下三个函数:f(x)xx,h(x)x,g(x)=(x-2)2-3。

1. Graph $\begin{aligned} f (x), h (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ .
::1. 图f(x)、h(x)和g(x)。

2. Find $\begin{aligned} f (g (x)) \end{aligned}$ algebraically.
::2. 查找f(g(x))代数。

3. Graph $\begin{aligned} f (g (x)) \end{aligned}$ and describe the transformation.
::3. 图f(g(x))和说明变换情况。

4. Find $\begin{aligned} g (f (x)) \end{aligned}$ algebraically.
::4. 查找 g(f(x)) 代数。

5. Graph $\begin{aligned} g (f (x)) \end{aligned}$ and describe the transformation.
::5. 图g(f(x))和说明变换情况。

6. Find $\begin{aligned} h (g (x)) \end{aligned}$ algebraically.
::6. 查找h(g(x))代数。

7. Graph $\begin{aligned} h (g (x)) \end{aligned}$ and describe the transformation.
::7. 图h(g(x))并说明变换情况。

8. Find $\begin{aligned} g (h (x)) \end{aligned}$ algebraically.
::8. 查找 g(h(x))代数。

9. Graph $\begin{aligned} g (h (x)) \end{aligned}$ and describe the transformation.
::9. 图g(h(x))和说明变换情况。

For 10-16, use the following three functions: $\begin{aligned} j (x) = x^{2}, k (x) = | x |, m (x) = \sqrt{x} \end{aligned}$ .
::对于 10-16, 使用以下三个函数 : j( x) =x2, k( x) x , m( x) =x。

10. Graph $\begin{aligned} j (x), k (x) \end{aligned}$ and $\begin{aligned} m (x) \end{aligned}$ .
::10. 图j(x),k(x)和m(x).

11. Find $\begin{aligned} j (k (x)) \end{aligned}$ algebraically.
::11. 查找j(k(x))代数。

12. Graph $\begin{aligned} j (k (x)) \end{aligned}$ and describe the transformation.
::12. 图j(k(x)),说明变换情况。

13. Find $\begin{aligned} k (m (x)) \end{aligned}$ algebraically.
::13. 查找 k(m(xx)) 代数。

14. Graph $\begin{aligned} k (m (x)) \end{aligned}$ and describe the transformation.
::14. 图k(m(x))和说明变换情况。

15. Find $\begin{aligned} m (k (x)) \end{aligned}$ algebraically.
::15. 查找 m(k(x)) 代数。

16. Graph $\begin{aligned} m (k (x)) \end{aligned}$ and describe the transformation.
::16. 图m(k(x))和说明变换情况。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

职能构成构成

Composition of Functions ::职能的组成

Examples ::实例

Example 1 ::例1

Example 3 ::例3

Example 4 ::例4

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Composition of Functions
::职能的组成

Examples
::实例

Example 1
::例1

Example 3
::例3

Example 4
::例4

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)