课程： 2.10 水平单数 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

水平单数

Vertical asymptotes describe the behavior of a function as the values of $\begin{aligned} x \end{aligned}$ approach a specific number. Horizontal asymptotes describe the behavior of a function as the values of $\begin{aligned} x \end{aligned}$ become infinitely large and infinitely small. Since functions cannot touch vertical asymptotes, are they not allowed to touch horizontal asymptotes either?
::垂直 asymptotes 描述函数的行为为 x 方位数的值。水平 asymptotes 描述函数的行为为 x becomm 无限大和无限小的值。由于函数无法触动垂直的 asymptotes, 它们是否也不允许触动水平的 asymptotes ?

Finding Horizontal Asymptotes
::查找水平单数

Horizontal asymptotes are a means of describing end behavior of a function. End behavior essentially is a description of what happens on either side of the graph as the function continues to the right and left infinitely. When you are determining the horizontal asymptotes, it is important to consider both the right and the left hand sides, because the horizontal asymptotes will not necessarily be the same in both places. Consider the reciprocal function and note how as $\begin{aligned} x \end{aligned}$ goes to the right and left it flattens to the line $\begin{aligned} y = 0 \end{aligned}$ .
::水平向量是描述函数结束行为的一种方式。结束行为本质上是描述图形两侧随函数向右和向左持续而发生的情况。当确定水平向量时, 必须考虑到左和右两侧, 因为水平向量在两个地方不一定都是一样的。考虑对等函数, 并注意 x 如何向右和向左倾斜到 y=0 线。

Sometimes functions flatten out and other times functions increase or decrease without bound. There are basically three cases.
::有时功能平坦,有时功能增减,有时功能无约束地增减。基本上有三种情况。

Case 1: Degree of Numerator is Less than Degree of Denominator
::案例1: 数值度小于数值度

The first case is the function flattens out to 0 as $\begin{aligned} x \end{aligned}$ gets infinitely large or infinitely small. This happens when the degree of the numerator is less than the degree of the denominator. The degree is determined by the greatest exponent of $\begin{aligned} x \end{aligned}$ .
::第一种情况是当 x 变得无限大或无限小时,函数平坦到 0。当分子的程度小于分母的程度时,就会发生这种情况。度由 x 的最大出处决定。

\begin{aligned} f (x) = \frac{2 x^{8} + 3 x^{2} + 100}{x^{9} - 12} \end{aligned}

x) = 2x8+3x2+100x9- 12

One way to reason through why this makes sense is because when $\begin{aligned} x \end{aligned}$ is a ridiculously large number then most parts of the function hardly make any impact. The 100 for example is nothing in comparison and neither is the $\begin{aligned} 3 x^{2} \end{aligned}$ . The two important terms to compare are $\begin{aligned} x^{8} \end{aligned}$ and $\begin{aligned} x^{9} \end{aligned}$ . The 2 isn’t even important now because if $\begin{aligned} x \end{aligned}$ is even just a million than the $\begin{aligned} x^{9} \end{aligned}$ will be a million times bigger than the $\begin{aligned} x^{8} \end{aligned}$ and the 2 hardly matters again. Essentially, when $\begin{aligned} x \end{aligned}$ gets big enough, this function acts like $\begin{aligned} \frac{1}{x} \end{aligned}$ which has a horizontal asymptote of 0.
::解释为什么这有道理的一个方法就是,当x是一个荒谬的庞大数字时,函数的大多数部分几乎不会产生任何影响。比如,100个函数与3x2相比都算不上什么,而3x2也算不上。比较的两个重要术语是 x8 和 x9 。现在,2个术语甚至都不重要,因为如果x甚至只是一百万比x9,那么,如果x甚至比x9大一百万倍,则比x8大一百万倍,而2个函数就几乎不再重要了。基本上,当x变得足够大的时候,这个函数就像1x一样,它具有0的横向分数。

Case 2: Degree of Numerator is Equal to the Degree of Denominator
::案例2: 数值度等于指数度

If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is equal to the ratio of the leading coefficients.
::如果分子的程度等于分母的程度,则水平零点等于主要系数的比率。

\begin{aligned} f (x) = \frac{6 x^{4} - 3 x^{3} + 12 x^{2} - 9}{3 x^{4} + 144 x - 0.001} \end{aligned}

x)=6x4-3x3+12x2-93x4+144x-0.001

Notice how the degree of both the numerator and the denominator is 4. This means that the horizontal asymptote is $\begin{aligned} y = \frac{6}{3} = 2 \end{aligned}$ . One way to reason through why this makes sense is because when $\begin{aligned} x \end{aligned}$ gets to be a very large number all the smaller powers will not really make much of an impact. The biggest contributors are only the biggest powers. Then the value of the numerator will be about twice that of the denominator. As $\begin{aligned} x \end{aligned}$ gets even bigger, then the function will get even closer to 2.
::注意分子和分母的程度是 4 。这意味着水平的零点为 y=63=2 。解释为什么这个道理的一个方法就是, 当 x 变成一个非常大的数量时, 所有较小的力量都不会真正产生很大的影响。最大的贡献者只是最大的力量。然后, 分子的价值将是分母的两倍左右。当 x 变大时, 函数就会更接近于 2 。

Case 3 : Degree of Numerator is Greater than the Degree of Denominator
::案例3: 数值度大于数值度

If the degree of the numerator is greater than the degree of the denominator, there does not exist a horizontal asymptote. You must determine if the function increases or decreases without bound in both the left and right directions.
::如果分子的大小大于分母的分母的分母大小,则不存在水平的静态。您必须确定函数的增减是否不附带左右方向。

Watch the following video, focusing on the parts about horizontal asymptotes.
::关注下一段视频, 关注关于水平微粒的部分。

Examples
::实例

Example 1
::例1

Earlier, you were asked if functions are allowed to touch their horizontal asymptotes. Functions may touch and pass through horizontal asymptotes without limit. This is a difference between vertical and horizontal asymptotes. In calculus, there are rigorous proofs to show that functions like the one in Example C do become arbitrarily close to the asymptote.
::早些时候,有人询问是否允许函数触摸其水平静态。函数可以不受限制地触摸和通过水平静态。这是垂直和水平静态的区别。在微积分中, 有严格的证据表明, 例C 中的函数确实任意地接近静态。

Example 2
::例2

Identify the vertical and horizontal asymptotes of the following rational function .
::识别以下合理函数的垂直和水平小数。

\begin{aligned} f (x) = \frac{(x - 2) (4 x + 3) (x - 4)}{(x - 1) (4 x + 3) (x - 6)} \end{aligned}

x) = (x-2)(4x+3)(x-4)(x-1)(4x+3)(x-6)

There is factor that cancels that is neither a horizontal or vertical asymptote . The vertical asymptotes occur at $\begin{aligned} x = 1 \end{aligned}$ and $\begin{aligned} x = 6 \end{aligned}$ . To obtain the horizontal asymptote you could methodically multiply out each binomial , however since most of those terms do not matter, it is more efficient to first determine the relative powers of the numerator and the denominator. In this case they both happen to be 3. Next determine the coefficient of the cubic terms only. The numerator will have $\begin{aligned} 4 x^{3} \end{aligned}$ and the denominator will have $\begin{aligned} 4 x^{3} \end{aligned}$ and so the horizontal asymptote will occur at $\begin{aligned} y = \frac{4}{4} = 1 \end{aligned}$ .
::取消的系数既不是水平或垂直的单点。垂直的单点在 x=1 和 x=6 时发生。垂直的单点在 x=1 和 x=6 时发生。要获得水平的单点, 您可以有条不紊地乘出每个二点形, 但是由于大多数这两个词都无关紧要, 首先确定分子和分母的相对功率比较有效。在此情况下, 它们碰巧是 3 。下一步只确定立方条件的系数。分子将拥有 4x3 , 分母将拥有 4x3 , 所以水平的单点将在 y=44=1 时发生。

Example 3
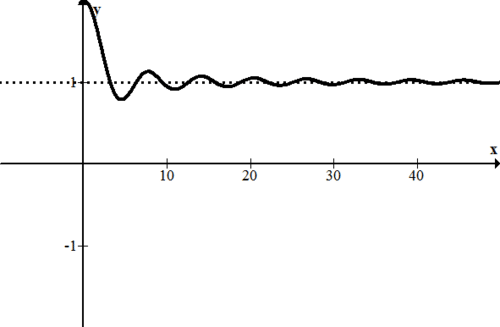
::例3

Describe the right hand end behavior of the following function.
::描述以下函数的右手端行为。

Notice how quickly this dampening wave function settles down. There seems to be an obvious horizontal axis on the right at $\begin{aligned} y = 1 \end{aligned}$
::注意这个降压波函数如何迅速稳定下来。 y=1 右侧似乎有一个明显的水平轴

Example 4
::例4

Identify the horizontal asymptotes of the following function.
::识别以下函数的水平小数点。

\begin{aligned} f (x) = \frac{(x - 3) (x + 2)}{| (x - 5) | \cdot (x - 1)} \end{aligned}

xx) = (x-3) (x+2) (x-5) (x-1)

First notice the absolute value surrounding one of the terms in the denominator. The degrees of both the numerator and the denominator will be 2 which means that the horizontal asymptote will occur at a number. As $\begin{aligned} x \end{aligned}$ gets infinitely large, the function is approximately:
::首先注意分母中一个术语的绝对值。分子和分母的度为 2, 这意味着水平的同位数将出现在一个数字上。当 x 变得无限大时, 该函数大约为 :

\begin{aligned} f (x) = \frac{x^{2}}{x^{2}} \end{aligned}

xx) =x2x2

So the horizontal asymptote is $\begin{aligned} y = - 1 \end{aligned}$ as $\begin{aligned} x \end{aligned}$ gets infinitely large.
::所以水平渐渐消逝是 y1, 因为 x 会变得无限大。

On the other hand, as $\begin{aligned} x \end{aligned}$ gets infinitely small the function is approximately:
::另一方面,当x变得无限小时,函数大约为:

\begin{aligned} f (x) = \frac{x^{2}}{- x^{2}} \end{aligned}

xx) =x2 -x2

So the horizontal asymptote is $\begin{aligned} y = - 1 \end{aligned}$ as $\begin{aligned} x \end{aligned}$ gets infinitely small.
::所以水平渐渐消逝是 y1, 因为 x 变得无限小。

In this case, you cannot blindly use the leading coefficient rule because the absolute value changes the sign.
::在这种情况下,你不能盲目使用主要系数规则,因为绝对值会改变符号。

Example 5
::例5

Identify the horizontal asymptotes if they exist for the following 3 functions.
::如果存在以下3个函数,则标明水平小数点。

$\begin{aligned} f (x) = \frac{3 x^{6} - 72 x}{x^{6} + 999} \end{aligned}$
::f(x)=3x6-72x26+999

The degrees of the numerator and the denominatro are equal so the horizontal asymptote is $\begin{aligned} y = 3 \end{aligned}$ .
::分子和离子体的度相等,所以水平的静态等离子体=3。

$\begin{aligned} h (x) = \frac{a x^{4} + b x^{3} + c x^{2} + d x + e}{f x^{4} + g x^{3} + h x^{2}} \end{aligned}$
::h(x) = 轴4+bx3+cx2+dx+efx4+gx3+hx2

The degrees of the numerator and the denominator are equal again so the horizontal asymptote is $\begin{aligned} y = \frac{a}{f} \end{aligned}$
::分子和分母的度数和分母再次等同,所以水平渐微是 y=af

$\begin{aligned} g (x) = \frac{f (x)}{h (x)} \end{aligned}$
:x)=f(x)h(x)

As $\begin{aligned} x \end{aligned}$ gets infinitely large,
::当x变得无限大,

\begin{aligned} g (x) = \frac{f (x)}{h (x)} = \frac{\frac{3 x^{6} - 72 x}{x^{6} + 999}}{\frac{a x^{4} + b x^{3} + c x^{2} + d x + e}{f x^{4} + g x^{3} + h x^{2}}} \approx \frac{3}{\frac{a}{f}} = \frac{3 f}{a} \end{aligned}

::g(x) = f(x) = 3x6 - 72x26+ 999ax4+bx3+cx2+dx+efx4+gx3+hx2=3af=3fa

When you study calculus, you will learn the rigorous techniques that enable you to feel more confident about results like this.
::当你学习微积分时, 你会学习严格的技巧使你对这样的结果更有信心。

Summary

Horizontal asymptotes describe the end behavior of a function as the values become infinitely large or small.
::当值变得无限大或小时,水平等量表示函数的最终行为。

There are three cases to consider when finding horizontal asymptotes
- Case 1: If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
  ::案例1:如果分子的程度小于分母的程度,则水平零位数为y=0。
- Case 2: If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is equal to the ratio of the leading coefficients.
  ::案例2:如果分子的程度等于分母的程度,则水平零点等于主要系数的比率。
- Case 3: If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
  ::案例3:如果分子的程度大于分母的程度,就不会有横向的零星现象。
::案例1:如果分子的程度小于分母的程度,则水平的同位数为y=0。案例2:如果分子的程度等于分母的程度,则水平的同位数等于主要系数的比率。案例3:如果分子的程度大于分母的程度,则没有水平的同位数。

Review
::回顾

Identify the horizontal asymptotes, if they exist, for the following functions.
::标明下列函数的横向小数点(如果存在的话)。

$\begin{aligned} f (x) = \frac{5 x^{4} - 2 x}{x^{4} + 32} \end{aligned}$
:xx)=5x4-2x24+32

$\begin{aligned} g (x) = \frac{3 x^{4} - 2 x^{6}}{- x^{4} + 2} \end{aligned}$
::g(x) = 3x4 - 2x6 - x4+2

$\begin{aligned} h (x) = \frac{3 x^{4} - 5 x}{8 x^{3} + 3 x^{4}} \end{aligned}$
::h(x) = 3x4 - 5x8x3+3x4

$\begin{aligned} j (x) = \frac{2 x^{3} - 15 x}{- x^{4} + 3} \end{aligned}$
::j(x) = 2x3 - 15x - x4+3

$\begin{aligned} k (x) = \frac{2 x^{5} - 3 x}{5 x^{2} + 3 x^{4} + 2 x - 7 x^{5}} \end{aligned}$
:x) = 2x5 - 3x5x2+3x4+2x-7x5

$\begin{aligned} f (x) = \frac{a x^{14} + b x^{23} + c x^{12} + d x + e}{f x^{24} + g x^{23} + h x^{21}} \end{aligned}$
::f(x) = 轴14+bx23+cx12+dx+efx24+gx23+hx21

$\begin{aligned} g (x) = \frac{(x - 1) (x + 4)}{| (x - 2) | \cdot (x - 1)} \end{aligned}$
::g(x) = (x- 1) (x+4) (x-2) (x-2) (x-1)

Write a function that fits the following criteria:
- Vertical asymptotes at $\begin{aligned} x = 1 \end{aligned}$ and $\begin{aligned} x = 4 \end{aligned}$
  ::x=1 和 x=4 时的垂直星数
- Zeroes at 3 and 5
  ::3和5时为零
- Hole when $\begin{aligned} x = 6 \end{aligned}$
  ::x=6 时空空洞
- Horizontal asymptote at $\begin{aligned} y = \frac{2}{3} \end{aligned}$
  ::Y=23 时水平等同
::写入符合以下标准的函数: x=1 和 x=4 的垂直静脉托; 3 和 5 的垂直静脉托; y=23 的 x=6 水平静脉托; 3 和 5 的垂直静脉托; 5 的空洞; y=23 的垂直静脉托; y=6 的垂直静脉托; y=23 的垂直静脉托; y=23 的垂直静脉托; 3 和 5 的垂直空洞; x=6 的横向静脉托; y=23

Write a function that fits the following criteria:
- Vertical asymptotes at $\begin{aligned} x = - 2 \end{aligned}$ and $\begin{aligned} x = 2 \end{aligned}$
  ::x @% 2 和 x=2 的垂直等量
- Zeroes at 1 and 5
  ::1和5时为零
- Hole when $\begin{aligned} x = 3 \end{aligned}$
  ::x=3 时空洞
- Horizontal asymptote at $\begin{aligned} y = 1 \end{aligned}$
  ::Y=1 时水平等同
::写入符合以下标准的函数: x2 和 x=2 的垂直静态, 1 和 5 的零点为 1 和 5 当 x=3 的 Y=1 时, x=2 和 x=2 的垂直静态, y=1 的水平静态

Write a function that fits the following criteria:
- Vertical asymptotes at $\begin{aligned} x = 0 \end{aligned}$ and $\begin{aligned} x = 3 \end{aligned}$
  ::x=0 和 x=3 时的垂直静量
- Zeroes at 1 and 2
  ::1和2时为零
- Hole when $\begin{aligned} x = 8 \end{aligned}$
  ::x=8 时空空洞
- Horizontal asymptote at $\begin{aligned} y = 2 \end{aligned}$
  ::Y=2 时水平等同
::写入符合以下标准的函数 : x=0 和 x=3 0 的垂直静态数。当 x=8 y=2 时, x=3 0 和 2 空洞时, x=8 水平静态数。

Write a function that fits the following criteria:
- Vertical asymptotes at 2 and 6
  ::2 和 6 2 和 6 的垂直空数
- Zero at 5
  ::5时零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零五零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零零
- Hole when $\begin{aligned} x = 4 \end{aligned}$
  ::x=4 时空洞
- Horizontal asymptote at $\begin{aligned} y = 0 \end{aligned}$
  ::y=0 时水平等同
::写入符合以下标准的函数: 当 x=4 y=0 时, 2 和 6 零点为 5 洞时, 2 和 6 的垂直空位数; y=0 时, x=4 水平空位数

Write a function that fits the following criteria:
- Vertical asymptote at 4
  ::4 时垂直为空
- Zeroes at 0 and 3
  ::0和3时为零零
- Hole at when $\begin{aligned} x = 5 \end{aligned}$
  ::x=5 时空时空洞
- No horizontal asymptotes
  ::没有水平的单点数
::写入符合以下标准的函数: 4 0 和 3 洞时为 0 和 0 时为 4 零和 3 洞时为 4 的垂直静态, 当 x= 5 无水平静态

Identify the vertical and horizontal asymptotes of the following rational functions.
::识别以下合理函数的垂直和水平小数。

$\begin{aligned} f (x) = \frac{(x - 5) (2 x + 1) (x - 3)}{(x - 3) (4 x + 5) (x - 6)} \end{aligned}$
:xx) = (x-5)(2x+1)(x-3)(x-3)(x-3)(4x+5)(x-6)

$\begin{aligned} g (x) = \frac{x (x - 1) (x + 3) (x - 5)}{3 x (x - 1) (4 x + 3)} \end{aligned}$
::g(x) =x(x-1)(x+3)(x-5)(x-5)3x(x-1)(4x+3)

$\begin{aligned} h (x) = \frac{(x - 2) (x + 3) (x - 6)}{(x - 4) (x + 3)^{2} (x + 2)} \end{aligned}$
::h(x) = (x- 2) (x+3) (x-6) (x- 4) (x+3) (x+2) (x+2)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

水平单数

Finding Horizontal Asymptotes ::查找水平单数

Case 1: Degree of Numerator is Less than Degree of Denominator ::案例1: 数值度小于数值度

Case 2: Degree of Numerator is Equal to the Degree of Denominator ::案例2: 数值度等于指数度

Case 3 : Degree of Numerator is Greater than the Degree of Denominator ::案例3: 数值度大于数值度

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)