6.2 毕达哥里地名

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 毕达哥里地名

  Collapse Expand

  毕达哥里地名

  播放段落

  The works on right triangles.  If you consider the  $\begin{array}{r}x\end{array}$ coordinate of a point along the unit circle to be the cosine and the  $\begin{array}{r}y\end{array}$ coordinate of the point to be the sine and the distance to the origin to be 1 then the Pythagorean Theorem immediately yields the identity : 
  ::右三角形上的工程。 如果您认为单位圆一端点的x坐标是正弦和圆形坐标是点的正弦, 与起源的距离是 1, 那么Pythagorean 理论立即产生身份 :

  播放段落

  $$\begin{array}{rl}& y^2+x^2=1\\ & {\sin }^{2}x+{\cos }^{2}x=1\end{array}$$

  
  ::y2+x2=1sin2x+cos2x=1

  播放段落

  An observant student may guess that other Pythagorean identities exist with the rest of the trigonometric functions .  Is  $\begin{array}{r}{\tan }^{2}x+{\cot }^{2}x=1\end{array}$ a legitimate identity? 
  ::观察学生可能会猜测其他的毕达哥里身份与其他三角函数存在。 tan2x+cot2x=1是否合法身份?

  播放段落

  Pythagorean Identities 
  ::毕达哥里地名

  播放段落

  The proof of the Pythagorean identity for is essentially just drawing a right triangle in a unit circle, identifying the cosine as the  $\begin{array}{r}x\end{array}$ coordinate, the sine as the  $\begin{array}{r}y\end{array}$ coordinate and 1 as the hypotenuse.
  ::Pytagorean 身份的证明基本上是在单位圆中绘制右三角形,将余弦作为x坐标,正弦作为Y坐标,1作为下限。

  

  播放段落

  $\begin{array}{r}{\cos }^{2}x+{\sin }^{2}x=1\end{array}$
  ::cos2x+sin2x=1

  播放段落

  or
  ::或

  播放段落

  $\begin{array}{r}{\sin }^{2}x+{\cos }^{2}x=1\end{array}$
  ::sin2\\ x x+cos2\\\\ x=1

  播放段落

  The two other Pythagorean identities are:
  ::另外两个毕达哥里人的身份是:

  播放段落
  • $\begin{array}{r}1+{\cot }^{2}x={\csc }^{2}x\end{array}$
    ::1+cot2x=csc2x
  播放段落
  • $\begin{array}{r}{\tan }^{2}x+1={\sec }^{2}x\end{array}$
    ::tan2+1=sec2}*xx==sec2}*x

  播放段落

  To derive these two Pythagorean identities, divide the original Pythagorean identity by $\begin{array}{r}{\sin }^{2}x\end{array}$  and $\begin{array}{r}{\cos }^{2}x\end{array}$  respectively.
  ::为了获得这两个毕达哥里人的身份,将原毕达哥里人的身份分别用sin2x和cos2x分开。

  播放段落

  To derive the Pythagorean identity  $\begin{array}{r}1+{\cot }^{2}x={\csc }^{2}x\end{array}$  divide through by $\begin{array}{r}{\sin }^{2}x\end{array}$  and simplify.
  ::得出 Pythagoren 身份 1+cot2x=csc2x 通过 sin2x 和简化分隔 。

  播放段落

  $$\begin{array}{rl}\frac{{\sin }^{2}x}{{\sin }^{2}x}+\frac{{\cos }^{2}x}{{\sin }^{2}x}& =\frac{1}{{\sin }^{2}x}\\ 1+{\cot }^{2}x& ={\csc }^{2}x\end{array}$$

  
  ::=1sin2=1sin2=1x1+cot2=xx=csc2=xxxxxxxxxx=csc2=xxxxxxxxxxin2=1sin2=xxxx1+ct2=xxxxxxxxxxcsc2}xxx=csc2}xx=xxxxxin2_xxxxxxxxxxxxxxxxxxin2xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxin2xxxxxxxxxxxxxxxxxxxxxxxxxxx

  播放段落

  Similarly, to derive the Pythagorean identity  $\begin{array}{r}{\tan }^{2}x+1={\sec }^{2}x\end{array}$ , divide through by  $\begin{array}{r}{\cos }^{2}x\end{array}$  and simplify.
  ::类似地,取出 Pythagorean 身份 tan2x+1 =sec2x, 以 cos2x 和简化方式分隔 。

  播放段落

  $$\begin{array}{rl}\frac{{\sin }^{2}x}{{\cos }^{2}x}+\frac{{\cos }^{2}x}{{\cos }^{2}x}& =\frac{1}{{\cos }^{2}x}\\ {\tan }^{2}x+1& ={\sec }^{2}x\end{array}$$

  
  ::xcos2x+cos2xcos2xxcos2x=1cos2xtan2x+1=sec2xx

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if $\begin{array}{r}{\tan }^{2}x+{\cot }^{2}x=1\end{array}$  is a legitimate identity. Cofunctions are not always connected directly through a Pythagorean identity.
  ::早些时候, 您被问及是否 tan2 {x+cot2}x=1 是合法身份 。 函数并不总是通过 Pydagoren 身份直接连接 。

  播放段落

  $\begin{array}{r}{\tan }^{2}x+{\cot }^{2}x\ne 1\end{array}$
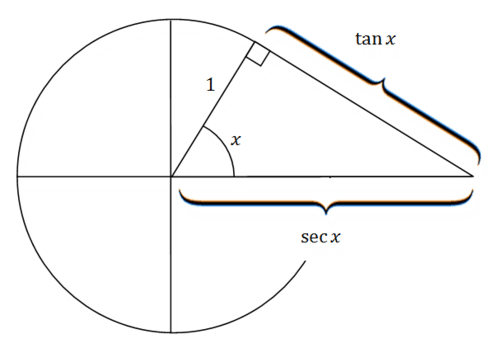
  ::tan2\\\ x+cot2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x+cot2\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Visually, the right triangle connecting tangent and secant can also be observed in the unit circle.  Most people do not know that tangent is named “tangent” because it refers to the distance of the line tangent from the point on the unit circle to the  $\begin{array}{r}x\end{array}$ axis.  Look at the picture below and think about why it makes sense that  $\begin{array}{r}\tan x\end{array}$ and $\begin{array}{r}\sec x\end{array}$  are as marked. $\begin{array}{r}\tan x=\frac{opp}{adj}\end{array}$ .  Since the adjacent side is equal to 1 (the radius of the circle), $\begin{array}{r}\tan x\end{array}$  simply equals the opposite side.  Similar logic can explain the placement of $\begin{array}{r}\sec x\end{array}$ .
  ::从视觉上看,连接正切和偏移的右三角也可以在单位圆中观察到。 大多数人不知道正切的名称是“ 切点 ” , 因为它指的是从单位圆的点到x轴的线切点之间的距离。 看看下面的图画, 想想为什么Tanx和cex的标记是有道理的。 tanx=oppadj。 由于相邻的一面等于1( 圆的半径) , tanx 仅仅等于相反的一面。 类似的逻辑可以解释 sex 的位置 。

  

  播放段落

  Example 2
  ::例2

  播放段落

  Simplify the following expression: $\begin{array}{r}\frac{\sin x(\csc x-\sin x)}{1-\sin x}\end{array}$ .
  ::简化以下表达式: sinx( cscx-sinx)1-sinx。

  播放段落

  $$\begin{array}{rl}\frac{\sin x(\csc x-\sin x)}{1-\sin x}& =\frac{\sin x\cdot \csc x-{\sin }^{2}x}{1-\sin x}\\ & =\frac{1-{\sin }^{2}x}{1-\sin x}\\ & =\frac{(1-\sin x)(1+\sin x)}{1-\sin x}\\ & =1+\sin x\end{array}$$

  
  :cscx-sinx)1-sinx=sinxxx-sin2x1-sinx=1-sin2x1-sinxxx=1-sin2x1-sinx(1+sinx)1-sinx=1+1+sinx)1-sinx=1+sin}xx=1x

  播放段落

  Note that factoring the Pythagorean identity is one of the most powerful and common applications. 
  ::请注意,保理毕达哥里人的身份是最有力和最常用的用途之一。

  播放段落

  Example 3
  ::例3

  播放段落

  Prove the following trigonometric identity : $\begin{array}{r}({\sec }^{2}x+{\csc }^{2}x)-({\tan }^{2}x+{\cot }^{2}x)=2\end{array}$
  ::证明下列三角测量特性sec2x+csc2x)-(tan2x+cot2x)=2

  播放段落

  Group the terms and apply a different form of the second two Pythagorean identities which are $\begin{array}{r}1+{\cot }^{2}x={\csc }^{2}x\end{array}$ and $\begin{array}{r}{\tan }^{2}x+1={\sec }^{2}x\end{array}$ .
  ::组合词组,并使用另一种形式的第二两种比达哥里安身份,即 1+cot2x=csc2x和tan2x+1=sec2x。

  播放段落

  $$\begin{array}{rl}({\sec }^{2}x+{\csc }^{2}x)-({\tan }^{2}x+{\cot }^{2}x)& ={\sec }^{2}x-{\tan }^{2}x+{\csc }^{2}x-{\cot }^{2}x\\ & =1+1\\ & =2\end{array}$$

  
  :sec2x+csc2x)-(tan2x+cot2x)=se2x-tan2x+csc2x-csc2x-cot2x=1+1=2)

  播放段落

  Example 4
  ::例4

  播放段落

  Simplify the following expression. Note:  $\begin{array}{r}{\sec }^{2}x=\frac{1}{{\cos }^{2}x}\end{array}$
  ::简化以下表达式 。 注意: sec2_ x=1cos2_ x

  播放段落

  $\begin{array}{r}({\sec }^{2}x)(1-{\sin }^{2}x)-\left(\frac{\sin x}{\csc x}+\frac{\cos x}{\sec x}\right)\end{array}$
  :sec2x)(1-sin2x) - (sinxcscx+cosxsecx)

  播放段落

  $$\begin{array}{rl}& ({\sec }^{2}x)(1-{\sin }^{2}x)-\left(\frac{\sin x}{\csc x}+\frac{\cos x}{\sec x}\right)\\ & ={\sec }^{2}x\cdot {\cos }^{2}x-({\sin }^{2}x+{\cos }^{2}x)\\ & =1-1\\ & =0\end{array}$$

  
  :sec2x) 1 - 辛2xxx) - (sinxcscx+cos*xsece*x) =sec2xxcos2xx- (sin2x+cos2x) =1-1=0

  播放段落

  Example 5
  ::例5

  播放段落

  Simplify the following expression.
  ::简化以下表达式 。

  播放段落

  $\begin{array}{r}(\cos t-\sin t{)}^2+(\cos t+\sin t{)}^2\end{array}$
  :cost-sint)2+(cost+sint)2

  播放段落

  Note that initially, the expression is not the same as the Pythagorean identity.
  ::请注意,最初的表达方式与毕达哥里人的身份不同。

  播放段落

  $$\begin{array}{rl}& (\cos t-\sin t{)}^2+(\cos t+\sin t{)}^2\\ & ={\cos }^{2}t-2\cos t\sin t+{\sin }^{2}t+{\cos }^{2}t+2\cos t\sin t+{\sin }^{2}t\\ & =1-2\cos t\sin t+1+2\cos t\sin t\\ & =2\end{array}$$

  
  :cost-sint) 2+(cost+sint) 2=cos2t-2coststsint+sin2t+cos2t+2cost}}t=1-2cost+1+2cosin}t=2

  Summary

  播放段落 The Pythagorean identity for sine and cosine is derived from a right triangle in a unit circle: $\begin{array}{r}{\sin }^{2}x+{\cos }^{2}x=1.\end{array}$   ::正弦和共弦的比达哥里安特性来自单位圆的右三角: sin2\\ x+cos2\\ x=1。 播放段落 Two other Pythagorean identities exist for trigonometric functions: $\begin{array}{r}1+{\tan }^{2}x={\sec }^{2}x\end{array}$  and $\begin{array}{r}1+co{t}^{2}x=cs{c}^{2}x.\end{array}$   ::三角函数中存在另外两个Pythagorean身份:1+tan2x=sec2x和1+cot2x=csc2x。

  播放段落

  Review
  ::回顾

  播放段落

  Prove each of the following:
  ::证明以下各点:

  播放段落

  1.  $\begin{array}{r}(1-{\cos }^{2}x)(1+{\cot }^{2}x)=1\end{array}$
  ::1. (1 - cos2x)(1+cot2x)=1

  播放段落

  2. $\begin{array}{r}\cos x(1-{\sin }^{2}x)={\cos }^{3}x\end{array}$
  ::2. COsx(1- 辛2x) =cos3x

  播放段落

  3.  $\begin{array}{r}{\sin }^{2}x=(1-\cos x)(1+\cos x)\end{array}$
  ::3 sin2 x = (1 - cosx (1+cosx))

  播放段落

  4.  $\begin{array}{r}\sin x=\frac{{\sin }^{2}x+{\cos }^{2}x}{\csc x}\end{array}$
  ::4. sin *x=sin2*x+cos2*xcsc*x

  播放段落

  5.  $\begin{array}{r}{\sin }^{4}x-{\cos }^{4}x={\sin }^{2}x-{\cos }^{2}x\end{array}$
  ::5 sin4x-cos4x=sin2x-cos2xxx

  播放段落

  6.  $\begin{array}{r}{\sin }^{2}x{\cos }^{3}x=({\sin }^{2}x-{\sin }^{4}x)(\cos x)\end{array}$
  ::6.2xcos3x=( 辛2x- 辛4x) (cosx)

  播放段落

  Simplify each expression as much as possible.
  ::尽可能简化每个表达式。

  播放段落

  7.  $\begin{array}{r}{\tan }^{3}x{\csc }^{3}x\end{array}$
  ::7.3xcsc3x

  播放段落

  8.  $\begin{array}{r}\frac{{\csc }^{2}x-1}{{\sec }^{2}x}\end{array}$
  ::8. csc2x-1sec2x

  播放段落

  9.  $\begin{array}{r}\frac{1-{\sin }^{2}x}{1+\sin x}\end{array}$
  ::9. 1 - 辛2x1+辛%x

  播放段落

  10.  $\begin{array}{r}\sqrt{1-{\cos }^{2}x}\end{array}$
  ::10. 1 - COs2 x

  播放段落

  11.  $\begin{array}{r}\frac{{\sin }^{2}x-{\sin }^{4}x}{{\cos }^{2}x}\end{array}$
  ::11.2x-sin4xxcos2xxxxxxxxxxxxxxxx

  播放段落

  12.  $\begin{array}{r}(1+{\tan }^{2}x)({\sec }^{2}x)\end{array}$
  ::12. (1+tan2x)(sec2x)

  播放段落

  13.  $\begin{array}{r}\frac{{\sin }^{2}x+{\tan }^{2}x+{\cos }^{2}x}{\sec x}\end{array}$
  ::13.2x+tan2x+cos2xxsecxxxxxxxxxxxxxx

  播放段落

  14.  $\begin{array}{r}\frac{1+{\tan }^{2}x}{{\csc }^{2}x}\end{array}$
  ::14. 1+tan2xcsc2x

  播放段落

  15.  $\begin{array}{r}\frac{1-{\sin }^{2}x}{\cos x}\end{array}$
  ::15. 1 - 辛2xcosxx

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。