课程： 6.5 三角等同 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

三角数等量

Solving a trigonometric equation is just like solving a regular equation. You will use factoring and other algebraic techniques to get the variable on one side. The biggest difference with trigonometric equations is the opportunity for there to be an infinite number of solutions that must be described with a pattern. The equation $\begin{aligned} \cos x = 1 \end{aligned}$ has many solutions including 0 and $\begin{aligned} 2 π \end{aligned}$ . How would you describe all of them?
::解析三角方程式就像解析正方程式一样。您将使用乘法和其他代数技术将变量放在一边。三角方程式的最大区别在于, 有机会找到无限数量的解决方案, 且必须用一个模式来描述。方程式=1 有许多解决方案, 包括 0 和 2 。您如何描述所有这些 ?

Solving Trigonometric Equations
::解决三角等量等量

The identities you have learned are helpful in solving trigonometric equations . The goal of solving an equation hasn’t changed. Do whatever it takes to get the variable alone on one side of the equation. Factoring, especially with the Pythagorean identity , is critical.
::您所学到的身份有助于解决三角方程式。解决方程式的目标没有改变。尽一切可能将变量单放在方程式的一边。保理(特别是Pythagoren身份的保理)至关重要。

Try to give exact (non-rounded) answers when solving trigonometric equations. If you are working with a calculator, keep in mind that while some newer calculators can provide exact answers like $\begin{aligned} \frac{\sqrt{3}}{2} \end{aligned}$ , most calculators will produce a decimal of 0.866... If you see a decimal like 0.866..., try squaring it. The result might be a nice fraction like $\begin{aligned} \frac{3}{4} \end{aligned}$ . Then you can logically conclude that the original decimal must be the square root of $\begin{aligned} \frac{3}{4} \end{aligned}$ or $\begin{aligned} \frac{\sqrt{3}}{2} \end{aligned}$ .
::在解析三角方程式时, 尝试给出精确( 非四舍五入) 答案。如果您正在使用计算器, 请记住, 虽然一些新计算器可以提供精确的答案, 例如 32 , 大多数计算器将产生小数点为 0. 866... 如果您看到小数点为 0. 866... , 请尝试对齐。结果可能会是34 这样的小数点。然后您可以逻辑地得出结论, 原始小数点必须是 34 或 32 的平方根。

When solving, if the two sides of the equation are always equal, then the equation is an identity. If the two sides of an equation are never equal, as with $\begin{aligned} \sin x = 3 \end{aligned}$ , then the equation has no solution.
::当解答时,如果方程式的两面总是对等的,那么方程式就是一个身份。如果方程式的两面从不相等,就像sinx=3一样,那么方程式就没有解决办法。

Examples
::实例

Example 1
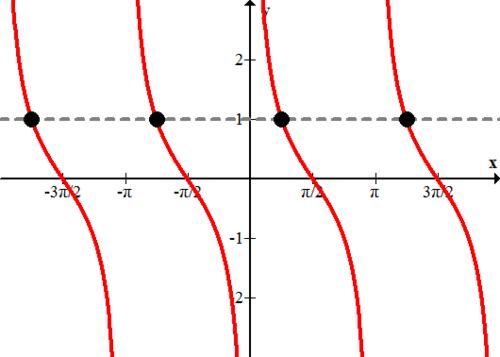
::例1

Earlier, you were asked how you could describe the many solutions of $\begin{aligned} \cos x = 1 \end{aligned}$ . When you type $\begin{aligned} \cos^{- 1} 1 \end{aligned}$ on your calculator, it will yield only one solution which is 0. In order to describe all the solutions you must use logic and the graph to figure out that cosine also has a height of 1 at $\begin{aligned} - 2 π, 2 π, - 4 π, 4 π \dots \end{aligned}$ Luckily all these values are sequences in a clear pattern so you can describe them all in general with the following notation:
::早些时候,有人问您如何描述 osx=1 的多种解决方案。当您在计算器上输入 os- 11 时, 它只产生一个为 0 的解决方案。为了描述所有您必须使用逻辑和图解的解决方案, 才能发现连弦的高度也高达 1 : - 2 2 2, - 4 4... 幸运的是, 所有这些值都是清晰的序列, 您可以用以下的符号来描述它们:

$\begin{aligned} x = 0 \pm n \cdot 2 π \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is an integer, or $\begin{aligned} x = \pm n \cdot 2 π \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is an integer.
::x=0n2n为整数,或 xn2nn为整数。

Example 2
::例2

Solve the following equation algebraically and confirm graphically on the interval $\begin{aligned} [- 2 π, 2 π] \end{aligned}$ .
::以代数方式解决以下方程式,并在间隔处用图形确认[-2,2]。

$\begin{aligned} \cos 2 x = \sin x \end{aligned}$
::COs%% 2x=sinx

$\begin{aligned} \cos 2 x & = \sin x \\ 1 - 2 \sin^{2} x & = \sin x \\ 0 & = 2 \sin^{2} x + \sin x - 1 \\ 0 & = (2 \sin x - 1) (\sin x + 1) \end{aligned}$

::COs2x=sinx1-2sin2}2x=sinx0=2sin2}x+sinx-10=(2sinx-1)(sinx+1)

Solving the first part set equal to zero within the interval yields:
::在间隔收益率范围内解决设定为零的第一部分 :

\begin{aligned} 0 & = 2 \sin x - 1 \\ \frac{1}{2} & = \sin x \\ x & = \frac{π}{6}, \frac{5 π}{6}, - \frac{11 π}{6}, - \frac{7 π}{6} \end{aligned}

::0=2sinx-112=sinxxxxxx6,56,6-116,-76

Solving the second part set equal to zero yields:
::解决第二部分设定的等于零产量:

\begin{aligned} 0 & = \sin x + 1 \\ - 1 & = \sin x \\ x & = - \frac{π}{2}, \frac{3 π}{2} \end{aligned}

::0=sinx+1-1=sinxxxxxxx2,32

These are the six solutions that will appear as intersections of the two graphs $\begin{aligned} f (x) = \cos 2 x \end{aligned}$ and $\begin{aligned} g (x) = \sin x \end{aligned}$ .
::这些是作为两个图f(x) = cos= 2x 和 g(x) = sinx 的交叉点出现的六个解决方案。

Example 3
::例3

Determine the general solution to the following equation.
::确定以下方程式的一般解决办法。

$\begin{aligned} \cot x - 1 = 0 \end{aligned}$
::comtx- 1=0

$\begin{aligned} \cot x - 1 & = 0 \\ \cot x & = 1 \end{aligned}$

::comtx- 1 = 0ctx= 1

One solution is $\begin{aligned} x = \frac{π}{4} \end{aligned}$ . However, since this question asks for the general solution, you need to find every possible solution. You have to know that cotangent has a period of $\begin{aligned} π \end{aligned}$ which means if you add or subtract $\begin{aligned} π \end{aligned}$ from $\begin{aligned} \frac{π}{4} \end{aligned}$ then it will also yield a height of 1. To capture all these other possible $\begin{aligned} x \end{aligned}$ values you should use this notation.
::一个是 x4 。但是, 既然这个问题需要通用解决方案, 您需要找到所有可能的解决方案。您必须知道, 余切有期。这意味着, 如果您从 4 中增加或减去 , 那么它也会产生 1 的高度。要捕捉所有这些其他可能的 x 值, 您应该使用此符号。

$\begin{aligned} x = \frac{π}{4} \pm n \cdot π \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is a integer
::n 是整数的 x4n

Notice that trigonometric equations may have an infinite number of solutions that repeat in a certain pattern because they are periodic functions. When you see these directions remember to find all the solutions by using notation like in this example.
::请注意三角方程式可能有无限数量的解决方案, 以某种模式重复, 因为它们是周期函数。当您看到这些方向时, 请记住要通过使用此示例中的标记来找到所有解决方案。

Example 4
::例4

Solve the following equation.
::解决以下方程式。

$\begin{aligned} 4 \cos^{2} x - 1 = 3 - 4 \sin^{2} x \end{aligned}$
::4cos2x- 1=3- 4sin2x

$\begin{aligned} 4 \cos^{2} x - 1 & = 3 - 4 \sin^{2} x \\ 4 \cos^{2} x + 4 \sin^{2} x & = 3 + 1 \\ 4 (\cos^{2} x + \sin^{2} x) & = 4 \\ 4 & = 4 \end{aligned}$

::4cos2%x- 1=3- 4sin2x4cos2x+4sin2x=3+14(cos2x+sin2x)=44=4

This equation is always true which means the right side is always equal to the left side. This is an identity.
::此等式总是对的, 这意味着右侧总是等于左侧。这是一个特性。

Example 5
::例5

Solve the following equation exactly.
::确切地解决以下方程。

$\begin{aligned} 2 \cos^{2} x + 3 \cos x - 2 = 0 \end{aligned}$
::2cos2x+3cosx-2=0

Start by factoring:
::以保理因素开始 :

\begin{aligned} 2 \cos^{2} x + 3 \cos x - 2 & = 0 \\ (2 \cos x - 1) (\cos x + 2) & = 0 \end{aligned}

::2cos2x+3cosx-2=0(2cos_x-1)(cos_x+2)=0

Note that $\begin{aligned} \cos x \neq - 2 \end{aligned}$ which means only one equation needs to be solved for solutions.
::注意Cosx2 意思是只要一个方程式就能解决问题。

\begin{aligned} 2 \cos x - 1 & = 0 \\ \cos x & = \frac{1}{2} \\ x & = \frac{π}{3}, - \frac{π}{3} \end{aligned}

::2cosx- 1= 0cosx= 12x3,%3

These are the solutions within the interval $\begin{aligned} - π \end{aligned}$ to $\begin{aligned} π \end{aligned}$ . Since this represents one full period of cosine, the rest of the solutions are just multiples of $\begin{aligned} 2 π \end{aligned}$ added and subtracted to these two values.
::这些是 \ \ 至 \ 的间隔内的解决办法。由于这代表一个完整的余弦期, 其余的解决方案只是这两个值中增加和减去的 2 ++ 的倍数。

$\begin{aligned} x = \pm \frac{π}{3} \pm n \cdot 2 π \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is an integer
::n是整数的 x3n2

Summary

Solving trigonometric equations involves using factoring and algebraic techniques to isolate the variable, just like solving regular equations.
::解决三角方程式需要使用乘数和代数技术来分离变量就像解决常规方程式一样

Some trigonometric equations can have an infinite number of solutions, which must be described with a pattern.
::一些三角方程式可以有无限数量的解决方案,必须用一个模式来描述。

When solving trigonometric equations, try to give exact (non-rounded) answers and use logic to deduce values from calculator results.
::在解决三角方程时,尝试给出准确(非四舍五入)的答案,并使用逻辑从计算结果中推算值。

If the two sides of an equation are always equal, it is an identity; if they are never equal, the equation has no solution.
::如果一个等式的两面永远是平等的,它就是一种特性;如果它们永远不是平等的,这个等式就没有解决办法。

Review
::回顾

Solve each equation on the interval $\begin{aligned} [0, 2 π) \end{aligned}$ .
::在间隔[0,2]中解决每个方程。

1. $\begin{aligned} 3 \cos^{2} \frac{x}{2} = 3 \end{aligned}$
::1. 3cos2x2=3

2. $\begin{aligned} 4 \sin^{2} x = 8 \sin^{2} \frac{x}{2} \end{aligned}$
::2. 4sin2x=8sin2x2

Find approximate solutions to each equation on the interval $\begin{aligned} [0, 2 π) \end{aligned}$ .
::在间距[0,2]为每个方程寻找近似解决办法。

3. $\begin{aligned} 3 \cos^{2} x + 10 \cos x + 2 = 0 \end{aligned}$
::3. 3cos2x+10cosx+2=0

4. $\begin{aligned} \sin^{2} x + 3 \sin x = 5 \end{aligned}$
::4 sin2 x+3sinx=5

5. $\begin{aligned} \tan^{2} x + \tan x = 3 \end{aligned}$
::5. tan2x+tanx=3

6. $\begin{aligned} \sin^{2} x + \cos^{2} x = 1 \end{aligned}$
::6.2x+cos2x=1

Solve each equation on the interval $\begin{aligned} [0, 360^{\circ}) \end{aligned}$ .
::在间隔[0,360]中解决每个方程。

7. $\begin{aligned} 2 \sin (x - \frac{π}{2}) = 1 \end{aligned}$
::7. 2sin(x2)=1

8. $\begin{aligned} 4 \cos (x - π) = 4 \end{aligned}$
::8. 4cos(x)=4

Solve each equation on the interval $\begin{aligned} [2 π, 4 π) \end{aligned}$ .
::在间距[2,4]上解决每个方程。

9. $\begin{aligned} \cos^{2} x + 2 \cos x + 1 = 0 \end{aligned}$
::9. CO2x+2cosx+1=0

10. $\begin{aligned} 3 \sin x = 2 \cos^{2} x \end{aligned}$
::10. 3sinx=2cos2x

11. $\begin{aligned} \tan x \sin^{2} x = \tan x \end{aligned}$
::11. 太阳2xxxxxxxxxxxx

12. $\begin{aligned} \sin^{2} x + 1 = 2 \sin x \end{aligned}$
::12.2x+1=2sin#x

13. $\begin{aligned} \sec^{2} x = 4 \end{aligned}$
::13. 秒2x=4

14. $\begin{aligned} \sin^{2} x - 4 = \cos^{2} x - \cos 2 x - 4 \end{aligned}$
::14.2x-4=cos2x-cos2x-cos%2x-4

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

三角数等量

Solving Trigonometric Equations ::解决三角等量等量

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)