Course: 9.3 圆环 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

圆环

A circle is the collection of points that are the same distance from a single point. What is the connection between the Pythagorean Theorem and a circle?

Graphing Circles
::图表圆

The single point that all the points on a circle are equidistant from is called the center of the circle. A circle does not have a focus or a directrix, instead it simply has a center. Circles can be recognized immediately from the general equation of a conic when the coefficients of $\begin{aligned} x^{2} \end{aligned}$ and $\begin{aligned} y^{2} \end{aligned}$ are the same sign and the same value. Circles are not functions because they do not pass the vertical line test. The distance from the center of a circle to the edge of the circle is called the radius of the circle. The distance from one end of the circle through the center to the other end of the circle is called the diameter . The diameter is equal to twice the radius.
::圆圈上所有点的位置都与圆的中间点相等。圆圈没有焦点或直方向,而只是有一个中心。当 x2 和 y2 的系数是相同的符号和值相同时,圆圈可以从二次曲线的方程式中立即识别。圆圈不是函数,因为它们没有通过垂直线测试。圆圈中心到圆圈边缘的距离被称为圆圈的半径。圆圈一端到圆圈另一端的距离被称为直径。直径等于半径的两倍。

The graphing form of a circle is:
::圆形的图示形式是:

$\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$
:x-h)2+(y-k)2=r2

The center of the circle is at $\begin{aligned} (h, k) \end{aligned}$ and the radius of the circle is $\begin{aligned} r \end{aligned}$ . Note that this looks remarkably like the Pythagorean Theorem.
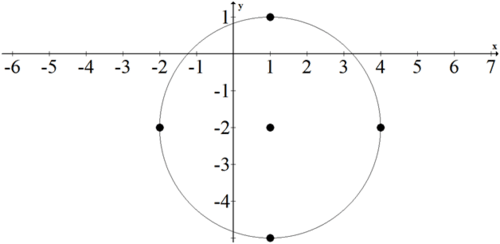
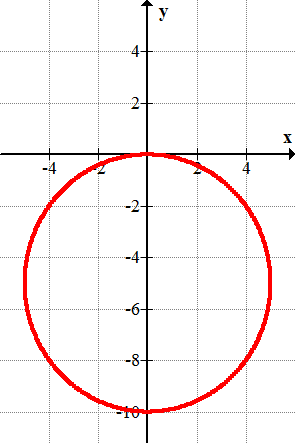
::圆的中心在 (h,k) ,圆的半径是 r。请注意, 这看上去非常像 Pytagorian Theorem 。

To graph a circle, first plot the center and then apply the radius. Take the following equation for a circle:
::要绘制圆形图,请先绘制中心,然后应用半径。对圆形采用以下方程式:

$\begin{aligned} (x - 1)^{2} + (y + 2)^{2} = 9 \end{aligned}$
:x-1)2+(y+2)2=9

The center is at $\begin{aligned} (1, - 2) \end{aligned}$ . Plot that point and the four points that are exactly 3 units from the center.
::中心在1,2-2处绘制点和4点正好是3个单位从中心。

Examples
::实例

Example 1
::例1

Earlier, you were asked about the connection between circles and the Pythagorean Theorem. The reason why the graphing form of a circle looks like the Pythagorean Theorem is because each $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ coordinate along the outside of the circle forms a perfect right triangle with the radius as the hypotenuse.
::早些时候,有人询问了圆圈和毕达哥里安理论之间的连接。为什么圆形的图形形式看起来像毕达哥里安理论,原因是每个x和y在圆圈的外部坐标形成一个完美的右三角形,以半径为下限。

Example 2
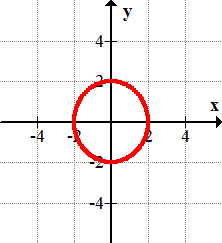
::例2

Graph the following conic: $\begin{aligned} (x + 2)^{2} + (y - 1)^{2} = 1 \end{aligned}$
::图如下二次曲线x+2)2+(y- 1)2=1

Example 3
::例3

Turn the following equation into graphing form for a circle. Identify the center and the radius.
::将以下方程式转换为圆形的图形化形式。识别中心与半径。

$\begin{aligned} 36 x^{2} + 36 y^{2} - 24 x + 36 y - 275 = 0 \end{aligned}$
::36x2+36y2-24x+36-275=0

Complete the square and then divide by the coefficient of $\begin{aligned} x^{2} \end{aligned}$ and $\begin{aligned} y^{2} \end{aligned}$
::完成方形,然后除以 x2 和 y2 的系数

\begin{aligned} 36 x^{2} - 24 x + 36 y^{2} + 36 y = 275 \\ 36 (x^{2} - \frac{2}{3} x + \underline{}) + 36 (y^{2} + y + \underline{}) = 275 \\ 36 (x^{2} - \frac{2}{3} x + \frac{1}{9}) + 36 (y^{2} + y + \frac{1}{4}) = 275 + 4 + 9 \\ 36 {(x - \frac{1}{3})}^{2} + 36 {(y + \frac{1}{2})}^{2} = 288 \\ {(x - \frac{1}{3})}^{2} + {(y + \frac{1}{2})}^{2} = 8 \end{aligned}

::36x2- 24x+3624x+36y2+36y=27536(x2- 23x)+36(y2+y)=27536(x2- 23x+19)+36(y2+y+y+14)=275+4+936(x- 13)2+36(y+12)2=288(x- 13)2+(y+12)2=8

The center is $\begin{aligned} (\frac{1}{3}, - \frac{1}{2}) \end{aligned}$ . The radius is $\begin{aligned} \sqrt{8} = 2 \sqrt{2} \end{aligned}$ .
::中心是(13,-12),半径是8=22。

Example 4
::例4

Write the equation for the following circle.
::写下圆的方程。

$\begin{aligned} (x - 1)^{2} + (y + 2)^{2} = 4 \end{aligned}$
:x-1)2+(y+2)2=4

Example 5
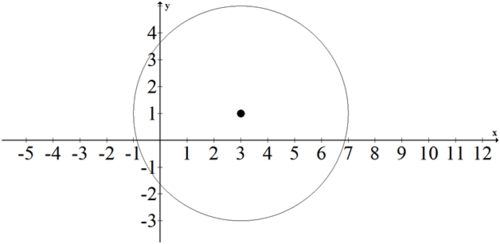
::例5

Write the equation of the following circle.
::写下圆的方程。

The center of the circle is at (3, 1) and the radius of the circle is $\begin{aligned} r = 4 \end{aligned}$ . The equation is $\begin{aligned} (x - 3)^{2} + (y - 1)^{2} = 16 \end{aligned}$ .
::圆的中心是(3, 1),圆的半径是(x-3)2+(y-1)2=16。

Summary

A circle is a collection of points that are equidistant from a single point, called the center.
::一个圆是一个集合点的集合点,从一个点,称为中点,其距离相等。

The distance from the center to the edge of the circle is called the radius, and the distance across the circle through the center is called the diameter, which is equal to twice the radius.
::从中间到圆边边缘的距离称为半径,圆中间的距离称为直径,等于半径的两倍。

Circles are not functions because they do not pass the vertical line test.
::圆圈不是函数,因为它们没有通过垂直线条测试。

The graphing form of a circle is $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2}, \end{aligned}$ where the center is at $\begin{aligned} (h, k) \end{aligned}$ and the radius is $\begin{aligned} r . \end{aligned}$
::圆形的图形形式是(x-h)2+(y-k)2=r2,中心位于(h,k),半径为r。

Review
::回顾

Graph the following conics:
::图形如下二次曲线:

1. $\begin{aligned} (x + 4)^{2} + (y - 3)^{2} = 1 \end{aligned}$
::1. (x+4)2+(y-3)2=1

2. $\begin{aligned} (x - 7)^{2} + (y + 1)^{2} = 4 \end{aligned}$
::2. (x-7)2+(y+1)2=4

3. $\begin{aligned} (y + 2)^{2} + (x - 1)^{2} = 9 \end{aligned}$
::3. (y+2)2+(x-1)2=9

4. $\begin{aligned} x^{2} + (y - 5)^{2} = 8 \end{aligned}$
::4. x2+(y-5-5)2=8

5. $\begin{aligned} (x - 2)^{2} + y^{2} = 16 \end{aligned}$
::5. (x-2)2+y2=16

Translate the following conics from standard form to graphing form.
::将以下二次曲线从标准窗体转换为图形化窗体。

6. $\begin{aligned} x^{2} - 4 x + y^{2} + 10 y + 18 = 0 \end{aligned}$
::6. x2-4x+y2+10y+18=0

7. $\begin{aligned} x^{2} + 2 x + y^{2} - 8 y + 1 = 0 \end{aligned}$
::7. x2+2x+y2-8y+1=0

8. $\begin{aligned} x^{2} - 6 x + y^{2} - 4 y + 12 = 0 \end{aligned}$
::8. x2-6x+y2-4y+12=0

9. $\begin{aligned} x^{2} + 2 x + y^{2} + 14 y + 25 = 0 \end{aligned}$
::9. x2+2x+y2+14y+25=0

10. $\begin{aligned} x^{2} - 2 x + y^{2} - 2 y = 0 \end{aligned}$
::10. x2-2x+y2-2y=0

Write the equations for the following circles.
::写下下列圆圈的方程。

11.

12.

13.

14.

15.

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

圆环

Graphing Circles ::图表圆

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)