Course: 2.2 单方面限制 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

片面限制

Tuscany and Sophia were out hiking. As they followed the path up the side of a hill, they discovered that there had been a washout from the recent storm. The path had been obliterated for a space of about 15 feet in front of them, but about 10 feet higher up it continued on up the mountain.
::托斯卡尼和索菲亚正在远足。当他们沿着山上的道路走过时,他们发现最近暴风雨已经冲洗了。这条道路被抹去,在他们前面大约15英尺的地方,但高大约10英尺,一直沿着山上。

How could this situation be explained with ?
::如何解释这种情况?

One-Sided Limits
::单设界限

We continue with the exploration of one-sided limits. Recall the definitions that we are using:
::我们继续探索单方面的限制。

A limit that is evaluated as $\begin{aligned} x \end{aligned}$ approaches the value $\begin{aligned} x = a \end{aligned}$ from one side only, left or right, is called a one-sided limit , and is represented by the following notation:
::当 x 仅从左侧或右侧接近 x=a 值时被评价的限值,称为单向限制,以下列符号表示:

\begin{aligned} Left sided : & lim_{x \to a^{-}} f (x) = L^{-} \\ Right sided : & lim_{x \to a^{+}} f (x) = L^{+} \end{aligned}

::左侧:limxa-f(x)=L-右侧:limxa+f(x)=L+

When both the left and right one-sided limits are evaluated as $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} a \end{aligned}$ , and $\begin{aligned} L^{-} = L^{+} = L \end{aligned}$ , only then do we write $\begin{aligned} lim_{x \to a} f (x) = L \end{aligned}$ . This limit $\begin{aligned} lim_{x \to a} f (x) = L \end{aligned}$ is called the two-sided limit . If $\begin{aligned} L^{-} \neq L^{+} \end{aligned}$ , we say the $\begin{aligned} lim_{x \to a} f (x) \end{aligned}$ does not exist .
::当左和右的单面限制被评价为 x 接近 a 和 LL 和 LL 时, 只有这样我们才会写入 limxaf(x) = L。这个限制 limxaf(x) = L 被称为双面限制。如果 LL+, 我们就会说 limxaf(x) 不存在。

The functions we explore in this concept may have the same or different limits for each “side” of the $\begin{aligned} x \end{aligned}$ value being evaluated. To evaluate these functions, we deal with each “side” separately: first evaluating what happens as $\begin{aligned} x \end{aligned}$ approaches from the left (the values of $\begin{aligned} x \end{aligned}$ are increasing); then evaluating what happens as $\begin{aligned} x \end{aligned}$ approaches from the right (the values of $\begin{aligned} x \end{aligned}$ are decreasing). When the value of $\begin{aligned} f (x) \end{aligned}$ does not get closer and closer to some single value $\begin{aligned} L \end{aligned}$ as $\begin{aligned} x \to x_{0} \end{aligned}$ we say that the limit of the function as $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} x_{0} \end{aligned}$ does not exist. We may separately state the limits for each “side” of $\begin{aligned} x_{0} \end{aligned}$ , but the complete function will only have a specified limit if it is the same for both sides.
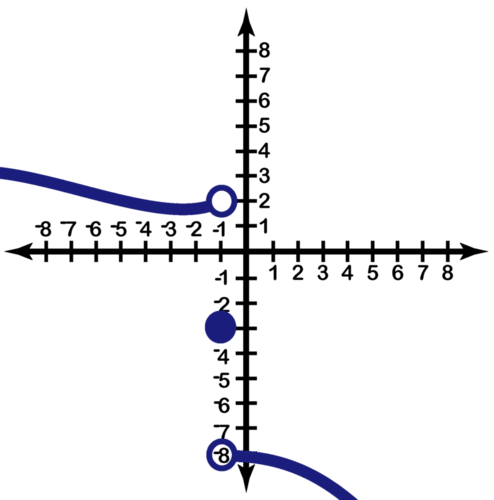
::我们在此概念中探索的函数可能对所评估的 x 值的每个“ 侧” 都有相同或不同的限制。为了评估这些函数, 我们分别处理每个“ 侧 ” : 首先评估左侧 x 向上走的情况( x 的值正在增加); 然后评估右侧 x 向上走的情况( x 的值正在减少 ) 。当 f( x) 的值没有接近或接近某些单一值L as xxxx0 时, 我们就会说, 作为 x 向上xx0 的函数的极限并不存在。我们可以分别说明 x0 的每个“ 侧” 的界限, 但完整函数只有对两侧都一样时, 才会有特定的限制。

Consider the function $\begin{aligned} f (x) \end{aligned}$ graphed in the accompanying figure and let's find:
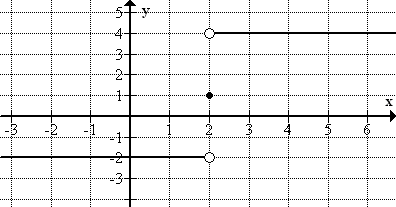
::考虑所附图中图表显示的函数 f( x) ,让我们找到 :

$\begin{aligned} lim_{x \to 2^{-}} f (x) \end{aligned}$
::limx%2 - f(x)

$\begin{aligned} lim_{x \to 2^{+}} f (x) \end{aligned}$
::limx%2+f(x)

$\begin{aligned} lim_{x \to 2} f (x) \end{aligned}$
::limx%2f(x)

$\begin{aligned} f (2) \end{aligned}$
::f(2) f(2)

From the graph, we can see that, $\begin{aligned} lim_{x \to 2^{-}} f (x) = - 2 \end{aligned}$ .
::从图中,我们可以看到, limx2-f(x)2。

We can also see from the graph that $\begin{aligned} lim_{x \to 2^{+}} f (x) = 4 \end{aligned}$ .
::我们也可以从Limx%2+f(x)=4的图中看到。

Since the limits from the right and the left are not equal (they do not approach a single value $\begin{aligned} L \end{aligned}$ ), the limit does not exist. That is $\begin{aligned} lim_{x \to 2} f (x) \end{aligned}$ does not exist.
::由于右和左的限值不相等(它们不接近单一值L),因此这一限值不存在。即 limx%2f(x) 不存在。

From the graph, $\begin{aligned} f (2) = 1 \end{aligned}$ .
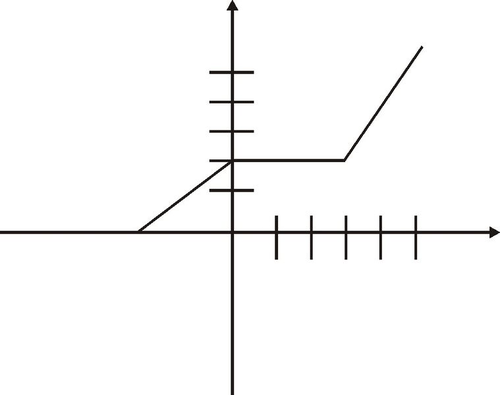
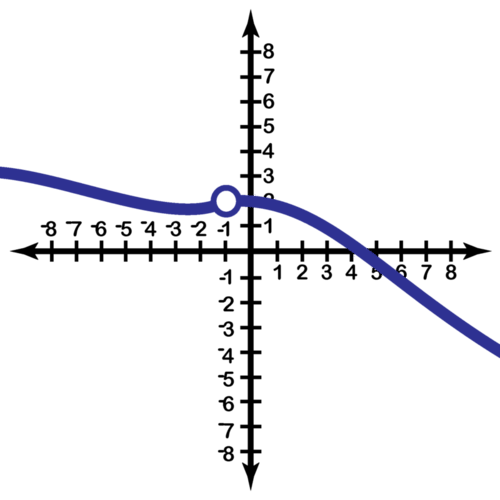
::图表中的 f(2)=1。

Now, consider the function pictured below and assume units of value 1 for each unit on the axes. Find $\begin{aligned} lim_{x \to 3} f (x) \end{aligned}$ .
::现在考虑下面的函数, 并假设轴上每个单位的值为 1。查找 limx}3f( x) 。

By inspection, we see that as we approach the value $\begin{aligned} x = 3 \end{aligned}$ from the left, we do so along what appears to be a portion of the horizontal line $\begin{aligned} y = 2 \end{aligned}$ , so the left-sided limit is given as: $\begin{aligned} lim_{x \to 3^{-}} f (x) = 2 \end{aligned}$ .
::通过检查,我们看到,当我们从左侧接近值x=3时,我们按照似乎属于水平线y=2的一部分的Y=2来这样做,所以左侧的极限是:limx3-f(x)=2。

We see that as we approach the value $\begin{aligned} x = 3 \end{aligned}$ from the right, we do so along a line segment having positive slope, and the left-sided limit can be written as: $\begin{aligned} lim_{x \to 3^{+}} f (x) = 2 \end{aligned}$ .
::我们看到,当我们从右边接近值x=3时,我们沿着具有正斜度的线段进行,左侧限制可以写成:limx3+f(x)=2。

Because both one-sided limits have the same value of 2, we can say: $\begin{aligned} lim_{x \to 3} f (x) = 2 \end{aligned}$ .
::因为两个片面限制的值都与2相同, 我们可以说: lix}3f(x)=2。

Examples
::实例

Example 1
::例1

Earlier, you were asked about Tuscany and Sophie's hiking path. The path had been washed out for about 15 feet in front of them, but continued about 10 feet higher on the mountain.
::早些时候,有人问你托斯卡尼和苏菲的徒步路线。这条道路在他们前面被冲了大约15英尺,但在山上继续走10英尺高。

Tuscany and Sophia's path could be examined as a discontinuous function of elevation based on distance traveled along the path. For instance, if Tuscany and Sophia had traveled for 500 yards along the path before encountering the washout, then the limit of the function from the “trailhead side” would be the elevation at the edge they encountered. The function would then be undefined for the next 5 yards or so (since the path does not exist), and would pick up at 506 yards, where the elevation would be 10 ft higher. If Sayber were coming down the path toward Tuscany and Sophia, from his point of view the “limit” of the elevation would be 10 ft greater, and would be the lowest elevation that “his side” of the function could attain.
::托斯卡尼和索菲亚的路径可以作为一个不连续的高度函数来检查。其依据是沿路行走的距离。比如,如果托斯卡尼和索菲亚在冲洗前沿路行走500码,那么“ 铁头边” 的功能极限就是他们遇到的边缘的高度。其功能随后将无法为下5码左右的高度( 因为这条路径不存在 ) , 并且会回到506码, 高度将高达10英尺。如果赛伯从他的角度走下通往托斯卡尼和索菲亚的道路, 高的“ 界限” 将更大10英尺, 并且是“ 他一边” 功能可以达到的最低高度。

Example 2
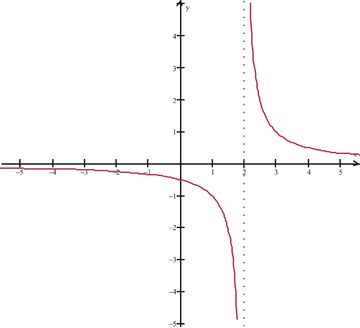
::例2

Find the limit $\begin{aligned} lim_{x \to 2} \frac{x + 3}{x^{2} + x - 6} \end{aligned}$ .
::查找限制的limx%2x+3x2+x-6。

The graph of $\begin{aligned} f (x) \end{aligned}$ is shown below.
::f(x) 图表如下。

Inspection of the graph shows that around $\begin{aligned} x = 2 \end{aligned}$ the function does not approach a particular value.
::对图形的检查显示,在 x=2 左右,函数没有接近特定值。

As $\begin{aligned} x \end{aligned}$ approaches 2 from the left (i.e. for $\begin{aligned} x < 2 \end{aligned}$ ), the values of $\begin{aligned} f (x) \end{aligned}$ near $\begin{aligned} x = 2 \end{aligned}$ all lie in the fourth quadrant and decrease to large negative numbers: $\begin{aligned} lim_{x \to 2^{-}} \frac{x + 3}{x^{2} + x - 6} = - \infty \end{aligned}$
::作为左侧的 x 向上方向 2 (即x < 2) , x=2 附近的 f(x) 值全部在第四象限内,减为大负数: limx% 2 - x+3x2+x-6

As $\begin{aligned} x \end{aligned}$ approaches 2 from the right (i.e., for $\begin{aligned} x > 2 \end{aligned}$ ), the values of $\begin{aligned} f (x) \end{aligned}$ near $\begin{aligned} x = 2 \end{aligned}$ all lie in the first quadrant and grow very quickly to large positive numbers: $\begin{aligned} lim_{x \to 2^{+}} \frac{x + 3}{x^{2} + x - 6} = \infty \end{aligned}$
::右侧的x 向上移2(即x>2),x=2附近的f(x)值全部位于第一个象限内,并迅速增长到较大正数: limx%2+x+3x2+x-6**========xxxxxxxxxxxxxxxxxxxxxxxx2+x-6================================================================================================================================================================================================================================================================================================================================================================================================================================

If we numerically calculate values of $\begin{aligned} f (x) \end{aligned}$ on either side of and very close to $\begin{aligned} x = 2 \end{aligned}$ , as shown in the table below, we can see that the one-sided limits are different.
::如果我们用数字计算下表所示的f(x)和非常接近x=2的f(x)两侧的数值,我们可以看到单向限制是不同的。

$\begin{aligned} x \end{aligned}$ ::x x	1.999	1.9999	2.0000	2.001	2.0001
$\begin{aligned} f (x) \end{aligned}$ :fx)	-1000	-10000	ERROR ::错误	10000	1000

We can write: $\begin{aligned} lim_{x \to 2^{-}} \frac{x + 3}{x^{2} + x - 6} = - \infty \end{aligned}$ and $\begin{aligned} lim_{x \to 2^{+}} \frac{x + 3}{x^{2} + x - 6} = \infty \end{aligned}$ .
::我们可以写下: limx%2 - x+3x2+x-6 和 limx%2+x+3x2+x-6。

For this example, we say that $\begin{aligned} lim_{x \to 2} \frac{x + 3}{x^{2} + x - 6} \end{aligned}$ does not exist.
::例如,我们说不存在limx%2x+3x2+x-6。

Example 3
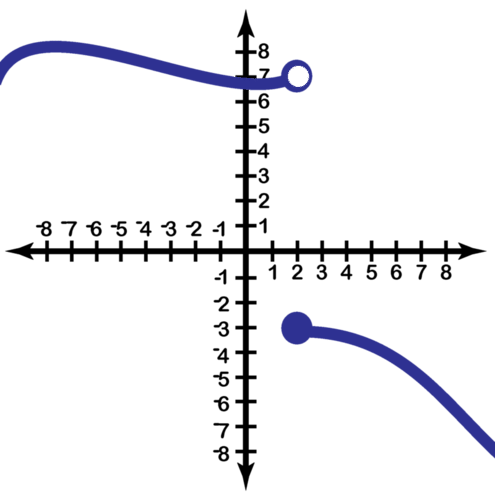
::例3

For the function $\begin{aligned} f (x) = \frac{6 x (x - 2)}{x - 1} \end{aligned}$ , graphed below, find the left and right sided limits at the value and the value $\begin{aligned} x = 3 \end{aligned}$
::函数 f( x) = 6x( x- 2) x- 1 时, 请在以下图表中找到值和值 x=3 的左侧和右侧限制值

Then, make a statement about the existence of the two-sided limit for each of the $\begin{aligned} x \end{aligned}$ values.
::然后,就每个 x 值存在双向限制作出说明。

Looking at $\begin{aligned} x = 1 \end{aligned}$ , inspection of the graph indicates that: $\begin{aligned} lim_{x \to 1^{-}} \frac{6 x (x - 2)}{x - 1} = \infty \end{aligned}$ and $\begin{aligned} lim_{x \to 1^{+}} \frac{6 x (x - 2)}{x - 1} = - \infty \end{aligned}$ .
::查看x=1, 图表显示: limx_1- 6x(x-2)x-1 和 limx_ 1+6x(x-2)x- 1。

This is supported by the table values below.
::以下表格数值支持这一点。

$\begin{aligned} x \end{aligned}$ ::x x	0.999	0.9999	1.0000	1.0001	1.001
$\begin{aligned} f (x) \end{aligned}$ :fx)	6000	60000	ERROR ::错误	-60000	-6000

We see that the one-sided limits are not the same, and therefore the limit (two-sided) of $\begin{aligned} f (x) \end{aligned}$ does not exist.
::我们认为,单方面的界限不同,因此f(x)的界限(两面)并不存在。

Looking at $\begin{aligned} x = 3 \end{aligned}$ , inspection of the graph indicates that: $\begin{aligned} lim_{x \to 3^{-}} \frac{6 x (x - 2)}{x - 1} = 9 \end{aligned}$ and $\begin{aligned} lim_{x \to 3^{+}} \frac{6 x (x - 2)}{x - 1} = 9 \end{aligned}$ .
::查看x=3, 图表显示: limx3-3-6x(x-2)x-1=9和limx3+6x(x-2)x-1=9。

This is supported by the table values below.
::以下表格数值支持这一点。

$\begin{aligned} x \end{aligned}$ ::x x	2.999	2.9999	3.0000	3.0001	3.001
$\begin{aligned} f (x) \end{aligned}$ :fx)	8.992	8.9992	9.0000	9.0007	9.007

We see that the one-sided limits are approaching the same value of 9, and therefore the limit (two-sided) of $\begin{aligned} f (x) \end{aligned}$ does exist. We can write: $\begin{aligned} lim_{x \to 3} \frac{6 x (x - 2)}{x - 1} = 9 \end{aligned}$ .
::我们看到,单方限制值接近9, 因此f(x) 的限值( 双面) 确实存在。我们可以写: limx36x( x-2)x- 1=9 。

Review
::回顾

For #1-5, identify the limit based on each graph.
::对于 # 1-5, 确定以每个图表为基础的限值。

$\begin{aligned} lim_{x \to - 3^{-}} \end{aligned}$

::3 - 3 - 3 -

$\begin{aligned} lim_{x \to 2^{+}} \end{aligned}$

::limx%2+

$\begin{aligned} lim_{x \to - 1^{+}} \end{aligned}$ and $\begin{aligned} lim_{x \to - 1^{-}} \end{aligned}$

::limx1+ 和limx1-

$\begin{aligned} lim_{x \to - 1} \end{aligned}$

::立方公尺1

$\begin{aligned} lim_{x \to - 2^{-}} \end{aligned}$ and $\begin{aligned} lim_{x \to 5^{+}} \end{aligned}$

::limx%2 - 和limx=5+

For #6-18, identify the limit based on the equation.
::对于#6-18,根据方程指定限制。

$\begin{aligned} lim_{x \to 2^{+}} \frac{- x^{2} - 2 x + 8}{x - 2} = \end{aligned}$
::立方公尺xx2x2 - 2x+8x-2=

$\begin{aligned} lim_{x \to - 3} g (x) = {\begin{cases} 4; x = - 3 \\ 1; x \neq - 3 \end{cases} \end{aligned}$
::立方公尺x%3g( x) 4; x31; x3

$\begin{aligned} lim_{x \to 0^{+}} \frac{- x^{2} + 4 x}{x} = \end{aligned}$
::立方公尺xxx2+4xx=

$\begin{aligned} lim_{x \to - 1} g (x) = {\begin{cases} - 5; x \neq - 1 \\ - 1; x = - 1 \end{cases} \end{aligned}$
::limx1g( x)%5; x1 -1; x1

$\begin{aligned} lim_{x \to 1^{+}} \frac{4 x^{2} - x - 3}{x - 1} = \end{aligned}$
::limx%1+4x2-x-3x-1=

$\begin{aligned} lim_{x \to 3} f (x) = {\begin{cases} 4; x \geq 3 \\ x + 1; x < 3 \end{cases} \end{aligned}$
::limx%3f( x) @%4; x%3x+1; x<3

$\begin{aligned} lim_{x \to 0^{+}} \frac{x^{2} - 4 x}{x} = \end{aligned}$
::limx=0+x2-4xx=

$\begin{aligned} lim_{x \to 2} h (x) = {\begin{cases} 4 x + 4; x \neq 2 \\ 1; x = 2 \end{cases} \end{aligned}$
::limx2h( x) 4x+4; x21; x=2

$\begin{aligned} lim_{x \to 2^{-}} \frac{4 x^{2} - 7 x - 2}{x - 2} = \end{aligned}$
::2 - 4x2 - 7x - 2x-2=

$\begin{aligned} lim_{x \to - 2} g (x) = {\begin{cases} x - 5; x = - 2 \\ 4 x + 1; x \neq - 2 \end{cases} \end{aligned}$
::limbx% 2g( x) x- 5; x24x+1; x2

$\begin{aligned} g (x) = {\begin{cases} - 3; x \neq 3 \\ - 9; x = 3 \end{cases} \end{aligned}$
::g( x)\\\\\ 3; x\\\\ 9; x=3

$\begin{aligned} lim_{x \to - 5^{-}} \frac{- 3 x^{2} - 13 x + 10}{x + 5} = \end{aligned}$
::立方公尺xx5x3x2-13x+10x+5=

$\begin{aligned} f (x) = {\begin{cases} x; x = 2 \\ 3 x - 3; x \neq 2 \end{cases} \end{aligned}$
:xx) x; x=23x- 3; x2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

片面限制

One-Sided Limits ::单设界限

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)