Course: 2.4 涉及无限的限制

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 涉及无限的限制

Collapse Expand
涉及无限的限制
Some functions increase without bound (get larger and larger) as the absolute value of the independent variable gets larger and larger. Some functions increase without bound as the independent variable goes toward a specific value. Can you think of an example of a function that exhibits behavior in each category?
::有些函数随着独立变量的绝对值越来越大而增加( 越大越大 ) 。有些函数随着独立变量转向特定值而增加。你能想象一个显示每个类别中行为的函数示例吗 ?

Limits Involving Infinity
::涉及无限的限制

The concept of “limits involving infinity” must be discussed in two contexts.
::“涉及无限的限制”的概念必须在两种情况下讨论。

First, we can discuss the value(s) a function attains as we increase $\begin{aligned} x \end{aligned}$ without bound. In this case we speak of the limit of $\begin{aligned} f (x) \end{aligned}$ as $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} \infty \end{aligned}$ , and write $\begin{aligned} lim_{x \to \infty} f (x) \end{aligned}$ . We could similarly refer to the limit of $\begin{aligned} f (x) \end{aligned}$ as $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} - \infty \end{aligned}$ and write $\begin{aligned} lim_{x \to - \infty} f (x) \end{aligned}$ . In this context, we are discussing the end behavior of the function. The function may attain a specific end value, e.g. 0, or increase without bound.
::首先,我们可以讨论一个函数随着我们增加x而实现的值。在此情况下, 我们谈论 f( x) 的限度是 x 的接近 {} {} , 并写入 limx {} f( x) 。我们也可以同样地提及 f( x) 的限度是 x 的接近 {} {} , 并写入 limx {} f( x) 。在此情况下, 我们正在讨论该函数的最终行为。该函数可能达到特定的结束值, 如 0, 或不加约束而增加。

Secondly, we can discuss the situation where the values of a function increase without bound as the value of $\begin{aligned} x \end{aligned}$ approaches a specific value. In this case, we speak of the limit of $\begin{aligned} f (x) \end{aligned}$ approaching $\begin{aligned} \infty \end{aligned}$ or $\begin{aligned} - \infty \end{aligned}$ as $\begin{aligned} x \end{aligned}$ approaches the specific value, e.g., $\begin{aligned} lim_{x \to a} f (x) = \infty \end{aligned}$ .
::其次,我们可以讨论一个函数的值在不受约束的情况下增加而x的值接近特定值的情况。在这种情况下,我们谈的是f(x)接近 {{} 或{}的限度,因为x接近具体值,例如 limxaf(x)}}}。

Consider the function $\begin{aligned} f (x) = x^{2} + 2 x - 3 \end{aligned}$ . What is $\begin{aligned} lim_{x \to \infty} f (x) \end{aligned}$ , i.e., the end behavior of $\begin{aligned} f (x) \end{aligned}$ ?
::考虑函数 f( x) =x2+2x-3。什么是 limxf( x) , 即 f( x) 的结束行为 ?

This question relates to the first context of limits involving infinity. As $\begin{aligned} x \end{aligned}$ goes to $\begin{aligned} \infty \end{aligned}$ or $\begin{aligned} - \infty \end{aligned}$ , $\begin{aligned} f (x) \end{aligned}$ increases without bound and $\begin{aligned} f (x) \approx x^{2} \end{aligned}$ , since the $\begin{aligned} x^{2} \end{aligned}$ value grows much more quickly than the $\begin{aligned} 2 x \end{aligned}$ value. If this is not immediately apparent, evaluate the function for $\begin{aligned} x = 1, 000, 000 \end{aligned}$ , and you will quickly get the idea! The curve $\begin{aligned} f (x) \approx x^{2} \end{aligned}$ is considered an asymptote of $\begin{aligned} f (x) \end{aligned}$ , i.e., the curve that $\begin{aligned} f (x) \end{aligned}$ tends to at large absolute values of $\begin{aligned} x \end{aligned}$ .
::这个问题涉及到涉及无限度的限制的第一个上下文。由于 x 到或 , f(x) 增加无约束值和 f(x) x2, 因为 x2 值的增长速度比 2x 值要快得多。如果这不立即明显, 请评估 x= 100万的函数, 您很快就会得到这个想法 ! 曲线 f(x) x2 被视为 f(x) 的零星值, 即 f(x) 倾向于很大绝对值 x 的曲线。

Therefore both $\begin{aligned} lim_{x \to \infty} f (x) = \infty \end{aligned}$ and $\begin{aligned} lim_{x \to - \infty} f (x) = \infty \end{aligned}$ , and we can use the function $\begin{aligned} y = x^{2} \end{aligned}$ to describe the end behavior of $\begin{aligned} f (x) \end{aligned}$ .
::因此, limxf(x) 和 limxf(x), 我们可以使用 y=x2 来描述 f(x) 的结束行为。

Examples
::实例

Example 1
::例1

Earlier, you were asked to think of an example of a function that grows without bound as $\begin{aligned} x \end{aligned}$ goes to positive or negative infinity and an example of a function that grows without bound at a specific value of $\begin{aligned} x \end{aligned}$ . There are many possible examples of rational functions that will do. Just consider a case where the degree of the numerator is greater than the denominator, and the denominator goes to 0 for a specific value of $\begin{aligned} x \end{aligned}$ .
::早些时候,有人要求您想象一个无约束地成长的函数的例子,因为x会变成正的或负的无限性,另一个无约束地成长的函数的例子,没有特定值的x。有很多可能的理性函数的例子可以做到。只要考虑一个数字的大小大于分母,而分母对于特定值是x,则分母会增加到0。

For example: $\begin{aligned} f (x) = \frac{x^{4}}{x - 2} \end{aligned}$ , has asymptotic end behavior $\begin{aligned} f (x) \approx x^{3} \end{aligned}$ , and vertical asymptote at $\begin{aligned} x = 2 \end{aligned}$ .
::例如: f( x) =x4x-2, 具有无ymptatic 结束行为 f( x)\\\\\\\ x3, 和 x=2 时的垂直无ymptote 。

Example 2
::例2

Find $\begin{aligned} lim_{x \to \infty} \frac{2 x^{3} - x^{2} + x - 1}{x^{6} - x^{5} + 3 x^{4} - 2 x + 1} \end{aligned}$ .
::查找 limx%2x3 - x2+x- 1x6 - x5+3x4 - 2x+1 。

Note that we cannot immediately apply the Quotient Property because we have the indeterminate form $\begin{aligned} \frac{\infty}{\infty} \end{aligned}$ . However, if we first divide both numerator and denominator by the quantity $\begin{aligned} x^{6} \end{aligned}$ , we will then have a function of the form
::请注意,我们无法立即应用数字属性,因为我们有不确定的表格 {{{}}{}。然而,如果我们首先将分子和分母除以数量x6,那么我们将具有该格式的函数。

$\begin{aligned} \frac{f (x)}{g (x)} = \frac{\frac{2 x^{3}}{x^{6}} - \frac{x^{2}}{x^{6}} + \frac{x}{x^{6}} - \frac{1}{x^{6}}}{\frac{x^{6}}{x^{6}} - \frac{x^{5}}{x^{6}} + \frac{3 x^{4}}{x^{6}} - \frac{2 x}{x^{6}} + \frac{1}{x^{6}}} = \frac{\frac{2}{x^{3}} - \frac{1}{x^{4}} + \frac{1}{x^{5}} - \frac{1}{x^{6}}}{1 - \frac{1}{x} + \frac{3}{x^{2}} - \frac{2}{x^{5}} + \frac{1}{x^{6}}} . \end{aligned}$

::f( x) g( x) = 2x3x6 - x2x6+x6 - 1x6x6x6x6x6 - 3x4x6 - 2x6+2x6+1x6=2x3 - 1x4+1x5 - 1x61 - 1x+3x2 - 2x5+1x6。

We observe that the limits $\begin{aligned} lim_{x \to \infty} f (x) \end{aligned}$ and $\begin{aligned} lim_{x \to \infty} g (x) \end{aligned}$ both exist. In particular, $\begin{aligned} lim_{x \to \infty} f (x) = 0 \end{aligned}$ and $\begin{aligned} lim_{x \to \infty} g (x) = 1 \end{aligned}$ . Hence Quotient Property now applies and we have
::我们注意到, limxf( x) 和 limxg( x) 的限值都存在。特别是, limxf( x) = 0 和 limxg( x) = 1 。因此, 数字属性现在适用, 我们已经使用。

$\begin{aligned} lim_{x \to \infty} \frac{2 x^{3} - x^{2} + x - 1}{x^{6} - x^{5} + 3 x^{4} - 2 x + 1} = \frac{0}{1} = 0. \end{aligned}$
::2x3 -x2+x1x6 -x5+3x4 -2x1=01=0。

Example 3
::例3

For the rational function $\begin{aligned} f (x) = \frac{x + 1}{x^{2} - 1} \end{aligned}$ , does $\begin{aligned} lim_{x \to 1} f (x) \end{aligned}$ exist?
::对于合理的函数 f( x) =x+1x2- 1, limx=1f( x) 存在吗 ?

We have the situation where the graph grows without bound on either side of $\begin{aligned} x = 1 \end{aligned}$ , in both a positive and a negative direction. There is a vertical asymptote at $\begin{aligned} x = 1 \end{aligned}$ . (There is a hole at $\begin{aligned} x = - 1 \end{aligned}$ .)
::图表在 x=1 的两侧无约束地生长, 向正方向和向负方向都有。在 x=1 时有一个垂直的静态( x\\ 1 时有一个洞) 。

In this example we note that $\begin{aligned} lim_{x \to 1} f (x) \end{aligned}$ does not exist , but the are:
::在这个例子中,我们注意到,limx1f(x)并不存在,但有:

$\begin{aligned} lim_{x \to 1^{-}} f (x) = - \infty \end{aligned}$ and $\begin{aligned} lim_{x \to 1^{-}} f (x) = + \infty \end{aligned}$ .
::=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

Example 4
::例4

Describe the end behavior of the graph. That is, determine if the function has a limit $\begin{aligned} L \end{aligned}$ , if the limit is infinite, or if the limit does not exist.
::描述图形的结束行为。也就是说, 确定函数是否有限制 L, 是否限制是无限的, 或者限制不存在。

$\begin{aligned} y = 2 (- 1)^{x} \end{aligned}$
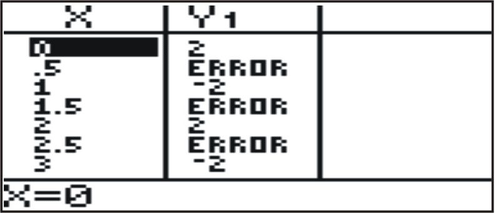
::y=2 (- 1) x

This function is difficult to understand without producing a graph. The table shows that the function only takes on two values: 2, and -2, and is undefined at non-integer values of $\begin{aligned} x \end{aligned}$ . As $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} + \infty \end{aligned}$ or $\begin{aligned} - \infty \end{aligned}$ , the function values alternate between 2 and -2. Therefore the limit does not exist.
::3⁄4 ̄ ̧漯B

Example 5
::例5

Describe the end behavior of the graph. That is, determine if the function has a limit $\begin{aligned} L \end{aligned}$ , if the limit is infinite, or if the limit does not exist.
::描述图形的结束行为。也就是说, 确定函数是否有限制 L, 是否限制是无限的, 或者限制不存在。

$\begin{aligned} y = 1 - \frac{1}{| x |} \end{aligned}$
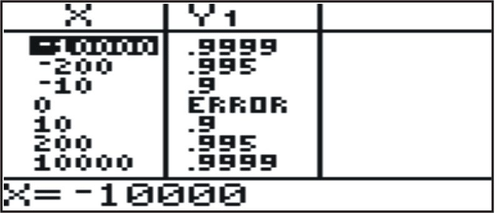
::y=1 - 1x

If you look at the table of this function, which has negative and positive values of $\begin{aligned} x \end{aligned}$ , you can see that as $\begin{aligned} x \end{aligned}$ approaches $\begin{aligned} + \infty \end{aligned}$ or $\begin{aligned} - \infty \end{aligned}$ , the function values approach 1.
::如果您查看此函数的表格,该表含有 x 的负值和正值,您可以看到,作为 x 接近 {{{} 或{} ,函数值取 1。

Therefore $\begin{aligned} lim_{x \to \infty} (1 - \frac{1}{| x |}) = lim_{x \to - \infty} (1 - \frac{1}{| x |}) = 1 \end{aligned}$ .
::因此, limx( 1 - 1 x) =limx( 1 - 1 x) = 1 。

We can also determine this limit analytically . For large values of $\begin{aligned} x \end{aligned}$ , $\begin{aligned} | x | \end{aligned}$ is also large, and so $\begin{aligned} \frac{1}{| x |} \end{aligned}$ is small (since dividing 1 by a large number results in a very small number). Therefore, for large values of $\begin{aligned} x \end{aligned}$ , $\begin{aligned} 1 - \frac{1}{| x |} \approx 1 - 0 = 1 \end{aligned}$ . We can make the same argument for x approaching $\begin{aligned} - \infty \end{aligned}$ .
::也可以用分析方式确定此限值。对于 x 的大值, x 也很大, 所以 1x 很小( 因为除以 1 以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一以一。对于 x 的大值, 我们可以为 x 的接近提出相同的论据。

Review
::回顾

Evaluate $\begin{aligned} lim_{x \to \infty} \frac{x^{3}}{x - 7} \end{aligned}$
::评估 limxx3x-7

Evaluate $\begin{aligned} lim_{x \to \infty} \frac{x^{2} + 2 x}{x - 3} \end{aligned}$
::评估 limxx2+2xx_3

Evaluate $\begin{aligned} lim_{x \to \infty} x^{3} \end{aligned}$
::评估 limxx3

Describe the end behavior of $\begin{aligned} y = 2 x^{2} + 3 x - 7 \end{aligned}$
::描述 y= 2x2+3x-7 的结束行为

Describe the end behavior of $\begin{aligned} y = - 2 x^{3} - 5 x^{2} + 8 x \end{aligned}$
::描述 y2x3 - 5x2+8x 的结束行为

In problems #6-12, find the limits if they exist.
::在问题6-12中,如果存在限制,请找到限制。

$\begin{aligned} lim_{x \to 3^{+}} \frac{(x + 2)^{2}}{(x - 2)^{2} - 1} \end{aligned}$
::立方厘米3+(x+2)2(x-2)2-2-2-1

$\begin{aligned} lim_{x \to \infty} \frac{(x + 2)^{2}}{(x - 2)^{2} - 1} \end{aligned}$
:x+2)(2(x-2)2-2-2-1)

$\begin{aligned} lim_{x \to 1^{+}} \frac{(x + 2)^{2}}{(x - 2)^{2} - 1} \end{aligned}$
:x+2)(2(x-2)2-2-2-2-1)

$\begin{aligned} lim_{x \to \infty} \frac{2 x - 1}{x + 1} \end{aligned}$
::limx%% 2x- 1x+1

$\begin{aligned} lim_{x \to - \infty} \frac{x^{5} + 3 x^{4} + 1}{x^{3} - 1} \end{aligned}$
::limx%x5+3x4+1x3-1

$\begin{aligned} lim_{x \to \infty} \frac{3 x^{4} - 2 x^{2} + 3 x + 1}{2 x^{4} - 2 x^{2} + x - 3} \end{aligned}$
::3x4 - 2x2+3x+12x4 - 2x2+x-3

$\begin{aligned} lim_{x \to \infty} \frac{2 x^{2} - x + 3}{x^{5} - 2 x^{3} + 2 x - 3} \end{aligned}$
::limx%2x2 - x+3x5 - 2x3+2x3 - 3

In problems #13-15, analyze the given function and identify all zeros, asymptotes and the end behavior of the graph.
::在问题13-15中, 分析给定函数, 并识别所有零、零、零和结束行为。

$\begin{aligned} f (x) = \frac{(x + 4)^{2}}{(x - 4)^{2} - 1} \end{aligned}$
:xx) = (x+4) 2(x-4) 2-2-1

$\begin{aligned} f (x) = - 3 x^{3} - x^{2} + 2 x + 2 \end{aligned}$
:x) 3x3 - x2+2x+2

$\begin{aligned} f (x) = \frac{2 x^{2} - 8}{x + 2} \end{aligned}$
:x)=2x2-8x+2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

涉及无限的限制

Limits Involving Infinity ::涉及无限的限制

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Limits Involving Infinity
::涉及无限的限制

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)