课程： 3.3 衍生物 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

衍生工具

Track star Becca decided that she needed a better way to figure out her instantaneous speed during her training runs than having her boyfriend Jim taking pictures of her at different parts of the run. She had an idea! She purchased a GPS receiver she could wear on her arm during her long training runs that would give her position data once per second that could be recorded on her laptop. She was determined to get good instantaneous speed data from the GPS recordings, and had a plan to do it.
::她想了个主意!她购买了一个GPS接收器,可以在她长期的训练中穿戴在手臂上,每秒一次提供她的位置数据。她决心从GPS记录中获取良好的即时速度数据,并计划这样做。

Can you figure out what Becca’s plan was?
::你能知道贝卡的计划是什么吗?

Becca successfully implemented her plan. On reviewing the laptop data from one of her long training runs, she saw the speed estimates go “haywire” during a 5 second time interval, before returning to normal values. Becca remembered running through a tunnel at the time.
::Becca成功地执行了她的计划。在审查她长期训练过程中的一台笔记本电脑数据时,她看到速度估计在5秒钟的间隔期间“电线”上升,然后恢复到正常值。 Becca记得当时在隧道里跑过。

Can you explain why Becca’s speed estimates went haywire?
::请解释为何贝卡的速率估计大幅下降?

The Derivative
::衍生工具

In the previous two concepts, the function $\begin{align*}f^{\prime}(x)\end{align*}$ was shown to represent two important characteristics of the function $\begin{align*}y=f(x)\end{align*}$ :
::在前两个概念中,F`(x)函数显示代表y=f(x)函数的两个重要特征:

The slope of the tangent line at $\begin{align*}x\end{align*}$ , and
::x 的正切线斜坡,以及

The instantaneous rate of change of $\begin{align*}y\end{align*}$ with respect to at $\begin{align*}x\end{align*}$ .
::xx时y的瞬时变化率。

These two characteristics of a function are so important that $\begin{align*}f^{\prime}(x)\end{align*}$ has it’s own name, the derivative .
::函数的这两个特性是如此重要,以致于F(x)有自己的名称,即衍生物。

The derivative of a function $\begin{align*}f(x)\end{align*}$ is the function $\begin{align*}f^{\prime}(x)\end{align*}$ whose value at $\begin{align*}x\end{align*}$ is given by
::函数 f(x) 的衍生函数 F(x) 是指以 x 值表示的函数 f*(x) 。

\begin{aligned} f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x)}{h} \end{aligned}

$\begin{align*}f^{\prime}(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\end{align*}$
::f_(x) = limh_0f(x+h) - f(x) h

provided that the limit exists.
::前提是存在限额。

The domain of $\begin{align*}f^{\prime}(x)\end{align*}$ consists of all the values of $\begin{align*}x\end{align*}$ for which the limit exists.
::f(x) 域包含有限制的 x 的所有值。

If the limit exists, and therefore the derivative, the function $\begin{align*}f(x)\end{align*}$ is said to be differentiable at $\begin{align*}x (x_0)\end{align*}$ .
::如果限制存在,因而衍生物也存在,则函数f(x)在 x(x0) 时表示函数f(x)是不同的。

Note: the following was also used to define $\begin{align*}f^{\prime}(x)\end{align*}$ :
::注:以下也用于界定f_(x):

\begin{aligned} f^{'} (x_{0}) = lim_{x \to x_{0}} \frac{f (x) - f (x_{0})}{x - x_{0}} \end{aligned}

$\begin{align*}f^{\prime}({x_0}) = \lim_{x \to x_0}\frac{f(x) - f(x_0)}{x - x_0}\end{align*}$
::f_(x0) = limx_x0f(x) - f(x0) x-x0

Calculus, just like all branches of mathematics, is rich with notation. There are many ways to denote the derivative of the function $\begin{align*}y = f(x)\end{align*}$ . Here are some of the ways:
::微积分和数学的所有分支一样,都有丰富的符号。有很多方法可以表示函数 y=f(x) 的衍生物。以下是一些方法:

\begin{aligned} f^{'} (x) \frac{d y}{d x} y^{'} \frac{d f}{d x} \frac{d f (x)}{d x} and D_{x} f (x) D_{x} y \end{aligned}

$\begin{align*}f^{\prime}(x) \qquad \frac{dy}{dx} \qquad y^{\prime} \qquad \frac{df}{dx} \qquad \frac{df(x)}{dx} \quad \text{and} \quad \ D_x f(x) \qquad D_xy\end{align*}$
::f_(x) dydxy_dfdxdf(x) dxxand Dxf(x) dxy

where the symbols $\begin{align*}\frac{d}{dx}\end{align*}$ and $\begin{align*}{D_x}\end{align*}$ are differential operators that act on the function to produce the derivative with respect to $\begin{align*}x\end{align*}$ .
::符号 ddx 和 Dx 是不同的操作员, 依函数作用产生相对于 x 的衍生物。

In addition, when substituting the point $\begin{align*}x_0\end{align*}$ into the derivative we denote the substitution by one of the following notations:
::此外,在将X0点替换为衍生物时,我们指用以下一个符号替代:

\begin{aligned} f^{'} (x_{0}) \frac{d y}{d x} | x - x_{0} \frac{d f}{d x} | x - x_{0} \frac{d f (x_{0})}{d x} \end{aligned}

$\begin{align*}f^{\prime}(x_0) \qquad \frac{dy}{dx}|x - x_0 \qquad \frac{df}{dx} \Bigg| x-x_0 \qquad \frac{df(x_0)}{dx}\end{align*}$
::{\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F(x0)\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F(x0)\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F2F(x0)

Apply the appropriate notation and find the equation of the tangent line to $\begin{align*}f(x)=\sqrt{x}\end{align*}$ at $\begin{align*}x_0=1\end{align*}$ .
::在 x0=1 时应用适当的符号, 并查找正切线的方程式为 f( x) =x 。

Using the definition of the derivative,
::使用衍生物的定义,

\begin{aligned} f^{'} (x) & = lim_{h \to 0} \frac{f (x + h) - f (x)}{h} \\ = lim_{h \to 0} \frac{\sqrt{x + h} - \sqrt{x}}{h} \\ = lim_{h \to 0} \frac{\sqrt{x + h} - \sqrt{x}}{h} \frac{\sqrt{x + h} + \sqrt{x}}{\sqrt{x + h} + \sqrt{x}} \\ = lim_{h \to 0} \frac{1}{h} \frac{x + h - x}{\sqrt{x + h} + \sqrt{x}} \\ = lim_{h \to 0} \frac{1}{\sqrt{x + h} + \sqrt{x}} \\ = \frac{1}{2 \sqrt{x}} . \end{aligned}

$\begin{align*}f^{\prime}(x) &=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h \to 0} \frac{\sqrt{x+h} - \sqrt{x}}{h} \\ &=\lim_{h \to 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}} \\ &= \lim_{h \to 0} \frac{1}{h} \frac{x+h-x}{\sqrt{x+h} + \sqrt{x}} \\ &= \lim_{h \to 0} \frac{1}{\sqrt{x+h} + \sqrt{x}} \\ &= \frac{1}{2 \sqrt{x}}.\end{align*}$
::f_(x) = limh_0f(x+h) - f(x) h= limh_0x+h-xx= limh_0xx+hx+hx+xxx+h+xx=limh_01x+h+h+x=limh_xx+h+h+x=limh_01x+h+x=12x。

Thus the slope of the tangent line at $\begin{align*}x_0=1\end{align*}$ is
::因此,x0=1时正切线的斜度是

\begin{aligned} f^{'} (1) = \frac{1}{2 \sqrt{1}} = \frac{1}{2} . \end{aligned}

$\begin{align*}f^{\prime}(1)=\frac{1}{2 \sqrt{1}}=\frac{1}{2}.\end{align*}$
::f(1)=121=12。

For $\begin{align*}x_0=1\end{align*}$ , we can find $\begin{align*}y_0\end{align*}$ by simply substituting into $\begin{align*}f(x)\end{align*}$ .
::对于 x0=1, 我们只需将 y0 替换为 f( x) 即可找到 y0 。

\begin{aligned} f (x_{0}) & \equiv y_{0} \\ f (1) & = \sqrt{1} = 1 \\ y_{0} & = 1. \end{aligned}

$\begin{align*}f(x_0) & \equiv y_0 \\ f(1) &= \sqrt{1}=1 \\ y_0 &= 1.\end{align*}$
::f( x0)\\\ y0f(1)=1=1=1y0=1。

Thus the equation of the tangent line is
::因此,正切线的方程式是

\begin{aligned} y - y_{0} & = m (x - x_{0}) \\ y - 1 & = \frac{1}{2} (x - 1) \\ y & = \frac{1}{2} x + \frac{1}{2} . \end{aligned}

$\begin{align*}y-y_0 &= m(x-x_0) \\ y-1 &= \frac{1}{2}(x-1) \\ y &= \frac{1}{2}x+\frac{1}{2}.\end{align*}$
::yy0=m(x-x0)y-1=12(x-1)y=12x+12。

Existence of the Derivative and Differentiability of a Function
::职能的衍生性和可区别性的存在

The above definition of the derivative of a function says that if the limit exists then the derivative exists at $\begin{align*}x\end{align*}$ , and the function is differentiable at $\begin{align*}x\end{align*}$ . If, at the point $\begin{align*}(x_0, f(x_0))\end{align*}$ , the limit does not exist , then the derivative of the function $\begin{align*}f(x)\end{align*}$ at this point does not exist either, and the function is not differentiable at $\begin{align*}x\end{align*}$ .
::函数的衍生物的上述定义表明,如果存在限制,则该衍生物存在于x,而该函数在x是不同的。如果在(x0,f(x0)x0)点不存在限制,那么此时函数f(x)的衍生物也不存在,且该函数在x是不可区别的。

The following are four cases where the derivative fails to exist.
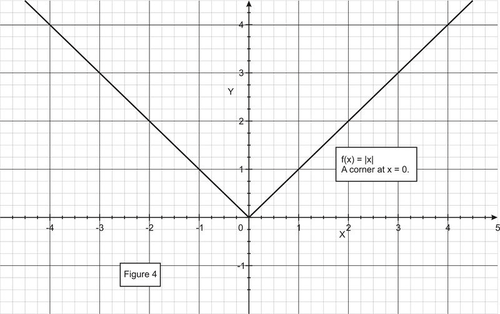
::以下是四例衍生物不存在的情况。

a. Derivative at a corner.
::a. 转角的衍生物。

Consider the function $\begin{align*}f(x) = |x|\end{align*}$ .
::考虑函数 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\ F( x)\\\\\\\\\\\\ 。

What is the derivative of $\begin{align*}f(x)\end{align*}$ at $\begin{align*}x_0=0\end{align*}$ ?
::x0=0时 f( x) 的衍生物是什么 ?

\begin{aligned} lim_{x \to x_{0}^{-}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = lim_{x \to 0^{-}} \frac{f (x) - f (0)}{x - 0} \\ = lim_{x \to 0^{+}} \frac{x}{x} & = - 1 \\ lim_{x \to x_{0}^{+}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = lim_{x \to 0^{+}} \frac{f (x) - f (0)}{x - 0} \\ = lim_{x \to 0^{+}} \frac{x}{x} & = 1 \end{aligned}

$\begin{align*}\lim_{x \to x_0{^-}} \frac{f(x)-f(x_0)}{x-x_0} &= \lim_{x \to 0{^-}}\frac{f(x)-f(0)}{x-0} \\ = \lim_{x \to 0{^+}} \frac{x}{x}& =-1\\ \lim_{x \to x_0{^+}}\frac{f(x)-f(x_0)}{x-x_0} &= \lim_{x \to 0{^+}}\frac{f(x)-f(0)}{x-0} \\ = \lim_{x \to 0{^+}} \frac{x}{x}& =1\end{align*}$
:

x)-f(x)-f(x0)x-x(x0)x-x0=limx0-f(x)-f(0)x-0(x)x-0(x)x(x)x(x)x(x)x(x)x(x)x0(x)+(f)x(x)x(x)x(x)x(x)x(x)x(x)x(x)x(x)x(x)x(x)x(x)x(x)x(0)x(x)x(0)x(0)x(0)x(0)x(0)x(0)x(0)x(0)x(x)x(x)=(x)xx(1)x(x)x(x)x)x(x)x(x)x(x)x)x(x)x(x)x(x)-f(x)-f(0)x)x(0)x(0)x(0)x)x(0(0)x)x)x(0(0(0)x)x)x(0(0(0)x)x)=(x(x)x)x(x)x(x)x)x)x(x(x)x)x(x)x)x)x(0(0(0)x)x)x(0)x(0)x(0)x(0(0)x(0)x(x(0)x)x(0)x)x(0)x)x(0)x(0)x(0)x)x(0)x(0)x(0)x(0)x)x(0)x(0)x)x)x(0)x(0)x(0(0)x(0)x(0)x(0)x(0)x(0(0)x)x)x(0)x(0)x)x)x)x(0)x)x)x(0(0)x(0)x(0)x(0)x(0)x(0)x(0)x(0

Since the limits on both sides of $\begin{align*}x=0\end{align*}$ are different, the derivative does not exist at $\begin{align*}x=0\end{align*}$ even though the function is continuous at $\begin{align*}x=0\end{align*}$ .
::由于x=0两侧的限制不同,即使函数在x=0时是连续的,衍生物在x=0时并不存在。

Corner: Both are finite, but different.
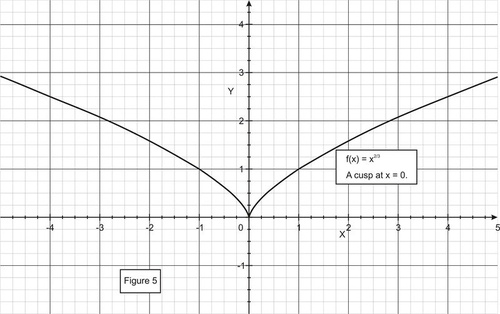
::角:两者都是有限的,但不同。

b. Derivative at a cusp.
::b. 孵化时的衍生物。

Consider the function $\begin{align*}f(x)=x^{\frac{2}{3}}\end{align*}$ .
::考虑函数 f( x) =x23 。

\begin{aligned} lim_{x \to x_{0}^{-}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = lim_{x \to 0^{-}} \frac{x^{\frac{2}{3}}}{x} \\ = lim_{x \to 0^{-}} x^{\frac{- 1}{3}} & = - \infty \\ and lim_{x \to x_{0}^{+}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = + \infty . \end{aligned}

$\begin{align*}\lim_{x \to x_0{^-}} \frac{f(x) - f(x_0)}{x - x_0}&= \lim_{x \to 0^-} \frac{x^{\frac{2}{3}}}{x}\\ = \lim_{x \to 0^-} x^{\frac{-1}{3}}&= - \infty \\ \text{and } \lim_{x \to x_0{^+}} \frac{f(x) - f(x_0)}{x - x_0}&= + \infty.\end{align*}$
::立方公尺xxxxxxxxxxxxxxx0xx0=limx0xxxx23x=limx_0-x-13}和limxxxxxxx0+f(x)-f(x0)x-x0xxxxxx0}。

Cusp: Both one-sided limits are infinite, but one is positive and the other is negative.
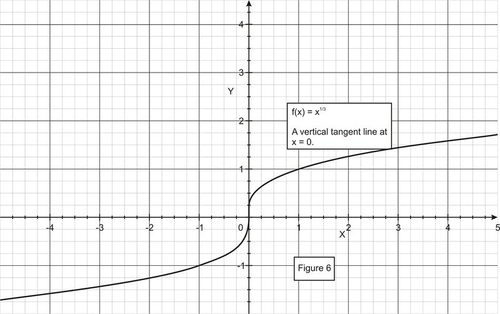
::Cusp: 两种单方面的限制都是无限的,但一种是积极的,另一种是消极的。

c. Derivative at a vertical tangent.
::c. 垂直正切的衍生物。

Consider the function $\begin{align*}f(x)=x^{\frac{1}{3}}\end{align*}$ .
::考虑函数 f( x) = x13 。

\begin{aligned} lim_{x \to x_{0}^{-}} \frac{f (x) - f (x_{0})}{x - x_{0}} = lim_{x \to 0^{-}} x^{\frac{- 2}{3}} = + \infty \\ lim_{x \to x_{0}^{+}} \frac{f (x) - f (x_{0})}{x - x_{0}} = lim_{x \to 0^{+}} x^{\frac{- 2}{3}} = + \infty \end{aligned}

$\begin{align*}\lim_{x \to x_0{^-}} \frac{f(x)-f(x_0)}{x-x_0}=\lim_{x \to 0^-}x^{\frac{-2}{3}}=+ \infty \\ \lim_{x \to x_0{^+}} \frac{f(x)-f(x_0)}{x-x_0}=\lim_{x \to 0^+}x^{\frac{-2}{3}}=+ \infty \end{align*}$
::立方公尺xxxxxxxxxxx0-f(x)-f(x0)xx-xxxx-x0=limx0x0-x-x-x-x-xxxxxxxxxxxx0+f(x)-f(x0)xx-x0-x0=limx_0x-x-23}

Because the limits on both sides of $\begin{align*}x=0\end{align*}$ are infinity, the derivative does not exist at $\begin{align*}x=0\end{align*}$ even though the function is continuous at $\begin{align*}x=0\end{align*}$ .
::由于 x=0 的两侧的限值都是无限的,因此即使函数在 x=0 时是连续的,衍生物在 x=0 时并不存在。

Vertical tangent: Both one-sided limits at $\begin{align*}x=a\end{align*}$ are $\begin{align*}+ \infty\end{align*}$ .
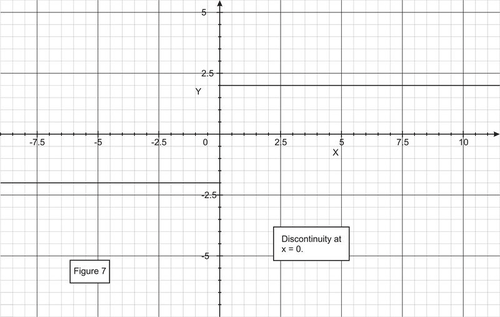
::垂直切切: x=a 的两侧限制都是。

d. Derivative at a jump discontinuity.
::d. 跳跃不连续的衍生物。

Consider the step function
::考虑职档函数

\begin{aligned} f (x) = {\begin{cases} - 2, x < 0 \\ 2, x \geq 0 \end{cases} \end{aligned}

$\begin{align*}f(x) = \begin{cases} -2, \quad \ x<0 \\ 2, \qquad x \ge 0 \end{cases}\end{align*}$
::f(x)%% 2, x < 02, x% 0

\begin{aligned} lim_{x \to x_{0}^{-}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = lim_{x \to 0^{-}} \frac{- 2 - 2}{x} = + \infty \\ lim_{x \to x_{0}^{+}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = lim_{x \to 0^{+}} \frac{2 - 2}{x} = 0 \end{aligned}

$\begin{align*}\lim_{x \to x_0^-} \frac{f(x)-f(x_0)}{x-x_0} &= \lim_{x \to 0^-} \frac{-2 -2}{x}=+ \infty \\ \lim_{x \to x_0^+} \frac{f(x)-f(x_0)}{x-x_0} &= \lim_{x \to 0^+} \frac{2 -2}{x}=0 \\\end{align*}$
::立方公尺xxxxxxxxxxxxxxxxxxxxxxxxxxxx0-f(x)xxxxxxxxxxxxxxxx0-x(x)xxxxxxxxxxxxxxxxxxxxxx-x-x0-x0=lxxxxxxxxxxxxxxxxxxxxx_0+2-2xx=0 =2xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx0xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

Since the limits on both sides of $\begin{align*}x=0\end{align*}$ are different, the derivative does not exist at $\begin{align*}x=0\end{align*}$ even though the function is defined at $\begin{align*}x=0\end{align*}$ . But the function is not continuous at $\begin{align*}x=0\end{align*}$ .
::由于 x=0 的两侧的限值不同,即使函数在 x=0 时被定义,衍生物在 x=0 时并不存在。但函数在 x=0 时不是连续的。

Jump discontinuity: Both one-sided limits are different and the function is not continuous at $\begin{align*}x=a\end{align*}$ .
::跳动不连续性:单向限制不同,在 x=a 时函数不连续。

Differentiability and Continuity
::差异性和连续性

The cases above show that a function may or may not have a derivative at a particular value of $\begin{align*}x\end{align*}$ , i.e., the function may or may not be differentiable at $\begin{align*}x\end{align*}$ . Cases a-c above show that not every continuous function is differentiable. But in all cases we have examined, when the derivative exists, the function is continuous at the point the derivative is being evaluated. We have not seen any cases where the derivative exists and the function is not continuous. Are there any such cases? The answer is no. This fact is expressed by the following theorem, one of the most important theorems in calculus:
::上述案例表明,一个函数在x的某个特定值上可能具有或可能没有衍生物,即该函数在x的某个值上可能具有或可能不具有差异。上文a-c案件表明,并非所有连续函数都是不同的。但在所有案例中,当衍生物存在时,在对衍生物进行评价时,该函数是连续的。我们没有看到任何衍生物存在且函数不连续的情况。是否有任何这类情况?答案是否定的。这一事实由以下的词标来表达,这是计算中最重要的词标之一:

If $\begin{align*}f\end{align*}$ is differentiable at $\begin{align*}x_0\end{align*}$ , then $\begin{align*}f\end{align*}$ is also continuous at $\begin{align*}x_0\end{align*}$ .
::如果 f 在 x0 时是可变的, f 在 x0 时也是连续的。

Note the equivalent: If $\begin{align*}f\end{align*}$ is not continuous at $\begin{align*}x_0\end{align*}$ , then $\begin{align*}f\end{align*}$ is not differentiable at $\begin{align*}x_0\end{align*}$ .
::注等值:如果 f 在x0 时不连续,那么 f 在 x0 时是不可区分的。

We have already seen that the converse is not true in some cases. The function can have a cusp, a corner, or a vertical tangent and still be continuous, but is not differentiable.
::我们已经看到,在某些情况中,反之亦然。函数可以有一个角、一个角或垂直正切,并且仍然是连续的,但不可区别。

Using the derivative, give an argument for why the function $\begin{align*}f(x) = x^2\end{align*}$ is continuous at $\begin{align*}x = -5\end{align*}$ .
::使用衍生物,请说明为什么函数 f( x) =x2 在 x @ @ 5 时是连续的。

Using the definition of the derivative:
::使用衍生品的定义:

\begin{aligned} f^{'} (x) & = lim_{x \to - 5} \frac{(x + h)^{2} - x^{2}}{h} \\ = lim_{h \to 0} \frac{x^{2} + 2 x h + h^{2} - x^{2}}{h} \\ = lim_{h \to 0} \frac{2 x h + h^{2}}{h} \\ = lim_{h \to 0} (2 x + h) \\ = 2 x \end{aligned}

$\begin{align*}f^{\prime}(x) &= \lim_{x \to -5} \frac{(x+h)^2 - x^2}{h} \\ &= \lim_{h \to 0} \frac{x^2+2xh+h^2-x^2}{h} \\ &= \lim_{h \to 0} \frac{2xh+h^2}{h} \\ &= \lim_{h \to 0}(2x+h) \\ &= 2x\end{align*}$
::f_(x) = limx%5 (x+h) 2 -x2h= limh0x2+2x2xx2+2xh2 -x2h= limh= 02xh+h2h=limh0(2x+h)=2x

Thus, $\begin{align*}f^{\prime}(-5)=2(-5)=-10\end{align*}$ . Because $\begin{align*}f(x)=x^2\end{align*}$ is differentiable at $\begin{align*}x=-5\end{align*}$ , $\begin{align*}f(x)\end{align*}$ is continuous at $\begin{align*}x=-5\end{align*}$ .
::因此, f`( - 5) = 2( - 5) =10。因为 f( x) =x2 在 x* 5 时是不同的, f( x) =x2 在 x * 5 时是连续的。

Examples
::实例

Example 1
::例1

Earlier, you were asked about Becca's plan to determine her instantaneous running speed by using a GPS receiver to send once-per-second position signals to her laptop. Did you figure out her plan?
::早些时候,有人问及贝卡计划使用GPS接收器向她的笔记本电脑发送每秒一次定位信号,以确定她的即时运行速度。

Becca knew that the recorded GPS position data could be used to determine how far she had run at any time. She was able to use a laptop program to accurately model these running distance versus time estimates with a mathematical function. Using her recent knowledge of derivatives, Becca was able to determine her speed at any time by computing the derivative of the math function. It worked really well!
::Becca知道,所记录的GPS定位数据可以用来确定她任何时候都跑多远。她能够使用笔记本电脑程序用数学函数来精确模拟这些运行距离和时间估计。 Becca利用她最近对衍生物的了解,能够随时通过计算数学函数的衍生物来确定她的速度。它非常有效 !

But what happened to cause the 5-seconds of “haywire” results?
::但导致5秒“电网”结果的原因又是什么?

Becca soon came to the realization that she lost GPS position data during her run in the tunnel because it blocked receiving the signal. The math model of distance vs time was therefore discontinuous during the 5-second interval (jump discontinuity?), and the speed estimate (derivative) during the time was not reliable.
::Becca很快意识到,她在隧道里运行时失去了GPS定位数据,因为它阻止了接收信号。因此,距离和时间的数学模型在5秒间隔(跳跃不连续? ) 期间不连续,而当时的速度估计(衍生的)并不可靠。

Example 2
::例2

Find the derivative of $\begin{align*}f(x) = \frac{x}{{x + 1}}\end{align*}$ at $\begin{align*}x=0\end{align*}$ and $\begin{align*}x=-1\end{align*}$ ; use the results to say something about the continuity of $\begin{align*}f(x)\end{align*}$ at those points.
::查找 f( x) =xx+1 在 x=0 和 x1 上的衍生物; 使用结果来表示 f( x) 在这些点的连续性。

We begin with the definition of the derivative,
::我们从衍生物的定义开始

\begin{aligned} f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x)}{h} = lim_{h \to 0} \frac{1}{h} [f (x + h) - f (x)], \end{aligned}

$\begin{align*}f^{\prime}(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\frac{1}{h} [f(x+h)-f(x)],\end{align*}$
::f_(x) = limh_0f(x+h) - f(x) h=limh_01h[f(x+h) - f(x)],

where
::何地

\begin{aligned} f (x) & = \frac{x}{x + 1} \\ f (x + h) & = \frac{x + h}{x + h + 1} \end{aligned}

$\begin{align*}f(x) &= \frac{x}{x+1} \\ f(x+h) &= \frac{x+h}{x+h+1}\end{align*}$
::f(x) =xx+1f(x+h) =x+hx+h+1

Substituting into the derivative formula,
::替代衍生物公式,

\begin{aligned} f^{'} (x) & = lim_{h \to 0} \frac{1}{h} [\frac{x + h}{x + h + 1} - \frac{x}{x + 1}] \\ = lim_{h \to 0} \frac{1}{h} [\frac{(x + h) (x + 1) - x (x + h + 1)}{(x + h + 1) (x + 1)}] \\ = lim_{h \to 0} \frac{1}{h} [\frac{x^{2} + x + h x + h - x^{2} - x h - x}{(x + h + 1) (x + 1)}] \\ = lim_{h \to 0} \frac{1}{h} [\frac{h}{(x + h + 1) (x + 1)}] \\ = lim_{h \to 0} \frac{1}{(x + h + 1) (x + 1)} \\ = \frac{1}{(x + 1)^{2}} . \end{aligned}

$\begin{align*}f^{\prime}(x) &= \lim_{h \to 0} \frac{1}{h} \left[\frac{x+h}{x+h+1} - \frac{x}{x+1}\right] \\ &= \lim_{h \to 0} \frac{1}{h} \left[\frac{(x+h)(x+1) - x(x+h+1)}{(x+h+1)(x+1)}\right] \\ &= \lim_{h \to 0} \frac{1}{h}\left[\frac{x^2+x+hx+h-x^2-xh-x}{(x+h+1)(x+1)}\right] \\ &= \lim_{h \to 0} \frac{1}{h} \left[\frac{h}{(x+h+1)(x+1)}\right] \\ &= \lim_{h \to 0}\frac{1}{(x+h+1)(x+1)} \\ &= \frac{1}{(x+1)^2}. \end{align*}$
::f{(x) =limh+hx+hx+h+h1+1=limh#01h}[(x+h)(x+h)(x+1)(x+h+1)(x+1)] =limh+h+1[x2+x+hx+hx+xxxxxxx(x+h+1)(x+1)(1)] =limh+01h[h(x+h+1)(x+1)] =limh_01(x+h+1)(x+1)(x+1)(x+1)(x+1)(x+1) =1(x+1)。

Evaluating the derivative at $\begin{align*}x=0\end{align*}$ : $\begin{align*}f^{\prime}(0) = 1\end{align*}$ . Because the function is differentiable at $\begin{align*}x=0\end{align*}$ , the function is continuous at $\begin{align*}x=0\end{align*}$ .
::在 x=0 : f( 0) =1. 由于函数在 x=0 时是不同的, 函数在 x=0 时是连续的。

Evaluating the derivative at $\begin{align*}x=-1\end{align*}$ : $\begin{align*}f^{\prime}(-1) = \infty\end{align*}$ . Because the function is not differentiable at $\begin{align*}x=-1\end{align*}$ , the function is not continuous at $\begin{align*}x=-1\end{align*}$ .
::在 x1 : f(- 1)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\没有差异的衍生物的函数。因为函数是不可区别的\ d\\\\\\ d\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Review
::回顾

In #1-6, use the definition of the derivative to find $\begin{align*}f^{\prime}(x)\end{align*}$ and then find the equation of the tangent line at $\begin{align*}x=x_0\end{align*}$ .
::在 # 1-6 中, 使用衍生物的定义查找 f_ (x) , 然后在 x=x0 找到正切线的方程式。

$\begin{align*}f(x)=6x^2\end{align*}$ ; $\begin{align*}x_0=3\end{align*}$
:xx) = 6x2; x0= 3

$\begin{align*}f(x)=\sqrt{x+2}\end{align*}$ ; $\begin{align*}x_0=8\end{align*}$
::f( x) =x+2; x0=8

$\begin{align*}f(x)=3x^3 -2\end{align*}$ ; $\begin{align*}x_0=-1\end{align*}$
:x)=3x3-2; x01

$\begin{align*} f(x)=\frac{1}{x+2}\end{align*}$ ; $\begin{align*}x_0=-1\end{align*}$
:x) = 1x+2; x0 @% 1

$\begin{align*}f(x)=ax^2-b\end{align*}$ , (where $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are constants); $\begin{align*}x_0=b\end{align*}$
::f( x) = 轴 - b, (a和b为常数); x0=b

$\begin{align*}f(x)=x^{\frac{1}{3}}\end{align*}$ ; $\begin{align*}x_0=1\end{align*}$
:xx) =x13; x0=1

Find $\begin{align*}\frac{dy}{dx} \big |_{x=1}\end{align*}$ given that $\begin{align*}y=5x^2-2\end{align*}$ .
::根据 y= 5x2 - 2 来查找 dydxx=1 。

Show that $\begin{align*}f(x)=\sqrt[3]{x}\end{align*}$ is continuous at $\begin{align*}x=0\end{align*}$ but it is not differentiable at $\begin{align*}x=0\end{align*}$ . Sketch the graph.
::显示 f( x) =x3 在 x=0 时是连续的, 但是在 x=0 时是无法区分的。拖曳图形。

Show that $\begin{align*}f(x)=\begin{cases} x^2+1 & x \ge 1 \\ 2x & x > 1 \end{cases}\end{align*}$ is continuous and differentiable at $\begin{align*}x=1\end{align*}$ . Sketch the graph of $\begin{align*}f\end{align*}$ .
::显示 f( x) % x2+1x12xx > 1 在 x= 1 时是连续和可区分的。拖曳 f 的图形。

Use the definition of derivative to calculate the derivative of $\begin{align*}f(x)=2x^2+x\end{align*}$ at $\begin{align*}x=2\end{align*}$ .
::使用衍生物的定义来计算 f( x) = 2x2+x 的衍生物 x=2 。

Write the formula for the derivative of $\begin{align*}f(x) = 3(x - 1)^2 + 7\end{align*}$
::写入 f( x) =3( x- 1) 2+7 衍生物的公式

Find the formula for the derivative of $\begin{align*}f(x)=\sqrt{x-1}\end{align*}$
::查找 f( x) =x- 1 的衍生物的公式

Use the definition of derivative to calculate the derivative of $\begin{align*}f(x) = \sqrt{6 - 2x}\end{align*}$ at $\begin{align*}x=-5\end{align*}$ .
::使用衍生物的定义来计算 f( x) =6 - 2x 的衍生物。

Find the formula for the derivative of $\begin{align*}f(x) = \frac{1}{x + 1}\end{align*}$ .
::查找 f( x) = 1x+1 的衍生物的公式。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

衍生工具

The Derivative ::衍生工具

Existence of the Derivative and Differentiability of a Function ::职能的衍生性和可区别性的存在

Differentiability and Continuity ::差异性和连续性

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Review ::回顾

Review (Answers) ::回顾(答复)