Course: 4.10 职能的线性化

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

函数的线条化

Suppose you absolutely needed to know the value of the square root of 19 but all you had was pencil and paper, no calculator. Could you calculate it? With your current understanding of the derivative as the slope of a tangent line, you should be able to. Try computing $\begin{aligned} \sqrt{19} \end{aligned}$ without a calculator; then compare your result with this concepts method of linearization and a calculator.
::假设你绝对需要知道 19 的平方根值, 但您所拥有的只是铅笔和纸, 没有计算器。您能否计算它 ? 您目前对衍生物作为正切线的斜坡有了解, 您应该能够这样做。尝试在没有计算器的情况下计算 19 ; 然后将您的结果与这种直线化和计算器的概念方法进行比较。

Linearization
::线性

Linearization of a function means using the tangent line of a function at a point as an approximation to the function in the vicinity of the point. This relationship between a tangent and a graph at the point of tangency is often referred to as local linearization.
::函数的线条化是指在某点使用函数的正切线条作为接近点附近函数的近似值。正切线和正切点的图形之间的关系通常称为局部线条化。

Given the function $\begin{aligned} f (x) \end{aligned}$ and the derivative $\begin{aligned} f^{'} (x) \end{aligned}$ , the tangent line at a point $\begin{aligned} x_{0} \end{aligned}$ can be written in point-slope form as:
::根据函数 f(x) 和衍生函数 f_(x), 点 x0 的正切线可以写成点斜体, 如下:

\begin{aligned} y - f (x_{0}) = f^{'} (x_{0}) (x - x_{0}) or y = f (x_{0}) + f' (x_{0}) (x - x_{0}) \end{aligned}

.
::yf(x0) = f}(x0) (x0) (x-x0) 或y= f(x0) +f* (x0) (x-x0) 。

If we consider that this tangent line is a good approximation to $\begin{aligned} f (x) \end{aligned}$ in the vicinity of $\begin{aligned} x_{0} \end{aligned}$ , we can write
::如果我们认为这条正切线与x0附近f(x)相当近似,我们可以写

$\begin{aligned} f (x) \approx y = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) \end{aligned}$ . This is the linearization of $\begin{aligned} f (x) \end{aligned}$ about $\begin{aligned} x_{0} \end{aligned}$ .
::f(x) y=f(x0) +f*(x0)(x) -xx0。这是f(x) 的线性化, 大约x0 。

The tangent line as the local linearization of $\begin{aligned} f (x) \end{aligned}$ is often designated $\begin{aligned} L (x) \end{aligned}$ , so that
::f(x) 的本地线直线化的正切线条通常被指定为 L(x),因此

\begin{aligned} f (x) \approx L (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) . \end{aligned}

xx) L(x) = f(x0) +f*(x0)(x) -x0。

Take the function $\begin{aligned} f (x) = x^{2} - 2 x - 3 \end{aligned}$ and find the linearization at the points $\begin{aligned} x_{0} = 1.5 \end{aligned}$ and $\begin{aligned} x_{0} = - 0.5 \end{aligned}$ .
::将函数 f(x) =x2- 2x- 3 带到 x0=1.5 和 x00. 5 点处找到线性化。

The linearization of $\begin{aligned} f (x) \end{aligned}$ is given by: $\begin{aligned} f (x) \approx f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) \end{aligned}$ .
::f( x) 的线性化由 : f( x)\\\ f( x0) + f*( x0) (x) - x0 ) 给出。

We have:
::我们已:

$\begin{aligned} f (1.5) = - 3.75 \end{aligned}$ and $\begin{aligned} f (- 0.5) = - 1.75 \end{aligned}$
::f(1.5) 3.75 和 f(-0.5) 1.75

$\begin{aligned} f^{'} (x) = 2 x - 2 \end{aligned}$ , so that $\begin{aligned} f^{'} (1.5) = 1 \end{aligned}$ and $\begin{aligned} f^{'} (- 0.5) = - 3 \end{aligned}$ .
::f_(x)=2x-2,所以f_(1.5)=1和f_(-05)=3。

The linearization becomes:
::线性化变成:

\begin{aligned} At x_{0} = - 0.5 At x_{0} = 1.5 \\ f (x) & \approx - 1.75 - 3 (x + 0.5) \approx - 3.75 + (x - 1.5) \\ \approx - 3 x - 3.25 \approx x - 5.25 \end{aligned}

::在 x0 % 0.5At x0=1.5f(x) 1. 75-3(x+0.5) 3. 75+(x-1.5) 3x-3.25 x-5.25

As the figure illustrates and the table shows, as we move away from $\begin{aligned} x_{0} \end{aligned}$ , we lose accuracy.
::如图所示和表格所示,随着我们远离x0,我们失去了准确性。

Error near $\begin{aligned} x_{0} = - 0.5 \end{aligned}$				Error near $\begin{aligned} x_{0} = 1.5 \end{aligned}$
$\begin{aligned} x \end{aligned}$	$\begin{aligned} f (x) \end{aligned}$	$\begin{aligned} - 3 x - 3.25 \end{aligned}$	\|True-Approx\|	$\begin{aligned} x \end{aligned}$	$\begin{aligned} f (x) \end{aligned}$	$\begin{aligned} x - 5.25 \end{aligned}$	\|True-Approx\|
-1	0	-0.25	0.25	1.0	-4	-4.25	0.25
-0.5	-1.75	-1.75	0.00	1.5	-3.75	-3.75	0.00
0	-3	-3.25	0.25	2.0	-3.25	-3.00	0.25

Examples
::实例

Example 1
::例1

Earlier, you were asked to first try computing $\begin{aligned} \sqrt{19} \end{aligned}$ without a calculator and then to compare your result with this concepts method of linearization and a calculator.
::早些时候,你被要求首先尝试计算19,不用计算器,然后将你的结果与这种线性化和计算器的概念方法进行比较。

Congratulations if you were able to linearize $\begin{aligned} \sqrt{x} \end{aligned}$ at $\begin{aligned} x = 16 \end{aligned}$ ( or $\begin{aligned} x = 25 \end{aligned}$ ).
::如果您能够将 x=16 (或 x=25) x 线性化, 恭喜。

The linearization is $\begin{aligned} y = \frac{1}{8} (x - 16) + 4 \end{aligned}$ , which means $\begin{aligned} y = 4.375 \end{aligned}$ when $\begin{aligned} x = 19 \end{aligned}$ . A calculator would give 4.359.
::线性化为y=18(x-16)+4,这意味着在 x=19时y=4.375。计算器将给出4.359。

Example 2
::例2

Find the linearization of $\begin{aligned} f (x) = \sqrt{x + 3} \end{aligned}$ at point $\begin{aligned} x = - 1 \end{aligned}$ .
::在点 x% 1 查找 f( x) =x+3 的线性化。

We have:
::我们已:

$\begin{aligned} f (1) = 2 \end{aligned}$ , and
::f(1)=2, 和

$\begin{aligned} f^{'} (x) = \frac{1}{2} (x + 3)^{- \frac{1}{2}} \end{aligned}$ , so that $\begin{aligned} f^{'} (1) = \frac{1}{4} \end{aligned}$ .
::f*(x)=12(x+3)-12,因此f(1)=14。

The linearization becomes:
::线性化变成:

\begin{aligned} f (x) & \approx 2 + \frac{1}{4} (x - 1) \\ \approx \frac{1}{4} x + \frac{7}{4} \end{aligned}

::f( x) @% 2+14( x- 1) @% 14x+74

This tells us that near the point $\begin{aligned} x = 1 \end{aligned}$ , the function $\begin{aligned} f (x) = \sqrt{x + 3} \end{aligned}$ approximates the line $\begin{aligned} y = (\frac{x}{4}) + \frac{7}{4} \end{aligned}$ . As the figure illustrates and the table shows, as we move away from $\begin{aligned} x = 1 \end{aligned}$ , we lose accuracy.
::这告诉我们,在X=1点附近,函数f(x)=x+3 接近y=(x4)+74。如图所示和表格所示,当我们从 x=1 移动时,我们失去准确性。

$\begin{aligned} x \end{aligned}$	$\begin{aligned} f (x) \end{aligned}$	$\begin{aligned} \approx \frac{1}{4} x + \frac{7}{4} \end{aligned}$	\|True-Approx\| ::
1	2	2	0
1.5	2.121	2.125	0.004
2	2.236	2.25	0.014
3	2.449	2.5	0.41

Example 3
::例3

Find the linearization of $\begin{aligned} y = \sin x \end{aligned}$ at $\begin{aligned} x = \frac{π}{3} \end{aligned}$ .
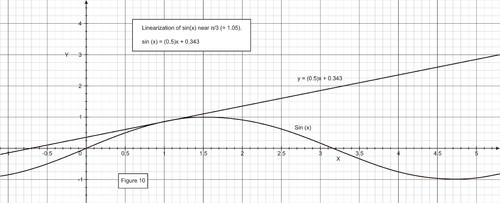
::在 x3 中查找 y=sinx 的线性化。

The linearization of $\begin{aligned} f (x) \end{aligned}$ is given by: $\begin{aligned} f (x) \approx f (x_{0}) + f' (x_{0}) (x - x_{0}) \end{aligned}$ .
::f( x) 的线性化由 : f( x)\\\ f( x0) + f*( x0) (x) - x0 ) 给出。

We have
::我们有

$\begin{aligned} f (\frac{π}{3}) = \sin (\frac{π}{3}) = \frac{\sqrt{3}}{2} \end{aligned}$ , and
::f( 3) =sin ( 3) = 32, 和

$\begin{aligned} f^{'} (x) = \cos x \end{aligned}$ , so that $\begin{aligned} f^{'} (\frac{π}{3}) = \cos (\frac{π}{3}) = \frac{1}{2} \end{aligned}$ .
::f_(x) = cosx, 所以 f_ 3 = cos { 3) = 12。

The linearization becomes:
::线性化变成:

\begin{aligned} f (x) & \approx \frac{\sqrt{3}}{2} + \frac{1}{2} (x - \frac{π}{3}) \\ \approx \frac{\sqrt{3}}{2} + \frac{x}{2} - \frac{π}{6} \\ \approx \frac{x}{2} + 0.342 \end{aligned}

::f( x)\\\\\\\\\\\\\\\\\\\\\\\\12\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\+12\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\12\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\0. 342+0. 342

Example 4
::例4

Let $\begin{aligned} f \end{aligned}$ be a function such that $\begin{aligned} f (5) = 6 \end{aligned}$ and whose derivative is $\begin{aligned} f^{'} (x) = \sqrt{x^{3} + 44} \end{aligned}$ . Approximate $\begin{aligned} f (5.3) \end{aligned}$ .
::使 f 成为 f(5)=6 的函数, 其衍生物为 f_( x) =x3+44。近似 f( 5. 3) 。

Since we have $\begin{aligned} f (5) = 6 \end{aligned}$ , let $\begin{aligned} x_{0} = 5 \end{aligned}$ .
::因为我们有f(5)=6, let x0=5。

Then $\begin{aligned} f^{'} (x_{0}) = \sqrt{x_{0}^{3} + 44} = \sqrt{169} = 13 \end{aligned}$
::然后f_(x0)=x03+44=169=13

The linearization becomes:
::线性化变成:

\begin{aligned} f (x) & \approx 6 + 13 (x - 5) \\ f (5.3) & \approx 6 + 13 (5.3 - 5) \\ \approx 6 + 13 (0.3) \\ \approx 9.9 \end{aligned}

::f(x)6+13(x-5)f(5.3)6+13(5.3-5)_6+13(0.3)_9

Review
::回顾

Find the linearization of $\begin{aligned} f (x) = \frac{x^{2} + 1}{x} \end{aligned}$ , $\begin{aligned} x_{0} = 1 \end{aligned}$ , $\begin{aligned} f (1.7) \end{aligned}$
::查找 f( x) =x2+1x, x0=1, f( 1. 7) 的线性化

Find the linearization of $\begin{aligned} f (x) = \tan x \end{aligned}$ at $\begin{aligned} a = π \end{aligned}$ .
::查找 f( x) =tanx 的线性化。

Use the result of problem #3, $\begin{aligned} (1 + x)^{n} \approx 1 + n x \end{aligned}$ , to find the approximation for the following:
1. $\begin{aligned} f (x) = (1 - x)^{4} \end{aligned}$
  :fx) =(1-x) 4
2. $\begin{aligned} f (x) = \sqrt{1 - x} \end{aligned}$
  :xx)=1-x
3. $\begin{aligned} f (x) = \frac{5}{\sqrt{1 + x}} \end{aligned}$
  :xx)=51+x
4. $\begin{aligned} f (x) = \sqrt[3]{{(1 - \frac{3}{(x - 1)})}^{2}} \end{aligned}$
  :fx) = (1- 3(x-1)) 23
5. Without using a calculator, approximate $\begin{aligned} (1.003)^{99} \end{aligned}$ .
  ::未使用计算器,约为1.00399。
::使用问题3的结果, (1+x) n%1+nx) 来找到以下各项的近似值: f(x) = (1-x) = (1-x) 4 f(x) = 1- x f(x) = 51+x f(x) = (1- 3(x-1) ) 23 , 不使用计算器, 大约 (1.00399) 。

For #5 - 13, find the linearization of the given function at the given point x ₀ and use this approximation to compute the given quantity. Compare the result to the value obtained by calculator; compute the error.
::对于 # 5 - 13, 在给定点 x0 找到给定函数的线性化, 并使用此近似值来计算给定数量。比较计算结果和通过计算获得的值; 计算错误。

$\begin{aligned} f (x) = 1 + \sin x \end{aligned}$ , $\begin{aligned} x_{0} = 0 \end{aligned}$ , $\begin{aligned} f (0, 3) \end{aligned}$
::f( x) = 1+sinx, x0=0, f( 0. 3)

$\begin{aligned} f (x) = \sqrt{1 + x} \end{aligned}$ , $\begin{aligned} x_{0} = 0 \end{aligned}$ , $\begin{aligned} \sqrt{1.006} \end{aligned}$
::f(x)=1+x,x0=0,1.006

$\begin{aligned} f (x) = (1 + x)^{10} \end{aligned}$ , $\begin{aligned} x_{0} = 0 \end{aligned}$ , $\begin{aligned} {1.02}^{10} \end{aligned}$
::f(x) =(1+x) 10, x0= 0, 1.0210

$\begin{aligned} f (x) = \frac{1}{\sqrt{x + 1}} \end{aligned}$ , $\begin{aligned} x_{0} = 0 \end{aligned}$ , $\begin{aligned} \frac{1}{\sqrt{0.885}} \end{aligned}$
::f(x) = 1x+1, x0=0, 10.885

$\begin{aligned} f (x) = x^{2} - 3 x + 10 \end{aligned}$ , $\begin{aligned} x_{0} = 3 \end{aligned}$ , $\begin{aligned} f (3.65) \end{aligned}$
::f( x) =x2-3x+10, x0=3, f( 3. 65)

$\begin{aligned} f (x) = x^{3} + 2 \end{aligned}$ , $\begin{aligned} x_{0} = 3 \end{aligned}$ , $\begin{aligned} f (3.3) \end{aligned}$
::f(x) =x3+2, x0=3, f(3.3)

$\begin{aligned} f (x) = \frac{1}{x^{2}} \end{aligned}$ , $\begin{aligned} x_{0} = 2 \end{aligned}$ , $\begin{aligned} \frac{1}{{2.03}^{2}} \end{aligned}$
::f(x) = 1x2, x0= 2, 12.032

$\begin{aligned} f (x) = e^{x} \end{aligned}$ , $\begin{aligned} x_{0} = 0 \end{aligned}$ , $\begin{aligned} e^{0.2} \end{aligned}$
::f(x) =ex, x0=0, e0. 2

For #13 - 14, estimate the following numbers and determine the error:
::对于 #13-14, 估计以下数字并确定错误 :

Approximate $\begin{aligned} \sqrt[4]{628} \end{aligned}$
::近似6284

Estimate the value of $\begin{aligned} \frac{1}{2.007} \end{aligned}$
::估计价值12 007美元

Let $\begin{aligned} f \end{aligned}$ be a function such that $\begin{aligned} f (1) = 2 \end{aligned}$ and whose derivative is $\begin{aligned} f^{'} (x) = \sqrt{x^{3} + 1} \end{aligned}$ . Approximate $\begin{aligned} f (1.3) \end{aligned}$ .
::使 f 成为 f(1)=2 的函数, 其衍生物为 f_( x) =x3+1. 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

函数的线条化

Linearization ::线性

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Linearization
::线性

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)