5.1 抗排除剂和无限期综合

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节和无限期综合综合

  折叠 展开

  和无限期综合综合

  播放段落

  You have spent many lessons learning about how to find the derivative, $\begin{align*}f^\prime(x)\end{align*}$ , of a function $\begin{align*}f(x)\end{align*}$ , and the process of differentiation. It should be no  surprise then that there would be a name for the function $\begin{align*}f(x)\end{align*}$ , or family of functions, that can generate $\begin{align*}f^\prime(x)\end{align*}$ when differentiated: $\begin{align*}f(x)\end{align*}$ and  $\begin{align*}f^\prime(x)\end{align*}$ are a pair of , and $\begin{align*}f(x)\end{align*}$ is called an antiderivative of $\begin{align*}f^\prime(x)\end{align*}$ . Before continuing with the lesson, try listing functions that are antiderivative and derivative pairs? 
  ::您在如何找到函数 f(x) 的衍生物、 f*(x) 和区分过程方面花费了许多经验教训。 这样一来,函数 f(x) 或函数的组合就会有一个名称, 当有区别时可以产生 f*(x) 或函数的组合: f(x) 和 f*(x) 是一对, f(x) 被称为 f*(x) 的抗衍生物。 在继续上课之前, 请尝试列出反衍生和衍生的对的函数 ?

  播放段落

  The Antiderivative
  ::抗异狄氏剂

  播放段落

  Let’s start off and introduce the idea of the antiderivative of a function.
  ::让我们从头开始, 提出功能的抗降解性理念。

  播放段落

  A function $\begin{align*}F(x)\end{align*}$ is called an  antiderivative of a function $\begin{align*}f\end{align*}$ if $\begin{align*}F^\prime(x) = f(x)\end{align*}$ for all  $\begin{align*}x\end{align*}$ in the domain of $\begin{align*}f\end{align*}$ .
  ::F(x) 函数在 f 域的所有 x 函数中被称为 f 的 F* (x) =f(x) 的反效果函数 f 。

  播放段落

  How is this definition used?
  ::这一定义是如何使用的?

  播放段落

  Consider the function $\begin{align*}f(x) = 3{x^2}.\end{align*}$
  ::考虑函数 f( x)=3x2。

  播放段落

  Can you think of a function $\begin{align*}F(x)\end{align*}$ such that $\begin{align*}F^\prime(x) = f(x)\end{align*}$ ? You should be able to think of lots of them.
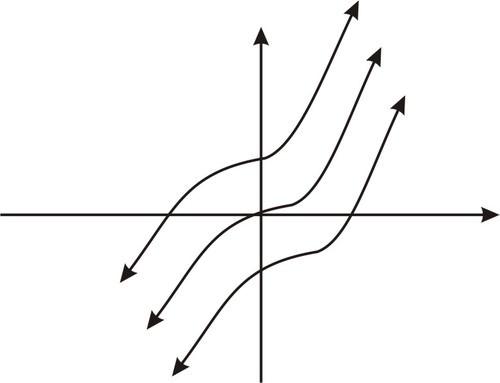
  ::您能想到F(x) 这样的函数吗? 您应该能够想到其中的很多函数 。

  播放段落

  Since we differentiate $\begin{align*}F(x)\end{align*}$ to get $\begin{align*}f(x)\end{align*}$ , we see that $\begin{align*}F(x) = {x^3} + C\end{align*}$ will work for any constant $\begin{align*}C\end{align*}$ . Graphically, we can think of the set of all antiderivatives as vertical transformations of the graph of $\begin{align*}F(x) = x^3\end{align*}$ . The figure shows two such transformations.
  ::由于我们将 F(x) 区分为 f(x),我们看到 F(x) =x3+C 将为任何常数 C. 工作。 从图形上看,我们可以将所有抗降解剂都视为F(x) =x3 图表的垂直转换。 图中显示了两种这样的转换。

  

  播放段落

  With our definition and initial example, we now look to formalize the definition and develop some useful rules for computational purposes, and begin to see some applications.
  ::以我们的定义和初步例子,我们现在期待正式确定定义,为计算目的制定一些有用的规则,并开始看到一些应用。

  播放段落

  Introduction to Indefinite Integrals
  ::无限期综合症介绍

  播放段落

  The process of finding antiderivatives is called antidifferentiation , more commonly referred to as integration . Here is how the integration is indicated and how it works:
  ::寻找抗降解剂的过程称为反差异,更常见地称为融合。

  播放段落

  $\begin{align*}F^\prime(x) =f(x) \end{align*}$ ... Start with the  differential equation that represents the definition of the antiderivative
  ::F`(x)=f(x)...以代表抗降解剂定义的不同方程开始

  播放段落

  $\begin{align*}\int F^\prime (x)dx =\int f(x) dx \end{align*}$ ... Invoke the integration (antidifferentiation) operation using the special symbol $\begin{align*}\int\end{align*}$ .
  ::*F*(x)dx**f(x)dxxxxxxxxxxxxxx...使用特殊符号** 启动整合(对应差异)操作。

  播放段落

  $\begin{align*}F(x)+C=\int f(x) dx \end{align*}$ ... Obtain the antiderivative  $\begin{align*}F(x)\end{align*}$ and a constant of integration , $\begin{align*}C\end{align*}$ .
  ::F(x)+Cf(x)dx.获得抗降解F(x)和恒定集成,C。

  播放段落

  $\begin{align*}\int f(x) dx=F(x)+C\end{align*}$ ... Note that if we differentiate both sides, we get back the original equation:
  ::\f(x)dx=F(x)+C.请注意,如果我们将两边区分开来,我们就会回到原来的方程:

  播放段落

  $$\begin{align*}\frac{d}{dx}\left[\int f(x)dx\right]=f(x)=\frac{d}{dx} \left[F(x)+C \right]=F^ \prime(x)\end{align*}$$
  ::ddx[\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  We refer to $\begin{align*}\int f (x)dx\end{align*}$ as “the indefinite integral of $\begin{align*}f(x)\end{align*}$ with respect to  $\begin{align*}x\end{align*}$ ”. The function $\begin{align*}f(x)\end{align*}$ is called the  integrand and the constant  $\begin{align*}C\end{align*}$ is called the constant of integration . Finally the symbol  $\begin{align*}dx\end{align*}$ indicates that we are to integrate with respect to $\begin{align*}x\end{align*}$ .
  ::我们将f(x)dx称为“与x有关的f(x)的无限期组成部分”。函数f(x)称为整数,常数C称为常数集成。最后,符号dx表示我们将结合x。

  播放段落

  Using this notation, we would summarize the last example as follows:
  ::使用这个符号,我们将最后一个例子总结如下:

  播放段落

  $$\begin{align*}\int 3x^2 dx=x^3+C\end{align*}$$
  ::3x2dx=x3+C

  播放段落

  Now, consider the function $\begin{align*}f(x) = \cos x\end{align*}$
  ::现在, 考虑函数 f( x) =cosx

  播放段落

  Can you think of a function $\begin{align*}F(x)\end{align*}$ such that $\begin{align*}F^\prime(x) = f(x)\end{align*}$ ?
  ::您能想到 F( x) 的函数吗? F* (x) =f(x) ?

  播放段落

  If you said $\begin{align*}F(x) = \sin x + C\end{align*}$ you would be correct and here is how this would be written.
  ::如果你说F(x)=sinx+C,你会说对了,这是如何写成的。

  播放段落

  $\begin{align*}f(x)=F^\prime(x)\end{align*}$ . . . Start with the differential equation that represents the definition of the antiderivative
  ::f(x) = F}(x) = F}(x) . 。从代表抗降解剂定义的差别方程开始。

  播放段落

  $\begin{align*}\cos x=F^\prime(x)\end{align*}$ . . . Substitute for $\begin{align*}f(x)\end{align*}$
  ::COsx=F}(x) . f(x) 替代

  播放段落

  $\begin{align*}\int \cos x\ dx=\int F^\prime(x) dx\end{align*}$ . . . Invoke the integration (antidifferentiation) operation using the special symbol $\begin{align*}\int\end{align*}$ .
  ::*cosx dxF*(x)dx. 使用特殊符号启动整合(对应差异)操作 *{}。

  播放段落

  $\begin{align*}\int \cos x\ dx=F(x)+C\end{align*}$ . . . Obtain the antiderivative $\begin{align*}F(x)\end{align*}$  and a constant of integration, $\begin{align*}C\end{align*}$ .
  ::*cosx dx=F(x)+C.获得抗降解F(x)和恒定集成,C.

  播放段落

  $\begin{align*}\int\cos x\ dx=\sin x+C\end{align*}$ . . . We know $\begin{align*}F(x)=\sin x\end{align*}$  because if we differentiate both sides, we get back the original equation.
  ::*cosx dx=sinx+C.我们了解F(x)=sinx,因为如果我们将两边区分开来,我们就会回到原来的方程。

  播放段落

  We have looked at the of a number of functions through the calculus concepts and can put together a list of functions and their antiderivatives as shown below.
  ::我们通过微积分概念审视了若干功能,并可以列出一系列功能及其抗降解剂,如下文所示。

  Summary of Basic Indefinite Integrals And Antiderivatives

  播放段落 Function $\begin{align*}f(x)\end{align*}$ ::函数f(x)	播放段落 Antiderivative $\begin{align*}\int f(x)dx=F(x)+C\end{align*}$ ::抗性 f(x)dx=F(x)+C
  1	$\begin{align*}x+C\end{align*}$
  $\begin{align*}x\end{align*}$	播放段落 $\begin{align*}\frac{{{x^2}}}{2} + C\end{align*}$ ::x22+Cx22+C
  播放段落 $\begin{align*}{x^2}\end{align*}$ ::x2x2	播放段落 $$\begin{align*}\frac{{{x^3}}}{3} + C\end{align*}$$ ::x33+C x33+C
  播放段落 $\begin{align*}{x^n}{\rm{,}}\end{align*}$ ::xn, 播放段落 $\begin{align*}n \ne - 1\end{align*}$ ::n1	播放段落 $$\begin{align*}\frac{{{x^{n + 1}}}}{{n + 1}} + C\end{align*}$$ ::xn+1n+1+C
  播放段落 $\begin{align*}\frac{1}{x}\end{align*}$ ::1x 1x	播放段落 $\begin{align*}\ln x + C\end{align*}$ ::Inx+C 内载+C
  播放段落 $\begin{align*}\sin x\end{align*}$ ::异性	播放段落 $\begin{align*}- \cos x + C\end{align*}$ ::- COSx+C
  播放段落 $\begin{align*}\cos x\end{align*}$ ::COsx COsx	播放段落 $\begin{align*}\sin x+C\end{align*}$ ::罪恶+C
  播放段落 $\begin{align*}{\sec ^2}x\end{align*}$ ::秒2x	播放段落 $\begin{align*}\tan x + C\end{align*}$ ::henx+C 键
  播放段落 $\begin{align*}{\csc ^2}x\end{align*}$ ::csc2x csc2x	播放段落 $\begin{align*}- \cot x + C\end{align*}$ ::- 丙烷+C
  播放段落 $\begin{align*}\sec x\tan x\end{align*}$ ::ex当量	播放段落 $\begin{align*}\sec x + C\end{align*}$ ::秒+C
  播放段落 $\begin{align*}\csc x\cot x\end{align*}$ ::ccxcox 氧化物	播放段落 $\begin{align*}- \csc x + C\end{align*}$ ::- cscx+C
  播放段落 $\begin{align*}{e^x}\end{align*}$ ::以 un, un, un, un, un, un, un, un, un, un, un, un, un, un	播放段落 $\begin{align*}{e^x} + C\end{align*}$ ::Ex+C 后加 C
  播放段落 $\begin{align*}{b^x}\end{align*}$ ::bx bx 播放段落 $\begin{align*}b > 0\end{align*}$ ::b >0	播放段落 $\begin{align*}\frac{{{b^x}}}{{\ln b}} + C\end{align*}$ ::bxlnb+C
  播放段落 $\begin{align*}\frac{1}{{x\ln b}}\end{align*}$ ::1x一亿b	播放段落 $\begin{align*}{\log _b}x + C\end{align*}$ ::对数bx+C

  播放段落

  As with differentiation, there are several rules for dealing with the sum and difference of integrable functions. 
  ::与区别对待一样,在处理不可区分功能的总和和差异方面也有几项规则。

  播放段落

  Basic Integration Rules
  ::基本融合规则

  播放段落

  If  $\begin{align*}f\end{align*}$ and  $\begin{align*}g\end{align*}$ are integrable functions, and  $\begin{align*}C\end{align*}$ is a constant, then:
  ::如果f和g是不可磨灭的函数,而C是一个常数,那么:

  播放段落

  $$\begin{align*}\int[f(x)+g(x)]dx &=\int f(x)dx+\int g(x)dx, \\ \int[f(x)-g(x)]dx &=\int f(x)dx-\int g(x)dx, \\ \int[Cf(x)]dx &=C\int f(x)dx.\end{align*}$$
  ::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\(x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Compute the following indefinite integral.
  ::计算以下的无限整体。

  播放段落

  $$\begin{align*}\int \left[2x^3+\frac{3}{x^2}-\frac{1}{x}\right]dx.\end{align*}$$
  ::[2x3+3x2 -1x]dx。

  播放段落

  Using our rules we have
  ::使用我们的规则

  播放段落

  $$\begin{align*}\int\left[2x^3+\frac{3}{x^2}-\frac{1}{x}\right]dx &=2\int x^3dx+3\int\frac{1}{x^2}dx-\int\frac{1}{x}dx\\ &=2\left(\frac{x^4}{4}\right)+3\left(\frac{x^{-1}}{-1}\right)-\ln x+C\\ &=\frac{x^4}{2}-\frac{3}{x}-\ln x+C.\end{align*}$$
  ::[2x3+3x2-1x]dx=2x3dx+31x2dxx*1xxx=2(x44)+3(x-1-1-1)-(x+C=x42-3x-lnx+C。

  播放段落

  Note that sometimes our rules need to be modified slightly due to operations with constants.
  ::请注意,有时由于使用常数操作,我们的规则需要稍作修改。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to try listing functions that are antiderivative and derivative pairs. By doing so you are presenting the results of differentiation and integration operations. If all you did was to list the function being differentiated as the antiderivative, this is correct. By now you have realized that there is a family of antiderivatives you could have chosen from, each differing by a constant of integration.
  ::早些时候, 您被要求尝试列出具有抗降解和衍生作用的函数。 这样您就可以展示差异化和整合操作的结果。 如果您所做的全部只是列出被区别的函数作为抗降解作用, 这是正确的 。 您现在已经意识到, 您可以从中选择一个有抗降解作用的家族, 每个家族都因不断的整合而不同 。

  播放段落

  Example 2
  ::例2

  播放段落

  Compute the following indefinite integral:
  ::计算以下不定期整体部分:

  播放段落

  $$\begin{align*}\int e^{3x}dx.\end{align*}$$
  ::e3xxxxx. \fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F2F}[注: e3xxxxxxx]

  播放段落

  We first note that our rule for integrating exponential functions does not work here since $\begin{align*}\frac{d}{dx}e^{3x}=3e^{3x}\end{align*}$ . However, if we remember to divide the original function by the constant then we get the correct antiderivative and have
  ::我们首先注意到,我们整合指数函数的规则在这里行不通,因为 ddxexe3x=3e3x。然而,如果我们记得将原有函数除以常数,那么我们就会得到正确的抗衍生功能,并

  播放段落

  $$\begin{align*}\int e^{3x}dx=\frac{e^{3x}}{3}+C.\end{align*}$$
  ::e3xxx=e3x3+C。

  播放段落

  We can now re-state the rule in a more general form as
  ::我们现在可以以更笼统的形式重述这一规则,因为:

  播放段落

  $$\begin{align*}\int e^{kx}dx=\frac{e^{kx}}{k}+C.\end{align*}$$
  ::-============================================================================================================================================================== ==========================================================================================================================================================方===================================================================================================================================================================================================

  播放段落

  Review
  ::回顾

  播放段落

  For #1-6, find an antiderivative of the function 
  ::# 1-6, 找到函数的抗变性

  播放段落
  1. $\begin{align*}f(x) = 1 - 3{x^2} - 6x\end{align*}$
     :xx) = 1 - 3x2 - 6x
  播放段落
  2. $\begin{align*}f(x) = x - {x^{\frac{2}{3}}}\end{align*}$
     :xx) =x-x23
  播放段落
  3. $\begin{align*}f(x) = \sqrt[5]{{2x + 1}}\end{align*}$
     ::f(x) = 52x+1
  播放段落
  4. $\begin{align*}f(x) = \cos x - x\end{align*}$
     :x) =cosx-x
  播放段落
  5. $\begin{align*}f(x) = {x^5} - 7{x^2} + 2\end{align*}$
     :x) =x5 - 7x2+2
  播放段落
  6. $\begin{align*}f(x) = {e^{ - 2x}} + {e^x}\end{align*}$
     :xx) =e-2x+ex

  播放段落

  For  #7-12, find the indefinite integral
  ::7 -12号,找到无期的完整体

  播放段落
  7. $\begin{align*}\int \left(2 + \sqrt 5 \right) dx\end{align*}$
     ::=============================================================================================================================== =========================================================================================
  播放段落
  8. $\begin{align*}\int 2 {(x - 3)^3}dx\end{align*}$
     :x-3)3dx
  播放段落
  9. $\begin{align*}\int \left(x^2 \cdot \sqrt[3]{x}\right) dx\end{align*}$
     :x23xx) dx
  播放段落
  10. $\begin{align*}\int {\left( {x + \frac{1}{{{x^4}\sqrt x }}} \right)} dx\end{align*}$
      ::*(x+1x4xx)dx
  播放段落
  11. $\begin{align*}\int {(\cos x + 2\sin x)dx}\end{align*}$
      :cosx+2sinx) dx
  播放段落
  12. $\begin{align*}\int {2\sin x\cos xdx}\end{align*}$
      ::2sinxxxxxxxx 2sinxxxxxxxxx
  播放段落
  13. Solve the differential equation $\begin{align*}f^\prime(x) = 4{x^3} - 3{x^2} + x - 3\end{align*}$ .
      ::解析差别方程 f_( x) = 4x3- 3x2+x-3 。
  播放段落
  14. Find the antiderivative $\begin{align*}F(x)\end{align*}$ of the function $\begin{align*}f(x) = 2{e^{2x}} + x - 2\end{align*}$ that satisfies $\begin{align*}F(0) = 5\end{align*}$ .
      ::查找函数 f( x) = 2e2x+x-2 的抗降解 F(x) F(x) , 满足 F( 0) = 5 。
  播放段落
  15. Evaluate the indefinite integral $\begin{align*}\int | x|dx\end{align*}$ (Hint: Examine the graph of $\begin{align*}f(x) = |x|\end{align*}$ .)
      ::评估不定期整体 xdx (提示: 检查 f( x) x x ) 的图表 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。