6.3 革命的固体:磁盘的体积

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 革命的固体:磁盘的体积

  Collapse Expand

  革命的固体:磁盘的体积

  播放段落

  You know  the volume of a solid can be  determined by knowing how the cross-sectional area in a plane perpendicular to the length (or height) varies over the height. In this concept, the cross-section considered will be a circle , because the solid will be a solid of revolution . Do you think that the method of computing the volume of a solid of revolution using circular cross-sections would be significantly different than the cross-section (slicing) method of the previous concept?
  ::您知道固体的体积可以通过知道一个与长度(或高度)相垂直的平面的横截面面积在高度(或高度)上如何变化来决定。 在这个概念中,考虑的横截面将是一个圆形,因为固体是革命的固态。 您是否认为使用圆截面计算革命固体体积的方法会与前一个概念的横截面(切除)方法大不相同?

  播放段落

  Volumes by Disks
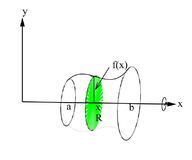
  ::磁盘的音量

  播放段落

  Suppose a function  $\begin{align*}f\end{align*}$ is continuous and non-negative on the interval  $\begin{align*}[a,b]\end{align*}$ , and suppose that  $\begin{align*}R\end{align*}$ is the region between the curve  $\begin{align*}f\end{align*}$ and the $\begin{align*}x\end{align*}$ -axis. If this region is revolved about the $\begin{align*}x\end{align*}$ -axis, it will generate a solid that will have circular cross-sections with radii of  $\begin{align*}f(x)\end{align*}$  at each  $\begin{align*}x\end{align*}$ . Each cross-sectional area can be calculated by $\begin{align*}A(x)=\pi[f(x)]^2\end{align*}$ .
  ::假设一个函数 f 在间隔[a,b] 上是连续的和非负的, 并假设 R 是曲线 f 和 x 轴之间的区域。 如果这个区域围绕 x 轴旋转, 它将产生一个固体, 其圆形交叉部分与 f (x) 的 f (x) 相交。 每个横切区域都可以由 A (x)\\\\ [f (x2) 计算 。

  

  

  
  

  播放段落

  Since the volume is defined as $\begin{align*}V=\int\limits_a^b A(x)dx\end{align*}$ , the volume of the solid is $\begin{align*}V=\int\limits_a^b \pi[f(x)]^2 dx\end{align*}$ .
  ::由于体积的定义是V=baa(x)dx,固体的体积是V=ba}[f(x)]2dx。

  播放段落

  Calculate the volume of the solid that is obtained when the region under the curve  $\begin{align*}\sqrt{x}\end{align*}$  is revolved about the  $\begin{align*}x\end{align*}$ -axis over the interval [1, 7].
  ::计算每秒[1, 7] 间距内 x轴围绕 X 轴旋转时获得的固体体积。

  播放段落

  As the figures below show,  the volume is
  ::如下图所示,数量如下图所示:

  播放段落

  $$\begin{align*}V &=\int\limits_a^b \pi[f(x)]^2 dx \\ &=\int\limits_1^7 \pi[\sqrt{x}]^2 dx \\ &=\pi \left[\frac{x^2}{2} \right]_1^7 \\ &=24 \pi. \end{align*}$$
  ::V=ba[f(x)]2dx=71[x]2dx[x22]71=24。

  

  
  

  

  
  

  播放段落

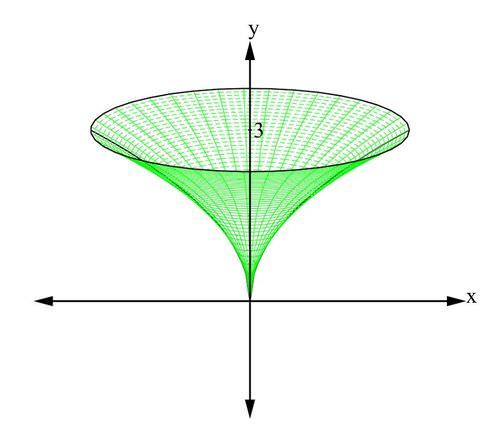
  Now, let's derive a formula for the volume of the sphere with radius $\begin{align*}r\end{align*}$ .
  ::现在,让我们用半径 r 得出一个球体体积的公式。

  播放段落

  One way to find the formula is to use the disk method . From your algebra, a circle of radius  $\begin{align*}r\end{align*}$  and center at the origin is given by the formula
  ::找到公式的一个方法就是使用磁盘方法。从您的代数中,公式给出了圆半径 r 和 源的中心

  播放段落

  $$\begin{align*}x^2+y^2=r^2\end{align*}$$
  ::x2+y2=r2

  播放段落

  If we revolve the circle about the $\begin{align*}x\end{align*}$ -axis, we will get a sphere. Using the disk method, we will obtain a formula for the volume. From the equation of the circle above, we solve for $\begin{align*}y\end{align*}$ :
  ::如果我们在 X 轴周围旋转圆圈, 我们就会得到一个球体。 使用磁盘方法, 我们将获得音量的公式 。 从上面圆形的方程式中, 我们为 y 解决 :

  播放段落

  $$\begin{align*}f(x)=y=\sqrt{r^2-x^2},\end{align*}$$
  :xx) =yr2-x2,

  播放段落

  thus
  ::因此,

  播放段落

  $$\begin{align*}V &=\int\limits_a^b \pi[f(x)]^2 dx \\ &=\int\limits_{-r}^{+r} \pi \left[\sqrt{r^2-x^2} \right]^2 dx \\ &=\pi \left[r^2x- \frac{x^3}{3} \right]_{-r}^r \\ &=\frac{4}{3} \pi r^3.\end{align*}$$
  ::V=ba[f(x)]2dxrr}[r2-x2]2]2dx[r2x-x33]r-r=43r3]。

  播放段落

  This is the standard formula for the volume of the sphere.
  ::这是球体体积的标准公式 。

  播放段落

  So far we have shown examples where the volume of the solid is determined by integrating the volume of disks, $\begin{align*}\pi [f(x)]^2 dx\end{align*}$ , generated by rotating about the $\begin{align*}x\end{align*}$ -axis. At times, the volume can be better determined by integrating along the $\begin{align*}y\end{align*}$ -axis using the following
  ::到目前为止,我们已展示了一些实例,说明固体的体积是用X轴旋转产生的磁盘量( {[f(x)]]2dx) 的集成量来决定的。有时,用下列方法结合Y轴就可以更好地确定体积:

  播放段落

  %5D%5E2%20dy.">

  $$\begin{align*}V=\int\limits_c^d \pi[f(y)]^2 dy.\end{align*}$$
  ::V=dc[f]2dy。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked whether the method of computing the volume of a solid of revolution using circular cross-sections would be significantly different than the cross-section (slicing) method of the previous concept. If you said that the methods should not be different, you were correct. The disk method discussed in this concept is just an application of the method of slicing discussed in the previous concept. The shape of the slice is a disk, so we use the formula for the area of a circle to find the volume of the disk.
  ::早些时候,有人问您,使用圆形横截面来计算革命固体体积的方法是否与前一个概念的横截面(切片)方法大不相同。 如果您说方法不应该不同, 您是对的。 此概念中讨论的磁盘方法只是应用前一个概念中讨论的切片方法。 切片的形状是一张磁盘, 所以我们使用圆圈区域的公式来查找磁盘的体积 。

  播放段落

  Example 2
  ::例2

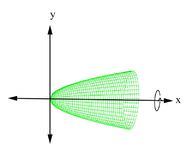
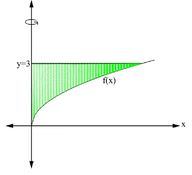
  播放段落

  What is the volume of the solid generated when the region enclosed by  $\begin{align*}y=\sqrt{x}\end{align*}$ , $\begin{align*}y=3\end{align*}$ , and  $\begin{align*}x=0\end{align*}$  is revolved about the $\begin{align*}y\end{align*}$ -axis?
  ::当以yx、y=3和 x=0 围绕 Y 轴旋转的区域时, 固体生成的量是多少 ?

  播放段落

  Since the solid generated is revolved about the $\begin{align*}y\end{align*}$ -axis (Figure 12), we must rewrite  $\begin{align*}y=\sqrt{x}\end{align*}$  as $\begin{align*}x=y^2\end{align*}$ .
  ::由于产生的固体围绕 Y 轴(图12)旋转,我们必须将 y x 重写为 x=y2 。

  播放段落

  Thus %3Dy%5E2"> $\begin{align*}u(y)=y^2\end{align*}$ .The volume is
  ::因此,u=y2. 体积是

  播放段落

  %5D%5E2%20dy%20%5C%5C%0A%26%3D%5Cint%5Climits_0%5E3%20%5Cpi%5By%5E2%5D%5E2%20dy%20%5C%5C%0A%26%3D%5Cint%5Climits_0%5E3%20%5Cpi%20y%5E4%20dx%20%5C%5C%0A%26%3D%5Cpi%20%5Cleft%5B%5Cfrac%7By%5E5%7D%7B5%7D%20%5Cright%5D_0%5E3%20%5C%5C%0A%26%3D%5Cpi%20%5Cleft%5B%5Cfrac%7B3%5E5%7D%7B5%7D-0%20%5Cright%5D%20%5C%5C%0A%26%3D%5Cfrac%7B243%20%5Cpi%7D%7B5%7D.">

  $$\begin{align*}V &=\int\limits_c^d \pi[u(y)]^2 dy \\ &=\int\limits_0^3 \pi[y^2]^2 dy \\ &=\int\limits_0^3 \pi y^4 dx \\ &=\pi \left[\frac{y^5}{5} \right]_0^3 \\ &=\pi \left[\frac{3^5}{5}-0 \right] \\ &=\frac{243 \pi}{5}.\end{align*}$$
  ::V=dc[u]2dy=30[y2]2uddy=30y4dx[y55]30[355-0]=243}5。

  

  
  

  

  播放段落

  Example 3
  ::例3

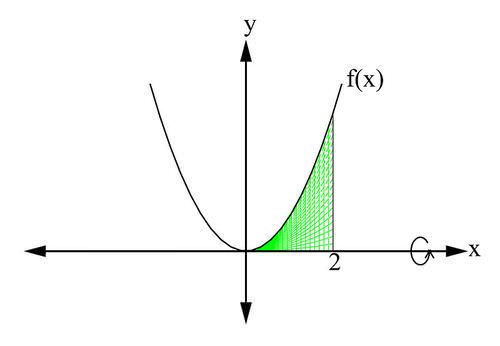
  播放段落

  A solid figure is created by rotating the region  $\begin{align*}R\end{align*}$  around the $\begin{align*}x\end{align*}$ -axis.  $\begin{align*}R\end{align*}$  is bounded by the curve  $\begin{align*}y=x^2\end{align*}$  and the lines $\begin{align*}x=0\end{align*}$  and $\begin{align*}x=2\end{align*}$ . Use the disc method to compute the volume of the solid.
  ::将 R 区域旋转到 x 轴周围,从而生成一个固态数字。 R 受曲线 y=x2 和 行 x=0 和 行 x =2 的约束,使用光碟法计算固体的体积。

  

  播放段落

  From the figure we can identify the limits of integration :  $\begin{align*}x\end{align*}$ runs from 0 to 4. Thus the volume of the solid will be
  ::从数字中我们可以确定集成的极限:x从0到4运行。 因此,固体的体积将是

  $\begin{align*}V\end{align*}$	$\begin{align*}=\int\limits_{a}^{b} \pi[f(x)]^2 dx\end{align*}$
  	$\begin{align*}=\int\limits_{0}^{2} \pi[x^2]^2 dx\end{align*}$
  	$\begin{align*}=\pi \left[\frac{x^5}{5} \right]_0^2\end{align*}$
  $\begin{align*}V\end{align*}$	$\begin{align*}=\frac{32}{5} \pi\end{align*}$

  播放段落

  Review
  ::回顾

  播放段落

  For  #1-4, find the volume of the solid generated by revolving the region bounded by the curves about the $\begin{align*}x\end{align*}$ -axis.
  ::在 # 1-4 中, 找到通过旋转生成的固体体积, 以 X 轴的曲线为界的区域为界 。

  播放段落
  1. $\begin{align*}y=\sqrt{9-x^2}\end{align*}$ , $\begin{align*}y=0\end{align*}$
     ::y9 - x2, y=0
  播放段落
  2. $\begin{align*}y=3+x\end{align*}$ , $\begin{align*}y=1+x^2\end{align*}$
     ::y=3+x,y=1+x2 y=3+x,y=1+x2
  播放段落
  3. $\begin{align*}y=sec \ x\end{align*}$ , $\begin{align*}y=\sqrt{2}\end{align*}$ , $\begin{align*}\frac{-\pi}{4} \le x \le \frac{\pi}{4}\end{align*}$
     ::y=sec x, y2, 4x4
  播放段落
  4. $\begin{align*}y=1\end{align*}$ , $\begin{align*}y=x\end{align*}$ , $\begin{align*}x=0\end{align*}$
     ::y=1, y=x, x=0 y=1, y=x, x=0

  播放段落

  For  #5-9, find the volume of the solid generated by revolving the region bounded by the curves about the $\begin{align*}y\end{align*}$ -axis.
  ::对于5-9, 找到圆圈生成的固体体积, 以Y轴曲线为界的区域为界 。

  播放段落
  5. $\begin{align*}y=x^3\end{align*}$ , $\begin{align*}x=0\end{align*}$ , $\begin{align*}y=1\end{align*}$
     ::y=x3, x=0, y=1 y=1
  播放段落
  6. $\begin{align*}x=y^2\end{align*}$ , $\begin{align*}y=x-2\end{align*}$
     ::x=y2, y=x- 2
  播放段落
  7. $\begin{align*}x=\csc \ y\end{align*}$ , $\begin{align*}y= \frac{\pi}{4}\end{align*}$ , $\begin{align*}y=\frac{3 \pi}{4}\end{align*}$ , $\begin{align*}x=0\end{align*}$
     ::x=csc y, y4, y= 34, x=0
  播放段落
  8. $\begin{align*}y=0\end{align*}$ , $\begin{align*}y=\sqrt{x}\end{align*}$ , $\begin{align*}x=4\end{align*}$
     ::y=0,yx, x=4
  播放段落
  9. $\begin{align*}x=\sqrt{16-y^2}\end{align*}$ , $\begin{align*}y=0\end{align*}$ , $\begin{align*}x=0\end{align*}$
     ::x16-y2, y=0, x=0
  播放段落
  10. The solid obtained by revolving about the $\begin{align*}x\end{align*}$ -axis the region between the $\begin{align*}x\end{align*}$ -axis and $\begin{align*}y=x^3\end{align*}$  for $\begin{align*}0 \le x \le 2\end{align*}$ .
      ::以 X 轴和 y=x 3 之间的区域为 X 轴旋转获得的 0.x xx = 2 的 固体 。
  播放段落
  11. The solid obtained by revolving about the $\begin{align*}x\end{align*}$ -axis the region between the $\begin{align*}x\end{align*}$ -axis and $\begin{align*}y=\sec \ x\end{align*}$  for $\begin{align*}-\frac{\pi}{4} \le x \le \frac{\pi}{4}\end{align*}$ .
      ::x轴与y=sec x之间的区域之间的 x轴旋转获得的固态, 以 4x4为单位 。
  播放段落
  12. The solid obtained by revolving about the $\begin{align*}x\end{align*}$ -axis the region between the $\begin{align*}x\end{align*}$ -axis and $\begin{align*}y=e^{-x}\end{align*}$  for $\begin{align*}0 \le x \le 1\end{align*}$ .
      ::通过旋转获得的关于x轴的固体, X轴与 y=e-x之间的区域为 0xxx1 。
  播放段落
  13. Find the volume of the solid generated by rotating the curve  $\begin{align*}y=3x+2\end{align*}$ about the $\begin{align*}x\end{align*}$ -axis on the interval $\begin{align*}0 \le x \le 4\end{align*}$ .
      ::查找通过旋转曲线 y=3x+2 生成的关于间距 0 ×x 4 的 x 轴的固体体积。
  播放段落
  14. Find the volume of the solid generated by rotating the area between the curves  $\begin{align*}y=0,y=3\end{align*}$ and  $\begin{align*}y=x\end{align*}$ about the $\begin{align*}y\end{align*}$ -axis.
      ::在 y 轴 的 y = 0. y = 3 和 y =x 之间旋转区域,以查找所生成的固体的体积。
  播放段落
  15. Find the volume of the solid generated by rotating about the $\begin{align*}x\end{align*}$ -axis the area between the curve  $\begin{align*}y=-2x^2+12x-10\end{align*}$ and the $\begin{align*}x\end{align*}$ -axis.
      ::查找在 x 轴上旋转产生的固体的体积,该轴是曲线 y2x2+12x-10 和 x 轴之间的区域。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。