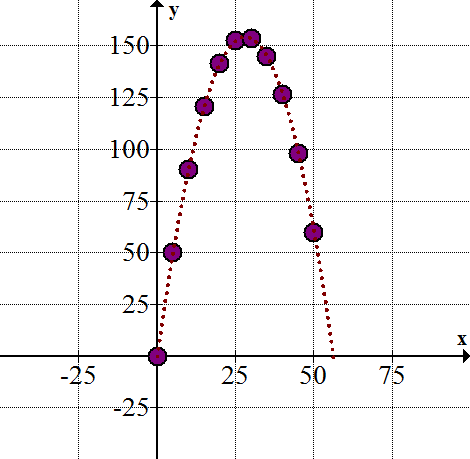Course: 10.1 参数赤道和平板曲线

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

参数等量和平面曲线

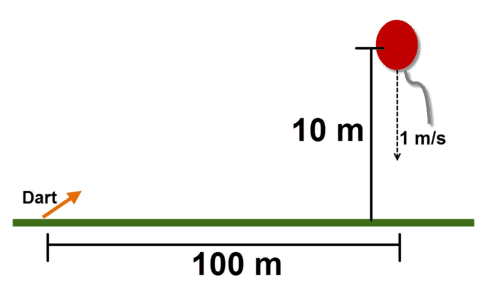
You’ve just joined your school’s physics team. For this year’s competition, you need to build a device that will fire a dart and pop a moving balloon. The balloon will slowly drop from a height of 10 meters at a rate of 1 m/s. Your device must aim accurately from 100 meters away. If the horizontal speed of your dart is 50 m/s, what must its vertical speed be in order for it to pop the balloon? To solve this problem, you’ll need to model the movement of the dart and the balloon in space, and make sure that the two paths cross at a single time.
::您刚刚加入学校的物理团队。今年的竞赛中,您需要建立一个能够发射飞镖并弹出移动气球的装置。气球将从10米高的高度以每秒1米的速度缓慢下降。您的装置必须从100米以外精确瞄准。如果您的飞镖水平速度是50米/秒, 弹出气球的垂直速度必须是什么? 要解决这个问题, 您需要模拟飞镖和气球在空间的移动, 确保两条路径同时交叉。

Introduction to Parametric Equations
::参数等量入门

A parametric equatio n gives the equation for a curve on the coordinate plane. It usually takes the form of $\begin{aligned} F (t) = (x (t), y (t)) \end{aligned}$ where the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ coordinates are given by two different functions of the variable $\begin{aligned} t \end{aligned}$ . Scientists and engineers find parametric equations most useful for analyzing variables that change over time, such as position in space, or how two populations relate to each other.
::参数方程给出坐标平面上曲线的方程。它通常采取F(t)=(x(t),y(t))的形式, x和y坐标由变量 t的两个不同的函数给定。科学家和工程师发现参数方程对于分析随时间变化的变量(如空间位置)或两个组群如何相互关联最为有用。

When an object moves on a plane, you can write one equation to describe its horizontal movement over time and one equation to describe its vertical movement over time. The parametric equation then describes the object’s position on the plane over time.
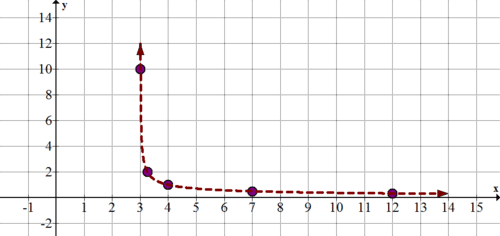
::当一个物体在平面上移动时,您可以写一个方程式来描述其随时间而水平移动的情况,一个方程式来描述其随时间而垂直移动的情况。然后,参数方程式来描述该物体随时间在平面上的位置。

You can use a table to help plot a parametric equation. Suppose that $\begin{aligned} x (t) = t^{2} + 3 \end{aligned}$ , and $\begin{aligned} y (t) = \frac{1}{t} \end{aligned}$ . The following table shows the values of $\begin{aligned} x (t) \end{aligned}$ and $\begin{aligned} y (t) \end{aligned}$ for various values of $\begin{aligned} t \end{aligned}$ .
::您可以使用一个表格来帮助绘制参数方程式。假设 x( t) = t2+3 和 y( t) = 1t。下表显示 t 各种值的 x( t) 和 y( t) 值。

$\begin{aligned} t \end{aligned}$	$\begin{aligned} x (t) \end{aligned}$	$\begin{aligned} y (t) \end{aligned}$
0	3	n/a
.1	3.01	10
.5	3.25	2
1	4	1
2	7	.5
3	12	.3333

The graph of the function would include an asymptote at $\begin{aligned} x = 3 \end{aligned}$ , and the set of points defined by $\begin{aligned} (x (t), y (t)) \end{aligned}$ .
::函数图中将包括 x=3 的星点和由 (x(t),y(t)) 定义的一组点。

An object whose movement was governed by $\begin{aligned} x (t) \end{aligned}$ and $\begin{aligned} y (t) \end{aligned}$ would be at (4, 1) when $\begin{aligned} t = 1 \end{aligned}$ , at (7, .5) when $\begin{aligned} t = 2 \end{aligned}$ and at (12, .3333) when $\begin{aligned} t = 3 \end{aligned}$ . The parametric function gives you extra information that isn’t obvious from the graph. It doesn’t just tell you where an object will be, but also when it will get there.
::由 x(t) 和 y(t) 调节其运动的物体在 t=1 时( 4, 1) , t=2 时( 7, 5) , t=2 时( 12, 3333 ) , t=3 时( 12, 3333) , 该参数函数为您提供了从图中看不出来的额外信息。它不仅告诉您一个对象会在哪里, 还会在何时到达那里。

Consider the following parametric equation.
::考虑以下参数方程。

\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 5 t \\ y (t) & = 55 t - \frac{1}{2} (9.8) t^{2} \end{aligned}

::F(t)=(x(t),y(t))x(t)=5ty(t)=55t-12(9.8)t2

Let's create a table showing values from $\begin{aligned} t = 0 \end{aligned}$ to $\begin{aligned} t = 10 \end{aligned}$ . Then, graph $\begin{aligned} F (t) \end{aligned}$ .
::让我们创建一个表格,显示从 t=0 到 t=10 的数值。然后,图F(t) 。

First, create a table and substitute in values for $\begin{aligned} t, x (t) \end{aligned}$ and $\begin{aligned} y (t) \end{aligned}$ .
::首先,为 t、x(t) 和 y(t) 创建一个表格,并替换 t、x(t) 和 y(t) 的值。

$\begin{aligned} t \end{aligned}$	$\begin{aligned} x (t) \end{aligned}$	$\begin{aligned} y (t) \end{aligned}$
0	0	0
1	5	50.1
2	10	90.4
3	15	120.9
4	20	141.6
5	25	152.5
6	30	153.6
7	35	144.9
8	40	126.4
9	45	98.1
10	50	60.0

Then, use these points to graph the curve.
::然后,用这些点来绘制曲线图。

You may notice that this curve models the motion of a projectile fired from a cannon with an initial horizontal velocity of 5 m/s and an initial vertical velocity of 55 m/s. Using parametric equations let you see the position of the projectile at each time, $\begin{aligned} t \end{aligned}$ , during its flight. When $\begin{aligned} y (t) = 0 \end{aligned}$ , the object has hit the ground.
::您可能注意到, 此曲线模拟从最初水平速度为5米/ 秒、最初垂直速度为55米/ 秒的炮火中发射的弹体的运动。使用参数方程式, 使您在飞行中每次看到弹体的位置, t。当 y( t) =0 时, 物体撞击了地面。

You can convert parametric equations to an equation that only uses the variables $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . This conversion will give you an equation for the curve, but will not let you find out where an object is at a specific time.
::您可以将参数方程转换为只使用变量 x 和 y 的方程。此方程转换将为曲线提供一个方程, 但不会让您在特定时间找到对象的位置。

Let's convert the following equation into a single equation in $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::让我们将以下方程式转换成 x 和 y 中的单方程式。

\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 5 t \\ y (t) & = 55 t - \frac{1}{2} (9.8) t^{2} \end{aligned}

To begin, solve

\begin{aligned} x (t) = 5 t \end{aligned}

for

\begin{aligned} t \end{aligned}

\begin{aligned} \frac{x (t)}{5} = t \end{aligned}

::F( t) = (x( t) y( t) x( t) x( t) x( t) x( t) 5ty( t) = 55t- 12( 9. 8) t2 开始, 解x( t) = 5t t: x( t) 5=t

Now, substitute for $\begin{aligned} t \end{aligned}$ in the equation $\begin{aligned} y (t) \end{aligned}$ :
::现在,在 y( t) 等式中, t 取代 t :

\begin{aligned} y (t) & = 55 t - \frac{1}{2} (9.8) t^{2} \\ y (t) & = 55 (\frac{x (t)}{5}) - \frac{1}{2} (9.8 {(\frac{x (t)}{5})}^{2}) \end{aligned}

::y(t)=55t-12(9.8)t2y(t)=55(x(t)5)-12(9.8(x)(t)5)2

Simplify:
::简化 :

$\begin{aligned} y (t) = 11 x (t) - \frac{9.8}{50} (x^{2} (t)) \end{aligned}$
::y(t)=11x(t)-9.850(x2(t))

The parabola $\begin{aligned} y = 11 x - \frac{9.8}{50} x^{2} \end{aligned}$ describes the path of the object in the parametric equation $\begin{aligned} F (t) \end{aligned}$ .
::抛物线y=11x-9.850x2 表示参数方程式F(t)中对象的路径。

To find the solution for a system of parametric equations, you have to determine if the paths cross and if both objects will be in the same place at the same time.
::要找到参数方程系统的解决方案, 您必须确定路径是否交叉, 以及两个对象是否同时在同一位置。

A projectile has been fired from a cannon. Its path can be described by the parametric equation:
::炮弹是从大炮上发射的,其路径可以用参数方程式来描述:

\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 5 t \\ y (t) & = 55 t - \frac{1}{2} (9.8) t^{2} \end{aligned}

::F(t)=(x(t),y(t))x(t)=5ty(t)=55t-12(9.8)t2

A second projectile is fired from another cannon. Its path can be described as the parametric equation:
::第二枚炮弹是从另一大炮中发射的,其路径可称为参数等式:

\begin{aligned} G (t) & = (x_{2} (t), y_{2} (t)) \\ x_{2} (t) & = 50 - 10 t \\ y_{2} (t) & = 75 t - \frac{1}{2} (9.8) t^{2} \end{aligned}

::G(t) = (x2(t) ,y2(t) ) x2(t) = 50- 10ty2(t) = 75t- 12(9.8) t2

Do the paths of the projectiles cross? Will the projectiles collide at any time $\begin{aligned} t \end{aligned}$ ?
::射弹的路径交叉吗?

To solve this problem, you’ll need to put both $\begin{aligned} F (t) \end{aligned}$ and $\begin{aligned} G (t) \end{aligned}$ in terms of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . Earlier, you found that $\begin{aligned} F (t) \end{aligned}$ can be rewritten as $\begin{aligned} y = 11 x - \frac{9.8}{50} x^{2} \end{aligned}$ or $\begin{aligned} y = 11 x - .196 x^{2} \end{aligned}$ . Now you need to put $\begin{aligned} G (t) \end{aligned}$ in terms of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::要解决这个问题, 您需要将 F( t) 和 G( t) 都放在 x 和 y 上。早些时候, 您发现 F( t) 可以重写为 y= 11x- 9. 850x2 或 y= 11x-. 196x2. 现在您需要将 G( t) 放在 x 和 y 上。

Solving $\begin{aligned} x_{2} (t) \end{aligned}$ for $\begin{aligned} t \end{aligned}$ yields $\begin{aligned} \frac{x - 50}{- 10} = t \end{aligned}$ .
::t 产量 x- 50- 10= t 的溶剂x2( t) 。

After you substitute this value for $\begin{aligned} t \end{aligned}$ into $\begin{aligned} y_{2} (t) \end{aligned}$ , you’ll see that $\begin{aligned} y = - .049 x^{2} - 2.6 x + 252.5 \end{aligned}$ .
::在将 t 替换为y2( t) 后, 你会看到 y. 049x2 - 2. 6x+252.5 。

To find the $\begin{aligned} x \end{aligned}$ value for where the two objects cross, set the two equations that have been solved for $\begin{aligned} y \end{aligned}$ equal to each other, then simplify.
::要找到两个对象交叉位置的 x 值, 请设定y 等量的y 解答的两方程式, 然后简化。

\begin{aligned} 11 x - .196 x^{2} & = - .049 x^{2} - 2.6 x + 252.5 \\ 0 & = .147 x^{2} - 13.6 x + 252.5 \end{aligned}

::11 - 196x2 . 049x2 - 2.6x+252.50=.147x2 - 13.6x+252.5

Solve the quadratic equation for $\begin{aligned} x \end{aligned}$ and you will find $\begin{aligned} x = 25.7119 \end{aligned}$ or $\begin{aligned} x = 66.8051 \end{aligned}$ . Now, substitute these values for $\begin{aligned} x \end{aligned}$ back into the original equations that were solved for $\begin{aligned} y \end{aligned}$ to find the corresponding $\begin{aligned} y \end{aligned}$ -coordinates. This will give you the points where the paths of the projectiles cross.
::解析 x 的二次方程式, 您将会找到 x=25.7119 或 x= 66. 8051。现在, 将这些数值替换为 x 返回原始方程式, 这些方程式已经解决了 y 以找到相应的 Y 坐标。这将为您提供射弹交叉路径的点。

The paths cross at (25.7119, 153.25) and (66.8051, -139.88). However, the second point is impossible in this context, since once a projectile reaches $\begin{aligned} y = 0 \end{aligned}$ , it has hit the ground and stopped moving.
::在25.7119、153.25和66.8051、139.88处的路径交叉点上,但第二点在此情况下是不可能的,因为一旦一个射弹到达y=0,它就击中地面并停止移动。

To see if the paths collide, you must see if both projectiles reach (25.7119, 153.25) at the same time.
::要看路径相撞时, 您必须同时看两枚射弹是否达到( 25.7119, 153. 25) 。

Start with $\begin{aligned} F (t) \end{aligned}$ where you know that $\begin{aligned} \frac{x_{1} (t)}{5} = t \end{aligned}$ .
::在您知道 x1(t)5=t 的地方, F(t) 开始。

Substitute 25.7119 (the $\begin{aligned} x \end{aligned}$ -coordinate of the potential collision) into this equation and you get $\begin{aligned} t = 5.14 \end{aligned}$ .
::以25.7119(潜在碰撞的X坐标)替代这个方程,你得到t=5.14。

Now consider $\begin{aligned} G (t) \end{aligned}$ where you know that $\begin{aligned} \frac{x_{2} (t) - 50}{- 10} = t \end{aligned}$ .
::现在在您知道 x2( t)- 50- 10=t 的地方考虑 G( t) 。

When you substitute 25.7119 into this equation, you’ll find that the second projectile reaches this point at $\begin{aligned} t = 2.43 \end{aligned}$ . Since the two projectiles reach this point at two different times, they do not actually collide.
::当您在此方程中替换25.7119时, 你会发现第二枚投射弹到达 t=2.43的这个点, 因为两枚射弹在两个不同的时间到达这个点, 它们实际上不会相撞。

Did you notice how both $\begin{aligned} y_{1} (t) \end{aligned}$ and $\begin{aligned} y_{2} (t) \end{aligned}$ contained the expression “ $\begin{aligned} - \frac{1}{2} 9.8 t^{2} \end{aligned}$ ”? This is because in the real world, when an object is dropped from rest, the change in its vertical position can be represented by $\begin{aligned} - \frac{1}{2} 9.8 t^{2} \end{aligned}$ . The 9.8 represents $\begin{aligned} 9.8 m / s^{2} \end{aligned}$ which is the acceleration due to gravity. For $\begin{aligned} y_{1} (t) \end{aligned}$ and $\begin{aligned} y_{2} (t) \end{aligned}$ , the first part of their expressions ( $\begin{aligned} 55 t \end{aligned}$ and $\begin{aligned} 75 t \end{aligned}$ ) represented the initial vertical velocities of the projectiles. The second part of their expressions $\begin{aligned} (- \frac{1}{2} 9.8 t^{2}) \end{aligned}$ represented the downwards movement due to gravity.
::您是否注意到 y1 (t) 和 y2 (t) 中是如何包含“ -129.8t2” 的? 这是因为在现实世界中,当一个物体从休息处掉落时,其垂直位置的变化可以代表-129.8t2。 9.8 表示9.8 m/s2, 即因重力而加速。对于 y1 (t) 和 y2(t) 来说,其表达式的第一部分(55t 和 75t) 表示射弹的初始垂直速度。其表达式的第二部分(-129.8t2) 表示因重力而向下移动。

Examples
::实例

Example 1
::例1

Earlier, you were asked to help your physics team create a mathematical model of a problem with a balloon that is 100 meters away. It’s dropping at a rate of 1 m/s from an initial height of 10 meters. Meanwhile, you can fire your dart from the ground with a horizontal velocity of 50 m/s. You need to calculate the initial vertical velocity of your dart, keeping in mind that gravity will affect its flight.
::早些时候, 您被要求帮助您的物理团队创建一个数学模型, 模拟气球在100米外的问题。气球从最初的10米高度以每秒1米的速度下降。与此同时, 您可以从地面发射飞镖, 水平速度为50米/秒。您需要计算飞镖的初始垂直速度, 同时铭记重力会影响它的飞行。

Parametric equations can turn this problem from a complicated one to a simple one.
::参数方程式可以把这个问题从一个复杂的问题变成一个简单的问题。

Start with two parametric equations. To express the position of the balloon over time you can use:
::以两个参数方程式开始。要显示气球在一段时间内的位置, 您可以使用 :

\begin{aligned} F (t) & = (x_{1} (t), y_{1} (t)) \\ x_{1} (t) & = 100 \\ y_{1} (t) & = 10 - t \end{aligned}

::F(t) = (x1(t),y1(t)) x1(t) = 100y1(t) =10-t

To express the position of the dart over time you can use:
::为了表达飞镖在一段时间内的位置,您可以使用:

\begin{aligned} G (t) & = (x_{2} (t), y_{2} (t)) \\ x_{2} (t) & = 50 t \\ y_{2} (t) & = v t - .5 (9.8) (t^{2}) \end{aligned}

::G(t) = (x2(t),y2(t)) x2(t) = 50ty2(t) = 50ty2(t) =vt- 5(9.8)(t2)

$\begin{aligned} x_{2} (t) \end{aligned}$ models the dart’s horizontal path, while $\begin{aligned} y_{2} (t) \end{aligned}$ models the vertical path of the dart and the effects of gravity on the dart’s flight. You’ll need to solve these equations in order to determine $\begin{aligned} v \end{aligned}$ , the upward velocity your dart needs to hit the target.
::x2(t) 模拟飞镖的水平路径,而 y2(t) 则模拟飞镖的垂直路径和重力对飞镖飞行的影响。您需要解决这些方程式,才能确定 , 您的飞镖的上行速度要击中目标。

You already know the $\begin{aligned} x \end{aligned}$ coordinate of the expected collision because the target is moving down a vertical line. The collision must happen at a point where $\begin{aligned} x = 100 \end{aligned}$ meters. Since $\begin{aligned} x_{2} (t) = 50 t \end{aligned}$ , the dart will have moved 100 meters along the horizontal axis when $\begin{aligned} t = 2 \end{aligned}$ . You can solve $\begin{aligned} y_{1} (t) \end{aligned}$ for $\begin{aligned} t = 2 \end{aligned}$ in order to find the height of the balloon after 2 seconds. You’ll find that, at $\begin{aligned} t = 2 \end{aligned}$ , the balloon is at (100, 8).
::您已经知道预期碰撞的 x 坐标, 因为目标正在向垂直线移动。碰撞必须在 x= 100 公尺处发生。从 x2( t) = 50t 开始, 飞镖将在 t= 2 时沿着水平轴移动100公尺。您可以在 t= 2 秒后解开 y1 (t) t= 2, 以找到气球的高度。您会发现, 在 t= 2 时, 气球在( 100, 8) 。

Now you must solve $\begin{aligned} y_{2} (t) \end{aligned}$ to find $\begin{aligned} v \end{aligned}$ , your initial vertical velocity. Substituting in the time and the height of the balloon gives you $\begin{aligned} 8 = v (2) - .5 (9.8) (2^{2}) \end{aligned}$ . Solve the equation for $\begin{aligned} v \end{aligned}$ , and you’ll find that your initial vertical velocity must be 13.8 m/s.
::现在您必须解决 y2( t) 才能找到 v, 您最初的垂直速度。以气球的时间和高度替代 8=v(2)- 5( 9.8)( 22) 。解决 v 的方程, 您就会发现您最初的垂直速度必须是13.8 m/ s 。

Using parametric equations turned a complicated problem into a system of equations solvable with basic algebra.
::使用参数方程式将复杂的问题变成一个用基本代数可溶解的方程式系统。

Example 2
::例2

Moira’s hobby involves leaping off of skyscrapers. (With proper safety equipment, of course.) She’s running at about 5 m/s when she jumps off “Trumpet Tower,” the corporate headquarters of a famous brass instrument maker. The tower is 250 meters tall. If the acceleration due to gravity is $\begin{aligned} - 9.8 m / s^{2} \end{aligned}$ , write a parametric equation to model her journey to the ground.
::莫伊拉的爱好是跳下摩天大楼。 (当然有适当的安全设备。 )当她从著名的铜制仪器制造商的公司总部“Trumpet Tower 塔”跳下时,她正以大约5米/秒的速度运行。该塔高250米。如果重力加速度为-9.8米/秒,则写一个参数方程式来模拟她的地面旅程。

Moira’s horizontal position can be described by her horizontal velocity times time. That is, $\begin{aligned} x (t) = 5 t \end{aligned}$ . Her vertical position can be described as her initial height, minus the height she loses as she falls. That is, $\begin{aligned} y (t) = 250 - \frac{1}{2} (9.8) t^{2} \end{aligned}$ . So, the equation to describe her motion is:
::Moira的水平位置可以用其水平速度时间来描述。也就是说, x( t) = 5t。她的垂直位置可以描述为她最初的高度, 减去她摔倒时失去的高度。也就是说, y( t) = 250 - 12( 9. 8) t2。因此, 描述她动作的方程式是 :

\begin{aligned} F (t) & = (x (t), y (t)) \\ x (t) & = 5 t \\ y (t) & = 250 - \frac{1}{2} (9.8) t^{2} \end{aligned}

::F(t) = (x(t) y(t) ) x(t) = 5ty(t) = 250- 12(9.8) t2

Example 3
::例3

Assuming the same information from Example 2, how long will it take Moira to hit ground, which is covered in proper safety equipment so that she’ll land safely?
::假设从例2得到的信息相同, 莫伊拉要多久才能到达地面? 地面由适当的安全设备覆盖,

To solve this problem, you’ll need to find the $\begin{aligned} t \end{aligned}$ for which $\begin{aligned} y (t) = 0 \end{aligned}$ . So,
::要解决这个问题,您需要找到y(t)=0的 t。所以,

\begin{aligned} y (t) & = 250 - \frac{1}{2} (9.8) t^{2} \\ 0 & = 250 - \frac{1}{2} (9.8) t^{2} \\ \frac{(250) (2)}{9.8} & = t^{2} \\ t & = 7.1429 \end{aligned}

::y( t) = 250- 12( 9.8) t20= 250-12( 9.8) t2( 250) (2)9. 8= t2t= 7. 1429

You only need to worry about the positive value for $\begin{aligned} t \end{aligned}$ , because time begins at 0 and a negative value would be meaningless in the context of this problem.
::你只需要担心t的正值, 因为时间从0开始, 而负值在这个问题上是毫无意义的。

Example 4
::例4

Assuming the same information from Example 2 and Example 3. Assume that the Trumpet Tower is perpendicular to the ground. How far from the base of the tower should Moira place her safety set-up so that the webcam footage of her jump is awesome instead of tragic?
::假设从例2和例3得到的信息相同,假设Trumpe Tower与地面是垂直的。莫伊拉应该将其安全装置设置在离塔底有多远的距离,以便她跳跃的摄像头片不是悲惨的,而是惊人的,而是惊人的?

In the previous example, you found out how long it took Moira to reach the ground. Evaluate $\begin{aligned} x (t) \end{aligned}$ at that time in order to find her horizontal position.
::在上一个例子中, 您发现莫伊拉到达地面花了多长时间。当时要评估 x (t) 才能找到横向位置。

\begin{aligned} x (t) & = 5 t \\ x & = 5 (2.2588) \\ x & = 11.294 \end{aligned}

t)=5tx=5(2.2588x=11.294)

Moira needs to place the gear she needs for a safe landing 11.294 meters away from the base of the building.
::莫伊拉需要把安全降落所需的装备放在离大楼基地11 294米的地方。

Review
::回顾

For #1-4, create a table for the given parametric equation showing values from $\begin{aligned} t = 0 \end{aligned}$ to $\begin{aligned} t = 6 \end{aligned}$ . Then, plot the points on a graph.
::对于 # 1-4, 为给定的参数方程创建一个表格, 显示从 t=0 到 t=6 的数值。然后, 在图表中绘制点数。

$\begin{aligned} F (t) & = (x (t), (y (t)) \\ x (t) & = t \\ y (t) & = t^{2} \end{aligned}$

::F(t) = (x(t) , (y(t) ) x(t) = t(t) = t2

$\begin{aligned} G (t) & = (x (t), (y (t)) \\ x (t) & = 3 t - 2 \\ y (t) & = t^{2} + 1 \end{aligned}$

::G( t) = (x( t) = (x( t) , (y( t) ) x( t) = 3t- 2y( t) = t2+1

$\begin{aligned} J (t) & = (x (t), (y (t)) \\ x (t) & = t + 1 \\ y (t) & = t^{2} \end{aligned}$

::J( t) = (x( t) , (y( t) ) x( t) = t+1y( t) = t2

$\begin{aligned} K (t) & = (x (t), (y (t)) \\ x (t) & = 7 t \\ y (t) & = 50 - \frac{1}{2} (9.8) t^{2} \end{aligned}$

:t)=(x(t),(y(t)))x(t)=7ty(t)=50-12(9.8)t2

For #5-8, convert the given parametric equation into a single equation in $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . Then, graph. Do your graphs match the points you plotted in #1-#4?
::对于# 5-8, 将给定的参数方程转换成 x 和 y 中的单方程。然后, 图形。您的图形是否匹配您在 # 1 - # 4 中绘制的点 ?

$\begin{aligned} F (t) & = (x (t), (y (t)) \\ x (t) & = t \\ y (t) & = t^{2} \end{aligned}$

::F(t) = (x(t) , (y(t) ) x(t) = t(t) = t2

$\begin{aligned} G (t) & = (x (t), (y (t)) \\ x (t) & = 3 t - 2 \\ y (t) & = t^{2} + 1 \end{aligned}$

::G( t) = (x( t) = (x( t) , (y( t) ) x( t) = 3t- 2y( t) = t2+1

$\begin{aligned} J (t) & = (x (t), (y (t)) \\ x (t) & = t + 1 \\ y (t) & = t^{2} \end{aligned}$

::J( t) = (x( t) , (y( t) ) x( t) = t+1y( t) = t2

$\begin{aligned} K (t) & = (x (t), (y (t)) \\ x (t) & = 7 t \\ y (t) & = 50 - \frac{1}{2} (9.8) t^{2} \end{aligned}$

:t)=(x(t),(y(t)))x(t)=7ty(t)=50-12(9.8)t2

For #9-11: A car drives off a cliff that is 25 meters high at 15 m/s. The acceleration due to gravity is $\begin{aligned} - 9.8 m / s^{2} \end{aligned}$ .
::#9-11:一辆汽车在15米/秒时从25米高的悬崖上驶离。重力加速度为-9.8米/秒。

Create a parametric equation to model the path of the car.
::创建参数方程以模拟汽车路径。

How long will it take for the car to reach the ground?
::车要多久才能到达地面?

If the cliff is perpendicular to the ground below it, how far from the base of the cliff will the car land?
::如果悬崖与下面的地面垂直, 车离悬崖底部有多远?

For #12-15: Your math teacher drops a water balloon off the top of the school which is 10 meters tall. The acceleration due to gravity on the water balloon is $\begin{aligned} - 9.8 m / s^{2} \end{aligned}$ . Your physics teacher sets up a dart 50 meters away with a horizontal velocity of $\begin{aligned} h \end{aligned}$ and a vertical velocity of 12 m/s.
::12-15:你的数学老师将水球从学校顶部扔下10米高的水球。水球重力加速度为-9.8米/秒。你的物理老师在50米外设置了飞镖,水平速度为h,垂直速度为12米/秒。

Create a parametric equation to model the path of the water balloon.
::创建参数方程以模拟水气球的路径。

Create a parametric equation to model the path of the dart (use $\begin{aligned} h \end{aligned}$ for the horizontal velocity).
::创建参数方程以模拟 dart 路径( 水平速度使用 h) 。

Find the value of $\begin{aligned} h \end{aligned}$ that your physics teacher should use to make sure the dart hits the water balloon.
::找出你的物理老师应该用来确保飞镖击中水气球的 h 值。

How far off the ground will the water balloon be when it is hit?
::水气球被击中时离地面有多远?

For #16-17: The paths of two projectiles are modeled by the parametric equations below.
::第16-17号:两个射弹的路径以下面的参数方程式为模型。

\begin{aligned} M (t) & = (x (t), (y (t)) \\ x (t) & = 10 t \\ y (t) & = 15 t - 0.5 (9.8) (t^{2}) \\ N (t) & = (x (t), (y (t)) \\ x (t) & = 12 t \\ y (t) & = 14 t - 0.5 (9.8) (t^{2}) \end{aligned}

t)=(x(t),(y(t)))x(t)=10ty(t)=15t-0.5(9.8)(t2)N(t)=(x(t),(y(t))x(t)=12ty(t)=14t=-0.5(9.8)(t2)

Once the projectiles have been launched, do their paths ever cross?
::一旦发射出射弹,他们的路径会交叉吗?

Will the projectiles ever actually collide because they are in the same place at the same time?
::这些射弹会因为同时在同一地点而实际相撞吗?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

参数等量和平面曲线

Introduction to Parametric Equations ::参数等量入门

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)