10.7 参数形式和微积分:曲线长度

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节参数表和计分表:曲线的长度

  折叠 展开

  参数表和计分表:曲线的长度

  播放段落

  On a test track at an auto factory, a driver puts two cars through their paces. He drives each car around the track at top speed, but the cars have different maximum speeds.  How can he compare their speeds and the distances that they travel during a thirty-minute test drive on the track?
  ::在汽车厂的测试轨迹上,驾驶员将两辆汽车放入他们的车速。他以最高速度驾驶每辆汽车,但汽车的最大速度不同。他如何比较车速和在赛道上30分钟的测试驱动器中车程的距离?

  播放段落

  Length of a Curve
  ::曲线长度

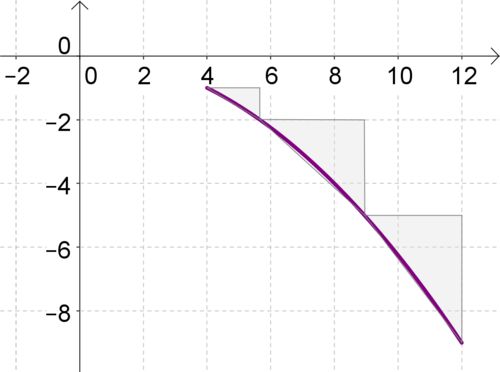
  播放段落

  Have you ever used the Pythagorean theorem to find the distance between two points on a line? On the coordinate plane, the linear distance formula is $\begin{array}{r}d=\sqrt{(x_1-x_0{)}^2+(y_1-y_0{)}^2}\end{array}$ .  The parametric formula for finding the distance along a curve is closely related to this formula.  Look at the curve below, for the function  $\begin{array}{r}F(t)=(x(t),y(t));x(t)=4t;y(t)=-t^2\end{array}$ between  $\begin{array}{r}t=1\end{array}$ and $\begin{array}{r}t=3\end{array}$ .
  ::您是否曾经使用 Pythagorean 定理来查找线上两点之间的距离? 在坐标平面上, 线性距离公式是 d=( x1- x0) 2+(y1-y0) 2。 查找曲线沿线距离的参数公式与此公式密切相关。 请看下面的曲线, 函数 F( t) =( x( t) ) =( y( t) ); x( t) =4t;y( t) =2 t=1 和 t=3 之间的曲线 。

  

  播放段落

  You could estimate the length of the curve by drawing right triangles, calculating the length of each hypotenuse, and adding all the lengths together. If you used very large triangles, your estimate would not be very accurate. But, as your triangles got smaller, your estimate would become more accurate. If you could make your triangles infinitely small, you’d be able to compute the exact measure of the curve.  In a way, the distance formula for lets you measure the curve with a continuous chain of infinitely small triangles.
  ::您可以通过绘制右侧三角形来估计曲线的长度, 计算每个下限的长度, 并将所有长度加在一起。 如果您使用非常大的三角形, 您的估算不会非常准确 。 但是, 随着三角形变小, 您的估算会变得更准确 。 如果您可以使三角形变得无限小, 您就可以计算曲线的精确度量。 在某种程度上, 允许您用一个由无限小三角形组成的连续链来测量曲线的距离公式 。

  播放段落

  The equation for the length of a curve in parametric form is: $\begin{array}{r}L=\underset{a}{\overset{b}{\int }}\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t){)}^2}dt\end{array}$ . Remember, a derivative tells how quickly a function is changing over time. So,  $\begin{array}{r}{x}^{\mathrm{\prime }}(t)\end{array}$ is the change in  $\begin{array}{r}x\end{array}$ values, and  $\begin{array}{r}{y}^{\mathrm{\prime }}(t)\end{array}$ is the change in  $\begin{array}{r}y\end{array}$ values for the parametric function $\begin{array}{r}F(t)=(x(t),y(t))\end{array}$ as  $\begin{array}{r}t\end{array}$ moves from  $\begin{array}{r}a\end{array}$ to $\begin{array}{r}b\end{array}$ .
  ::参数形曲线长度的方程式是 : Lab(x}(t))2+(yä(t))2dt。 记住, 衍生函数会显示函数随时间变化的速度。 因此, x(t) 是 x 值的变化, y`(t) 是参数函数F(t)=(x(t)),y(t)) 的y值变化, 从 t 移动到 b 。

  播放段落

  Let's find the length of the following curve between  $\begin{array}{r}t=1\end{array}$ and $\begin{array}{r}t=3\end{array}$ .
  ::让我们找到t=1和t=3之间的以下曲线长度。

  播放段落

  $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =4t\\ y(t)& =-t^2\end{array}$$

  
  ::F(t) = (x(t) y(t) ) x(t) = 4ty(t) t2

  播放段落

  First, set up your integral, using the distance formula you just learned.
  ::首先,用你刚学的距离公式 设置你的内装件

  播放段落

  $$\begin{array}{rl}L& =\underset{a}{\overset{b}{\int }}\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t){)}^2}dt\\ L& =\underset{1}{\overset{3}{\int }}\sqrt{(4{)}^2+(-2t{)}^2}dt\\ L& =\underset{1}{\overset{3}{\int }}\sqrt{16+4t^2}dt=\underset{1}{\overset{3}{\int }}2\sqrt{4+t^2}dt\end{array}$$

  
  ::Lab(x_(t))2+(y_(t))2+(y_(t))2dtL13(4)2+(-2t)2dtL1316+4t2dt1324+t2dt

  播放段落

  At this point you will need to use the formula for integrating expressions of the form $\begin{array}{r}\int \sqrt{a^2+u^2}du\end{array}$ , which is $\begin{array}{r}\int \sqrt{a^2+u^2}du=\frac{1}{2}u\sqrt{a^2+u^2}+\frac{a^2}{2}\ln \left|u+\sqrt{a^2+u^2}\right|\end{array}$ .
  ::在此点上, 您需要使用公式来整合窗体 {a2+u2du 的表达式, 即{a2+u2du=12ua2+u2+a22lnu+a2+u2}。

  播放段落

  So:
  ::因此:

  播放段落

  $\begin{array}{r}\underset{1}{\overset{3}{\int }}2\sqrt{4+t^2}dt=2{\left[\frac{t}{2}\sqrt{4+t^2}+\frac{4}{2}\ln \left|t+\sqrt{4+t^2}\right|\right]}_1^3\end{array}$ . Now, evaluate at 3 and 1 and subtract. You will want to use a calculator for this!
  ::\\ 1324+t2dt=2[t24+t2+42ln}\\ t+4+T2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  $$\begin{array}{rl}\underset{1}{\overset{3}{\int }}2\sqrt{4+t^2}dt& =2{\left[\frac{t}{2}\sqrt{4+t^2}+\frac{4}{2}\ln \left|t+\sqrt{4+t^2}\right|\right]}_1^3\\ 2\left[\frac{3}{2}\sqrt{13}+2\ln \left|3+\sqrt{13}\right|\right]& =18.3683\\ 2\left[\frac{1}{2}\sqrt{5}+2\ln \left|1+\sqrt{5}\right|\right]& =6.9335\\ 18.3683-6.9335& =11.4348\end{array}$$

  
  ::1324+t2dt=2[t24+t2+42lnt+4+t2]132[3213+2ln}3+13}=18.3683[125+2ln}1+5}=6.933583_6.9335=11.4348

  播放段落

  The length is 11.4348 units.
  ::长度为11.4348个单位。

  播放段落

  A single curve can be parameterized in different ways, depending on how fast an object travels along it. If you don’t pay attention to an object’s speed, you may get wildly different measurements for a curve from two different parameterizations.  For instance, consider a circle with its center at the origin and a radius of 5. You can write an infinite number of parametric equations for this circle, and each equation will traverse the curve in a different way.
  ::单个曲线可以不同的方式参数化, 取决于一个对象沿它移动的速度。 如果您不注意一个对象的速度, 您可以从两个不同的参数化中获得完全不同的曲线测量结果。 例如, 考虑一个圆, 其中心位于原点, 半径为 5 。 您可以为此圆写出无限数量的参数方程式, 每个方程式会以不同的方式绕过曲线 。

  播放段落

  Take a look at the following two parameterizations.  
  ::查看以下两个参数。

  播放段落

  $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =5\cos (3t)\\ y(t)& =5\sin (3t)\\ \\ G(t)& =(x(t),y(t))\\ x(t)& =5\cos (8t)\\ y(t)& =5\sin (8t)\end{array}$$

  
  ::F( t) = (x( t) ,y( t) ) x( t) = 5cos( 3t) y( t) = 5sin( ( 3t) G( t) = (x( t) ,y( t) y( t) x( t) = 5cos( 8t) y( t) = 5sin( 8t) y( t) = 5sin( 8t)

  播放段落

  Let's find the length of the curve from  $\begin{array}{r}t=0\end{array}$ to  $\begin{array}{r}t=\pi \end{array}$ for each of  them.
  ::让我们为它们每个人找到从t=0到t=%的曲线长度。

  播放段落

  First, find the length of the first curve:
  ::首先,找到第一个曲线的长度 :

  播放段落

  $$\begin{array}{rl}& \underset{0}{\overset{\pi }{\int }}\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t){)}^2}dt\\ x^{\mathrm{\prime }}(t)& =-15\sin (3t)\\ y^{\mathrm{\prime }}(t)& =15\cos (3t)\\ & \underset{0}{\overset{\pi }{\int }}\sqrt{(-15\sin (3t){)}^2+(15\cos (3t){)}^2}dt\\ & =\underset{0}{\overset{\pi }{\int }}\sqrt{225{\sin }^2(3t)+225{\cos }^2(3t)}dt\\ & =\underset{0}{\overset{\pi }{\int }}15\sqrt{{\sin }^{2}3t+{\cos }^{2}3t}dt\\ {\sin }^2\theta +{\cos }^2\theta & =1\\ & =\underset{0}{\overset{\pi }{\int }}15\sqrt{1}dt\\ & =15\pi \end{array}$$

  
  ::0(x(t)) 2+(y(t)) 2dtx_(t) 15sin(3t) (3t) (3t) =15cos(3t) (15sin(3t)) 2+(15cos(3t) })2dt(02) 225sin2}(3t) +225cos2}(3t) }(3t) dt) dt(015sin2}3t+cos2}}3tdtsin2(3t) 2(cos) (10151dt=15}

  播放段落

  In  $\begin{array}{r}\pi \end{array}$ seconds, the first object travels  $\begin{array}{r}15\pi \end{array}$ units around the curve. This doesn't mean that the length of the curve is  $\begin{array}{r}15\pi \end{array}$ units!  Since the circumference of a circle is $\begin{array}{r}2\pi r\end{array}$ , this circle has a circumference of $\begin{array}{r}10\pi \end{array}$ . The object actually made 1.5 laps around the circle in  $\begin{array}{r}\pi \end{array}$ seconds.
  ::在 ° 秒内, 第一个对象的 15 ° 单位环绕曲线。 这并不意味着曲线的长度是 15 ° 单位 。 由于圆的环绕是 2 °r, 此圆的环绕为 10 ° 。 该对象在 ° 秒内在圆圈周围实际做了1.5 圈 。

  播放段落

  Now, repeat the process with $\begin{array}{r}G(t)\end{array}$ .
  ::现在, 用 G( t) 重复此进程 。

  播放段落

  $$\begin{array}{rl}& \underset{0}{\overset{\pi }{\int }}\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t{)}^2)}dt\\ x^{\mathrm{\prime }}(t)& =-40\sin (8t)\\ y^{\mathrm{\prime }}(t)& =40\cos (8t)\\ & =\underset{0}{\overset{\pi }{\int }}\sqrt{(-40\sin (8t){)}^2+(40\cos (8t){)}^2}dt\\ & =\underset{0}{\overset{\pi }{\int }}\sqrt{1600{\sin }^2(8t)+1600{\cos }^2(8t)}dt\\ & =\underset{0}{\overset{\pi }{\int }}40\sqrt{{\sin }^{2}8t+{\cos }^{2}8t}dt\\ {\sin }^2\theta +{\cos }^2\theta & =1\\ & =\underset{0}{\overset{\pi }{\int }}40\sqrt{1}dt\\ & =40\pi \end{array}$$

  
  ::0(x(t))2+(y(t)2)dtx_(t)40sin(8t)_(t)=40cos(8t)_(8t)_(-40sin(8t)2+(40cos(8t)_(01600sin2)_(8t)+1600cos2}(8t)+1600cos2}(8t)_(8t)dt040sin2}8t+cos2}_(8t)_(8t)__(t)_(t)_(t)_(t)_(t)_(_(_)_(_)_(__(8t)_(0)_(8t)_(d)_(l)+1600cos2}2}(40_(dt)=40_

  播放段落

  The second object travels  $\begin{array}{r}40\pi \end{array}$ units in  $\begin{array}{r}\pi \end{array}$ seconds, which means it completed 4 laps around the same circle.
  ::第二个物体在____秒内飞行40°C单位,即在同一圆圈内完成4圈。

  播放段落

  If you’ve taken a physics class, you may remember that the distance an object travels is equal to its velocity times the time. Velocity is a measure of both speed and direction. You can use the distance formula to compute the speed of objects traveling on a curve.  If you take the derivative of an object’s distance at a certain time, you’ll find its speed. Another way to put this is:
  ::如果您选择了物理类, 您可以记住, 物体飞行的距离等于其速度乘以时间。 速度是速度和方向的衡量标准。 您可以使用距离公式来计算在曲线上飞行的物体的速度。 如果您在某个时间将物体距离的衍生物取出, 你会找到它的速度。 另一种方法就是 :

  播放段落

  $$\begin{array}{rl}s(t)& =\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t){)}^2}\end{array}$$

  
  ::s(t) = (x_(t)) 2+(y_(t)) 2

  播放段落

  Using the formula from above and given the following parametric equation that describes an object’s path as a function of time, let's find the object’s speed when $\begin{array}{r}t=3\end{array}$ .
  ::使用上面的公式, 并给定以下的参数方程, 该方程将对象路径描述为时间函数, 我们从 t=3 中查找对象的速度 。

  播放段落

  $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =6\cos t\\ y(t)& =2\sin t\end{array}$$

  Start by finding  $\begin{array}{r}{x}^{\mathrm{\prime }}(t)\end{array}$ and $\begin{array}{r}{y}^{\mathrm{\prime }}(t)\end{array}$ . Use these values to calculate $\begin{array}{r}s(t)\end{array}$ .
  ::F( t) = (x( t) y( t) x( t) = 6cos* ty( t) = 2sin@ tStart 查找 x_( t) 和 y_( t) 。 使用这些值来计算 s( t) 。

  播放段落

  $$\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =-6\sin t\\ y^{\mathrm{\prime }}(t)& =2\cos t\\ s(t)& =\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t){)}^2}\\ s(t)& =\sqrt{(-6\sin (t){)}^2+(2\cos (t){)}^2}\\ & =\sqrt{36{\sin }^{2}t+4{\cos }^{2}t}\\ & =\sqrt{36{\sin }^2(3)+4{\cos }^2(3)}\\ & =2.1534\end{array}$$

  
  ::=2cos2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ -\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  At time = 3, the object is moving at 2.1534 units per second.
  ::当时间=3时,该物体以每秒2.1534个单位移动。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to compare the distances and speeds of two cars that have different maximum speeds. If the track is a circle 4 kilometers in diameter, two possible equations for this track are:
  ::早些时候,您被要求比较两辆最大速度不同的汽车的距离和速度。 如果音轨是直径4公里的圆形, 这个音轨的两个可能的方程式是:

  播放段落

  $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =4\cos (100t)\\ y(t)& =4\sin (100t)\\ \\ G(t)& =(x(t),y(t))\\ x(t)& =4\cos (200t)\\ y(t)& =4\sin (200t)\end{array}$$

  
  ::F( t) = (x( t) ,y( t) ) x( t) = 4cos( 100t) y( t) = 4sin( 100t) G( t) = (x( t) y( t) y( t) x( t) = 4cos( 200t) y( t) y( t) = 4sin( 200t)

  播放段落

  Use the distance formula and speed to compare the distances traveled and speeds of the cars at $\begin{array}{r}t=.5\end{array}$ , assuming that time is measured in terms of hours and distance is measured in kilometers.
  ::使用距离公式和速度来比较在t=5时行驶的距离和汽车速度,假设时间按小时和距离以公里计算。

  播放段落

  For the first car:
  ::第一辆车:

  播放段落

  $$\begin{array}{rl}& \underset{0}{\overset{.5}{\int }}\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t{)}^2)}dt\\ x^{\mathrm{\prime }}(t)& =-400\sin (100t)\\ y^{\mathrm{\prime }}(t)& =400\cos (100t)\\ & \underset{0}{\overset{.5}{\int }}\sqrt{(-400\sin (100t){)}^2+(400\cos (100t){)}^2}dt\\ & =\underset{0}{\overset{.5}{\int }}400\sqrt{{\sin }^2(100t)+{\cos }^2(100t)}dt\\ {\sin }^2\theta +{\cos }^2\theta & =1\\ & =\underset{0}{\overset{.5}{\int }}400\sqrt{1}dt\\ & =200km\\ s(t)& =\sqrt{(-400\sin (100t){)}^2+(400\cos (100t){)}^2}\\ & =400km/hr\end{array}$$

  
  ::0.5(x_(t))2+(y_(t)2)dtx}(t)400sin(100t)y(t)=400cos(100t) 0.5(-400sin(100t))2+(400cos(100t))2}2dt0.5400sin2(100t)+cos2(100t)dsin2(cos2)1_0.5001dt=200sm(t)=(400sin(100t))2+(400cos(100t))2=400公里/hr

  播放段落

  So, the first car travelled 200 km during a half-hour test drive, at a speed of 400 km/hr.
  ::因此,第一辆汽车在半个小时的试车中行驶200公里,每小时400公里。

  播放段落

  Now, compute the distance and speed traveled by the second car.
  ::现在,计算第二辆车行驶的距离和速度

  播放段落

  $$\begin{array}{rl}& \underset{0}{\overset{.5}{\int }}\sqrt{(x^{\mathrm{\prime }}(t){)}^2+(y^{\mathrm{\prime }}(t{)}^2)}dt\\ x^{\mathrm{\prime }}(t)& =-800\sin (200t)\\ y^{\mathrm{\prime }}(t)& =800\cos (200t)\\ & \underset{0}{\overset{.5}{\int }}\sqrt{(-800\sin (200t){)}^2+(800\cos (200t){)}^2}dt\\ & =\underset{0}{\overset{.5}{\int }}800\sqrt{{\sin }^2(200t)+{\cos }^2(200t)}dt\\ {\sin }^2\theta +{\cos }^2\theta & =1\\ & =\underset{0}{\overset{.5}{\int }}800\sqrt{1}dt\\ & =400km\\ s(t)& =\sqrt{(-800\sin (200t){)}^2+(800\cos (200t){)}^2}\\ & =800km/hr\end{array}$$

  
  ::0.5(x_(t))2+(y_(t)2)dt_(t) 800sin(200t)=800cos(200t) 0.5(800sin(200t))2+(800cos(200t))2dt0.5800sin2(200t)+cos2}(200t)dtsin2}(200t)dtsin2}2210.58001dt=400ks(t)=(800sin(200t))2+(800cos(200t))2=800k/hr

  播放段落

  The second car traveled 400 km at 800 km/hr. That means that while the first car was a very fast sports car, the second car was travelling at ‘rocket-car’ speeds, though not fast enough to beat the world land speed record.
  ::第二辆汽车以800公里/小时的速度行驶了400公里。 这意味着虽然第一辆汽车是一辆非常快的运动车,但第二辆汽车正在以 " 火箭车 " 速度行驶,虽然速度不足以打破世界陆地速度记录。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the length of the following curve from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=5\end{array}$ .
  ::查找以下曲线的长度,从 t=0 到 t=5。

  播放段落

  $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =4t^2\\ y(t)& =2t^3\end{array}$$

  
  ::F(t) = (x(t) y(t) ) x(t) = 4t2y(t) = 2t3

  播放段落

  Start by finding the :
  ::以发现:

  播放段落

  $$\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =8t\\ y^{\mathrm{\prime }}(t)& =6t^2\end{array}$$

  
  ::x_(t)=8ty_(t)=6t2

  播放段落

  Now, set up the integral for the distance equation.
  ::现在 设置距离方程的内装件

  播放段落

  $$\begin{array}{rl}& \underset{0}{\overset{5}{\int }}\sqrt{(8t{)}^2+(6t^2{)}^2}dt\\ & \underset{0}{\overset{5}{\int }}\sqrt{64t^2+36t^4}dt\end{array}$$

  
  ::@ 05( 8t) 2+( 6t2) 2dt @ 0564t2+36t4dt

  播放段落

  Factor, simplify, and then substitute.
  ::因素,简化,然后替代。

  播放段落

  $$\begin{array}{rl}& \underset{0}{\overset{5}{\int }}\sqrt{64t^2+36t^4}dt\\ & =\underset{0}{\overset{5}{\int }}\sqrt{(4t^2)(16+9t^2)}dt\\ & =\underset{0}{\overset{5}{\int }}2t\sqrt{(16+9t^2)}dt\\ u& =(16+9t^2)\\ du& =18tdt\\ 2tdt& =\frac{du}{9}\\ & =\int \frac{1}{9}(u{)}^{\frac{1}{2}}du\end{array}$$

  
  ::0564t2+36t4dt05(4t2)(16+9t2)dt052t(16+9t2)dtu=(16+92)dtu=(16+92)dtu=18t dt2t dt=du9}19(u)12du

  播放段落

  Now, integrate.
  ::现在,整合。

  播放段落

  $$\begin{array}{rl}\int \frac{1}{9}(u{)}^{\frac{1}{2}}du& =\frac{1}{9}\left[\frac{2}{3}{u}^{\frac{3}{2}}\right]\\ & =\frac{1}{9}{\left[\frac{2}{3}(16+9t^2{)}^{\frac{3}{2}}\right]}_0^5\\ & =\frac{1}{9}\left[\left[\frac{2}{3}(16+9(5^2){)}^{\frac{3}{2}}\right]-\left[\frac{2}{3}(16+9(0^2){)}^{\frac{3}{2}}\right]\right]\\ & =272.395\end{array}$$

  
  ::19(u)12du=19[23u32]=19[23(16+9T232)32]05=19[[23(16+9(52)32]-[23(16+9(02)32]]]]=272.395]

  播放段落

  The curve is 272.395 units long.
  ::曲线是272.395单位长。

  播放段落

  Example 3
  ::例3

  播放段落

  Calculate the speed of an object traveling the curve in # 1 at  $\begin{array}{r}t=0\end{array}$ and at $\begin{array}{r}t=5\end{array}$ .
  ::在 t=0 和 t=5 中计算一个在# 1 中运行的曲线对象的速度。

  播放段落

  Speed is the rate at which distance is changing. You can find the speed using the square root of the sum of the derivatives.
  ::速度是距离变化的速度。您可以使用衍生物总和的平方根找到速度。

  播放段落

  $$\begin{array}{rl}s(t)& =\sqrt{(8t{)}^2+(6t^2{)}^2}\\ s(5)& =\sqrt{(40{)}^2+(150{)}^2}=155.242\\ s(0)& =\sqrt{0}=0.\end{array}$$

  
  ::s(t) = (8t) 2+(6t2)2s(5)=(40)2+(150)2=155.242s(0)=0=0。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the length of the curve from  $\begin{array}{r}t=0\end{array}$ to  $\begin{array}{r}t=\frac{\pi }{6}\end{array}$ for the following circle. Then find the speed when $\begin{array}{r}t=\frac{\pi }{6}\end{array}$ .
  ::查找以下圆的曲线长度, 从 t=0 到 t6 。 然后查找t6 时的速度 。

  播放段落

  $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =5\cos 2t\\ y(t)& =5\sin 2t\end{array}$$

  
  ::F( t) = (x( t) y( t) ) x( t) = 5cos @ @ 2ty( t) = 5sin @ 2t

  播放段落

  Find the derivatives, evaluate the radical to find speed, and integrate to find distance.
  ::寻找衍生物,评估激进 以寻找速度, 整合以寻找距离。

  播放段落

  $$\begin{array}{rl}{x}^{\mathrm{\prime }}(t)& =-10\sin 2t\\ y^{\mathrm{\prime }}(t)& =10\cos 2t\\ s(t)& =\sqrt{(-10\sin 2t{)}^2+(10\cos 2t{)}^2}\\ s\left(\frac{\pi }{6}\right)& =\sqrt{{\left(\frac{10\sqrt{3}}{2}\right)}^2+(5{)}^2}\\ s\left(\frac{\pi }{6}\right)& =\sqrt{100}\\ s\left(\frac{\pi }{6}\right)& =10\end{array}$$

  
  ::x>( t) 10sin2ty}( t) =10cos2ts( t) =( - 10sin2t) 2+( 10cos2t) 2s( 6) =( 1032) 2+(5)2s( 6) =100s( 6) =10

  播放段落

  The speed at  $\begin{array}{r}t=\frac{\pi }{6}\end{array}$ is 10.
  ::速度在t6是10。

  播放段落

  $$\begin{array}{rl}d& =\underset{0}{\overset{\frac{\pi }{6}}{\int }}\sqrt{(-10\sin 2t{)}^2+(10\cos 2t{)}^2}dt\\ d& =10\underset{0}{\overset{\frac{\pi }{6}}{\int }}\sqrt{{\sin }^{2}2t+{\cos }^{2}2t}dt\\ d& =10\underset{0}{\overset{\frac{\pi }{6}}{\int }}\sqrt{1}dt=10\left(\frac{\pi }{6}\right)\\ d& =\frac{5\pi }{3}\end{array}$$

  
  ::d06(- 10sin2t) 2+( 10cos2t) 2ddd=1006sin22}2t+cos22}2ttdtddd=10061dt=10( 6)d=53

  播放段落

  The distance traveled between  $\begin{array}{r}t=0\end{array}$ and  $\begin{array}{r}t=\frac{\pi }{6}\end{array}$ is  $\begin{array}{r}\frac{5\pi }{3}\end{array}$ units.
  ::t=0和t=6之间的距离是5+3个单位。

  播放段落

  Review
  ::回顾

  播放段落
  1. Find the length of the following curve from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=4\end{array}$ .
     $$\begin{array}{rl}F(t)& =(x(t),y(t))\\ x(t)& =t+1\\ y(t)& =2t^2+3\end{array}$$
     
     ::查找以下曲线的长度, 从 t=0 到 t=4. F( t) = (x( t, y( t) ) x( t) = t+1y( t) = 2t2+3
  播放段落
  2. Find the length of the following curve from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=5\end{array}$ .
     $$\begin{array}{rl}G(t)& =(x(t),y(t))\\ x(t)& =3t^{\frac{3}{2}}\\ y(t)& =\frac{1}{2}{t}^2\end{array}$$
     
     ::查找以下曲线的长度, 从 t=0 到 t=5. G( t) = (x( t),y( t) y( t) ) x( t) = 3t32y( t) = 12t2
  播放段落
  3. Find the length of the following curve from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=2\pi \end{array}$ .
     ::查找以下曲线的长度,从 t=0 到 t=2。

  播放段落

  $$\begin{array}{rl}H(t)& =(x(t),y(t))\\ x(t)& =\sin (t)-t\cos (t)\\ y(t)& =\cos (t)+t\sin (t)\end{array}$$

  
  ::H(t) = (x(t) y(t) ) x(t) =sin(t) -tcos(t) y(t) =cos(t) +tsin(t)

  播放段落
  4. Find the length of the following curve from  $\begin{array}{r}t=\frac{\pi }{4}\end{array}$ to $\begin{array}{r}t=\frac{\pi }{2}\end{array}$ .
     $$\begin{array}{rl}J(t)& =(x(t),y(t))\\ x(t)& =4\cos \left(\frac{t}{2}\right)\\ y(t)& =4\sin \left(\frac{t}{2}\right)\end{array}$$
     
     ::查找以下曲线的长度, 从 t4 到 t2. J( t) = (x( t),y( t)) x( t) = 4cos( t2) y( t) = 4sin( t2)
  播放段落
  5. Find the length of the following curve from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=\pi \end{array}$ .
     $$\begin{array}{rl}J(t)& =(x(t),y(t))\\ x(t)& =e^t\sin (t)\\ y(t)& =e^t\cos (t)\end{array}$$
     
     ::查找以下曲线的长度, 从 t=0 到 t. J( t) = (x( t),y( t) ) x( t) =etsin ( t) y( t) =etcos( t)
  播放段落
  6. Calculate the speed of an object traveling the curve in #1 at $\begin{array}{r}t=4\end{array}$ .
     ::计算在 t=4 处行驶于# 1 曲线中的对象的速度。
  播放段落
  7. Calculate the speed of an object traveling the curve in #2 at $\begin{array}{r}t=5\end{array}$ .
     ::计算在 t=5 处行驶于# 2 曲线中的物体的速度。
  播放段落
  8. Calculate the speed of an object traveling the curve in #3 $\begin{array}{r}t=2\pi \end{array}$ .
     ::计算在 # 3 t= 2 中运行曲线的物体的速度。
  播放段落
  9. Calculate the speed of an object traveling the curve in #4 at $\begin{array}{r}t=\frac{\pi }{4}\end{array}$ .
     ::计算在 t++++4 中以#4 移动曲线的物体的速度。
  播放段落
  10. Calculate the speed of an object traveling the curve in #5 at $\begin{array}{r}t=\frac{\pi }{2}\end{array}$ .
      ::计算在 t2 2 5 中运行曲线的物体的速度。
  播放段落
  11. Derive the formula for the circumference of a circle by finding the length of the following curve from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=2\pi \end{array}$ .
      ::通过发现以下曲线的长度,从t=0到t=2,得出圆环形的公式。
  播放段落
  12. $$\begin{array}{rl}M(t)& =(x(t),y(t))\\ x(t)& =r\cos (t)\\ y(t)& =r\sin (t)\end{array}$$
      
      :t)=(x(t),y(t))x(t)=rcos(t)y(t)=rsin(t)

  播放段落

  For #12-14, consider the curve defined by:
  ::第12-14号,请考虑以下曲线的定义:

  播放段落

  $$\begin{array}{rl}N(t)& =(x(t),y(t))\\ x(t)& =4\cos t\\ y(t)& =7\sin t+1\end{array}$$

  
  :t)=(x(t),y(t))x(t)=4costy(t)=7sint+1

  播放段落
  12. What type of curve is this? How long would an object need to travel to make its way around the curve?
      ::这是什么类型的曲线? 物体需要经过多久才能绕过曲线?
  播放段落
  13. Find the length of the entire curve.
      ::查找整个曲线的长度。
  播放段落
  14. Find the speed of an object traveling the curve at $\begin{array}{r}t=\frac{\pi }{2}\end{array}$ .
      ::查找在 t2 处移动曲线对象的速度 。
  播放段落
  15. Find the arc length of the following from  $\begin{array}{r}t=0\end{array}$ to $\begin{array}{r}t=\pi \end{array}$ .
      ::查找从 t=0 到 t 的以下值的弧长度 。

  播放段落

  $$\begin{array}{rl}P(t)& =(x(t),y(t))\\ x(t)& =2{\cos }^5(t)\\ y(t)& =2{\sin }^5(t)\end{array}$$

  
  ::P( t) = (x( t) ,y( t) ) x( t) = 2cos5 ( t) y( t) = 2sin5 ( t)

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。