课程： 10.16 极表和微积分:革命量

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节极表和微积分:革命的量

折叠展开
极表和微积分:革命的量
Matthias has made a bowl that can be described as the revolution of one quarter of the curve $\begin{aligned} r = 5 \cos θ \end{aligned}$ . How much liquid can the bowl hold?
::Matthias做了一个碗,可以说是四分之一的曲线 r=5cos的革命。碗能装多少液体?

Volume of Revolution Using Polar Forms
::使用极地形式的革命量

Finding volumes for revolutions in polar form can be difficult. The variables $\begin{aligned} r \end{aligned}$ and $\begin{aligned} θ \end{aligned}$ don’t interact in a way that allows you to easily divide complex solids into cylindrical slices. If you continue on in mathematics, you’ll learn how to find the volumes of complex solids using a double integral. However, there are certain polar curves that lend themselves to easier calculations.
::以极地形式寻找革命的量可能很困难。变量 r 和无法以方便的方式将复杂的固体分为圆柱形切片。如果你继续数学,你就会学会如何使用双元集成找到复杂的固体量。但是,某些极地曲线可以更容易地进行计算。

To find the volume of a polar curve rotated about an axis, you’ll need to put the equation back in rectangular form in terms of $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . After you’ve transformed the equation, you can use the formula for the volume of a rotation around an axis in three dimensions to find the volume of the solid.
::要找到在轴上旋转的极曲线的体积, 您需要将方程的矩形以 x 和 y 的形式重新放回。在您转换了方程后, 您可以使用三个维的轴周围旋转的方程式, 以找到固体的体积。

Usually, the most difficult part of these problems is transforming from polar form to rectangular form. Once you’ve mastered that aspect of the problem, you’ll be able to find the volume.
::通常,这些问题中最困难的部分是从极形转变为矩形。一旦你掌握了这个问题的这一方面,你就能找到其体积。

Let's find the volume of the curve $\begin{aligned} r = 10 \end{aligned}$ revolved around the polar axis from 0 to $\begin{aligned} π \end{aligned}$ .
::让我们找到圆轴 r=10的音量从0到 ° 围绕极轴旋转

This is an equation for a circle with a radius of 10, so the revolution will produce a sphere. To find the volume, you’ll first need to put the equation into rectangular form using one of the polar identities. In this case, you can use the transformation $\begin{aligned} r^{2} = x^{2} + y^{2} \end{aligned}$ , which comes from placing the polar axis along the $\begin{aligned} x \end{aligned}$ -axis, the origin at the origin, and then using the Pythagorean theorem.
::这是一个半径为 10 的圆形方程式, 因此革命将产生一个球体。要找到音量, 您首先需要使用极特性之一将方程式以矩形形式设置为矩形。在此情况下, 您可以使用转换 r2=x2+y2 , 它来自将极轴置于 X 轴上, 原原点为 X 轴, 然后使用 Pythagorian 定理。

$\begin{aligned} r & = 10 \\ r^{2} & = x^{2} + y^{2} \\ 10^{2} & = x^{2} + y^{2} \\ 100 & = x^{2} + y^{2} \end{aligned}$

::r=10r2=x2+y2102=x2+y2102=x2+y2100=x2+y2

To find the volume for a revolution around the $\begin{aligned} x \end{aligned}$ -axis, you’ll need to use the formula: $\begin{aligned} V = π \int {(f (x))}^{2} d x \end{aligned}$ . This will allow you to find the volumes of infinitely thin slices of the solid, and then add them all together to find the total volume.
::要在 x 轴周围找到革命的音量, 您需要使用公式 : V( f (x)) 2dx 。这将允许您找到无限薄的固体片的音量, 然后将它们加在一起以找到总音量。

To use this equation, you’ll first need to express $\begin{aligned} y \end{aligned}$ in terms of $\begin{aligned} x \end{aligned}$ .
::使用这个方程式, 您首先需要以 x 表示 y 。

$\begin{aligned} x^{2} + y^{2} & = 100 \\ y^{2} & = 100 - x^{2} \\ \sqrt{y^{2}} & = \sqrt{100 - x^{2}} \\ y & = \pm \sqrt{100 - x^{2}} \end{aligned}$

::x2+y2 = 100y2 = 100-x2y2 = 100-x2y2 = 100-x2y__100-x2y__100-x2

Since the revolution of a semi-circle and the revolution of a circle will both produce the same sphere, you can just work with the positive half of the equation above. Also, since a circle centered at the origin is symmetrical around the $\begin{aligned} y \end{aligned}$ axis, you can integrate from 0 to 10 (the radius of the semicircle) and then simply double the volume. So, you can set up your integral like this:
::由于半圆形的革命和圆圈的革命将产生相同的球体, 您可以使用上面正方程的正半数来工作。另外, 由于以原为中心的一个圆形在 y 轴上对称, 您可以从 0 到 10 个( 半圆形半径) 整合, 然后将体积翻一番。因此, 您可以设置这样的整体体 :

$\begin{aligned} V = 2 π \int_{0}^{10} {(\sqrt{100 - x^{2}})}^{2} d x \end{aligned}$

::V=2010(100-x2)2dx

Now, integrate and find the volume.
::现在,整合并找到音量。

$\begin{aligned} V & = 2 π \int_{0}^{10} {(\sqrt{100 - x^{2}})}^{2} d x \\ = 2 π \int_{0}^{10} 100 - x^{2} d x \\ = 2 π {[100 x - \frac{1}{3} x^{3}]}_{0}^{10} \\ = \frac{4000 π}{3} u n i t s^{3} \end{aligned}$

::V=2010(100-x2)2dx=2010100-x2dx=2}[100x-13x3]010=400%3单位3]

Notice that the geometric formula for the volume of the sphere is $\begin{aligned} \frac{4}{3} π r^{3} \end{aligned}$ . So, using integrals to find the volume of a sphere will give you the same result as using the geometric method to find volume.
::注意球体体积的几何公式是43°r3。所以,使用整体体来查找球体体积, 将会给您带来与使用几何方法来查找体积相同的结果。

In the problem above, you transformed a very simple polar equation into rectangular form so that you could rotate it and find its volume. Now, you’re ready to tackle a slightly more difficult equation.
::在上述问题中,你将一个非常简单的极方方程转换成长方形,这样你就可以旋转它并找到它的体积。现在,你准备处理一个略为困难的方程。

Let's find the volume of the solid formed when you revolve the polar equation $\begin{aligned} r = 4 \sin θ \end{aligned}$ around the line $\begin{aligned} θ = \frac{π}{2} \end{aligned}$ .
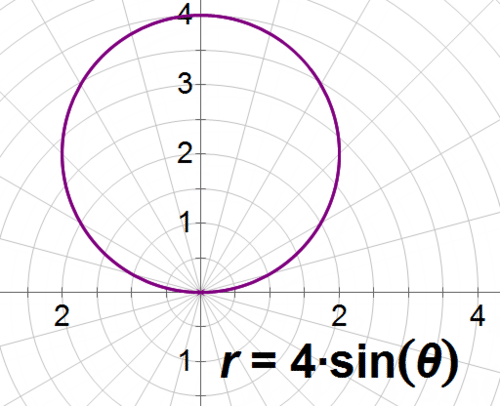
::让我们来找找固体的体积当你在2号线周围旋转极方程式 r=4sin。

If you sketch this equation, you’ll see that it’s a circle with a center at $\begin{aligned} (2, \frac{π}{2}) \end{aligned}$ and a radius of 2.
::如果你勾画这个方程式, 你会看到它是一个圆形,中心在2,2,2,2,半径。

To transform this equation into rectangular form, you’ll have to make use of the identity $\begin{aligned} r \sin θ = y \end{aligned}$ in addition to $\begin{aligned} r^{2} = x^{2} + y^{2} \end{aligned}$ .
::要将方程式转换成矩形, 您除了 r2=x2+y2 外, 还必须使用身份 rsiny 。

$\begin{aligned} r & = 4 \sin θ \\ r^{2} & = 4 r \sin θ \\ x^{2} + y^{2} & = 4 y \end{aligned}$

::r=4sinr2=4rsinx2+y2=4y

You’ll be revolving the curve around the line $\begin{aligned} θ = \frac{π}{2} \end{aligned}$ . This is equivalent to the $\begin{aligned} y \end{aligned}$ -axis in rectangular form. Since you’re revolving the curve around the $\begin{aligned} y \end{aligned}$ -axis, you’ll want to use the volume formula for a revolution around the $\begin{aligned} y \end{aligned}$ -axis: %20%5Cright%20)%5E2%20dy"> $\begin{aligned} V = π \int {(f (y))}^{2} d y \end{aligned}$ . You’re integrating in terms of $\begin{aligned} y \end{aligned}$ because when you revolve a curve around the $\begin{aligned} y \end{aligned}$ -axis, the radius of each disc is $\begin{aligned} x \end{aligned}$ , and the height of each disk is $\begin{aligned} d y \end{aligned}$ . To continue, you will need to express $\begin{aligned} x \end{aligned}$ in terms of $\begin{aligned} y \end{aligned}$ :
::将曲线旋转到 2 线周围。这相当于 y 轴的矩形 y 轴。由于您环绕 y 轴旋转曲线, 您需要使用 y 轴周围 y 轴的音量公式 : V (f)2dy 。您正在整合 y , 因为当您绕着 y 轴旋转时, 每个盘的半径是 x , 每个盘的高度是 y 轴。要继续, 您需要用 y 字表示 x :

$\begin{aligned} 4 y & = x^{2} + y^{2} \\ x^{2} & = 4 y - y^{2} \\ x & = \pm \sqrt{4 y - y^{2}} \end{aligned}$

::4y =x2+y2x2=4y-y2x*4y-y2

Since the circle is symmetrical around the $\begin{aligned} y \end{aligned}$ -axis, you only need to use the right half of the curve in your integral in order to find the volume of the entire solid. From your sketch, you can see that you’ll need to integrate from $\begin{aligned} y = 0 \end{aligned}$ to $\begin{aligned} y = 4 \end{aligned}$ . So,
::由于圆环在 Y 轴周围对称, 您只需要使用整体中曲线的右半角才能找到整个固体的体积。从您的草图中, 您可以看到您需要从 y=0 到 y=4 整合。所以,

$\begin{aligned} V & = π \int_{0}^{4} {(\sqrt{4 y - y^{2}})}^{2} d y \\ = π \int_{0}^{4} 4 y - y^{2} d y \\ = π {[2 y^{2} - \frac{1}{3} y^{3}]}_{0}^{4} \\ = π [32 - \frac{64}{3}] \\ = \frac{32 π}{3} u n i t s^{3} \end{aligned}$

::V*04(4y-y2)2dy044y-y2dy[2y2-13y3]04[32-643]=3283单位3]

Examples
::实例

Example 1
::例1

Earlier, you were asked how Matthias can find the volume of his bowl. To find the volume of his bowl, Matthias will first have to put the equation describing the bowl into rectangular form.
::早些时候,有人问你Matthias如何找到碗的容量。为了找到碗的容量,Matthias必须首先将描述碗的方程式以矩形形式排列。

$\begin{aligned} r & = 5 \cos θ \\ r^{2} & = 5 r \cos θ \\ x^{2} + y^{2} & = 5 x \end{aligned}$

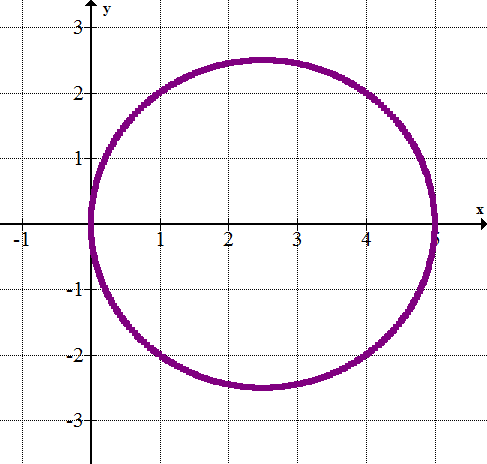
::r=5cosr2=5rcosx2+y2=5x

He now has the equation for a circle with a center at (2.5, 0) and a radius of 2.5. If he revolves half of the top half of the circle around the $\begin{aligned} x \end{aligned}$ -axis, he’ll have a model for his bowl.
::他现在拥有一个圆的方程式,圆的中心(2.5,0)和半径2.5。如果他在X轴周围旋转圆顶半部的一半,他就会有一个碗的模型。

To revolve the curve, he’ll first need to express $\begin{aligned} y \end{aligned}$ in terms of $\begin{aligned} x \end{aligned}$ .
::他首先需要以x表示y。

$\begin{aligned} 5 x & = x^{2} + y^{2} \\ y^{2} & = 5 x - x^{2} \\ y & = \pm \sqrt{5 x - x^{2}} \end{aligned}$

::5x=x2+y2y2=5x-x2y=5x-x2y=5x-x2y=5x-x2x-x2

Since he wants to model the shape of his bowl, he'll only need to integrate the positive side of the equation from 0 to 2.5.
::既然他想模拟碗的形状他只需要将正方程的一面从0到2.5

$\begin{aligned} V & = π \int_{0}^{2.5} {(\sqrt{5 x - x^{2}})}^{2} d x \\ = π \int_{0}^{2.5} 5 x - x^{2} d x \\ = π {[\frac{5}{2} x^{2} - \frac{1}{3} x^{3}]}_{0}^{2.5} \\ = 10.4167 π \end{aligned}$

::V02.5(5x-x2)2dx02.55x-x2dx}[52x2-13x3]02.5=10.4167]

His bowl can hold $\begin{aligned} 10.4167 π u n i t s^{3} \end{aligned}$ of liquid.
::他的碗能装有10.4167瓦单位3的液体

Example 2
::例2

Convert the equation $\begin{aligned} r = \frac{1}{4 \sin θ + 2 \cos θ} \end{aligned}$ into rectangular form, then revolve it around the $\begin{aligned} x \end{aligned}$ -axis from 0 to 5.
::将方程式 r= 14sin2cos 转换成矩形,然后围绕 X 轴从 0 向 5 旋转。

Remember that $\begin{aligned} r \sin θ = y \end{aligned}$ and $\begin{aligned} r \cos θ = x \end{aligned}$ . Cross multiply, substitute, and then solve for $\begin{aligned} y \end{aligned}$ :
::记住rsiny 和 rcosx。交叉乘法, 替代, 然后解决 y :

$\begin{aligned} r & = \frac{1}{4 \sin θ + 2 \cos θ} \\ r (4 \sin θ + 2 \cos θ) & = 1 \\ 4 r \sin θ + 2 \cos θ & = 1 \\ 4 y + 2 x & = 1 \\ y & = - \frac{1}{2} x + \frac{1}{4} \end{aligned}$

::r=14sin2cosr( 4sin2cos) =14sin2cos14y+2x=1y12x+14

You now have the equation for a line in $\begin{aligned} y = m x + b \end{aligned}$ form. If you look at a sketch of the graph, you’ll see that the revolution from 0 to 5 will produce a double cone.
::您现在有了y=mx+b 形式的线条的方程式。如果您看一下图形的草图, 你会看到从 0 到 5 的革命将产生双锥体。

Use the volume formula and solve to find the volume of the solid produced by the revolution.
::使用体积公式和解析法找到革命产生的固体体积

$\begin{aligned} V & = π \int_{0}^{5} {(- \frac{1}{2} x + \frac{1}{4})}^{2} d x \\ = π \int_{0}^{5} (\frac{1}{4} x^{2} - \frac{1}{4} x + \frac{1}{16}) d x \\ = π {[\frac{1}{12} x^{3} - \frac{1}{8} x^{2} + \frac{1}{16} x]}_{0}^{5} \\ = π [\frac{1}{12} (5)^{3} - \frac{1}{8} (5)^{2} + \frac{1}{16} (5)] \\ = \frac{365 π}{48} u n i t s^{3} \end{aligned}$

::V05(- 12x+14) 2dx05( 14x2- 14x+116) dx[ 112x3- 18x2+116x] 05}[112(5)3- 18(5)2+116(5)] =365- 48单位3]

Example 3
::例3

Put the equation $\begin{aligned} r = 6 \end{aligned}$ into rectangular form and then find the volume of its revolution around the $\begin{aligned} x \end{aligned}$ -axis from 3 to 5.
::将 r=6 方程式以矩形形式排列,然后在 3 到 5 的 x 轴周围找到它的革命量。

Put the equation into rectangular form, and write it in terms of $\begin{aligned} y \end{aligned}$ :
::将方程式以矩形形式显示, 并用 y 写成 :

$\begin{aligned} r & = 6 \\ r^{2} & = x^{2} + y^{2} \\ 36 & = x^{2} + y^{2} \\ y^{2} & = 36 - x^{2} \\ y & = \pm \sqrt{36 - x^{2}} \end{aligned}$

::r=6r2=x2+y236=x2+y2y2=36-x2y36-x2

Now, use the volume formula:
::现在,使用音量公式:

$\begin{aligned} V & = π \int_{3}^{5} {(\sqrt{36 - x^{2}})}^{2} d x \\ = π \int_{3}^{5} 36 - x^{2} d x \\ = π {[36 x - \frac{1}{3} x^{3}]}_{3}^{5} \\ = \frac{118 π}{3} \end{aligned}$

::V35(36-x2)2dx3536-x2dx[36x-13x3]35=1183]

The volume is $\begin{aligned} \frac{118 π}{3} u n i t s^{3} \end{aligned}$ .
::卷号为118 3单位3。

Example 4
::例4

Put the equation $\begin{aligned} r = 2 \sin θ \end{aligned}$ into rectangular form, then revolve it around the $\begin{aligned} y \end{aligned}$ -axis from $\begin{aligned} y = 0 \end{aligned}$ to $\begin{aligned} y = 1 \end{aligned}$ and find the volume.
::将方程式 r= 2sin 以矩形形式显示, 然后围绕 Y 轴从 y=0 到 y =1 旋转, 然后找到音量。

Multiply both sides of the equation by $\begin{aligned} r \end{aligned}$ , then use $\begin{aligned} y = r \sin θ \end{aligned}$ and $\begin{aligned} r^{2} = x^{2} + y^{2} \end{aligned}$ . Then, solve for $\begin{aligned} x \end{aligned}$ :
::将方程式两边乘以 r, 然后使用 y=rsin 和 r2=x2+y2。然后, 解答 x:

$\begin{aligned} r & = 2 \sin θ \\ r^{2} & = 2 r \sin θ \\ r^{2} & = 2 y \\ 2 y & = x^{2} + y^{2} \\ 2 y - y^{2} & = x^{2} \\ \pm \sqrt{2 y - y^{2}} & = x \end{aligned}$

::r2=2rsinr2=2y2y2y=x2+y22y-y2=x2_y2=x2_2y_y2=2rsin_r2=2rsin}r2=2y2y2y=x

Now use the volume formula:
::现在使用音量公式 :

$\begin{aligned} V & = π \int_{0}^{1} {(\sqrt{2 y - y^{2}})}^{2} d y \\ = π \int_{0}^{1} 2 y - y^{2} d y \\ = π {[y^{2} - \frac{1}{3} y^{3}]}_{0}^{1} \\ = \frac{2 π}{3} \end{aligned}$

::V#01(2y-y2)2dy012y-y2dy[y2-13y3]01=23

The volume is $\begin{aligned} \frac{2 π}{3} u n i t s^{3} \end{aligned}$ .
::体积为2×3单位3。

Example 5
::例5

Put the equation $\begin{aligned} r = \frac{5}{3 \sin θ - 4 \cos θ} \end{aligned}$ into rectangular form, then revolve it around the $\begin{aligned} x \end{aligned}$ -axis from 0 to 2 and find the volume of the revolution.
::将 r= 53sin4cos 方程式以矩形形式排列, 然后围绕 X 轴从 0 到 2 旋转, 并找到革命的量。

First put the equation into rectangular form and solve for $\begin{aligned} y \end{aligned}$ :
::首先将方程式以矩形形式放入正方形,然后为 y 求解 :

$\begin{aligned} r & = \frac{5}{3 \sin θ - 4 \cos θ} \\ 3 r \sin θ - 4 r \cos θ & = 5 \\ 3 y - 4 x & = 5 \\ 3 y & = 4 x + 5 \\ y & = \frac{4}{3} x + \frac{5}{3} \end{aligned}$

::r = 53sin=4cos 4cos 3rsin=4cos 4rcos *53y-4x=53y=4x+5y=43x+53

Now, use the volume formula.
::现在,使用音量公式。

$\begin{aligned} V & = π \int_{0}^{2} {(\frac{4}{3} x + \frac{5}{3})}^{2} d x \\ = π \int_{0}^{2} \frac{16}{9} x^{2} + \frac{40}{9} x + \frac{25}{9} d x \\ = π {[\frac{16}{27} x^{3} + \frac{40}{18} x^{2} + \frac{25}{9} x]}_{0}^{2} \\ = \frac{518 π}{27} \end{aligned}$

::V02( 43x+53)2dx02169x2+409x+259dx[1627x3+4018x2+259x]02=518__27]

The volume is $\begin{aligned} \frac{518 π}{27} u n i t s^{3} \end{aligned}$ .
::体积为518 27单位3。

Review
::回顾

Put the equation $\begin{aligned} r = 4 \end{aligned}$ into rectangular form and then find the volume of its revolution around the $\begin{aligned} x \end{aligned}$ -axis from 1 to 3.
::将 r=4 方程式以矩形形式排列,然后在 1 到 3 的 x 轴周围找到它的革命量。

Put the equation $\begin{aligned} r = 2 \end{aligned}$ into rectangular form and then find the volume of its revolution around the $\begin{aligned} y \end{aligned}$ -axis from 1 to 2.
::将 r=2 方程以矩形形式排列,然后在 Y 轴 1 到 2 周围发现其革命的量。

Put the equation $\begin{aligned} r = 8 \end{aligned}$ into rectangular form and then find the volume of its revolution around the $\begin{aligned} y \end{aligned}$ -axis from -8 to 8.
::将 r=8 方程以矩形形式排列,然后在 - 8 到 8 之间找到Y 轴周围的革命量。

Put the equation $\begin{aligned} r = a \end{aligned}$ into rectangular form and then find the volume of its revolution around the $\begin{aligned} x \end{aligned}$ -axis from $\begin{aligned} - a \end{aligned}$ to $\begin{aligned} a \end{aligned}$ . What does the result have to do with the formula $\begin{aligned} V = \frac{4}{3} π r^{3} \end{aligned}$ ?
::将等式 r=a 以矩形形式显示, 然后找到 X 轴从 ~a 到 a 周围的变异量。结果与公式 V= 43 r 有关吗 ?

Put the equation $\begin{aligned} r = a \end{aligned}$ into rectangular form and then find the volume of its revolution around the $\begin{aligned} y \end{aligned}$ -axis from $\begin{aligned} - a \end{aligned}$ to $\begin{aligned} a \end{aligned}$ . How does your answer compare to #4? Explain.
::将等式 r=a 以矩形形式显示, 然后在 Y 轴从 ~a 到 a 周围找到它的革命量。您的回答与 # 4 相比如何? 请解释。

For #6-8, consider the equation $\begin{aligned} r = 6 \sin θ \end{aligned}$ .
::对于#6-8,考虑方程 r=6sin。

Put the equation into rectangular form.
::将方程式以矩形形式放入方形。

If you were to revolve the curve around the $\begin{aligned} y \end{aligned}$ -axis from $\begin{aligned} y = 0 \end{aligned}$ to $\begin{aligned} y = 3 \end{aligned}$ , what type of solid would you create?
::如果你绕Y轴旋转从y=0到y=3的曲线你会创造什么样的固体?

Find the volume of the revolution described in #7.
::寻找七号楼所描述的革命规模。

For #9-11, consider the equation $\begin{aligned} r = 10 \cos θ \end{aligned}$ .
::9-11,考虑一下方程 r=10cos。

Put the equation into rectangular form.
::将方程式以矩形形式放入方形。

If you were to revolve the curve around the $\begin{aligned} x \end{aligned}$ -axis from $\begin{aligned} x = 0 \end{aligned}$ to $\begin{aligned} x = 10 \end{aligned}$ , what type of solid would you create?
::如果您在 x=0 至 x=10 的 X 轴周围旋转曲线, 你会创建哪种类型的固态 ?

Find the volume of the revolution described in #10.
::寻找10号中描述的革命的量。

For #12-15, consider the equation $\begin{aligned} r = \frac{4}{\sin θ + \cos θ} \end{aligned}$ .
::12-15,考虑公式 r=4sincos。

Put the equation into rectangular form.
::将方程式以矩形形式放入方形。

If you were to revolve the curve around the $\begin{aligned} x \end{aligned}$ -axis from $\begin{aligned} x = 0 \end{aligned}$ to $\begin{aligned} x = 8 \end{aligned}$ , what type of solid would you create?
::如果您在 x=0 到 x=8 的 X 轴周围旋转曲线, 你会创建哪种类型的固态 ?

Find the volume of the revolution described in #13.
::寻找第13号所描述的革命规模。

Use the geometric formula for the volume of a cone $\begin{aligned} (V = \frac{π r^{2} h}{3}) \end{aligned}$ to find the volume of the solid described in #13. How does this answer compare to your answer to #14?
::使用锥体体体积的几何公式 (Vr2h3) 查找 #13 中所描述的固体体积。这个答案与您对 # 14 的回答相比如何 ?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

极表和微积分:革命的量

Volume of Revolution Using Polar Forms ::使用极地形式的革命量

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Volume of Revolution Using Polar Forms
::使用极地形式的革命量

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)