2.9 解决绝对值

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 解决绝对值

  Collapse Expand

  解决绝对值

  播放段落

  The tolerance for shearing a piece of sheet metal 0.25 of an inch thick is 0.1 inch. If the machine operator does not stay within 0.01 inch, the sheet metal will break. ¹ What is the range of values that the machine operator can shear at? 
  ::如果机器操作员不停留在0.01英寸之内,那么金属板就会断裂。 1 机器操作员能够剪切的数值范围是多少?

  播放段落

  We can consider this problem in terms of distance—the distance from 0.25 on the number line. In this section, we discuss how to do this. 
  ::我们可以从距离——数字线上从0.25到0.25的距离——的角度来考虑这个问题,在本节中,我们讨论如何做到这一点。

  

    

  播放段落

  Absolute Value
  ::绝对值

  播放段落

  Absolute value is the distance of a number from zero on the number line. Since it measures distance, it is always a positive number or zero. Absolute value is denoted with two vertical lines or bars as  $\begin{array}{r}|x|\end{array}$ .
  ::绝对值是数字线上数字从零到零的距离。 由于测量距离, 绝对值总是正数或零。 绝对值用两条垂直线或条表示为 x 。

  

  播放段落

  Some examples of absolute values are below.
  ::下面是绝对值的一些例子。

  $$\begin{array}{rlrlrlrlr}|4|=4& & |-3|=3& & |0|=0& & |-2.07|=2.07& & |\pi |=\pi \end{array}$$

  播放段落

  We can use absolute value to determine the distance between any two points on the number line , say  $\begin{array}{r}a\end{array}$  and  $\begin{array}{r}b\end{array}$ , by taking the absolute value of the their difference , that is,  $\begin{array}{r}|b-a|.\end{array}$  For example, say we want to find the distance between -3 and 4. That would be  $\begin{array}{r}|(-3)-4|=|-7|=7\end{array}$  or, since the order does not matter,  $\begin{array}{r}|4-(-3)|=|7|=7\end{array}$ . 
  ::我们可以使用绝对值来确定数字线上任何两个点之间的距离,例如a和b,通过使用其差数的绝对值,即b-a。例如,我们想找到-3和4之间的距离,即(-3)-477,或者,由于顺序无关紧要,4-(-3)(7)。

  播放段落

    Absolute Value and Distance Between Points on the Number Line
  ::数字线上的绝对值和距离点之间的绝对值和距离

  播放段落

  Absolute value is the distance between a number and zero on the number line. In general,
  ::绝对值是数字行数与零之间的距离。一般而言,

  播放段落

  $$\begin{array}{r}|a|=\{\begin{array}{l}a\text{if}a\ge 0\\ -a\text{if}a<0\end{array}\end{array}$$

  The distance between two numbers on the number line is
  ::数字线上两个数字之间的距离是

  播放段落

  $$\begin{array}{r}|b-a|\end{array}$$

  
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

  播放段落

  As we consider absolute value equations in this section and absolute value inequalities in the next section, we are going to want to keep the idea of absolute value measuring distance in mind. Let's see how this way of thinking works for absolute value equations. 
  ::当我们在本节中考虑绝对值方程式和下一节中考虑绝对值不平等时,我们将希望牢记测量距离的绝对值概念。让我们看看这种思维方式如何适用于绝对值方程式。

  播放段落

  Solving Absolute Value Equations
  ::解决绝对值

  播放段落

  Example 1
  ::例1

  播放段落

  Solve  $\begin{array}{r}|x|=4.\end{array}$
  ::解决4号房

  播放段落

  Solution:  As with linear equations and inequalities, solutions to absolute value equations are numbers that make the statement true. So, we are looking for a number or numbers that are 4 units from 0 on the number line.
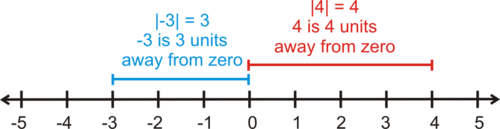
  ::解答: 和线性方程式和不平等一样, 绝对值方程式的解决方案是使声明真实的数字。 因此, 我们正在寻找数字线上从 0 到 0 的4 个数字或数字 。

  播放段落

  Let's think about this equation graphically. One option is  $\begin{array}{r}x=4\end{array}$  since 4 is 4 units from 0 on the number line. 
  ::让我们用图形来思考这个方程式。 一个选项是 x=4, 因为数字线上的 4 是 0 的 4 个单位 。

  

  播放段落

  But we can also go 4 units to the left of 0 on the number line, and get  $\begin{array}{r}x=-4.\end{array}$
  ::但我们也可以在数字线上向左0点的左侧走4个单位, 并获得 x4 。

  

  播放段落

  There are two solutions:  $\begin{array}{r}x=4\text{and}x=-4.\end{array}$
  ::有两个解决方案: x=4andx4。

  播放段落

  Another way to approach this problem is algebraically. As we have seen above,  $\begin{array}{r}x\end{array}$ can be two values—what happens when you go 4 units to the right and what happens when you go 4 units to the left. Algebraically, we have
  ::解决这一问题的另一种方法是代数法。正如我们在上面所看到的那样,x可以是两个值——当你向右走4个单位时会发生什么,向左走4个单位时会发生什么。代数法上,我们有2个值——当你向右走4个单位时会发生什么,向左走4个单位时会发生什么。

  播放段落

  $$\begin{array}{rl}& |x|=4\\ & \swarrow \searrow \\ x=4& x=-4\\ \\ \text{solution from going 4 units to the right of 0}& \text{solution from going 4 units to the left of 0}\end{array}$$

  
  ::x44444 溶液从4个单位到0左边0个单位向右0溶液

  播放段落

  Notice we took the  $\begin{array}{r}x\end{array}$  out of the absolute value bars and set it equal to 4 to represent moving to the right 4 units and we set it equal to -4 to represent moving to the left 4 units. 
  ::注意我们从绝对值栏中取出x, 设定为等于 4 表示向右移动 4 个单位, 我们设定为 - 4 表示向左移动 4 个单位 。

  播放段落

  by CK-12 demonstrates how to solve absolute value equations.  
  ::通过 CK-12 演示如何解析绝对值方程式 。

   

  播放段落

  Example 2 
  ::例2

  播放段落

  Solve $\begin{array}{r}|x-3|=2\end{array}$ .
  ::解决 _x - 3 _ 2 。

  播放段落

  Solution:  Again, let's think about this equation in terms of distance. What this equation says is that the distance between a number and 3 is 2 units. If we solve this graphically, we can start at the number we know, 3 and count 2 units in each direction. 
  ::解答: 再说一遍, 让我们从距离的角度来考虑这个方程式。 这个方程式说的是, 数字和3之间的距离是 2 个单位。 如果我们用图形解答这个, 我们可以从已知的数字开始, 3 个单位, 每个方向计数 2 个单位 。

  

  播放段落

  The solutions are  $\begin{array}{r}x=1\end{array}$  and  $\begin{array}{r}x=5\end{array}$ . Algebraically,
  ::溶液为 x=1 和 x=5. 代数,

  播放段落

  $$\begin{array}{rl}|x-& 3|=2\\ \swarrow & \searrow \\ x-3=2& x-3=-2\\ \underset{\_}{+3+3}& \underset{\_}{+3+3}\\ x=5& x=1\\ \\ \text{solution 2 units to the right of 3}& \text{solution 2 units to the left of 3}\end{array}$$

  
  ::+3+3+3+3+3_x=5x=1 解析2 单位位于3个解答 2 单位向左3个左侧的右侧

  播放段落

  To check the solutions, substitute  each value into the equation.
  ::要检查解决方案, 请在方程中替换每个值 。

  播放段落

  $$\begin{array}{rl}& x=1:|1-3|=|-2|=2\\ \\ & x=5:|5-3|=|2|=2\end{array}$$

  
  ::x=1: @% 1 - 3 @% 2 @% 2x=5: @% 5 - 3 @ 2# 2# 2

  播放段落

  Example 3
  ::例3

  播放段落

  A machine operator wants to stay within 0.1 inch of 0.25 inch with her cuts so that the sheet metal she is working with does not break. To find the maximum and minimum values of this range, we can say that the distance between a number and 0.25 is 0.1 or  $\begin{array}{r}|x-0.25|=0.1\end{array}$ . 
  ::一个机器操作员想在0.1英寸以内停留在0.25英寸的切口内,这样她所操作的金属板就不会断裂。要找到这个范围的最大值和最小值,我们可以说,数字和0.25之间的距离是0.1或x-0.250.1。

  播放段落

  Solution:  
  ::解决方案 :

  播放段落

  $$\begin{array}{rl}|x-& 0.25|=0.1\\ \swarrow & \searrow \\ x-0.25=0.1& x-0.25=-0.1\\ \underset{\_}{+0.25+0.25}& \underset{\_}{+0.25+0.25}\\ x=0.35& x=0.15\end{array}$$

  
  ::X-0.250.1x-0.25=0.1x-0.250.1+0.25+0.25_+0.25+0.25+0.25_x=0.35x=0.15

  播放段落

  So the minimum cut that a machine operator can make is 0.15 inch and the maximum is 0.35 inch.
  ::机器操作员能做的最小切口是0.15英寸 最大切口是0.35英寸

  播放段落

  Example 4
  ::例4

  播放段落

  Solve  $\begin{array}{r}|x+4|=1.\end{array}$
  ::解决 # x+4 # 1 。

  播放段落

  Solution:  Since the distance between two numbers on the number line is found by subtraction , we need to change  $\begin{array}{r}|x+4|\end{array}$  to an equivalent expression with subtraction. We can do that by subtracting the opposite (or as some like to remember it "keep, change, change"). We keep the sign of the first term , change the operation to subtraction, and change the sign of the second number from positive to negative: $\begin{array}{r}|x+4|=|x-(-4)|\end{array}$ .
  ::解答 : 由于数字线上两个数字之间的距离是通过减法找到的, 我们需要用减法将 x+4 改为一个等值的表达式 。 我们可以通过减去相反的表达式( 或者有些人喜欢记住它“ 保持、 更改、 更改 ” ) 来做到这一点。 我们保留第一个术语的符号, 将操作改为减法, 并将第二个数字的符号从正数改为负数 :\\ x+4x- (- 4)\\\\ \ \ \ \ = 。

  播放段落

  Now, we can consider this graphically. Our starting point is -4 and we consider solutions 1 unit to the right and 1 unit to the left. 
  ::现在,我们可以用图形来看待这一点。我们的起点是 - 4,我们考虑右边1个单位和左边1个单位的解决方案。

  

  播放段落

  From the image above, we see that  $\begin{array}{r}x=-5\end{array}$  and  $\begin{array}{r}x=-3\end{array}$ .
  ::从上方的图像中,我们看到 x5 和 x3 。

  播放段落

  If we want to do this algebraically, we set up two linear equations without the absolute value bars where  $\begin{array}{r}x+4\end{array}$  is equal to 1 or -1.
  ::如果我们想要进行这个代数, 我们设置两个线性方程, 没有绝对值条, x+4 等于 1 或 - 1 。

  播放段落

  $$\begin{array}{rl}|x+& 4|=1\\ \swarrow & \searrow \\ x+4=1& x+4=-1\\ \underset{\_}{-4-4}& \underset{\_}{-4-4}\\ x=-3& x=-5\end{array}$$

  Checking our solutions, we have 
  ::X+4+4+1x+4=1x+4*1 -4 -4 -4 -4 -4 -4

  播放段落

  $$\begin{array}{rl}& x=-3:|-3+4|=|1|=1\\ \\ & x=-5:|-5+4|=|-1|=1\end{array}$$

  
  ::=================================================================================================================================================== =========================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  by CK-12 demonstrates how to solve absolute value equations and interpret their solutions. 
  ::用 CK-12 演示如何解析绝对值方程式并解释其解决方案。

    

  播放段落

  Example 5
  ::例5

  播放段落

  Solve $\begin{array}{r}|\frac{2}{3}x-5|=17\end{array}$ .
  ::解决23x517

  播放段落

  Solution:  Sometimes, it is easier to consider the equation algebraically. What is inside the absolute value is equal to 17 or -17.
  ::解答: 有时, 比较容易考虑方程式代数。 绝对值内含的值等于 17 或 - 17 。

  播放段落

  $$\begin{array}{rl}|\frac{2}{3}x-& 5|=17\\ \swarrow & \searrow \\ \frac{2}{3}x-5=17& \frac{2}{3}x-5=-17\\ \frac{2}{3}x=22& \frac{2}{3}x=-12\\ x=22\times \frac{3}{2}& x=-12\times \frac{3}{2}\\ x=33& x=-18\end{array}$$

  
  ::*% 23x- 5* 17* 23x- 5= 1723x- 5 * 17 23x= 22 23x * 12 x 22x 32x * 12x 32 x = 33 x 18

  播放段落

  To check, substitute in the solutions:
  ::在解决方案中检查, 替换 :

  $$\begin{array}{rl}|\frac{2}{3}(33)-5|=17& |\frac{2}{3}(-18)-5|=17\\ |22-5|=17& |-12-5|=17\\ |17|=17& |-17|=17\\ 17=17& 17=17\end{array}$$

  播放段落

  Example 6
  ::例6

  播放段落

  Solve $\begin{array}{r}|6x-11|+2=41.\end{array}$
  ::解决 6x- 11}2=41

  播放段落

  Solution:  Before we can split this into two possibilities, we first have to isolate the absolute value term. 
  ::解决办法:在将这一方法分成两种可能性之前,我们首先必须分离绝对值术语。

  播放段落

  $$\begin{array}{r}|6x-11|+2=41\\ \underset{\_}{-2-2}\\ |6x-11|=39\end{array}$$

  
  ::6x-11_2=41-2-2_2_6x-11_39

  播放段落

  Now that the absolute value term is isolated, we can proceed as before.  
  ::既然绝对值是孤立的,我们可以像以前一样继续前进。

  播放段落

  $$\begin{array}{rl}|6x-& 11|=39\\ \swarrow & \searrow \\ 6x-11=39& 6x-11=-39\\ 6x=50& 6x=-28\\ x=\frac{50}{6}& x=-\frac{28}{6}\\ x=\frac{25}{3}& x=-\frac{14}{3}\end{array}$$

  
  ::6x- 11396x- 11= 396x- 1139 6x= 506 6x_ 28x= 506 x 286 x= 253 x 143

  播放段落

  We need to check both solutions.
  ::我们需要检查这两种解决办法。

  $$\begin{array}{rl}|6\left(\frac{25}{3}\right)-11|& =39|6\left(-\frac{14}{3}\right)-11|=39\\ |50-11|& =39|-28-11|=39\\ |39|& =39|-39|=39\\ 39& =3939=39\end{array}$$

  播放段落

  by CK-12 demonstrates how to solve absolute value equations.  
  ::通过 CK-12 演示如何解析绝对值方程式 。

    

  播放段落

  Special Cases
  ::特殊情况

  播放段落

  It is not necessarily the case that there are always two possibilities when you solve an absolute value equation. Let's consider some examples. 
  ::在解决绝对值方程式时,不一定总是有两种可能性。让我们来举几个例子。

  播放段落

  Example 7
  ::例7

  播放段落

  Solve  $\begin{array}{r}|\frac{1}{2}x+3|=0.\end{array}$
  ::解决 # 12x+3+% 0 。

  播放段落

  Solution:  We can break this up into two possibilities. 
  ::解决办法:我们可以把这个问题分成两种可能性。

  播放段落

  $$\begin{array}{rl}|\frac{1}{2}x+& 3|=0\\ \swarrow & \searrow \\ \frac{1}{2}x+3=0& \frac{1}{2}x+3=-0=0\end{array}$$

  
  ::==012x+3=012x+3=012x+3=0

  播放段落

  Our two possibilities gave us the same linear equation . We only need to solve it once.
  ::我们的两种可能性给了我们相同的线性方程 我们只需要解决一次

  播放段落

  $$\begin{array}{rl}\frac{1}{2}x& +\cancel{3}=0\\ & -\cancel{3}-3\\ & \frac{1}{2}x=-3\\ \cancel{2}\cdot & \frac{1}{\cancel{2}}x=2\cdot -3\\ & x=-6\end{array}$$

  Checking our solution: $\begin{array}{r}|\frac{1}{2}(-6)+3|=|-3+3|=|0|=0.\end{array}$
  ::12+3=0 - 3 - 312x3212x=23x 6 检查我们的解决方案: @12(-6)+3+3+3+30@0。

  播放段落

  Example 8 
  ::例8

  播放段落

  Solve  $\begin{array}{r}|5x-2|=-7.\end{array}$
  ::解决% 5x- 2@ 7 。

  播放段落

  Solution: Before breaking this up into two possibilities, let's think first about what this equation says—"the absolute value of  $\begin{array}{r}5x-2\end{array}$  is equal to -7." Since absolute value measures distance and distance is positive or zero, this is impossible. Therefore , there are no solutions. 
  ::解决方案 : 在将它分成两种可能性之前, 让我们先考虑这个方程 : “ 5x-2 的绝对值等于 - 7 ” 。 由于绝对值测量距离和距离是正的或零的, 这是不可能的。 因此, 没有解决方案 。

  播放段落

  by CK-12 demonstrates how to determine if an absolute value equation has no solutions.  
  ::CK-12表明如何确定绝对值方程式是否没有解决办法。

    

  播放段落

    How to Solve an Absolute Value Equation With Desmos
  ::如何用去摩斯解决绝对值平分

  播放段落

  Enter each side of the equation into Desmos as a function in the form y=____. Then find any values of x where the two graphs intersect.
  ::将方程式的每个侧面输入 Desmos 中,作为y 的函数。然后在两个图形交叉处找到 x 的任何值。

  播放段落

  Consider  $\begin{array}{r}|x-2|=4.\end{array}$
  ::考虑一下x -2 -4

  播放段落
  1. Graph  $\begin{array}{r}y=|x-2|\end{array}$
     ::圖表 yx-2
  播放段落
  2. The two graphs intersect when  $\begin{array}{r}x=-2\end{array}$  and when $\begin{array}{r}x=6\end{array}$ . Those are the solutions.
     ::当 x2 和 x=6 时,两个图形相交。 这就是解决方案。

  

  播放段落

   How To Solve an Absolute Value Equation With a TI-83/84
  ::如何用TI-83/84解决绝对值赤道

  播放段落
  1. Enter each side of the equation into the TI-83/84 as a function using the \fbox{Y=} button. To get to absolute value, press \fbox{MATH} and then arrow over to NUM. Absolute value is the first choice under the NUM menu. Make sure to put the expression you are taking the absolute value of inside " data-term="Parentheses" role="term" tabindex="0"> parentheses .
     ::在 TI- 83/84 中输入方程式的每边, 以 TI- 83/84 作为函数, 使用\fbox{Y} 按钮。 要达到绝对值, 请按\fbox{ MATH} 键, 然后向NUM 箭头键。 绝对值是 NUM 菜单下的第一个选择。 一定要将您在括号内的绝对值设置为表达式 。
  播放段落
  2. Press \fbox{GRAPH}.
     ::新闻\fbox{GRAPH}。
  播放段落
  3. Find the point of intersection : \fbox{2nd} \longrightarrow \fbox{CALC} and then choose option 5.
     ::查找交叉点 :\fbox{2nd}\ longrightrowr\fbox{CALC} 然后选择选项 5。

  播放段落

  by ProfThacker demonstrates how to solve an absolute value equation using a TI-83/84.  
  ::教授Thoacker展示了如何使用TI-83/84解决绝对值方程式。

   

  播放段落

  Summary
  ::摘要

  播放段落
  • Absolute value is the distance from 0 on the number line.
    ::绝对值是数字线上 0 的距离。
  播放段落
  • The distance between two numbers on the number line is  $\begin{array}{r}|b-a|\end{array}$ . 
    ::数字线上两个数字之间的距离是 b-a 。
  播放段落
  • To solve equations, remove the absolute value bars and consider a positive possibility (counting units to the right) and a negative possibility (counting units to the left).
    ::解决方程式,删除绝对值条,考虑积极的可能性(向右计数单位)和消极的可能性(向左计数单位)。

  播放段落

  Review
  ::回顾

  播放段落

  Solve the following absolute value equations.
  ::解决以下绝对值方程式。

  播放段落
  1.   $\begin{array}{r}|x+3|=8\end{array}$
     ::X+38
  播放段落
  2.   $\begin{array}{r}|2x|=9\end{array}$  
     ::2x% 9
  播放段落
  3.   $\begin{array}{r}|2x+15|=3\end{array}$
     ::2x+153
  播放段落
  4.   $\begin{array}{r}|\frac{1}{3}x-5|=2\end{array}$
     ::13x-52
  播放段落
  5.   $\begin{array}{r}|\frac{x}{6}+2|-2=5\end{array}$
     ::X6+22=5
  播放段落
  6.   $\begin{array}{r}|7x-12|=23\end{array}$
     ::7x-1223
  播放段落
  7.   $\begin{array}{r}|\frac{3}{5}x|-1.3=11\end{array}$
     ::35x1.3=11
  播放段落
  8.   $\begin{array}{r}|4x-15|+1=18\end{array}$
     ::4x -151=18
  播放段落
  9.   $\begin{array}{r}|-3x+20|=35\end{array}$
     ::3x20+35
  播放段落
  10.   $\begin{array}{r}|12x-18|=0\end{array}$
      ::12x-180

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. The average temperature in January is 32 degrees and varies by 3 degrees. What is the coldest temperature?
  ::1. 1月的平均温度为32度,变化3度,最寒冷的温度是多少?

  播放段落

  2. Your car averages 23 miles per gallon in the city. The actual mileage varies from the average by 4 miles per gallon. What is the best mileage your car can get?
  ::2. 您的汽车在城市中平均每加仑23英里,实际里程与平均每加仑4英里不同。您汽车的里程是多少?

  播放段落

  3. To determine the height of skeletal remains, archaeologists use the equation $\begin{array}{r}H=2.26f+66.4\end{array}$ , where H is the height in centimeters and f is the length of the skeleton's femur (also in cm). The equation has a margin of error of $\begin{array}{r}\pm 3.42\end{array}$  cm. Dr. Jordan found a skeletal femur that is 46.8 cm. Determine the greatest height and the least height of this person.
  ::3. 为确定骨骼遗骸的高度,考古学家使用H=2.26f+66.4等式,其中H为厘米高度,f为骨骼股骨长度(亦以厘米计),方程式误差幅度为+3.42厘米。约旦医生发现一个骨骼股骨46.8厘米。确定此人的最大高度和最小高度。

  播放段落

  4. Solve  $\begin{array}{r}|2x-3|=|x+\frac{1}{2}|\end{array}$  . (HINT: Treat one side as you would the number and create two possibilities—one where you just remove the bars and another where you negate one side. Consider how this would be true with numbers — either the numbers are equal or the numbers are opposites).
  ::4. 解决 #% 2x- 3x+12 。 (HINT: 将数字当做数字来看待, 并创造两种可能性—— 一种是删除栏杆,另一种是否定栏杆, 另一种是否定栏杆。 想想数字是真实的, 数字是相等的, 或数字是相反的) 。

  播放段落

  5. Solve $\begin{array}{r}|x-2|=|x+4|\end{array}$ .
  ::5. 解决 x-2x+4。

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see the Appendix. 
  ::请参看附录。

  播放段落

  PLIX
  ::PLIX

  播放段落

  Try this interactive that reinforces the concepts explored in this section:
  ::尝试这一互动,强化本节所探讨的概念:

  播放段落

  References
  ::参考参考资料

  播放段落

  1. “Shearing (manufacturing),” last updated January 21, 2017, .
  ::1. " 演唱(制作) " ,最近一次更新是2017年1月21日。