4.2 等式体系类型

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节各种类型同种物的体系

  折叠 展开

  各种类型同种物的体系

  The graph below is an example of a system of equations . These curves model the populations in each of the continents and the world over time starting in 1950 ¹ . In what ways can we compare these models? We will learn some terminology in this section to help us do that.

  

  播放段落

  What Is a System of Equations? 
  ::什么是等式体系?

  播放段落

     System of Equations
  ::赤道体系

  播放段落

  A system of equations is a group of equations that we consider together at one time.
  ::方程式系统是一组我们同时一起考虑的方程式。

  播放段落

  A solution to a system of equations is a point or a set of points that makes all equations true.
  ::方程体系的解决方案是将所有方程都变为真实的点或一组点。

  播放段落

  Example 1
  ::例1

  播放段落

  Determine whether (5, -9) is a solution to the following system.
  ::确定(5,9)是否是以下系统的解决办法。

  播放段落

  $$\begin{array}{rl}x+y& =-4\\ x-y& =4\end{array}$$

  
  ::xy+4x-y=4

  播放段落

  Solution: We substitute 5 for x and -9 for y .
  ::解决办法:我们用x和-9代替y。

  播放段落

  $$\begin{array}{r}5+-9=-4⟶-4=-4\\ \\ 5-(-9)=4⟶14\ne 4\end{array}$$

  Since (5,-9) is only a solution to the first equation , it is not a solution to the system.
  ::因为(5,9)只是第一个方程式的解决方案,

  播放段落

  Example 2
  ::例2

  播放段落

  According to the graph in the introduction, when did Europe and Africa have the same population?
  ::根据导言中的图表,欧洲和非洲何时拥有同样的人口?

  播放段落

  Solution: We only need to focus on the Europe curve and the Africa curve for this example. Graphs are pictures of all of the solutions to an equation. To find a solution to a system, we want a point that is on both curves. It appears that about (1995, 750) is a point on both curves. That is the solution to this system. Can you find another solution to a system on this graph?
  ::解决方案 : 我们只需要关注欧洲曲线和非洲曲线。 图表是方程式所有解决方案的图片。 要找到一个系统的解决方案, 我们想要两个曲线上都有一个点。 似乎大约(1995, 750) 是两个曲线上的一个点。 这是这个系统的解决办法 。 您能否为这个图形上的系统找到另一个解决方案 ?

  播放段落

  by CK-12 demonstrates how to determine the nature of the solutions to a system of equations.
  ::CK-12表明如何确定方程系统解决办法的性质。

  播放段落

  Consistent and Inconsistent Systems 
  ::统一和不一致的系统

  播放段落

  One way to categorize a system of equations is by whether or not there is a solution at all.
  ::将一个方程系统分类的一种方法是,是否找到解决办法。

  播放段落

      Consistent or Inconsistent
  ::不一致或不一致

  播放段落

  A system that has no solution is inconsistent .
  ::一个没有解决办法的制度是不一致的。

  播放段落

  Consistent systems are systems which have at least one solution.
  ::统一的系统是至少有一种解决办法的系统。

  播放段落

  Example 3
  ::例3

  播放段落

  
  Is the following system consistent or inconsistent?
  ::以下系统是否一致或不一致?

  播放段落

  $$\begin{array}{r}y=4x-22\\ 2x+3y=4\end{array}$$

  Solution: Graphing the system on the same set of axes, we have
  ::y=4x-222x+3y=4 溶解度: 在同一组轴上绘制系统图

  

  播放段落

  The two lines intersect at (5, -2). Since there is a solution, this system is consistent.
  ::两条线在(5,2)处交叉,因为有解决办法,所以这个系统是一贯的。

  播放段落

  Example 4
  ::例4

  播放段落

  Is the following system consistent or inconsistent?
  ::以下系统是否一致或不一致?

  播放段落

  $$\begin{array}{rl}y& =2x-5\\ y& =2x+4\end{array}$$

  
  ::y=2x-5y=2x+4 y=2x-5y=2x+4

  播放段落

  Solution: In the graph below, we can see the lines are parallel lines and never intersect. Therefore , there is no solution, so this system is inconsistent. Also, note we can see from the equations that both lines have the same but different $\begin{array}{r}y-\end{array}$ intercepts .
  ::解决方案: 在下图中, 我们可以看到线条是平行的线条, 并且从不交叉。 因此, 没有解决方案, 因此这个系统是不一致的 。 另外, 注意从公式中可以看到, 这两条线都有相同但不同的 y- inter 。

  

  播放段落

  by CK-12 demonstrates how to classify a system as either consistent or inconsistent given the graph of the system.
  ::CK-12表明,根据系统图,如何将系统分类为一致或不一致。

  播放段落

  Independent or Dependent
  ::独立或依赖

  播放段落

  Another way to describe a system of equations.
  
  ::另一种描述方程式系统的方式。

  播放段落

      Independent or Dependent
  ::独立或依赖

  播放段落

  If a  system of equations has distinct graphs, then it is independent .
  ::如果一个方程式系统有不同的图形,那么它是独立的。

  播放段落

  If the system of equation has graphs that coincide at all points, then it is dependent .
  ::如果方程式系统中的图表在所有点都吻合,则取决于该方程式。

  播放段落

  Example 5
  ::例5

  播放段落

  Is the system of equations below independent or dependent?
  
  ::等式系统是否在独立或依赖之下?

  播放段落

  $$\begin{array}{r}-2x+5y=11\\ 3x+4y=-5\end{array}$$

  Solution: Graphing the lines on the same set of axes, we have
  
  ::- 2x+5y=113x+4y=113x+4y=5 解决方案:在同一组轴上绘制线条图,我们有

  

  播放段落

  A solution to a system of equations is a point or points on both graphs. Here the point (-3,1) is on both graphs. These two graphs are distinct , so this system of equations is independent. 
  
  ::方程式系统的解决方案是两个图形的点或点。 这里的点( 3, 1) 位于两个图形上。 这两个图形是不同的, 因此这个方程式系统是独立的 。

  播放段落

  Example 6
  ::例6

  播放段落

  Is the system of equations below independent or dependent?
  ::等式系统是否在独立或依赖之下?

  播放段落

  $$\begin{array}{rl}2x-3y& =6\\ -4x+6y& =-12\end{array}$$

  
  ::2 - 3y=6-4x+6y12

  播放段落

  Solution: I n this example both lines have the same slope and y- intercept . This is more apparent when the equations are written in slope intercept form :
  ::解答 : 在此示例中, 两条线的斜度和 y 间距相同。 当方程式以斜度截击形式写成时, 这一点更明显 :

  播放段落

  $$\begin{array}{r}y=\frac{2}{3}x-2\text{and}y=\frac{2}{3}x-2\end{array}$$

  
  ::y=23x-2和y=23x-2

  播放段落

  Graphing the two lines on the same set of axes, we have:
  ::在同一组轴上绘制两条线,我们有:

  

  播放段落

  When we graph them, they are one line, we say that they  coincide , meaning they have all points in common or an infinite number of solutions in common. So, this system is dependent. 
  ::当我们绘制它们时,它们只是一行,我们说它们同时存在,意思是它们具有所有共同点或无限数的解决方案的共同点。因此,这个系统是相互依存的。

  播放段落

  We can also classify systems without graphing by comparing the slopes of the lines and sometimes their y -intercepts.
  ::我们还可以通过比较线的斜坡,有时是它们的 Y 截面,对系统进行分类,而不必绘制图表。

  播放段落

  Example 7
  ::例7

  播放段落

  Classify the following systems as consistent, inconsistent, independent or dependent.
  ::将下列系统归类为一致、不一致、独立或依赖性的系统。

  播放段落

  a.

  $$\begin{array}{rl}5x-y& =15\\ x+5y& =15\end{array}$$

  
  ::a. 5x-y=15x+5y=15

  播放段落

  b.

  $$\begin{array}{rl}9x-12y& =-24\\ -3x+4y& =8\end{array}$$

  
  ::b. 9x-12y24-3x+4y=8

  播放段落

  c.

  $$\begin{array}{rl}6x+8y& =12\\ -3x-4y& =10\end{array}$$

  
  ::c. 6x+8y=12-3x-4y=10

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  a. The first step is to rearrange both equations into slope-intercept form so that we can compare these attributes.
  ::a. 第一步是将两个方程式重新排列为斜坡界面形式,以便我们可以比较这些属性。

  播放段落

  $$\begin{array}{rl}5x-y& =15\to y=5x-15\\ x+5y& =15\to y=-\frac{1}{5}x+3\end{array}$$

  
  ::5-y=15-y=5x-15x+5y=15-y=15-y=15x+3

  播放段落

  The slopes are not the same so the lines are neither parallel nor coincident . Therefore, the lines must intersect in one point. The system is consistent and independent.
  ::斜坡不同, 所以线条既不平行也不巧合。 因此, 线条必须在一个点上交叉。 系统是一致和独立的 。

  播放段落

  b. Again, rearrange the equations into slope-intercept form:
  ::b. 同样,将方程式重新排列为斜坡界面:

  播放段落

  $$\begin{array}{rl}9x-12y=-24& \to y=\frac{3}{4}x+2\\ -3x+4y=8& \to y=\frac{3}{4}x+2\end{array}$$

  
  ::9 - 12y24y=34x+2 - 3x+4y=8y=34x+2

  播放段落

  Now, we can see that both the slope and the y- intercept are the same and therefore the lines are coincident. The system is consistent and dependent.
  ::现在,我们可以看到,斜坡和 Y 界面是相同的, 因此线条是同时的。 系统是一贯的, 并依附的 。

  播放段落

  c. The equations can be rewritten as follows:
  ::c. 等式可改写如下:

  播放段落

  $$\begin{array}{rl}6x+8y& =12\to y=-\frac{3}{4}x+\frac{3}{2}\\ -3x-4y& =10\to y=-\frac{3}{4}x-\frac{5}{2}\end{array}$$

  
  ::6x+8y=12y34x+32-33x-4y=10y34x-52

  播放段落

  In this system the lines have the same slope but different y- intercepts so they are parallel lines. Therefore the system is inconsistent. 
  ::在这个系统中,线条具有相同的斜坡,但有不同的 Y 界面,因此它们是平行的线条。因此,这个系统是不一致的。

  播放段落

  by MyWhyU demonstrates how to classify systems based on the number of solutions it has. 
  ::由 MyHauseU 演示如何根据已有的解决方案数量对系统进行分类。

  播放段落

  
  
  Summary
  ::摘要

  播放段落
  • 播放段落

    A system of equations is a group of equations that we consider together at one time. A solution to a system of equations is a point or a set of points that makes all equations true.
    ::方程体系是一组我们同时共同考虑的方程。 方程体系的解决方案是让所有方程都真实的点或一组点。

    
    ::方程体系是一组我们同时共同考虑的方程。 方程体系的解决方案是让所有方程都真实的点或一组点。
  播放段落
  • 播放段落

    If a  system of equations has distinct graphs, then it is independent. If the system of equations has graphs that coincide at all points, then it is dependent.
    ::如果一个方程式系统有不同的图形,那么它是独立的。如果该方程式系统有在所有点都相同的图形,那么它就取决于它。

    
    ::如果一个方程式系统有不同的图形,那么它是独立的。如果该方程式系统有在所有点都相同的图形,那么它就取决于它。
  播放段落
  • A system that has no solution is inconsistent. Consistent systems are systems which have at least one solution.
    ::一个没有解决办法的系统是不一致的,一致的系统是至少有一个解决办法的系统。

  播放段落
  • While we can determine these properties by graphing, we can also compare these properties by comparing the slopes and the y -intercepts of the lines.
    ::虽然我们可以通过图形化来确定这些属性,但我们也可以比较这些属性,比较斜坡和线的 Y 截面。

  播放段落

  Review
  ::回顾

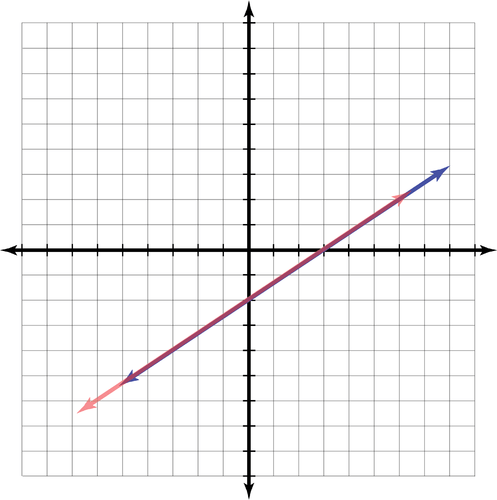
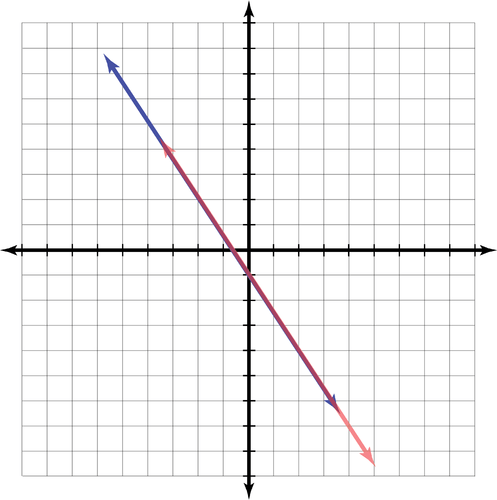
  播放段落

  Describe the systems graphed below both algebraically (consistent, inconsistent, dependent, independent) and geometrically (intersecting lines, parallel lines, coincident lines).
  ::描述在代数(一致、不一致、依赖、独立)和几何(交叉线、平行线、正对线)下图解的系统。

  1.

  

  2.

  

  3.

  

  播放段落

  Classify the following systems as consistent, inconsistent, independent or dependent. You may do this with or without graphing them. You do not need to find the unique solution if there is one.
  ::将以下系统分类为一致、不一致、独立或依赖性。您可以使用或不绘制图表的方式这样做。如果存在,您不需要找到唯一的解决方案。

  播放段落

  4.  
  $\begin{array}{r}4x-y=8\\ y=4x+3\end{array}$
  ::4. 4x-y=8y=4x+3

  播放段落

  5.
  $\begin{array}{r}5x+y=10\\ y=5x+10\end{array}$
  ::5. 5x+y=10y=5x+10

  播放段落

  6. 
  $\begin{array}{r}\begin{array}{rl}& 2x-2y=11\\ & y=x+13\end{array}\end{array}$
  ::6. 2x-2y=11y=x+13

  播放段落

  . 7. 
  $\begin{array}{r}\begin{array}{rl}& -7x+3y=-21\\ & 14x-6y=42\end{array}\end{array}$
  ::7-7x+3y2114x-6y=42

  播放段落

  . 8. 
  $\begin{array}{r}\begin{array}{rl}& y=-\frac{3}{5}x+1\\ & 3x+5y=5\end{array}\end{array}$
  ::8. y35x+13x+5y=5

  播放段落

  . 9. 
  $\begin{array}{r}\begin{array}{r}6x-y=18\\ y=\frac{1}{6}x+3\end{array}\end{array}$
  ::9.9. 6x-y=18y=16x+3

  播放段落

  10.   
  $\begin{array}{r}\begin{array}{rl}& x=2\\ & 8x+3y=-11\end{array}\end{array}$
  ::10. x=28x+3y11

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. Write your own systems with equations in standard form, $\begin{array}{r}Ax+By=C\end{array}$ . Try to make them look different even if they are the same equation.
  ::1. 用标准格式Ax+By=C的方程式书写自己的系统。 尽量使其看起来不同,即使它们相同方程式。

  播放段落

  a. Write a system which is consistent and independent.
  ::a. 编写一个前后一致和独立的系统。

  播放段落

  b. Write a system which is consistent and dependent.
  ::b. 编写一个前后一致和依赖性的系统。

  播放段落

  c. Write a system which is inconsistent.
  ::c. 编写不一致的系统。

  播放段落

  d. Write a system where the solution is (-1, 2), one line is vertical and the second is horizontal.
  ::d. 写入一个解决方案为(-1,2),一条线为垂直,第二条为水平的系统。

  播放段落

  e. Write a system where the solution is (-1, 2), one line is vertical or horizontal and the second is neither.
  ::e. 写入一个解决方案为(-1,2)的系统,其中一条线为垂直或水平线,第二条线为两条。

  播放段落

  f. Write a system where the solution is (-1, 2) and neither line is vertical nor horizontal.
  ::f. 写入一个解决办法为(-1,2)的系统,无论是垂直线还是横向线。

  播放段落

  2. Is it possible to have a system that is dependent and inconsistent? Explain. 
  ::2. 是否有可能有一个依赖性和不一致的系统?

  播放段落

  3. In the model about population growth above, is (-3,-2,500) a reasonable solution?  Let time be the independent variable and number of people the dependent variable.
  ::3. 在以上关于人口增长的模型中,(3-2,500)是否是一个合理的解决办法?让时间成为独立的变量,让人数成为依赖变量。

  播放段落

  4. Sonia  buys two apples and three bananas for $4. Muhammad buys four apples and six bananas for $8 from the same store.  Write and solve a system equations to represent this situation . Use the number of solutions to characterize the system. 
  ::4. 索尼娅以4美元购买2个苹果和3个香蕉。穆罕默德从同一家商店购买4个苹果和6个香蕉,8美元。写和解决一个系统方程式来反映这种情况。用解决方案的数目来说明这个系统的特点。

  播放段落

  5.  Peter and Nadia like to race each other. Peter can run at a speed of 5 feet per second and Nadia can run at a speed of 6 feet per second. To be a good sport, Nadia likes to give Peter a head start of 20 feet. Write and solve a system equations to represent this situation. Use the number of solutions to characterize the system. 
  ::5. Peter和Nadia喜欢相互竞争:Peter每秒可以以5英尺的速度运行,Nadia每秒可以以6英尺的速度运行。为了运动,Nadia喜欢让Peter头起20英尺。写和解决一个系统方程式来代表这种情况。使用解决方案的数量来描述系统特征。

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see the Appendix.
  ::请参看附录。

  播放段落

  References
  ::参考参考资料

  播放段落

  1. "World population," last edited on May 15, 2017, https://en.wikipedia.org/wiki/World_population.  
  ::1. "世界人口 " ,上次编辑于2017年5月15日,https://en.wikipedia.org/wiki/world_population。