8.10 赤道模型

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 二次曲线模型

  Collapse Expand

  二次曲线模型

  播放段落

  On reduced-gravity flights, airplanes fly in large parabolic arcs. Say a reduced-gravity flight flies along the path $\begin{align*}y=\text{-}0.018x^2+1.53x+0.13\end{align*}$ , where x is the time in seconds, and  y is the altitude in thousands of feet. When will the flight reach its maximum height? What is the maximum height? When will the flight land? We discuss how to analyze a quadratic model like this in this section.
  ::减重飞行时, 飞机以大型抛物弧飞行。 说减重飞行沿着 y=- 0.018x2+1.53x+0. 13 的路径飞行, x 是秒中的时间, y 是千英尺中的高度。 飞行何时会达到最高高度? 最高高度是多少? 飞行何时会降落? 我们在本节中讨论如何分析这样的四边模型 。

  

  播放段落

  Quadratic Models 
  ::二次曲线模型

  播放段落

  We consider several quadratic models in this section. Often, we are asked to maximize or minimize the model. If the parabola opens upward, the minimum point is the vertex . If the parabola opens downward, the maximum point is the vertex. 
  ::我们在本节考虑几种二次模型。 通常, 我们被要求最大化或最小化模型。 如果抛物线向上打开, 最低点是顶点。 如果抛物线向下打开, 最大点是顶点 。

  播放段落

  Example 1
  ::例1

  播放段落

  A farmer wants to fence in a rectangular grazing area next to a river. He has 800 yards of fence. What should the dimensions of the rectangular grazing area be to maximize the area? 
  ::农民想在河边的长方形放牧区围成栅栏,他有800码的栅栏。 长方形放牧区的面积应该有多大才能使面积最大化?

  播放段落

  Solution: One side of the rectangle is the length along the river. So the fence has to cover two widths and one length: the perimeter (the distance around the shape), minus the one length that is the side along the river.
  ::解答:矩形的一面是沿河的长度。所以栅栏必须覆盖两个宽度和一个长:周边(形状周围的距离)减去河边的一长。

  播放段落

  $$\begin{align*}2w+l=800\end{align*}$$
  ::2w+l=800

  播放段落

  Since $\begin{align*}A=lw\end{align*}$ , we can isolate for either $\begin{align*}l\end{align*}$  or $\begin{align*}w\end{align*}$  in the perimeter equation and substitute into the area equation.
  ::自A=lw以来,我们可以在周边方程中将l或w分离成l或w,并替换成区域方程。

  播放段落

  $$\begin{align*}2w&+l=800 \\ l&=800-2w\\ \\ A&=(800-2w)w\\ &=800w-2w^2\\ &=\text{-}2w^2+800w\end{align*}$$
  ::2w+l=800l=800-2-2wA=(800-2w)w=800-2w2=-2w2+800w

  播放段落

  This is now a quadratic model. To maximize this model, we need to find the vertex.
  ::现在这是一个二次模型。 要尽量扩大这个模型, 我们需要找到顶点 。

  播放段落

  $$\begin{align*}w&=\text{-}\frac{b}{2a}=\text{-}\frac{800}{2 \cdot \text{-}2}= 200 \\ \\ l&=800-2w=800-2(200)=800-400=400\end{align*}$$
  ::w=-b2a=-8002-2=200l=800-2w=800-2w=800-2(200)=800-400=400

  播放段落

  The width that maximizes the area is 200 yards, and the length that maximizes the area is 400 yards.      
  ::使面积最大化的宽度为200码,使面积最大化的宽度为400码。

  播放段落

  This video by James Hablin shows a similar problem.
  ::这段影片由James Hablin拍摄,

   

  播放段落

  Example 2
  ::例2

  播放段落

  A company sells a product whose demand—how many purchases will be made given a particular price, p— can be modeled by $\begin{align*}d=1,\!200-40p\end{align*}$ . What price should the company charge to maximize the revenue ? What is the maximum revenue? 
  ::一家公司销售一种产品,其需求是多少次采购将给定特定价格,而这种价格的模型是d=1200-40p。 公司应收取什么价格来最大限度地增加收入?最高收入是多少?

  播放段落

  Solution: The revenue of a company is the number of products sold times the price that the product is sold for, or  $\begin{align*}R=dp\end{align*}$ . We can express this model in terms of just the price by substituting for $\begin{align*}d\end{align*}$ .
  ::解决办法:公司的收入是销售产品的数量乘以产品售出的价格,或R=dp。我们可以用价格来表示这一模式,代之以d。

  播放段落

  $$\begin{align*}R=dp=(1,\!200-40p)p=1,\!200p-40p^2=\text{-}40p^2+1,\!200p\end{align*}$$    
  ::R=dp=(1200-40p)p=1200p-40p2=-40p2+1200p

  播放段落

  To maximize the revenue, we need to find the vertex.
  ::为了最大限度地增加收入,我们需要找到顶点。

  播放段落

  $$\begin{align*}p&=\text{-}\frac{b}{2a}=\text{-}\frac{1,\!200}{2 \cdot \text{-}40}=15 \\ \\ R&=\text{-}40(15)^2+1,\!200(15)=\text{-}9,\!000+18,\!000=9,\!000\end{align*}$$
  ::p=-b2a=-1,2002-40=15R=-40(1552)2+1200(15)=-9,000+18,000=9,000

  播放段落

  The company should charge $15 for the product to maximize the revenue of $9,000.  
  ::该公司应为产品收取15美元,以最大限度地增加9 000美元的收入。

  播放段落

  This video by Mathispower4u shows a similar problem.
  ::Mathispower4u的这段影片也呈现类似问题。

   

  播放段落

  
  Example 3
  ::例3

  播放段落

  A reduced-gravity flight flies along the path $\begin{align*}y=\text{-}0.018x^2+1.53x+0.13\end{align*}$ , where $\begin{align*}x\end{align*}$  is the time in seconds, and $\begin{align*}y\end{align*}$  is the altitude in thousands of feet. When will the flight reach its maximum height? What is the maximum height? When will the flight land?
  ::降低重力飞行沿 y =- 0.018x2+1.53x+0. 13 路径飞行, x 秒为秒, y 是千英尺的高度。 飞行何时达到最高高度? 最大高度是多少? 飞行何时着陆?

  播放段落

  Solution: To maximize this model, we need to find the vertex.
  ::解决方案: 要尽量扩大这个模型, 我们需要找到顶点 。

  播放段落

  $$\begin{align*}x&=\text{-}\frac{b}{2a}=-\frac{1.53}{2 \cdot \text{-}0.018}=42.5\\ \\ y&=\text{-}0.018(42.5)^2+1.53(42.5)+0.13=32.6\end{align*}$$
  ::x=-b2a=1.532-0.018=42.5y=-0.018(42.5)2+1.53(42.5)+0.13=32.6

  播放段落

  The flight will reach its maximum height at 42.5 seconds into the flight. The maximum altitude is 32,600 feet.
  ::飞行最高高度为42.5秒,最高高度为32 600英尺。

  播放段落

  The flight will land when the height is 0 feet, so we need to solve the quadratic equation .
  ::飞行在高度为0英尺时会降落 所以我们需要解决二次方程

  播放段落

  $$\begin{align*}x=\text{-}\frac{1.53 \pm \sqrt{(1.53)^2-4(\text{-}0.018)(0.13)}}{2(\text{-}0.018)}\\ x=\text{-}0.08 \qquad x=85.1\end{align*}$$ The flight lands after 85.1 seconds.   
  ::x=-1.53(1.532)-2-4(-0.018)(0.132(-0.018)x=-0.08x=85.1)。

  播放段落

  This video by Ella Sitkin shows a similar problem. 
  ::Ella Sitkin的这段影片也呈现类似问题。

   

  播放段落

  Summary
  ::摘要

  播放段落
  • To maximize or minimize a quadratic model, find the vertex. If the parabola opens upward, the vertex represents a minimum. If the parabola opens downward, the vertex represents a maximum. 
    ::要最大化或最小化二次模型,请找到顶点。如果抛物线向上打开,顶点代表最小值。如果抛物线向下打开,顶点代表最大值。

  播放段落

  Review
  ::回顾

  播放段落

  1. A doggy day care has 500 feet of fencing to make rectangular playpen for the dogs. What should the dimensions of the sides be to maximize the area inside the playpen?
  ::1. 养狗日托有500英尺长的栅栏,为狗做长方形弹簧,边边的尺寸应该如何,以尽量扩大弹棚内的面积?

  播放段落

  2. A property owner wants to fence off a rectangular section of her backyard around the back of her house, where one side of the rectangle is the back of the house. To fence in the other three sides, she has 80 feet of fencing. If she wants to maximize the area, will the length of the backyard fit between her property lines that are 35 feet apart?
  ::2. 房主想将后院的长方形区域围在后院的后面,而后院的一面是后院,另外三面有80英尺的栅栏,如果她想尽量扩大面积,后院的长度在35英尺的地产线之间会合吗?

  播放段落

  3. The demand equation for a product is $\begin{align*}x=300-4p\end{align*}$ . What is the maximum revenue for this product?
  ::3. 产品的需求方程式为x=300-4p。 该产品的最大收入是多少?

  播放段落

  4. A batter hits a home run into the stands that can be modeled by the equation $\begin{align*}y=\text{-}0.003x^2+1.3x+4\end{align*}$ , where is the horizontal distance and is the height (in feet) of the ball. Find the maximum height of the ball and its total distance traveled.
  ::4. 击打击击打到可模拟Y=-0.003x2+1.3x+4等式的站台的全垒打,这里是水平距离,是球的高度(脚),找到球的最大高度及其总距离。

  播放段落

  5. One leg of a right triangle is 6 feet longer than the other leg. If the hypotenuse is 50 feet, what are the dimensions of the two legs?
  ::5. 右三角的一条腿比另一条腿长6英尺,如果下限为50英尺,两条腿的尺寸是多少?

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. A container in the shape of a right circular cylinder with no top has surface area 3 ft ² . What height h and base radius r will maximize the volume of the cylinder?
  ::1. 以右圆环圆柱形形状的容器,没有顶部的表面面积为3平方英尺。 圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆圆

  播放段落

  2. a. Create an equation to model the height,  $\begin{align*}h(t)\end{align*}$ , of a roller coaster over time, t . Suppose the maximum height is 80 m, and the horizontal distance between the starting and ending point is 160 m. Also assume that the starting point was the origin (0,0).
  ::2. a. 建立一个方程,以模拟时空过山车的高度(h(t)),t. 假设最大高度为80米,起点和终点之间的水平距离为160米。还假设起点是起点(0,0)。

  播放段落

  b. Suppose you wanted your roller coaster to be steeper. More specifically, suppose you want to perform a vertical stretch by a factor of 2.
  ::b. 假设你想你的过山车更陡峭,更具体地说,假设你想以2乘以2进行垂直伸展。

  播放段落

  3. The owner of a 20-unit condominium community has found that each $50 increase in monthly rent results in one additional vacant condominium. All condominiums are rented at $400 per month. How many $50 increases in rent will produce the largest possible income for the owner?
  ::3. 共有20个单元的共有公寓社区的业主发现,每月租金每增加50美元,就会增加一个空置的共有公寓,所有共有公寓都以每月400美元的租金租用,租金增加多少50美元将给所有者带来最大的收入?

  播放段落

  4. An engineer designed a new smartphone with the goal of manufacturing as many of them as necessary to maximize profit. The engineer has the following costs: $700,000 to manufacture set-up costs, advertising, etc., and $110 to make each smartphone. Sales are expected to follow the following demand curve: $\begin{align*}\text{Unit Sales} = 70,\!000 - 200P\end{align*}$ , where P  is the price. What is the best price? How many smartphones should be  produced ?
  ::4. 一名工程师设计了一个新的智能手机,目的是制造尽可能多的智能手机,以获得最大利润;工程师有以下费用:70万美元用于制造安装费用、广告等,110美元用于制作每部智能手机;预期销售将遵循下列需求曲线:United Celse=70,000-200P,P的价格在哪里;最佳价格是多少?应生产多少智能手机?

  播放段落

  The following problems require a graphing calculator or a graphing utility, like Desmos.  Round any decimal answers to the nearest hundredth.
  ::下列问题需要一个图形计算器或图形工具, 如 Desmos 。 任何小数点后, 都会在最接近的百分百处回答 。

  播放段落

  This video by Mathispower4u will help you do quadratic regression in Desmos. 
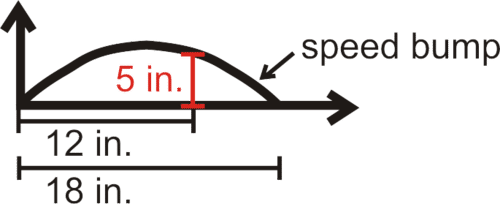
  ::这部影片由Mathispower4u拍摄,

   

  播放段落

  5. The surface of a speed bump is shaped like a parabola. Write a quadratic model for the surface of the speed bump shown.
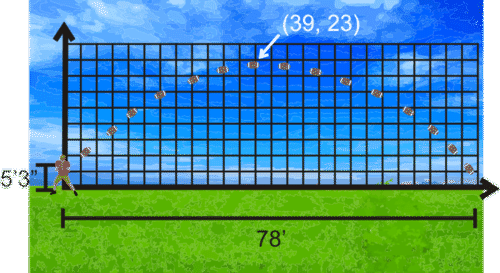
  ::5. 速度峰值表面形状像抛物线,为显示速度峰值表面写一个二次模型。

  

  播放段落

  6. You know that when a person throws a football, the path is a parabola. Using your camera, you take a long exposure picture of a friend throwing a football. A sketch of the picture is below.
  ::6. 你知道,当一个人扔足球时,这条路就是抛物线,用你的相机拍摄一个朋友扔足球的长片,照片的草图在下面。

  

  播放段落

  You put the path of the football over a grid, with the $\begin{align*}x-\end{align*}$ axis as the horizontal distance and the $\begin{align*}y-\end{align*}$ axis as the height, both in 3-foot increments. The release point, or shoulder height, of your friend is 5 ft, 3 in, and you estimate that the maximum height is 23 feet. Find the equation of the parabola.
  ::您将足球的路径放在网格上, X - 轴作为水平距离, y - 轴作为高度, 在三英尺的递增中都是如此。 您朋友的释放点或肩高是 5 英尺, 3 英寸, 您估计最高高度是 23 英尺。 找到 parbola 的方程 。

  播放段落

  7. An independent study was done linking advertising to the purchase of an object. Four hundred  households were used in the survey, and the commercial exposure was over a one-week period. See the data set below.
  ::7. 进行了一项独立研究,将广告与购买物品联系起来,在调查中使用了400户家庭,商业接触时间为一周,见下文数据。

  # of times commercial was shown, $\begin{align*}x\end{align*}$	1	7	14	21	28	35	42	49
  # of households bought item, $\begin{align*}y\end{align*}$	2	25	96	138	88	37	8	6

  播放段落

  a. Find the quadratic equation of best fit.
  ::a. 找到最适合的二次方程。

  播放段落

  b. Why do you think the amount of homes that purchased the item went down after more exposure to the commercial?
  ::b. 为什么你认为购买该物品的房屋数量在更多地接触该商业产品后下降?

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see the Appendix.  
  ::请参看附录。