9.8 在标准表格中绘制对等功能图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 标准表格中图示对等函数

  Collapse Expand

  标准表格中图示对等函数

  播放段落

  The time to empty a tank by pumping out the contents varies inversely as the rate of pumping. If the pump works at a rate of 30 gallons per hour, how much is in a tank that started with 300 gallons at 2 hours? At 5 hours? At 10 hours? 
  ::通过抽出罐装物来清空罐体的时间与抽水速度不同,与抽水速度不同。如果泵每小时工作30加仑,在2小时以300加仑为起点的罐体里有多少?5小时?10小时?

  播放段落

  Instead of having to solve three separate equations for each of these values, we can draw a graph of this situation and then read the values from the graph. I n this section, w e consider how to graph reciprocal functions in standard form .
  ::我们不用为每个数值解析三个不同的方程式, 我们就可以绘制一个图表, 然后从图表中读取数值 。 在本节中, 我们考虑如何用标准格式绘制对等函数 。

  

  播放段落

  Rational Functions in Standard Form
  ::标准表格中的理性函数

  播放段落

  A rational function is a function in the form  $\begin{array}{r}\frac{p\left(x\right)}{q\left(x\right)},\end{array}$ where $\begin{array}{r}p(x)\end{array}$ and $\begin{array}{r}q(x)\end{array}$ are and $\begin{array}{r}q(x)\ne 0\end{array}$ . The parent graph for some rational functions is $\begin{array}{r}y=\frac{1}{x}\end{array}$ . Below we have a table of values for this function.
  ::理性函数是在 p( x) q( x) 表中的函数。 p( x) 和 q( x) 是和 q( x) =% 0 。 某些理性函数的父图是 y= 1x。 下面我们有一个此函数的数值表 。

  $$\begin{array}{r}x\end{array}$$	$$\begin{array}{r}y=\frac{1}{x}\end{array}$$
  $\begin{array}{r}\text{-}4\end{array}$	$\begin{array}{r}\text{-}\frac{1}{4}\end{array}$
  $\begin{array}{r}\text{-}2\end{array}$	$\begin{array}{r}\text{-}\frac{1}{2}\end{array}$
  $\begin{array}{r}\text{-}1\end{array}$	$\begin{array}{r}\text{-}1\end{array}$
  $\begin{array}{r}\text{-}\frac{1}{2}\end{array}$	$\begin{array}{r}\text{-}2\end{array}$
  0	undefined
  $\begin{array}{r}\frac{1}{2}\end{array}$	2
  1	1
  2	$\begin{array}{r}\frac{1}{2}\end{array}$
  4	$\begin{array}{r}\frac{1}{4}\end{array}$

  播放段落

  Notice that the  y -values are reciprocals of the  x -values. Hence, this function is called the reciprocal function . The graph of the function is below. This shape is called a   hyperbola .
  ::注意 Y 值是 x 值的对等值。 因此, 此函数被称为对等函数。 此函数的图形在下面。 此形状被称为双曲线 。

  

  播放段落

  The two parts of the graph are called branches and are divided by two boundary lines called asymptotes . The two asymptotes in this case are the  x -axis and the  y -axis. For a hyperbola, the branches are always symmetrical about the point where the asymptotes intersect. In this example, they are symmetrical about the origin.
  ::图形的两部分被称为分支, 并用两个叫做 asymptotes 的边界线分隔。 这里的两小段是 X 轴和 y 轴。 对于双倍波拉来说, 树枝总是对称的, 与 asymptotes 交叉点的对称。 在此示例中, 树枝和 y- 轴对称 。

  播放段落

  If we apply the transformation rules to this parent graph, we can express  the standard form of a reciprocal  function . 
  ::如果我们将转换规则应用到此父图中, 我们可以表达对等函数的标准形式 。

  播放段落

     Standard Form of a Reciprocal  Function
  ::互惠职能标准格式

  The standard form of a reciprocal function is given by the equation $\begin{array}{r}f(x)=\frac{a}{x-h}+k\end{array}$ . 

  播放段落

  Below we consider how to graph  reciprocal functions of  the form $\begin{array}{r}f(x)=\frac{a}{x-h}+k\end{array}$ . First, we need to deal with some preliminaries. 
  ::下面我们考虑如何绘制表格f(x)=ax-h+k的对等函数。 首先,我们需要处理一些初步问题。

  播放段落

  Domain of a Rational Function
  ::逻辑函数域域域

  播放段落

  Recall that the domain of a function is the set of possible  inputs to the function. Notice in the graph of  $\begin{array}{r}y=\frac{1}{x}\end{array}$  above that when we tried to input 0, we got an undefined result. This means we need to eliminate 0 from the domain of  $\begin{array}{r}y=\frac{1}{x}\end{array}$ . In set-builder notation, we can write this as $\begin{array}{r}\{x\in \mathbb{R}|x\ne 0\},\end{array}$  or in interval notation we can write this as  $\begin{array}{r}(\text{-}\mathrm{\infty },0)\cup (0,\mathrm{\infty })\end{array}$ .
  ::回顾函数的域是该函数的一组可能的输入。 y=1x以上图中的注意, 当我们尝试输入 0 时, 我们得到了一个未定义的结果 。 这意味着我们需要从 y= 1x 的域中删除 0 。 在设置- 构建器的标记中, 我们可以将此写成 {xR x0} , 或者在间隔符号中, 我们可以将此写成 (- , 0)\\\\\\\ (0 ) 。

  播放段落

  In general, we need to be aware of the potential for domain problems when we are dealing with rational functions. Since they are fractions, we do not want the denominators to be equal to zero. To determine which values to eliminate from the domain of a rational function, set the denominator equal to zero and solve. The solutions are values that will make the denominator equal to zero and need to be eliminated from the domain.
  ::一般来说,当我们处理理性功能时,我们需要意识到领域问题的潜在可能性。 由于它们是分数, 我们不希望分数等于零。 要确定从理性函数领域消除哪些值, 将分数等于零并解决。 解决方案是使分数等于零并需要从领域消除的值。

  播放段落

  Example 1
  ::例1

  播放段落

  Determine the domain of the rational functions below. (Note: Some of these are not in standard form. We will cover these in the next section.)
  :注:其中一些不是标准格式,我们将在下一节中述及。 )

  播放段落

  a. $\begin{array}{r}y=\frac{3}{x+4}+6\end{array}$
  ::a. y=3x+4+6

  播放段落

  b. $\begin{array}{r}y=\frac{3x-1}{4x+8}\end{array}$
  ::b. y=3x-14x+8

  播放段落

  c. $\begin{array}{r}y=\frac{4}{x^2+5x+6}\end{array}$
  ::c. y=4x2+5x+6

  播放段落

  d. $\begin{array}{r}y=\frac{1}{x^2+4}\end{array}$
  ::d. y=1x2+4

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  a. When we set $\begin{array}{r}x+4=0\end{array}$ , we find $\begin{array}{r}x=\text{-}4\end{array}$ . Therefore , the domain of this function is $\begin{array}{r}\{x\in \mathbb{R}|x\ne \text{-}4\}\end{array}$ or $\begin{array}{r}\left(\text{-}\mathrm{\infty },\text{-}4\right)\cup \left(4,\mathrm{\infty }\right)\end{array}$ . 
  ::a. 当我们设定 x+4=0 时,我们发现 x=4。因此,此函数的域是 {xR {xR x* 4} 或 (-, 4) {(4, }) 。

  播放段落

  b. $\begin{array}{r}4x+8=0⟶x=\text{-}2\end{array}$ . The domain of the function is $\begin{array}{r}\{x\in \mathbb{R}|x\ne \text{-}2\}\end{array}$  or  $\begin{array}{r}(\text{-}\mathrm{\infty },\text{-}2)\cup (\text{-}2,\mathrm{\infty })\end{array}$ .
  ::b. b. 4x+8=0x=2。函数的域为 {xR {xR {x* x*-2} 或 (-,-2) (-2) 。

  播放段落

  c.

  $$\begin{array}{rl}{x}^2+5x+6& =0\\ (x+2)(x+3)& =0\\ x=\text{-}2& x=\text{-}3\\ \\ \text{dom}y& =\{x\in \mathbb{R}|x\ne \text{-}2,x\ne \text{-}3\}\\ & =(\text{-}\mathrm{\infty },\text{-}3)\cup (\text{-}3,\text{-}2)\cup (\text{-}2,\mathrm{\infty })\end{array}$$

  Be careful to include the middle interval, which is part of the solution.
  ::c. x2+5x+6=0(x+2(x+2)(x+3)=0x=2x=2x=3dom yxRxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx=2xxxxxxxxxxxx=2xxxxxxxxxx=3xxxxxxxxxxxxxxxxxx=3xxxxxxx=3=3x3xxxxxxxxx=3x3=3d y*xxxxxxxxxxxxxxxxxxxxx=3=3=3=3xxxxx3=3=3=3dxx3=3=3=3=3x3x3x3x3=3xxxxxxxx3=3=3=3dx3dxxx3=3=3=3=3=3xxxxxxxx3x3x3x3x3x3xx3x3=3=3=3=3=3=3x3dxxx3xxxxx3=3=3dx3dxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx3x3xxxx3xxxxxxx3xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx=3=3=3=3=3=3

  播放段落

  d. $\begin{array}{r}{x}^2+4=0\end{array}$  has no real solutions. Therefore, the denominator is never zero, and the domain is all real numbers.
  ::d. x2+4=0 没有真正的解决方案。 因此, 分母从不为零, 域名全部为真实数字 。

  播放段落

  Vertical Asymptotes in Standard Form
  ::标准表格中的垂直垂直单位数

  播放段落

  The vertical boundary line or asymptote is caused by the value that is the domain concern , when  $\begin{array}{r}x-h=0.\end{array}$  Around the vertical asymptote , the  y -values increase or decrease without bound. 
  ::垂直边界线或无线线线是由当 x-h=0 时的域内关注值造成的。在垂直线线上,Y值在无约束情况下增减。

  播放段落

     Vertical Asymptote in Standard Form
  ::标准表格中的垂直时数

  There will be a vertical asymptote at  $\begin{array}{r}x=h.\end{array}$

  播放段落

  Horizontal Asymptotes in Standard Form
  ::标准表格中的水平单位

  播放段落

  describe how the graph behaves for large values of $\begin{array}{r}|x|\end{array}$ . When this is true, the 1st term in standard form is a fixed number divided by a large number, which we can estimate to be zero. Then, the only term remaining is k , so the horizontal asymptote is  $\begin{array}{r}y=k\end{array}$ . This is the end behavior of a rational function. The function will be close to the horizontal line,   $\begin{array}{r}y=k.\end{array}$  
  ::描述图表对 {x}} 的大值的行为方式。 如果这是真的, 标准格式的第一个词是固定数字除以大数, 我们可以估计为零。 然后, 剩下的唯一词是 k, 所以水平的 asymptote 是 y=k。 这是理性函数的结束行为。 函数将接近水平线, y=k 。

  播放段落

     Horizontal Asymptote in Standard Form
  ::标准表格中的水平单数

  There will be a horizontal asymptote at  $\begin{array}{r}y=k\end{array}$ .

  播放段落

  Example 2
  ::例2

  播放段落

  What are the asymptotes for $\begin{array}{r}f(x)=\frac{\text{-}1}{x+6}+9\end{array}$ ? 
  ::f( x) =-1x+6+9 的小数点数是什么 ?

  播放段落

  Solution:   The asymptotes are $\begin{array}{r}x=\text{-}6\end{array}$   and   $\begin{array}{r}y=9\end{array}$ .
  ::解析度: asymptotes 是 x= 6 和 y= 9 。

  播放段落

  Graphing Rational Functions in Standard Form      
  ::在标准表格中绘制逻辑函数

  播放段落

     To Graph a Rational Function in Standard Form
  ::在标准表格中绘制一个有理函数

  播放段落

  1. Determine the domain of the function. This will also be the location of the vertical asymptote. 
  ::1. 确定函数的域,这还将是垂直零点的位置。

  播放段落

  2. Find the horizontal asymptote. 
  ::2. 寻找水平的零星状态。

  播放段落

  3. Create a table of values with some values to the right of the vertical asymptote, and some to the left of the vertical asymptote. 
  ::3. 创建一个数值表,其中含有垂直单点右侧的一些值,还有一些在垂直单点左侧的一些值。

  播放段落

  Example 3
  ::例3

  播放段落

  Graph $\begin{array}{r}f(x)=\frac{\text{-}2}{x}\end{array}$ . 
  ::图f(x)=-2x。

  播放段落

  Solution:  First, the domain is all real numbers except $\begin{array}{r}x=0\end{array}$ , so $\begin{array}{r}x=0\end{array}$  is also the vertical asymptote. The horizontal asymptote is  $\begin{array}{r}y=0\end{array}$  since there is no value for  k explicitly written. 
  ::解析度: 首先, 域名是除 x=0 外的所有真实数字, 所以 x=0 也是垂直的静态。 水平的静态是 y=0, 因为 k 没有明确写入没有值 。

  播放段落

  Let's make a table of values by choosing three values to each side of  $\begin{array}{r}x=0\end{array}$ . 
  ::让我们为 x=0 的每面选择三个值来绘制一个数值表。

  $$\begin{array}{r}x\end{array}$$	$$\begin{array}{r}y\end{array}$$
  $$\begin{array}{r}\text{-}4\end{array}$$	$$\begin{array}{r}\frac{1}{2}\end{array}$$
  $$\begin{array}{r}\text{-}2\end{array}$$	$$\begin{array}{r}1\end{array}$$
  $$\begin{array}{r}\text{-}1\end{array}$$	$$\begin{array}{r}1\end{array}$$
  	$$\begin{array}{r}\text{-}2\end{array}$$
  $$\begin{array}{r}2\end{array}$$	$$\begin{array}{r}\text{-}1\end{array}$$
  $$\begin{array}{r}4\end{array}$$	$$\begin{array}{r}\text{-}\frac{1}{2}\end{array}$$

  播放段落

  Plotting the points and using the asymptotes, we have the graph below. 
  ::绘制点图和使用小数图时,下图为图示。

  

  播放段落

  by Mathispower4u demonstrates how to determine the domain, complete a table of values, and graph a rational function. 
  ::通过 Mathispower4u 演示如何确定域, 完成一个数值表, 并绘制一个合理函数 。

   

  播放段落

  Example 4
  ::例4

  播放段落

  Graph $\begin{array}{r}y=\frac{1}{x-5}+2\end{array}$ . 
  ::图y=1x-5+2。

  播放段落

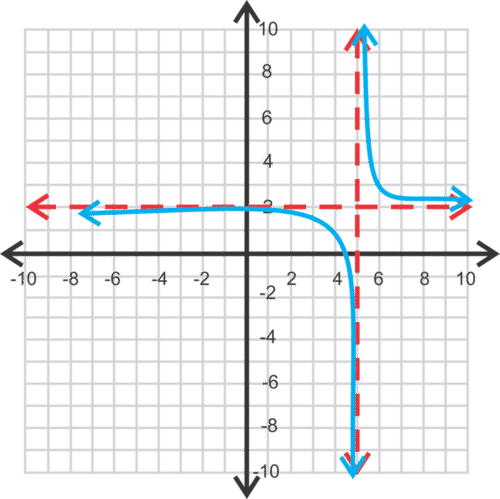
  Solution: For $\begin{array}{r}y=\frac{1}{x-5}+2\end{array}$ , the vertical asymptote is $\begin{array}{r}x=5\end{array}$ because that would make the denominator zero, and we cannot divide by zero. The horizontal asymptote is at  $\begin{array}{r}y=2\end{array}$ . Since these are asymptotes that are not also axes, we represent them with dashed lines to indicate that they are asymptotes, but not part of the graph.
  ::解析度 : 对于 y= 1x-5+2, 垂直静态为 x=5 , 因为这将使分母为零, 我们无法除以 0 。 水平静态为 y=2 。 由于这些是不同时是轴的静态, 我们用破折线来代表它们, 以表示它们为零, 但不在图形中 。

  播放段落

  Let's create a table of values. 
  ::让我们建立一个价值表。

  $\begin{array}{r}x\end{array}$	$\begin{array}{r}y\end{array}$
  0	$\begin{array}{r}1\frac{4}{5}\end{array}$
  2	$\begin{array}{r}1\frac{2}{3}\end{array}$
  3	$\begin{array}{r}1\frac{1}{2}\end{array}$
  6	3
  8	$\begin{array}{r}2\frac{1}{3}\end{array}$
  10	$\begin{array}{r}2\frac{1}{5}\end{array}$

  播放段落

  Drawing the asymptotes and plotting the points gives us the graph below. 
  ::绘制小点数和绘制点数时, 我们可以看到下面的图表 。

  

  播放段落

  Notice the shape and location of the branches are the same as the parent graph, just shifted to the right 5 units and up 2 units.
  ::注意树枝的形状和位置与母图相同, 刚刚移到右5个单元, 上两个单元 。

  播放段落

  Example 5
  ::例5

  播放段落

  The time to empty a tank by pumping out the contents varies inversely as the rate of pumping. Where g  is the number of gallons and  t  is the time in hours, how much is in a tank at 2 hours? At 5 hours? At 10 hours? 
  ::通过抽出罐装物来清空罐体的时间与抽水速度不同,反之亦然。加仑和吨位是几小时多少时间,2小时罐体内有多少时间?5小时,10小时?

  播放段落

  Solution:  We can describe this situation with the function  $\begin{array}{r}g=\frac{361.19}{t+3.2046}+\mathrm{186.29.}\end{array}$  The graph of this function is below.
  ::解答:我们可以用 g=361.19t+3.2046+186.29 函数来描述这种情况。此函数的图如下。

   

  播放段落

  By finding  $\begin{array}{r}t=2\end{array}$  on the t -axis, we can find the g -value, 255.688 gallons. Notice there are about 230 gallons after 5 hours, and 213 after 10 hours. 
  ::通过在t轴上发现 t=2,我们能找到255.688加仑的g值。 注意5小时后约有230加仑,10小时后有213加仑。

  播放段落

  by Mr. G demonstrates how to use transformations to graph rational functions. 
  ::由G先生介绍如何利用转换来绘制理性功能图。

   

  播放段落

  Example 6
  ::例6

  播放段落

  Find  a function that describes the graph below. 
  ::查找一个函数来描述下方的图形。

  

  播放段落

  Solution: We know that the numerator will be negative because the branches of this hyperbola are a reflection of the branches of the parent graph . The asymptotes are $\begin{array}{r}x=\text{-}3\end{array}$ and $\begin{array}{r}y=\text{-}4\end{array}$ . So far, we know $\begin{array}{r}y=\frac{a}{x+3}-4\end{array}$ . To determine $\begin{array}{r}a\end{array}$ , we can use the given $\begin{array}{r}x\end{array}$ - intercept .
  ::解答: 我们知道, 分子将会是负的, 因为此双曲线的分支是父形图的分支的反射。 微粒是 x= 3 和 y= 4 。 到目前为止, 我们了解 y= ax+ 3 - 4 。 要确定 a , 我们可以使用给定的 x 接口 。

   

  播放段落

  $$\begin{array}{rl}0& =\frac{a}{\text{-}3.75+3}\text{-}4\\ 4& =\frac{a}{\text{-}0.75}& & \text{The equation is}y=\frac{\text{-}3}{x+3}-4\\ \text{-}3& =a\end{array}$$

  
  ::0=-3.75+3-44=a-0.75 y=-3x+3-4-3=a

   

  播放段落

  How To Graph Rational Functions With a Graphing Utility
  ::如何用图形化工具图形化逻辑函数

  播放段落

  To graph a rational function with a graphing utility, enter the function into "y=" and press graph. To type the fraction , you may need to highlight the numerator and use the slash "/" key to get to the denominator. Also, remember to enclose the numerator and denominator in separate " data-term="Parentheses" role="term" tabindex="0"> parentheses . 
  ::要绘制带有图形工具的合理函数,请将函数输入“y=”和按键图形。要键入分数,您可能需要突出显示数字,并使用斜线“/”键才能到达分母。此外,请记住在单独的括号中附上数字和分母。

  播放段落

  WARNING
  ::警告

  播放段落

  Different graphing utilities represent asymptotes differently. For instance, in Desmos, there are no asymptotes shown at all. 
  ::不同的图形化功能代表的微粒不同。 例如, Desmos 完全没有显示微粒。

  

  播放段落

  On a TI-83, the graph has a solid vertical asymptote. 
  ::在TI -83上, 图表有一个坚固的垂直空位。

  

  播放段落

  When graphing, it is best to represent the asymptotes with dashed lines to indicate they have a role in the graph, but are not actually part of the graph (like a solid line). 
  ::当图形化时,最好用破折线代表小状线,以表明它们在图形中的角色,但实际上不是图形的一部分(如固线)。

  播放段落

  Summary
  ::摘要

  播放段落
  • To find the domain of a rational function, set the denominator equal to zero and solve the equation. The solutions should be eliminated from the real numbers to get the domain of the function. 
    ::要找到一个合理函数的域, 将分母设置为零, 并解析等式 。 解决方案应该从实际数字中删除, 才能获得函数的域 。
  播放段落
  • The vertical asymptote of a reciprocal function in standard form is  $\begin{array}{r}x=h,\end{array}$  and the horizontal asymptote is  $\begin{array}{r}y=k\end{array}$ . 
    ::标准格式对等函数的垂直时点为 x=h,水平时点为 y=k。
  播放段落
  • To graph a reciprocal function in standard form, determine the domain of the function (this will also be the location of the vertical asymptote), find the horizontal asymptote, and create a table of values with some values to the right of the vertical asymptote, and some to the left of the vertical asymptote.
    ::要用标准格式绘制一个对等函数,确定函数的域( 也将是垂直静态的位置) , 找到水平静态, 并创建一个含有垂直静态右侧某些值的数值表, 以及一些在垂直静态左侧的数值表 。

  播放段落

  Review
  ::回顾

  播放段落

  1. What are the asymptotes for $\begin{array}{r}y=\frac{2}{x+8}-3\end{array}$ ?
  ::1. y=2x+8-3的年数是多少?

  播放段落

  2. What are the asymptotes for $\begin{array}{r}y=6-\frac{1}{x-4}\end{array}$ ?
  ::2. y=6 - 1x - 4的微粒是什么?

  播放段落

  For problems 3-11, graph each rational function and state the equations of the asymptotes, the domain and range, and the intercepts.
  ::对于问题 3 -11, 请绘制每个合理函数的图表 并描述小行星的方程, 域和范围, 以及拦截的方程 。

  播放段落

  3. $\begin{array}{r}y=\frac{3}{x}\end{array}$
  ::3. y=3x

  播放段落

  4. $\begin{array}{r}y=\frac{1}{x}+6\end{array}$
  ::4. y=1x+6

  播放段落

  5. $\begin{array}{r}y=\text{-}\frac{1}{x}\end{array}$
  ::5.y=-1x

  播放段落

  6. $\begin{array}{r}y=\text{-}\frac{1}{x+3}\end{array}$
  ::6.y=-1x+3

  播放段落

  7. $\begin{array}{r}y=\frac{1}{x+5}\end{array}$
  ::7.y=1x+5

  播放段落

  8. $\begin{array}{r}y=\frac{1}{x-3}-4\end{array}$
  ::8.y=1x-3-4

  播放段落

  9. $\begin{array}{r}y=\frac{2}{x+4}-3\end{array}$
  ::9.y=2x+4-3

  播放段落

  10. $\begin{array}{r}y=\frac{5}{x}+2\end{array}$
  ::10. y=5x+2

  播放段落

  11. $\begin{array}{r}y=3-\frac{1}{x+2}\end{array}$
  ::11. y=3 - 1x+2

  播放段落

  Write functions that describe the graphs below. You may assume that a = 1.
  ::用于描述以下图表的写入函数。您可以假设a=1。

  12.

  

  13.

  

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. Write a function that satisfies the following: a vertical asymptote at  $\begin{array}{r}x=5\end{array}$  that goes through the point (6,4).
  ::1. 写出一个满足以下条件的函数:在 x=5 时直径点(6,4)的垂直衰减。

  播放段落

  2. Write a function that satisfies the following: a horizontal asymptote at  $\begin{array}{r}y=\text{-}2,\end{array}$  and a vertical asymptote at  $\begin{array}{r}x=\text{-}3\end{array}$ . 
  ::2. 写出满足以下条件的函数:y=2的横向同源物和x=3的垂直同源物。

  播放段落

  3.  Boyle's Law states that the pressure and volume of a gas are inversely proportional. 
  ::3. 《Boyle法》规定,气体的压力和体积是反比的。

  播放段落

  What does this mean? How does this represent an inversely proportional relationship?
  ::这是什么意思 这怎么代表反比例关系呢

  播放段落

  A bicycle pump is a great example that shows Boyle's Law. When you push down on the pump, the volume inside the bike pump decreases, and the pressure of the air increases so that it's pushed into the tire. If the volume inside of a bicycle pump is 8.2 cubic inches, and the pressure is 19.1 psi, we can find the equation that represents this situation. We know from Boyle's Law that the volume, "y", equals the constant divided by the pressure in psi. Our equation is $\begin{array}{r}y=\frac{156.62}{x}\end{array}$ . Graph this function. What is the relationship between the pressure and volume in this situation?
  ::自行车泵是Boyle法律的一个很好的例子。 当您推下泵时, 自行车泵的体积会下降, 气压会增加, 从而推入轮胎。 如果自行车泵的体积是8.2立方英寸, 压力是19.1 psi, 我们可以找到代表这种情况的方程式。 我们从 Boyle 法律中知道, 体积“ Y” 等于压力的常数除以 psi 。 我们的方程式是 y=156.62x. 图形这个函数。 在这种情况下, 压力和体积之间的关系是什么?

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see the Appendix. 
  ::请参看附录。

  播放段落

  PLIX
  ::PLIX

  播放段落

  Try these interactives that reinforce the concepts explored in this section:
  ::尝试这些强化本节所探讨概念的交互作用 :

  播放段落

  References
  ::参考参考资料

  播放段落

  1. "Boyle's Law," last edited May 15, 2017,
  ::1. 2017年5月15日 最后一次编辑的《鲍尔人法》