Course: 9.9 其他合理函数图示

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

绘制其他逻辑函数

A manufacturer wants to make cans that can hold 50 cubic inches of food—that is, the volume is 50 cubic inches. Which radius should be chosen to use the least material ?
::制造商想要制造罐头,罐头能容纳50立方英寸的食物,也就是说,容量是50立方英寸。应该选择哪个半径使用最少的材料?

We can consider different amounts of material by looking at a graph that compares the size of the radius to the amount of material used. This is a rational function that is not a reciprocal function in standard form . We discuss how to graph other rational functions in this section.
::我们可以通过查看一个将半径大小与所用材料数量作比较的图表来考虑不同数量的材料。这是一个理性函数,不是标准形式的对等函数。我们讨论如何在本节中绘制其他合理函数的图表。

lesson content

Vertical Asymptotes and Removable Discontinuities
::垂直单位和可移动断开

In this concept, we will extend to graphing rational functions—that is, rational functions of the form $\begin{aligned} f (x) = \frac{p (x)}{q (x)} \end{aligned}$ .
::在这个概念中,我们将扩展至绘制合理函数的图表——即表f(x)=p(x)q(x)的合理函数。

While vertical asymptotes can still occur when the denominator is equal to zero, there is another possibility that did not occur in standard form. The other possibility is that the domain problem can cause a hole or a removable discontinuity .
::虽然当分母等于零时仍可能发生垂直微粒,但另一种可能性不是以标准形式出现,另一种可能性是域问题可能造成孔或可移动的不连续性。

Vertical Asymptotes and Removable Discontinuities
::垂直单位和可移动断开

To find these, factor the numerator and the denominator.
::要找到这些,请乘以分子和分母。

There is a vertical asymptote when you CANNOT cancel the factor in the denominator with a factor in the numerator.
::当您无法取消分母中的分母因子与分子因子时,有一个垂直的零点。

There is a removable discontinuity when you CAN cancel the factor in the denominator with a factor in the numerator.
::当您可以取消分母中的分母因子与分子因子时,就会出现可移动的不连续性。

Example 1
::例1

Find any vertical asymptotes or removable discontinuities for the following functions:
::查找下列函数的任何垂直静态或可移动的不连续性:

a. $\begin{aligned} y = \frac{4 x - 5}{2 x + 7} \end{aligned}$
::a. y=4x-52x+7

b. $\begin{aligned} y = \frac{x^{2} - 4}{2 x^{2} - 5 x + 2} \end{aligned}$
::b. y=x2 - 42x2 - 5x+2

c. $\begin{aligned} y = \frac{3 x^{2} + 10}{x^{2} - 1} \end{aligned}$
::c. y=3x2+10x2-1

d. $\begin{aligned} y = \frac{x^{2} - 16}{x + 3} \end{aligned}$
::d. y=x2 - 16x+3

e. $\begin{aligned} y = \frac{2 x + 3}{6 x^{2} - x - 15} \end{aligned}$
::e. y=2x+36x2-x-15

Solution: For each of these functions, we need to factor the numerator and denominator to see whether or not we can cancel the factors in the denominator.
::解决办法:对于其中的每一项功能,我们需要将分子和分母考虑在内,以确定我们是否能够取消分母中的因素。

a. $\begin{aligned} y = \frac{4 x - 5}{2 x + 7} \end{aligned}$ : The numerator and denominator of this function are already prime factors. Since they are not the same, we cannot cancel them. Thus, there is a vertical asymptote where the denominator equals zero, $\begin{aligned} x = - \frac{7}{2} \end{aligned}$ .
::a. y=4x-52x+7:此函数的分子和分母已经是主要因素。由于它们不同,我们不能取消它们。因此,在分母等于0, x=-72的垂直静态中,分母等于零, x=-72。

b. $\begin{aligned} y = \frac{x^{2} - 4}{2 x^{2} - 5 x + 2} = \frac{(x + 2) (x - 2)}{(2 x - 1) (x - 2)} \end{aligned}$ : One of the factors in the denominator is the same as a factor in the numerator, so there is a removable discontinuity at $\begin{aligned} x = 2 \end{aligned}$ . Since the other factor cannot be canceled, there is a vertical asymptote at $\begin{aligned} x = \frac{1}{2} \end{aligned}$ .
::b. y=x2-42x2-5x+2=(x+2)(x-2)(x-2)(2x-1)(x-2)-2):分母的一个因素与分子中的系数相同,因此 x=2 存在可移动的不连续状态。由于其他系数不能取消,在 x=12 上有一个垂直的断裂状态。

c. $\begin{aligned} y = \frac{3 x^{2} + 10}{x^{2} - 1} = \frac{3 x^{2} + 10}{(x + 1) (x - 1)} \end{aligned}$ : Neither of the factors in the denominator can be canceled with the numerator, so there are two vertical asymptotes in the graph of this function at $\begin{aligned} x = - 1 \end{aligned}$ and $\begin{aligned} x = 1 \end{aligned}$ .
::c. y= 3x2+10x2- 1= 3x2+10(x+1)(x-1)-1:分子不能取消分母中的因数,因此在 x=-1 和 x=1 的函数图中,此函数的图中存在两个垂直的负位数。

d. $\begin{aligned} y = \frac{x^{2} - 16}{x + 3} = \frac{(x + 4) (x - 4)}{x + 3} \end{aligned}$ : The factor in the denominator does not cancel with the numerator. There is a vertical asymptote at $\begin{aligned} x = - 3 \end{aligned}$ .
::d. y=x2- 16x+3=(x+4)(x-4)x+3:分母中的系数不与分子取消。x= 3时有一个垂直的静态。

e. $\begin{aligned} y = \frac{2 x + 3}{6 x^{2} - x - 15} = \frac{2 x + 3}{(2 x + 3) (3 x - 5)} \end{aligned}$ : Like part b, this graph will have a vertical asymptote and a removable discontinuity. The vertical asymptote is at $\begin{aligned} x = \frac{5}{3}, \end{aligned}$ and the removable discontinuity is at $\begin{aligned} x = - \frac{3}{2} \end{aligned}$ .
::e. y= 2x+36x2-x-15=2x3x3(2x+3)(3x-5):与b部分一样,本图将有一个垂直的静态和可移动的不连续状态。垂直的静态在 x=53,可移动的不连续状态在x=32。

Horizontal and Oblique Asymptotes
::水平和尖尖缩缩数

Like the last concept, the still represent the end behavior of the function. However, in a more general setting, there are more possibilities. We introduce oblique or slanted asymptotes—for example, a line of the form $\begin{aligned} y = m x + b \end{aligned}$ . Three cases are outlined below.
::和上一个概念一样,它仍然代表着函数的最终行为。但是,在更一般的环境下,可能性更大。我们引入斜形或倾斜的微粒-例如,y=mx+b的直线。下面概述三个案例。

Horizontal and
::水平和水平

For a rational function of the form $\begin{aligned} f (x) = \frac{p (x)}{q (x)} = \frac{a_{m} x^{m} + \dots + a_{0}}{b_{n} x^{n} + \dots + b_{0}} \end{aligned}$ ,
::F(x)=p(x)q(x)=amxm+...+a0bnxn+...+b0,+b0,

If $\begin{aligned} m < n \end{aligned}$ , then there is a horizontal asymptote at $\begin{aligned} y = 0 \end{aligned}$ .
::如果 m < n, 那么y=0 就会有一个水平同位数。

If $\begin{aligned} m = n \end{aligned}$ , then there is a horizontal asymptote at $\begin{aligned} y = \frac{a_{m}}{b_{n}} \end{aligned}$ (ratio of the leading coefficients).
::如果 m=n, y= ambn (主要系数的比值) 就会有一个水平的同位数。

If $\begin{aligned} m = n + 1 \end{aligned}$ , then there is a oblique (slant) asymptote at $\begin{aligned} y = (a_{m} x^{m} + \dots + a_{0}) \div (b_{n} x^{n} + \dots + b_{0}) \end{aligned}$ without the remainder. A good estimate is $\begin{aligned} y = \frac{a_{m}}{b_{n}} x \end{aligned}$ .
::如果 m=n+1, 那么y= (amxm+...+a0)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Y=\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

If $\begin{aligned} m > n + 1 \end{aligned}$ , then there are no oblique asymptotes.
::如果 m>n+1, 那么就不会有斜面的单位数。

Example 2
::例2

Find any horizontal or oblique asymptotes for the following functions:
::为以下函数查找任何水平或倾斜的单弹道 :

a. $\begin{aligned} y = \frac{4 x - 5}{2 x + 7} \end{aligned}$
::a. y=4x-52x+7

b. $\begin{aligned} y = \frac{x^{2} - 4}{2 x^{2} - 5 x + 2} \end{aligned}$
::b. y=x2 - 42x2 - 5x+2

c. $\begin{aligned} y = \frac{3 x^{2} + 10}{x^{2} - 1} \end{aligned}$
::c. y=3x2+10x2-1

d. $\begin{aligned} y = \frac{x^{2} - 16}{x + 3} \end{aligned}$
::d. y=x2 - 16x+3

e. $\begin{aligned} y = \frac{2 x + 3}{6 x^{2} - x - 15} \end{aligned}$
::e. y=2x+36x2-x-15

Solution:
::解决方案 :

a. $\begin{aligned} y = \frac{4 x - 5}{2 x + 7} \end{aligned}$ : Since 1=1, this fits case 2, so there is a horizontal asymptote at $\begin{aligned} y = \frac{4}{2} = 2 \end{aligned}$ .
::a. y=4x-52x+7:自 1=1以来,此大小写为 2, 所以y=42=2时有一个水平同位数。

b. $\begin{aligned} y = \frac{x^{2} - 4}{2 x^{2} - 5 x + 2} \end{aligned}$ : This is also case 2. There is a horizontal asymptote at $\begin{aligned} y = \frac{1}{2} \end{aligned}$ .
::b. y=x2 - 42x2 - 5x+2: 也属于例2。y=12有一个水平同位数。

c. $\begin{aligned} y = \frac{3 x^{2} + 10}{x^{2} - 1} \end{aligned}$ : There is a horizontal asymptote at $\begin{aligned} y = \frac{3}{1} = 3 \end{aligned}$ .
::c. y= 3x2+10x2 - 1:y= 31= 3 上有一个水平同位数。

d. $\begin{aligned} y = \frac{x^{2} - 16}{x + 3} \end{aligned}$ : Since $\begin{aligned} 2 > 1 + 1 \end{aligned}$ , this falls into case 3. There is a slant asymptote at $\begin{aligned} y = \frac{1}{1} x = x \end{aligned}$ .
::d. y=x2 - 16x+3:自 2>1+1 起,这属于案件3 。y= 11x=x 上有一个倾斜微粒。

e. $\begin{aligned} y = \frac{2 x + 3}{6 x^{2} - x - 15} \end{aligned}$ : Here, $\begin{aligned} 1 < 2 \end{aligned}$ . This is case 1. There is a horizontal asymptote at $\begin{aligned} y = 0 \end{aligned}$ .
::e. y= 2x+36x2-x- 15: 这里, 1 < 2 。这是例1。 y= 0 是一个水平的单点。

by Mathispower4u demonstrates how to determine the vertical and horizontal asymptotes of rational functions.
::由 Mathispower4u 演示如何确定理性函数的垂直和水平空格。

Graphing Rational Functions
::图形推理函数

How To Graph Rational Functions
::如何图形逻辑函数

1. Find the domain of the function.
::1. 确定职能领域。

2. Find any vertical asymptotes or removable discontinuities.
::2. 找出任何垂直的微粒或可移动的不连续情况。

3. Find any horizontal asymptotes or oblique asymptotes.
::3. 找到任何水平的单单位或倾斜的单位。

4. Find any intercepts .
::4. 寻找任何拦截。

5. Create a table of values to fill out the graph.
::5. 创建用于填报图表的数值表。

Let's consider an example.
::让我们举个例子。

Example 3
::例3

Graph $\begin{aligned} y = \frac{1}{x^{2}} \end{aligned}$ .
::图y=1x2。

Solution: First, the domain of this function is all real numbers except 0, because $\begin{aligned} x = 0 \end{aligned}$ is a solution to $\begin{aligned} x^{2} = 0 \end{aligned}$ . This also helps us with the vertical asymptote, which is $\begin{aligned} x = 0 \end{aligned}$ .
::解析度: 首先, 此函数的域是除 0 外的所有真实数字, 因为 x= 0 是 x2= 0 的解析度。这也有助于我们使用 x= 0 的垂直静态, 也就是 x= 0 。

This function fits case 1, so there is a horizontal asymptote at $\begin{aligned} y = 0 \end{aligned}$ .
::此函数符合大小写 1, 所以在 y=0 时会有一个水平同位数。

Since the axes are the asymptotes, there are no intercepts. Let's fill out the graph with a table of values.
::由于轴是小数点, 因此没有拦截。让我们用一个数值表填入图表。

x	y
-2	$\begin{aligned} \frac{1}{4} \end{aligned}$
-1	1
$\begin{aligned} - \frac{1}{2} \end{aligned}$	4
$\begin{aligned} \frac{1}{2} \end{aligned}$	4
1	1
2	$\begin{aligned} \frac{1}{4} \end{aligned}$

The graph is below.
::图表如下。

Example 4
::例4

Graph $\begin{aligned} f (x) = \frac{2 x - 1}{x + 4} \end{aligned}$ .
::图f(x)=2x-1x+4。

Solution: T he domain is all real numbers; $\begin{aligned} x \neq - 4 \end{aligned}$ . We find the vertical asymptote, the value that makes the denominator zero. In this case, $\begin{aligned} x = - 4 \end{aligned}$ .
::解析度: 域名是所有真实数字; x 4。我们发现垂直无线值, 也就是分母为零的值。在此情况下, x= 4 。

The horizontal asymptote is $\begin{aligned} y = 2 \end{aligned}$ . Next, we find the x- and y- intercepts.
::水平空位为 Y=2 。下一步, 我们发现 X 和 y 界面。

$\begin{aligned} y \end{aligned}$ - intercept (when $\begin{aligned} x = 0 \end{aligned}$ ): $\begin{aligned} y = \frac{2 \cdot 0 - 1}{0 + 4} = - \frac{1}{4} \end{aligned}$
::y 拦截( 当 x=0 时 ) y= 2\0 - 10+4= 14

$\begin{aligned} x \end{aligned}$ -intercept (when $\begin{aligned} y = 0 \end{aligned}$ ):

\begin{aligned} 0 & = \frac{2 x - 1}{x + 4} \\ 0 & = 2 x - 1 \\ 1 & = 2 x \\ \frac{1}{2} & = x \end{aligned}

::x 拦截( 当y=0 时): 0= 2x- 1x+40= 2x- 11= 2x12=x

When solving for the $\begin{aligned} x \end{aligned}$ -intercept, to get the denominator out, we multiplied both sides by $\begin{aligned} x + 4 \end{aligned}$ . But when we multiply anything by 0, it remains 0. Therefore , to find the $\begin{aligned} x \end{aligned}$ -intercept, we need only set the numerator equal to zero and solve for $\begin{aligned} x \end{aligned}$ .
::当解析 X 接口时, 要将分母取出, 我们将两边乘以 x+4 。但是当我们乘以 0. 0 时, 它仍为 0 。因此, 要找到 x 接口, 我们只需要将数字设为 0 和 x 的解答。

Let's make a table.
::让我们做一张桌子。

$\begin{aligned} x \end{aligned}$	$\begin{aligned} y \end{aligned}$
$\begin{aligned} - 13 \end{aligned}$	$\begin{aligned} 3 \end{aligned}$
$\begin{aligned} - 7 \end{aligned}$	$\begin{aligned} 5 \end{aligned}$
$\begin{aligned} - 5 \end{aligned}$	$\begin{aligned} 11 \end{aligned}$
$\begin{aligned} - 3 \end{aligned}$	$\begin{aligned} - 7 \end{aligned}$
$\begin{aligned} - 1 \end{aligned}$	$\begin{aligned} - 1 \end{aligned}$
	$\begin{aligned} - 0.25 \end{aligned}$
$\begin{aligned} 2 \end{aligned}$	$\begin{aligned} 0.5 \end{aligned}$
$\begin{aligned} 5 \end{aligned}$	$\begin{aligned} 1 \end{aligned}$
$\begin{aligned} 14 \end{aligned}$	$\begin{aligned} 1.5 \end{aligned}$

lesson content

by Mathispower4u demonstrates how to graph rational functions.
::由 Mathispower4u 演示如何绘制理性函数。

Example 5
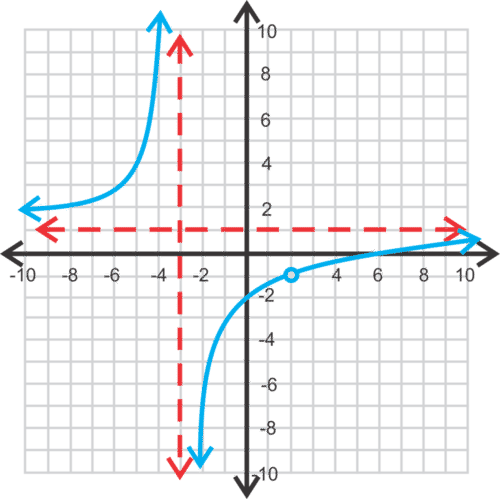
::例5

Graph $\begin{aligned} f (x) = \frac{x^{2} - 8 x + 12}{x^{2} - x - 6} \end{aligned}$ .
::图f(x)=x2-8x+12x2-x-6。

Solution: The domain is $\begin{aligned} {x \in R | x \neq 2, - 3} \end{aligned}$ . Let's factor the numerator and denominator to find the intercepts and vertical asymptotes.
::解析度 : 域是 {xRx2, 2, 3} 。让我们将分子和分母乘以找到拦截和垂直静态。

\begin{aligned} f (x) = \frac{x^{2} - 8 x + 12}{x^{2} + x - 6} = \frac{(x - 6) (x - 2)}{(x + 3) (x - 2)} \end{aligned}

x) =x2-8x+12x2+x-6=(x-6)(x-2)(x+3)(x-2)

Notice that the numerator and denominator both have a factor of $\begin{aligned} x - 2 \end{aligned}$ . Therefore, $\begin{aligned} x = 2 \end{aligned}$ is a hole. And, the output value that corresponds with the hole is not part of the range . In this example, $\begin{aligned} f (2) = \frac{2 - 6}{2 + 3} = \frac{- 4}{6} = - \frac{2}{3} \end{aligned}$ is not part of the range.
::注意分子和分母都有 x-2 的系数。因此, x= 2 是一个洞。而且, 与洞相对应的输出值不是范围的一部分。在此示例中, f(2)=2- 62+3=- 46=-23 不属于范围的一部分。

There is a vertical asymptote at $\begin{aligned} x = - 3 \end{aligned}$ and a zero at $\begin{aligned} x = 6 \end{aligned}$ . The horizontal asymptote is at $\begin{aligned} y = 1 \end{aligned}$ .
::在 x=3 和 x=6 上有一个垂直的静态,在 x=3 和 x=6 上有一个零。水平的静态在 y=1 上。

lesson content

Example 6
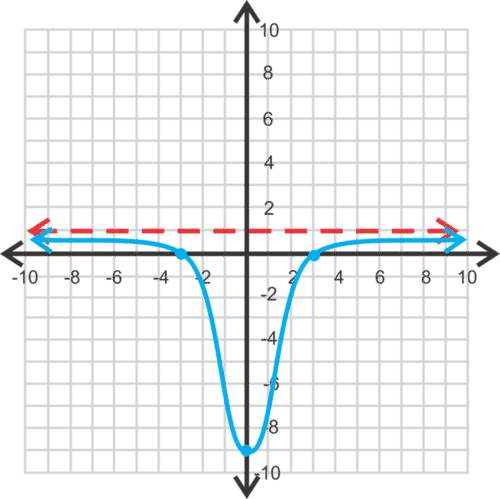
::例6

Graph $\begin{aligned} f (x) = \frac{x^{2} - 9}{x^{2} + 1} \end{aligned}$ .
::图f(x)=x2-9x2+1。

Solution: $\begin{aligned} y \end{aligned}$ -intercept: $\begin{aligned} y = \frac{- 9}{1} = - 9 \end{aligned}$ ; $\begin{aligned} x \end{aligned}$ -intercepts: $\begin{aligned} 0 = x^{2} - 9 \to x = \pm 3 \end{aligned}$ ; horizontal asymptote: $\begin{aligned} y = 1 \end{aligned}$ ; vertical asymptote: none; domain: $\begin{aligned} R \end{aligned}$ ; range: $\begin{aligned} R; y \neq 1 \end{aligned}$
::溶解度: Y- 截取值: y=- 91=- 9; x- 截取值: 0=x2- 9x% 3; 水平淡化值: y= 1; 垂直淡化值: 无; 域 : R; 范围: R; y 1

lesson content

by Mathispower4u demonstrates how to determine the domain, complete a table of values, and graph a rational function.
::通过 Mathispower4u 演示如何确定域, 完成一个数值表, 并绘制一个合理函数。

Example 7
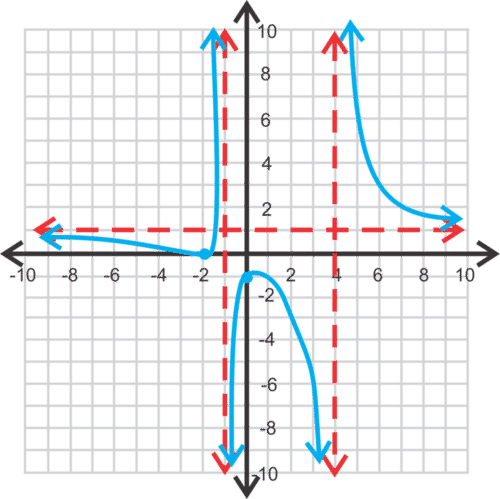
::例7

Graph $\begin{aligned} f (x) = \frac{x^{2} + 4 x + 4}{x^{2} - 3 x - 4} \end{aligned}$ .
::图f(x)=x2+4x+4x2-3x-4。

Solution: Let's factor the numerator and denominator to find the intercepts and vertical asymptotes.
::解答:让我们将分子和分母乘以寻找拦截和垂直静态。

\begin{aligned} f (x) = \frac{x^{2} + 4 x + 4}{x^{2} - 3 x - 4} = \frac{(x + 2) (x + 2)}{(x - 4) (x + 1)} \end{aligned}

\begin{aligned} x \end{aligned}

-intercept:

\begin{aligned} (- 2, 0) \end{aligned}

\begin{aligned} y \end{aligned}

-intercept:

\begin{aligned} (0, - 1) \end{aligned}

::f(x) =x2+4x+4x+4x2-3x-4=(x+2)(x+2)(x-4)(x+1)(x+1) x 拦截

2) -0, y 拦截

0,-1)

horizontal asymptote: $\begin{aligned} y = 1 \end{aligned}$
::水平时间: y=1

vertical asymptotes: $\begin{aligned} x = 4 \end{aligned}$ and $\begin{aligned} x = - 1 \end{aligned}$
::垂直空点数: x=4 和 x=-1

lesson content

Example 8
::例8

Graph $\begin{aligned} f (x) = \frac{x^{2} + 7 x - 30}{x + 5} \end{aligned}$ .
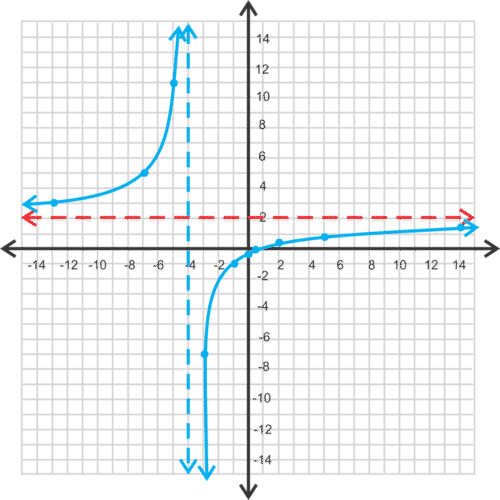
::图f(x)=x2+7x-30x+5。

Solution: The domain would be all real numbers; $\begin{aligned} x \neq - 5 \end{aligned}$ . In this example, the degree of the numerator is greater than the degree of the denominator. T here is a slant asymptote: $\begin{aligned} y = x + 2 - \frac{40}{x + 5} \end{aligned}$ or $\begin{aligned} y = x + 2 \end{aligned}$ . The $\begin{aligned} y \end{aligned}$ -intercept is $\begin{aligned} \frac{- 30}{5} \to (0, - 6), \end{aligned}$ and the $\begin{aligned} x \end{aligned}$ -intercepts are the solutions to the numerator, $\begin{aligned} x^{2} + 7 x - 30 = 0 \to (x + 10) (x - 3) \to x = - 10, 3. \end{aligned}$ There is a vertical asymptote at $\begin{aligned} x = - 5 \end{aligned}$ .
::解析度 : 域名将全部为真实数字 ; x -5 。在此示例中, 分子的度大于分母的度。有倾斜无序 : y= x +2 - 40x+5 或 y= +2 。 y 界面是 - 305}( 0 ) - 6 , x 界面是分子的解析度, x2+ 7x- 30= 0( x+10) (x-3)x=- 10, 3. 在 x= 5 有垂直无线。

lesson content

Example 9
::例9

Graph $\begin{aligned} y = \frac{3 x + 5}{2 x^{2} + 9 x + 20} \end{aligned}$ .
::图y=3x+52x2+9x+20。

Solution: $\begin{aligned} x \end{aligned}$ -intercept: $\begin{aligned} (- \frac{5}{3}, 0) \end{aligned}$ , $\begin{aligned} y \end{aligned}$ -intercept: $\begin{aligned} (0, \frac{1}{4}) \end{aligned}$
::解答: x 拦截-53,0) y 拦截: (0,14)

horizontal asymptote: $\begin{aligned} y = 0 \end{aligned}$
::水平时间: y=0

vertical asymptotes: none (Note: This is a possibility when the denominator is never equal to 0.)
::垂直等量数 : 无 (注: 当分母从不等于 0 时, 这是可能性。)

lesson content

Example 10
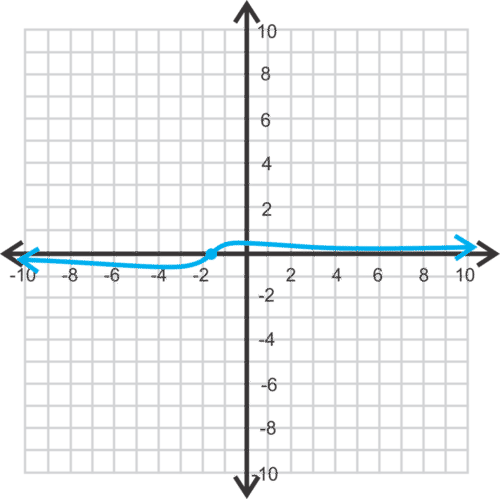
::例10

A manufacturer wants to make cans that can hold 50 cubic inches of food—that is, the volume is 50 cubic inches. Which radius should be chosen to use the least material?
::制造商想要制造罐头,罐头能容纳50立方英寸的食物,也就是说,容量是50立方英寸。应该选择哪个半径使用最少的材料?

Solution: The volume of a cylinder is $\begin{aligned} V = π r^{2} h, \end{aligned}$ and we want the volume to be 50 cubic inches. The surface area of the cylinder is $\begin{aligned} S = 2 π r h + 2 π r^{2} . \end{aligned}$ Solving for h in the volume equation , we have $\begin{aligned} h = \frac{50}{π r^{2}} \end{aligned}$ . Substituting this into the equation for the surface area, we have
::解析度: 气瓶的体积是 Vr2h, 我们希望气瓶的体积为 50 立方英寸。气瓶的表面面积是 S= 2rh+2r2. 溶解量方程式中的 h, 我们有 h= 50°r2 。将其转换为表面积的方程式, 我们发现

\begin{aligned} S & = 2 π r h + 2 π r^{2} \\ = 2 π r (\frac{50}{π r^{2}}) + 2 π r^{2} \\ = \frac{100}{r} + 2 π r^{2} \end{aligned}

The graph of this equation is below.
::S=2rh+2r2=2r(50r2)+2r2=100r+2r2 本方程图如下。

Notice the is not a line here. For positive values of r , it appears as though the minimum is at $\begin{aligned} r = 2 \end{aligned}$ . The radius of the can should be 2 inches to minimize the material used.
::通知不是一行。对于r的正值,似乎最低值为r=2,其半径应为2英寸,以尽量减少使用的材料。

Summary
::摘要

To find the vertical asymptote or removable discontinuity, factor the numerator and the denominator. There is a vertical asymptote when you CANNOT cancel the factor in the denominator with a factor of the numerator. There is a removable discontinuity when you CAN cancel the factor in the denominator with a factor of the numerator.
::要找到垂直的零时点或可移动的不连续性,请乘以分子和分母。当您无法使用分子系数来取消分母中的分母系数时,会有一个垂直的零时点和分母。如果您能够用分子系数来取消分母中的分母系数,则会有一个可移动的不连续性。

If $\begin{aligned} m < n \end{aligned}$ , then there is a horizontal asymptote at $\begin{aligned} y = 0 \end{aligned}$ .
::如果 m < n, 那么y=0 就会有一个水平同位数。

If $\begin{aligned} m = n \end{aligned}$ , then there is a horizontal asymptote at $\begin{aligned} y = \frac{a_{m}}{b_{n}} \end{aligned}$ (ratio of the leading coefficients).
::如果 m=n, y= ambn (主要系数的比值) 就会有一个水平的同位数。

If $\begin{aligned} m = n + 1 \end{aligned}$ , then there is a oblique (slant) asymptote at $\begin{aligned} y = (a_{m} x^{m} + \dots + a_{0}) \div (b_{n} x^{n} + \dots + b_{0}) \end{aligned}$ without the remainder. A good estimate is $\begin{aligned} y = \frac{a_{m}}{b_{n}} x \end{aligned}$ .
::如果 m=n+1, 那么y= (amxm+...+a0)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Y=\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

If $\begin{aligned} m > n + 1 \end{aligned}$ , then there are oblique asymptotes.
::如果 m>n+1, 则有倾斜的单位数。

To graph a rational function, find the domain of the function. Find any vertical asymptotes or removable discontinuities. Find any horizontal asymptotes or oblique asymptotes. Find any intercepts. Create a table of values to fill out the graph.
::要绘制一个合理函数,请找到函数的域。找到任何垂直的单位或可移动的不连续状态。找到任何水平的单位或倾斜的单位。查找任何拦截。创建一个数值表以填充图形。

Review
::回顾

Find the vertical and horizontal/slant asymptotes of the following functions:
::查找下列函数的垂直和水平/倾斜杂念:

1. $\begin{aligned} y = \frac{x - 2}{x + 7} \end{aligned}$
::1. y=x-2x+7

2. $\begin{aligned} y = \frac{x - 2}{x^{2} + 6 x + 8} \end{aligned}$
::2. y=x-2x2+6x+8

3. $\begin{aligned} y = \frac{x^{2} - 4}{x + 5} \end{aligned}$
::3. y=x2 - 4x+5

4. $\begin{aligned} y = \frac{x^{2}}{x - 3} \end{aligned}$
::4. y=x2x-3

Graph the rational functions below. Write down the equations of the asymptotes, the domain and range, and $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ intercepts. Identify any holes.
::绘制下面的理性函数。写下小数方程式、域和范围、 x 和 y 拦截的方程式。标明任何洞。

5. $\begin{aligned} y = \frac{x + 3}{x - 5} \end{aligned}$
::5. y=x+3x-5

6. $\begin{aligned} y = \frac{3 - x}{2 x + 10} \end{aligned}$
::6. y=3-x2x+10

7. $\begin{aligned} y = \frac{x + 1}{x^{2} - x - 12} \end{aligned}$
::7. y=x+1x2-x-12

8. $\begin{aligned} y = \frac{x - 7}{2 x^{2} - 11 x - 21} \end{aligned}$
::8.y=x-72x2-11x-21

9. $\begin{aligned} y = \frac{x^{2} + 5 x + 6}{x^{2} - 8 x + 12} \end{aligned}$
::9. y=x2+5x+6x2-8x+12

10. $\begin{aligned} y = \frac{x^{2} + 4}{2 x^{2} + x - 3} \end{aligned}$
::10. y=x2+42x2+x-3

11. $\begin{aligned} y = \frac{2 x^{2} - x - 10}{3 x^{2} + 10 x + 8} \end{aligned}$
::11. y=2x2-x-103x2+10x+8

12. $\begin{aligned} y = \frac{x^{2} - 4}{x^{2} + 3 x - 10} \end{aligned}$
::12. y=x2 - 4x2+3x- 10

13. $\begin{aligned} y = \frac{x^{2} + x - 30}{x + 6} \end{aligned}$
::13. y=x2+x-30x+6

14. $\begin{aligned} y = \frac{x^{3} - 2 x^{2} - 3 x}{x^{2} - 5 x + 6} \end{aligned}$
::14. y=x3-2x2-3x2-5x6

Explore More
::探索更多

1. True or False: If the numerator and denominator have the same degree and they are both linear polynomials, then the asymptote will be vertical.
::1. 真实或假的:如果分子和分母具有相同的程度,而且两者都是线性多元分子,则该分子和分母将是垂直的。

2. True or False: If the degree of the numerator is smaller than the degree of the denominator by 1, then the horizontal asymptote will be $\begin{aligned} y = 1 \end{aligned}$ .
::2. 真实或假:如果分子的度小于分母 1 的分母度,则水平的单点为y= 1 。

3. How many vertical asymptotes does $\begin{aligned} f (x) = \frac{1}{x^{2} + 2} \end{aligned}$ have?
::3. f( x) = 1x2+2 有多少垂直微粒?

4. Determine the slant asymptote of $\begin{aligned} y = \frac{3 x^{2} - x - 10}{3 x + 5} \end{aligned}$ . Now graph this function. Is there really a slant asymptote? Can you explain your results?
::4. 确定 y= 3x2- x- 103x+5 的倾斜无序点。现在绘制此函数的图。是否真的存在倾斜无序点? 您能否解释您的结果 ?

5. Darnell says that the function $\begin{aligned} y = \frac{2 x^{4} + 5}{x^{4} - 16} \end{aligned}$ has two vertical asymptotes, Barb says it has only one, and Aruna says it has four. Who is correct?
::5. Darnell说,y=2x4+5x4-16的函数有两个垂直微粒,Barbal说它只有一个,Aruna说它有四个。谁是正确的?

6. Xerxes says that the function $\begin{aligned} y = \frac{x - 2}{4 x^{2} + 7} \end{aligned}$ has a horizontal asymptote of $\begin{aligned} y = \frac{1}{4} \end{aligned}$ , Yolanda says the function has no horizontal asymptote, Zeb says it does have a horizontal asymptote, but it's at $\begin{aligned} y = 0 \end{aligned}$ . Who is correct?
::6. Xerxes 表示函数 y=x- 24x2+7 具有 Y=14 的水平同位数, Yolanda 表示函数没有水平同位数, Zeb 表示它确实有水平同位数, 但是它在y=0 。谁正确 ?

7. Farmer Joe raises rabbits. The population of Farmer Joe’s rabbits follow the formula $\begin{aligned} r (t) = \frac{200 t}{t + 1}, \end{aligned}$ where $\begin{aligned} t > 0 \end{aligned}$ represents the number of months since Farmer Joe began raising the rabbits. Graph $\begin{aligned} r (t) \end{aligned}$ for $\begin{aligned} t > 0 \end{aligned}$ . What trend do you notice in Farmer Joe's rabbit population over time?
::7. 农乔养兔:农乔的兔子数量遵循公式r(t)=200tt+1, 其中t>0代表农乔开始养兔子后的月数。图r(t)为t>0。你注意到农乔的兔子数量在一段时间内有什么趋势?

8. When a medicine is injected into a patient, the concentration (in mg/L) of the medicine in the patient's bloodstream can be modeled by the formula
::8. 当药物注入病人体内时,病人血液中药物的浓度(毫克/升)可以用公式模拟。

$\begin{aligned} m (t) = \frac{20 t}{t^{2} + 1} \end{aligned}$ . Graph $\begin{aligned} m (t) \end{aligned}$ for $\begin{aligned} t > 0 \end{aligned}$ . What trend do you notice in the concentration of the medicine in the patient’s blood over time?
::m(t) = 20t2+1. t>0的图m(t). 你注意到药物在病人血液中的浓度有何种趋势?

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try these interactives that reinforce the concepts explored in this section:
::尝试这些强化本节所探讨概念的交互作用 :

Section outline

General

绘制其他逻辑函数

Vertical Asymptotes and Removable Discontinuities ::垂直单位和可移动断开

Vertical Asymptotes and Removable Discontinuities ::垂直单位和可移动断开

Example 1 ::例1

Horizontal and Oblique Asymptotes ::水平和尖尖缩缩数

Horizontal and ::水平和水平

Example 2 ::例2

Graphing Rational Functions ::图形推理函数

How To Graph Rational Functions ::如何图形逻辑函数

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Example 9 ::例9

Example 10 ::例10

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

Vertical Asymptotes and Removable Discontinuities
::垂直单位和可移动断开

Vertical Asymptotes and Removable Discontinuities
::垂直单位和可移动断开

Example 1
::例1

Horizontal and Oblique Asymptotes
::水平和尖尖缩缩数

Horizontal and
::水平和水平

Example 2
::例2

Graphing Rational Functions
::图形推理函数

How To Graph Rational Functions
::如何图形逻辑函数

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Example 8
::例8

Example 9
::例9

Example 10
::例10

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX