课程： 12.4 抛物线 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节抛物体

折叠展开
抛物体
A radio telescope collects incoming radio waves from a broad area of sky via a large parabolic antenna (or dish), and then focuses those incoming radio waves onto a smaller antenna called the feed horn, which carries the waves to a radio receiver. The larger the dish, the greater the amount of data that can be collected, and the larger the surface area of the parabola , the fainter the electromagnetic radiation that can be detected. The dish needs to be parabolic in order to reflect the incoming waves to the feed horn so they can be collected, but also wide enough to collect as much data as possible ¹ .
::无线电望远镜通过大型抛物线天线(或天线)从宽广的天空区域收集无线电波,然后将射电波集中到一个较小的天线上,即把电波传送到无线电接收器上的小号天线上,将电波传送到无线电接收器上。天线越大,可以收集的数据就越多,抛物线的表面面积越大,可以检测到的电磁辐射就越微弱。天线需要是抛物线,才能将电波反映到电波传到电线角上,从而可以收集,但也足够广,可以收集尽可能多的数据。

If the cross section of a dish can be modeled by $\begin{aligned} x = 30 y^{2} - 10 y \end{aligned}$ , then how wide is the dish if the dish is half as deep as the focus? We cover parabolas like this in this section.
::如果盘子的横截面可以由 x=30y2 - 10y 模拟, 那么盘子的宽度是多少, 如果盘子的深度与焦点的深度是一半? 我们在本节中覆盖像这个的parolas 。

The Geometry of Parabolas
::Parabolas的几何测量

In the chapter on quadratic functions, we looked at parabolas as graphs of quadratic functions. In this section, we are focused on the equation for the shape of a parabola, and are not concerned about whether the parabola is oriented in such a way that it represents a function. We can define parabolas entirely by their geometric properties.
::在关于二次函数的一章中,我们把parbolas作为二次函数的图形来看待。在本节中,我们侧重于抛物线形状的方程,不关心抛物线的方向是否代表一种函数。我们可以完全用它们的几何特性来定义parbolas。

Geometry of Parabolas
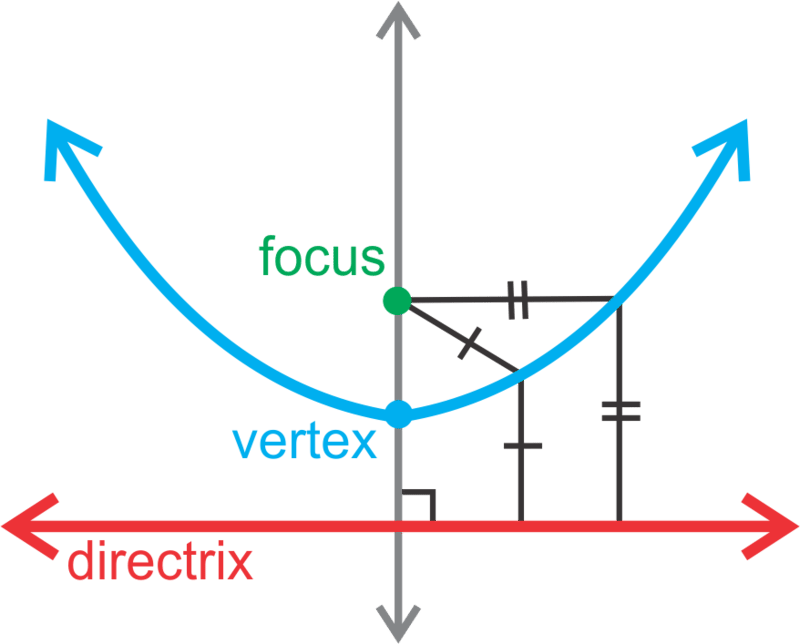
::Parabolas的几何测量

A parabola is a curve such that any point on the curve is equidistant from another point, called the focus , and a line called the directrix .
::抛物线是一个曲线,因此曲线上的任何点从另一个点(称为焦点)和直线(称为直线)的位置相等。

Equidistant means equally distant, so in this case, any point on the curve is the same distance from the focus and the directrix.
::等距意味着同样遥远所以在这种情况下曲线上的任何点都与焦点和准点的距离相同

The focus is a point on the axis of symmetry of the parabola. The directrix is perpendicular to the axis of symmetry. The points on the parabola—for example, t he vertex—are halfway between the focus and the directrix, as we can see in the image below.
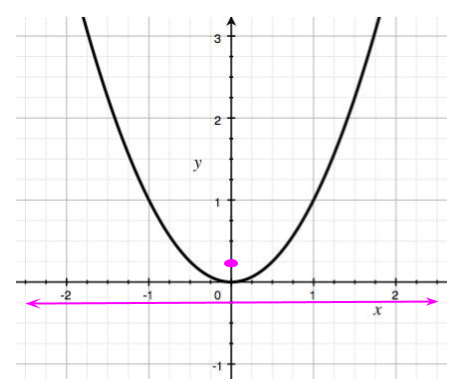
::焦点是抛物线对称轴上的点。直线与对称轴是垂直的。抛物线上的点( 例如, 脊椎) 在焦点和对称轴之间有一半, 我们从下面的图像中可以看到这一点。

Let's consider a familiar example. Below is a graph of $\begin{aligned} y = x^{2} . \end{aligned}$
::下面是y=x2的图表。

The points on this graph are equidistant from the line $\begin{aligned} y = - \frac{1}{4}, \end{aligned}$ which is the directrix, and the point $\begin{aligned} (0, \frac{1}{4}), \end{aligned}$ which is the focus.
::此图上的点与 y= 14 线( y= 14) 的 y= 14 线( irectrix) 和 ocus ( 0, 14) 点( occount) 相距相当。

Equations of Parabolas
::百万分数平方

We need to consider two standard forms of the equation for a parabola, depending on whether the axis of symmetry is horizontal or vertical.
::我们需要考虑抛物线方程的两种标准形式,取决于对称轴是横向还是纵向。

Standard Form of the Equation of a Parabola
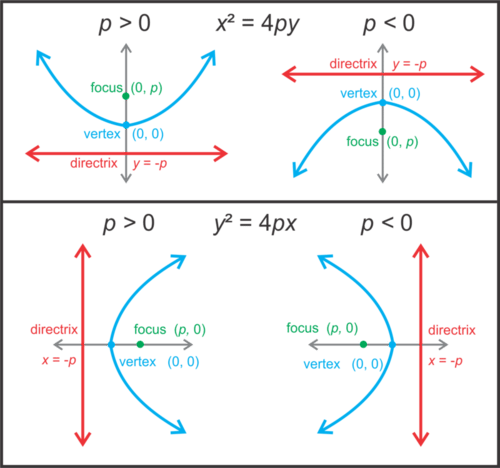
::帕拉波拉标准方程式标准方程式

Vertical Axis of Symmetry
::垂直对称轴轴

$\begin{aligned} (x - h)^{2} & = 4 p (y - k) \end{aligned}$

:x-h)2=4p(y-k)

The vertex is $\begin{aligned} (h, k) \end{aligned}$ and the focus is $\begin{aligned} (h, k + p) \end{aligned}$ . If the vertex is at the origin, the equation is $\begin{aligned} x^{2} = 4 p y \end{aligned}$ .
::顶点是 (h, k) , 焦点是 (h, k+p) 。如果顶点在源头, 则方程式为 x2=4py 。

Horizontal Axis of Symmetry
::水平对称轴

$\begin{aligned} (y - k)^{2} = 4 p (x - h) \end{aligned}$

:y-k)2=4p(x-h)

The vertex is $\begin{aligned} (h, k) \end{aligned}$ and the focus is $\begin{aligned} (h + p, k) \end{aligned}$ . If the vertex is at the origin, the equation is $\begin{aligned} y^{2} = 4 p x \end{aligned}$ .
::顶点是 (h, k) , 焦点是 (h+p, k) 。如果顶点在源头, 则公式为 y2= 4px 。

In both cases above, p is the distance from the vertex to the focus or from the vertex to the directrix.
::在以上两种情况中,p是从顶部到焦点的距离,或从顶部到直线的距离。

For parabolas with a vertex at the origin, the focus and the directrix are as below.
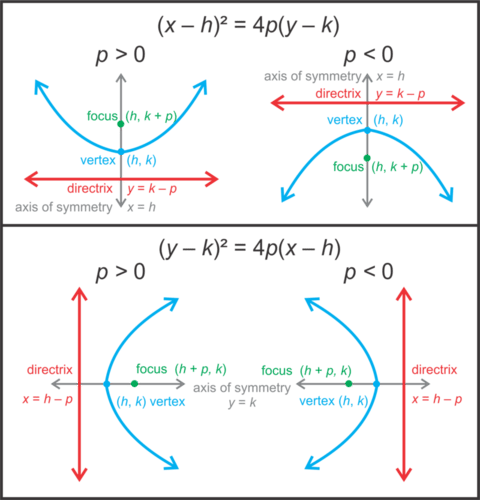
::对于原点有顶点的parabolas, 其焦点和准点如下。

If the vertex is not at the origin, finding the focus and directrix is a little more complicated. See the image below to help you find these values. Notice that the way we find the focus and directrix does not change whether $\begin{aligned} p \end{aligned}$ is positive or negative.
::如果顶点不是源头, 找到焦点和指向会比较复杂一些。请看下面的图像来帮助您找到这些值。注意我们找到焦点和指向的方式不会改变 p 是正的还是负的。

Example 1
::例1

Find the equation of the parabola below.
::找到下面的抛物线方程。

Solution: The vertex is at the origin and the parabola has a vertical axis of symmetry, so the equation will be $\begin{aligned} x^{2} = 4 p y \end{aligned}$ . The directrix is $\begin{aligned} y = 5 \end{aligned}$ , which means that $\begin{aligned} p = - 5 \end{aligned}$ . Substituting -5 for $\begin{aligned} p \end{aligned}$ , we have $\begin{aligned} x^{2} = - 20 y \end{aligned}$ .
::解析 : 顶点在源头, 抛物线具有对称的垂直轴, 所以方程将是 x2=4py。直线是 y= 5 , 这意味着 p= 5。 p 的替代 - 5, 我们有 x2= 20y 。

Example 2
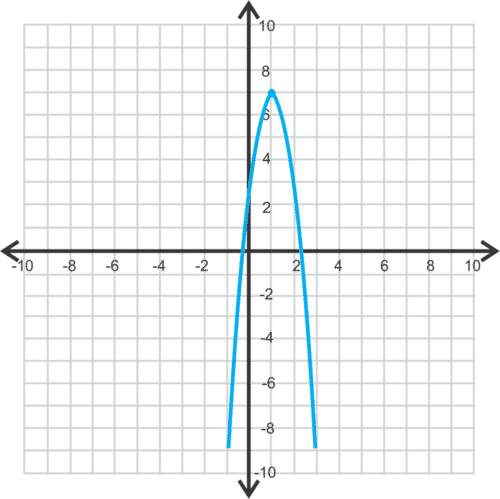
::例2

Analyze the equation $\begin{aligned} (y - 1)^{2} = 8 (x + 3) \end{aligned}$ . Find the vertex, axis of symmetry, focus, and directrix. Then determine if the function opens up, down, left, or right.
::分析方程 (y- 1) 2=8( x+ 3) , 找到对称、焦点和指向轴的顶部、轴。然后确定函数向上、下、左或右打开。

Solution: First, because $\begin{aligned} y \end{aligned}$ is squared, we know that the parabola will open to the left or right. We can conclude that the parabola will open to the right because 8 is positive, meaning that $\begin{aligned} p \end{aligned}$ is positive. Next, the vertex is $\begin{aligned} (- 3, 1) \end{aligned}$ and the axis of symmetry is $\begin{aligned} y = 1 \end{aligned}$ . Setting $\begin{aligned} 4 p = 8 \end{aligned}$ , we have that $\begin{aligned} p = 2 \end{aligned}$ . Adding $\begin{aligned} p \end{aligned}$ to the $\begin{aligned} x \end{aligned}$ -value of the vertex, we get the focus, $\begin{aligned} (- 1, 1) \end{aligned}$ . Subtracting $\begin{aligned} p \end{aligned}$ from the $\begin{aligned} x \end{aligned}$ -value of the vertex, we get the directrix, $\begin{aligned} x = - 5 \end{aligned}$ .
::解答 : 首先, 因为 y 是正方的, 我们知道抛物线会向左或右打开。我们可以得出结论, 抛物线会向右打开, 因为 8 是正的, 意味着 p 是正的。接下来, 顶点是 (3, 1) , 对称轴是 y= 1 。设置 4p= 8, 我们得到 p= 2 。将 p 添加到顶点的 x 值上, 我们得到焦点, (-1, 1) 从顶点的 x 值上扣减 p , 我们得到直线, x= 5 。

by mathlady40 shows how to find the equation of a parabola given the vertex and the focus.
::以 Mathlady40 显示如何根据顶点和焦点找到抛物线的方程。

Example 3
::例3

Find the vertex, focus, axis of symmetry, and directrix of $\begin{aligned} (x + 5)^{2} = 2 (y + 2) \end{aligned}$ .
::查找(x+5)2=2(y+2)的顶部、焦点、对称轴和直线。

Solution: The vertex is $\begin{aligned} (- 5, - 2) \end{aligned}$ and the parabola opens up, because $\begin{aligned} p \end{aligned}$ is positive and $\begin{aligned} x \end{aligned}$ is squared. $\begin{aligned} 4 p = 2 \end{aligned}$ , making $\begin{aligned} p = 2 \end{aligned}$ . The focus is $\begin{aligned} (- 5, - 2 + \frac{1}{2}) \end{aligned}$ or $\begin{aligned} (- 5, - \frac{3}{2}) \end{aligned}$ , the axis of symmetry is $\begin{aligned} x = - 5 \end{aligned}$ , and the directrix is $\begin{aligned} y = - 2 - \frac{1}{2} \end{aligned}$ or $\begin{aligned} y = - 4 \end{aligned}$ .
::解析度: 顶端为 (5, 2) , 抛物线打开, 因为 p是正数, x是正数。 4p=2, making p=2 。焦点是 (5, 2+12) 或 (5, 32) , 对称轴是 x= 5, 直线是 y=-2-12 或 y= 4 。

Example 4
::例4

The vertex of a parabola is $\begin{aligned} (- 2, 4) \end{aligned}$ and the directrix is $\begin{aligned} y = 7 \end{aligned}$ . Find the equation of the parabola.
::抛物线的顶部是 (-2,4) , 直线是 y= 7 。找到抛物线的方程。

Solution: First, let's determine the orientation of this parabola. Because the directrix is horizontal, we know the parabola will open up or down. We also know the directrix is above the vertex, so the parabola opens down. $\begin{aligned} p \end{aligned}$ will be negative.
::解答: 首先, 让我们来决定这个抛物线的方向。因为直线是水平的, 我们知道抛物线会向上或向下打开。我们还知道直线在顶部之上, 所以抛物线会向下打开。 p 将是负的。

To find $\begin{aligned} p \end{aligned}$ , we can use the vertex, $\begin{aligned} (h, k) \end{aligned}$ and the equation for a horizontal directrix, $\begin{aligned} y = k - p \end{aligned}$ .
::要找到p, 我们可以使用顶点, (h, k) 和横向直线的方程, y=k- p 。

$\begin{aligned} 7 & = 4 - p \\ 3 & = - p & p is negative due to downward orientation of the parabola \\ - 3 & = p \end{aligned}$

::7=4-p3=-pp 由于抛物线-3向下倾斜,负值为负值p

Now, using standard form, $\begin{aligned} (x - h)^{2} = 4 p (y - k) \end{aligned}$ , we can find the equation of this parabola.
::现在,使用标准格式 (x-h) 2=4p(y-k), 我们可以找到这个抛物线的方程式。

$\begin{aligned} (x - (- 2))^{2} & = 4 (- 3) (y - 4) \\ (x + 2)^{2} & = - 12 (y - 4) \end{aligned}$

:x-2)2=4(-3)(y-4)(x+2)2=-12(y-4)

Example 5
::例5

Find the equation of the parabola with vertex $\begin{aligned} (- 5, - 1) \end{aligned}$ and focus $\begin{aligned} (- 8, - 1) \end{aligned}$ .
::查找抛物线的方程式,其中加上顶部(5-1)和焦点(8,-1)。

Solution: The vertex is $\begin{aligned} (- 5, - 1) \end{aligned}$ , so $\begin{aligned} h = - 5 \end{aligned}$ and $\begin{aligned} k = - 1 \end{aligned}$ . The focus is $\begin{aligned} (- 8, - 1) \end{aligned}$ , meaning that the parabola will be horizontal. We know this because the $\begin{aligned} y \end{aligned}$ -values of the vertex and focus are both -1. Therefore, $\begin{aligned} p \end{aligned}$ is added or subtracted to $\begin{aligned} h \end{aligned}$ .
::解决方案 : 顶点是 (-5,-1), 所以 h=-5 和 k=-1。焦点是 (-8,-1) , 意思是 parbola 是水平的。我们知道这一点, 因为顶点和焦点的 Y 值是 - 1 。因此, p 被添加或减去到 h 。

$\begin{aligned} (h + p, k) ⟶ (- 8, - 1) \end{aligned}$ we can infer that $\begin{aligned} h + p = - 8 ⟶ - 5 + p = - 8 \end{aligned}$ and $\begin{aligned} p = - 3 \end{aligned}$ .
:h+p, k)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Therefore, the equation is $\begin{aligned} (y - (- 1))^{2} = 4 (- 3) (x - (- 5)) ⟶ (y + 1)^{2} = - 12 (x + 5) \end{aligned}$ .
::因此,等式是 (y- (-1) 2=4 (-3) (x- (5) ) (y+1) 2= 12 (x+5)。

Graphing Parabolas
::图示图

To graph a parabola, we can follow the steps below.
::以图示抛物线,我们可以遵循以下步骤。

How to Graph Parabolas
::如何绘制 Parabolas 图

1. Identify the vertex and $\begin{aligned} p \end{aligned}$ .
::1. 标明顶点和p。

2. Determine if the parabola opens up, down, right, or left. Find the focus.
::2. 确定抛物线是否向上、向下、向右或向左打开。

3. From the focus, count $\begin{aligned} 2 p \end{aligned}$ units perpendicular to the axis of symmetry in both directions. The length of the line segment that connects these two points and goes through the focus is $\begin{aligned} 4 p \end{aligned}$ . The line segment is called the latus rectum .
::3. 从焦点点向双向对称轴垂直计数 2p 单位,连接这两个点并贯穿焦点线段的长度为 4p。线段称为 latus 直肠。

4. Draw a parabola through the vertex and the two endpoints of the latus rectum.
::4. 通过拉图斯直肠的顶端和两端点绘制抛物线。

Example 6
::例6

Find the focus and directrix of $\begin{aligned} y^{2} = 6 x \end{aligned}$ . Then graph the parabola, the directrix, and the focus.
::查找 y2=6x 的焦点和直线。然后绘制抛物线、直线和焦点。

Solution: The vertex of this parabola is the origin. Solving for $\begin{aligned} p \end{aligned}$ , we have $\begin{aligned} 4 p = 6 ⟶ p = \frac{3}{2} \end{aligned}$ . Because $\begin{aligned} y \end{aligned}$ is squared and $\begin{aligned} p \end{aligned}$ is positive, the parabola will open to the right. The focus is $\begin{aligned} (\frac{3}{2}, 0) \end{aligned}$ and the directrix is $\begin{aligned} x = - \frac{3}{2} \end{aligned}$ . The two endpoints of the latus rectum are $\begin{aligned} (\frac{3}{2}, 3) \end{aligned}$ and $\begin{aligned} (\frac{3}{2}, - 3) \end{aligned}$ . With these two points and the vertex, we can draw the parabola below.
::解析 : 此抛物线的顶点是源。溶解 p, 我们有 4p=6p=32。由于 y 和 p 是正方和正方, 抛物线会向右打开。焦点是 (32, 0) , 直线是 x=-32. 。 latous 直肠的两个端点是 (32, 3) 和 (32, 3) 。有了这两个顶点和顶点, 我们可以在下面绘制 parbola 。

It is important to note that parabolas with a horizontal orientation are not functions because they do not pass the vertical line test.
::必须指出,横向方向的parabolas不是功能,因为它们没有通过垂直线测试。

Example 7
::例7

Analyze the equation $\begin{aligned} y^{2} = - 12 x \end{aligned}$ . Find the focus and directrix, and determine if the function opens up, down, left, or right. Then graph the parabola, the directrix, and the focus.
::分析 y2 = 12x 方程式。查找焦点和指向, 并确定函数向上、下、左或右打开。然后绘制抛物线、指向和焦点。

Solution: To find the focus and directrix, we need to find $\begin{aligned} p \end{aligned}$ . We can set $\begin{aligned} - 12 = 4 p \end{aligned}$ and solve for $\begin{aligned} p \end{aligned}$ .
::解决方案: 要找到焦点和主轴, 我们需要找到 p. 我们可以设置 - 12=4p 并解决 p.

$\begin{aligned} - 12 & = 4 p \\ - 3 & = p \end{aligned}$

::-12=4p-3=p 12=4p-3=p

Because $\begin{aligned} y \end{aligned}$ is squared, we know that the parabola opens to the left or right. Because $\begin{aligned} p \end{aligned}$ is negative, we know it is going to open to the left. Therefore, the focus is $\begin{aligned} (- 3, 0) \end{aligned}$ and the directrix is $\begin{aligned} x = 3 \end{aligned}$ .
::因为y是正方形, 我们知道抛物线向左或右打开。因为 p是负的, 我们知道它会向左打开。因此, 焦点是( 3, 0) , 直方向是 x=3 。

To graph the parabola, plot the vertex , which is the origin . Since $\begin{aligned} p = - 3 \end{aligned}$ , $\begin{aligned} 2 p = - 6 \end{aligned}$ , so from the focus we count up 6 units and down 6 units. That gives us the points $\begin{aligned} (- 3, 6) \end{aligned}$ and $\begin{aligned} (- 3, - 6) \end{aligned}$ , which are equidistant from the focus and directrix. They are both 6 units from each. The graph is below.
::要绘制抛物线图, 绘制顶点, 也就是源头。自 p= 3, 2p= 6, 所以从聚焦点开始, 我们数到6 个单位, 然后再数到6 个单位。这给我们提供了点数( 3, 6) 和 ( 3, 6) , 与焦点和直线相当。它们都是 6 个单位, 图表如下。

by Mathispower4u discusses the geometric definition of parabolas and how to graph a parabola.
::Mathispower4u讨论抛物线的几何定义以及如何绘制抛物线。

Example 8
::例8

Graph the parabola from Example 2. Plot the vertex, axis of symmetry, focus, and directrix.
::例 2. 绘制顶部、对称轴、焦点和直线。

Solution: First, plot all the values we found from Example 2. Then, from the focus at (-1,-1), we can count 4 units up and 4 units down to find the endpoints of the latus rectum. The graph is below.
::解决方案: 首先, 绘制我们从例2中发现的所有值, 然后, 从焦点点( 1, 1) , 我们可以向上数四个单位, 向下数四个单位, 以找到 latus 直肠的终点。图如下。

Example 9
::例9

Graph the parabola from Example 4.
::从例4中绘制抛物线图。

Solution:
::解决方案 :

Example 10
::例10

If the cross section of a satellite TV dish can be modeled by $\begin{aligned} x = 30 y^{2} - 10 y \end{aligned}$ , then how wide is the dish in feet if the dish is half as deep as the focus?
::如果卫星电视天线的横截面可以用 x=30y2 - 10y 做模型,那么如果天线的深度与焦点的一半一样深,天线的足部宽度是多少?

Solution: First we need to determine what the vertex and the focus are. We complete the square.
::解决方案:首先我们需要确定什么是顶端和焦点。我们完成广场。

$\begin{aligned} x & = 30 (y^{2} - \frac{1}{3} y) \\ x + 30 \cdot \frac{1}{36} & = 30 (y^{2} - \frac{1}{3} y + \frac{1}{36}) \\ x + \frac{5}{6} & = 30 (y - \frac{1}{6})^{2} \\ \frac{1}{30} (x + \frac{5}{6}) & = (y - \frac{1}{6})^{2} \end{aligned}$

::x=30(y2-13y)x+30-136=30(y2-13y+136)x+56=30(y-16)2130(x+56)=(y-16)2

The vertex is $\begin{aligned} (- \frac{5}{6}, \frac{1}{6}) . \end{aligned}$    $\begin{aligned} p \end{aligned}$ is $\begin{aligned} 4 p = \frac{1}{30} ⟶ p = \frac{1}{120} . \end{aligned}$ Since it is positive, the parabola opens to the right and the focus is $\begin{aligned} (\frac{5}{6} + \frac{1}{120}, \frac{1}{6}) ⟶ (\frac{101}{120}, \frac{1}{6}) . \end{aligned}$
::顶点是 (-56,16). p p 4p=130p=1120。由于它是正数, 抛物线向右打开, 焦点是 (56+1120, 16)\\( 101120, 16) 。

The $\begin{aligned} x \end{aligned}$ -coordinates for the opening of the dish are half the distance between the vertex and the focus: $\begin{aligned} \frac{5}{6} + \frac{1}{2} \cdot \frac{1}{120} = \frac{5}{6} + \frac{1}{240} = \frac{201}{240} = \frac{67}{80} . \end{aligned}$ If we find the $\begin{aligned} y \end{aligned}$ -coordinates, we can find the distance between them.
::打开盘子的x坐标是顶端和焦点之间的距离的一半:56+121120=56+1240=201240=6780。如果我们找到Y坐标,我们可以找到它们之间的距离。

$\begin{aligned} \frac{1}{30} (x + \frac{5}{6}) & = (y - \frac{1}{6})^{2} \\ \frac{1}{30} (\frac{67}{80} + \frac{5}{6}) & = (y - \frac{1}{6})^{2} \\ \frac{1}{30} (\frac{401}{240}) & = (y - \frac{1}{6})^{2} \\ \frac{401}{7, 200} & = (y - \frac{1}{6})^{2} \\ \pm \sqrt{\frac{401}{7, 200}} & = y - \frac{1}{6} \\ \pm \frac{\sqrt{401}}{60 \sqrt{2}} + \frac{1}{6} & = y \\ y & = \frac{\sqrt{401}}{60 \sqrt{2}} + \frac{1}{6} = 0.403 \\ y & = \frac{\sqrt{401}}{60 \sqrt{2}} - \frac{1}{6} = 0.069 \\ 0.403 - 0.069 = 0.334 \end{aligned}$

::130(x+56)=(y-16)2130(6780+56)=(y-16)2130(401240)=(y-16)24017 200=(y-16)2_4017 200=(y-16)2_4017 200=(y-16)16_401602+16=yy=401602+16=0.4003y=401602-16=0.0690.403-0.069=0.334

How to Graph Parabolas Using Desmos
::如何使用脱模图示 Parabolas

Enter the equations as is into Desmos. Remember to use the caret key ^ (Shift 6) for the exponents.
::输入 Desmos 中的方程式。记住要使用 {( Shift 6)\\\\\\\\\\\\\\\\\\\\\\\\\ x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ </span> </p> <p id="x-ck12-91x"> <span class="x-ck12-img-inline"> <img alt="" data-flx-url="/flx/show/THUMB_POSTCARD/image/user%3Acollegealgebra/1252383-1493399379-59-84-Screenshot-2017-04-28-13.05.20.png" data-imageresourceid="11047030" data-onerror="null" loading="lazy" onerror="null" src="https://dr282zn36sxxg.cloudfront.net/datastreams/f-d%3A62459258f38fa84dd2cdbcbb19d123617203bf74d3d70a16b91cf7a8%2BIMAGE_THUMB_POSTCARD_TINY%2BIMAGE_THUMB_POSTCARD_TINY.1" style="" width="300"/> </span> </p> </div> </div> <p id="x-ck12-MmIyZDljNjI4YmRlZWQwYTZhZjc1YTMzYjBlZmQ4YzA.-r3h"> </p> <div class="x-ck12-element-box" id="x-ck12-Yzk3ZjAyMjY4MGU0YWJiNGFmMGQ0YTQzODk0ODFiY2Q.-job"> <div class="x-ck12-element-box-header" id="x-ck12-MWQyMDM5NTcwNjYxNmU1YmQxZTdlNTI0ZTAyYzc3ZDE.-cjh"> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h3> <span> How to Graph Parabolas Using a TI-83/84 </span> <br/> <span style="color: green; "> ::如何使用TI-83/84来图示Parabolas </span> </h3> </div> <div class="x-ck12-element-box-body" id="x-ck12-ZWFkMTQ2MjVmYmQ1MTRiNmNhMmNhYzFmZGJjMjU1ZWE.-8t9"> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-Y2ZjNzAzNTNhZmQyNWY5YmZlYjcyZGJhODgwZTgxZjE.-8ws"> 1. Solve for <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="y"> <span class="MathJax_Preview" style="color: inherit; display: none;"> </span> <span class="MathJax_SVG" data-mathml='<math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" rowspacing="3pt" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" displaystyle="true"><mtr><mtd><mi>y</mi></mtd></mtr></mtable></math>' id="MathJax-Element-100-Frame" role="presentation" style="font-size: 100%; display: inline-block; position: relative;" tabindex="-1"> <svg aria-hidden="true" focusable="false" height="2.768ex" role="img" style="vertical-align: -0.809ex;" viewbox="0 -843.3 816.3 1191.7" width="1.896ex" xmlns:xlink="http://www.w3.org/1999/xlink"> <g fill="currentColor" role="group" stroke="currentColor" stroke-width="0" transform="matrix(1 0 0 -1 0 0)"> <use x="151" xlink:href="#MJMATHI-79" y="-47"> </use> </g> </svg> <span class="MJX_Assistive_MathML" role="presentation"> <math xmlns="http://www.w3.org/1998/Math/MathML"> <mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" displaystyle="true" rowspacing="3pt"> <mtr> <mtd> <mi> y </mi> </mtd> </mtr> </mtable> </math> </span> </span> </span> in the equation. <br/> <span style="color: green; "> ::1. 在等式中解决y。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-YzY3ZmFhN2Q1ZDYxYmIzMjcxMzA2MTkyN2RiNDc0MTQ.-vr5"> 2. Enter the equation under <strong> Y= </strong> . You can type in {-1,1} to indicate plus or minus.
::2. 在 Y= 下输入方程式。您可以输入 {-1,1} 以表示正负。

3. Press GRAPH . You will see both halves of the parabola.
::3. 按GRAPH。你会看到抛物线的两半。



Feature: I Can See Clearly
::特写:我能看得很清楚

by Deirdre Mundy
::由Deirdre Mundy 编辑

Look at your classmates. How many of them wear glasses? How many wear contacts? Many people depend on corrective lenses to help them see. How do the lenses work? By harnessing the power of parabolas.
::看看同学们,他们中有多少人戴眼镜?有多少人戴眼镜?有多少人戴眼镜?许多人依靠矫正镜来帮助他们看。眼镜如何工作?利用parapolas的力量。

Staying Focused
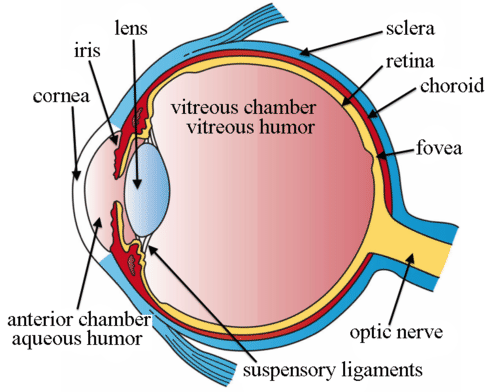
::保持焦点集中

Lenses are parabolic surfaces that collect light and focus it. The lens in your eye is a parabola. When it is formed correctly, it focuses images on your retina, the area at the back of your eye. If your lens is misshapen, it won't focus images on your retina. Its focal point will either be in front of or behind your retina, and the image on your retina will be blurry.
::视窗表面是抛光镜, 收集光并聚焦它。你眼中的镜头是一个抛光镜。当它被正确形成时, 它会将图像聚焦在视网膜上, 也就是你眼睛后面的视网膜上。如果您的视网膜上没有透镜, 它不会将图像聚焦在视网膜上。它的焦点要么在视网膜前面, 要么在视网膜后面, 视网膜上的图像将模糊不清。

Eye doctors create corrective lenses like eyeglasses and contacts to change the focal point of your eye's lens. By measuring the distortion in your vision, they can calculate how far to move your eye's focal point, and in what direction. Your corrective lenses are made specifically for your eyes, which is why they won't work for other people. Sometimes a person opts to undergo laser surgery. In this case, the eye doctor uses a laser to change the shape of the eye's lens. Since the shape of the parabola has changed, the focal point has also changed. Images focus on the retina, and the patient can live without eyeglasses.
::眼科医生创造矫正镜像眼镜和接触器, 以改变眼镜的焦点。通过测量视力的扭曲, 他们可以计算出你眼睛的焦点移动的距离, 以及方向。您的矫正镜是专门为你的眼睛制作的, 这就是为什么他们不会为其他人工作。有时一个人选择接受激光手术。在这种情况下, 眼科医生使用激光来改变眼镜的形状。由于抛光镜的形状已经改变, 焦点也已经改变。图像集中在视网膜上, 病人可以没有眼镜生活。

As people age, the proteins in their eyes begin to break down. Their lenses become cloudy, and they can't see as well because light cannot make it through the lens. These cloudy lenses are called cataracts. Today, doctors can remove the old lenses and replace them with new synthetic lenses. The new lenses often correct other vision problems as well, such as astigmatism, nearsightedness, and farsightedness, because they are constructed to focus light on the retina.
::随着人们的老化,他们眼中的蛋白质开始分崩离析。他们的镜片变得阴暗,他们看不到,因为光线无法通过镜片。这些云色的镜片被称为白内障。如今,医生可以移除旧的镜片,用新的合成镜片取而代之。新的镜片也常常纠正其他的视觉问题,如恶名主义、近视和远视,因为新造这些镜片是为了聚焦视网膜的光线。

by yahyarawat describes the different types of corrective lenses that are used to correct nearsightedness and farsightedness.
::yyyarawat描述了用来纠正近视和远视的不同类型的矫正透镜。



Summary
::摘要

A parabola is a curve such that any point on the curve is equidistant from another point, called the focus, and a line called the directrix.
::抛物线是一个曲线,因此曲线上的任何点从另一个点(称为焦点)和直线(称为直线)的位置相等。

The standard forms of the equation of a parabola are $\begin{aligned} (x - h)^{2} = 4 p (y - k) \end{aligned}$ for a vertical axis of symmetry and $\begin{aligned} (y - k)^{2} = 4 p (x - h) \end{aligned}$ for a horizontal axis of symmetry.
::抛物线方程的标准形式是(x-h)2=4p(y-k),对称垂直轴为(y-k)2=4p(x-h),对称横向轴为(y-k)=4p(x-h)。

To graph a parabola, find the vertex and $\begin{aligned} p \end{aligned}$ . Identify the focus and then count $\begin{aligned} 2 p \end{aligned}$ units away from the focus perpendicular to the axis of symmetry. Draw a parabola through the vertex and these two points.
::要绘制抛物线图,请找到顶点和 p. 标明焦点,然后从焦点垂直到对称轴的 2p 单位数。通过顶点和这两个点绘制一个抛物线。

Review
::回顾

Determine if the parabola opens to the left, right, up or down.
::确定抛物线是否向左、右、上或下打开。

1. $\begin{aligned} x^{2} = 4 y \end{aligned}$
::1. x2=4y

2. $\begin{aligned} y^{2} = - \frac{1}{2} x \end{aligned}$
::2. y2=12x

3. $\begin{aligned} x^{2} = - y \end{aligned}$
::3. x2=-y

Find the vertex, focus, axis of symmetry, and directrix of the parabolas below. Graph the result.
::查找以下参数的顶部、焦点、对称轴和直线。绘制结果。

4. $\begin{aligned} x^{2} = - 2 y \end{aligned}$
::4. x2=-2y

5. $\begin{aligned} y^{2} = \frac{1}{4} x \end{aligned}$
::5. y2=14x

6. $\begin{aligned} y^{2} = - 5 x \end{aligned}$
::6. y2=-5x

7. $\begin{aligned} x^{2} = 8 y \end{aligned}$
::7. x2=8y

8. $\begin{aligned} (x + 1)^{2} = - 3 (y - 6) \end{aligned}$
::8. (x+1)2=-3(y-6)

9. $\begin{aligned} (x - 3)^{2} = y - 7 \end{aligned}$
::9. (x-3-3)2=y-7

10. $\begin{aligned} (y + 2)^{2} = 8 (x + 1) \end{aligned}$
::10. (y+2)2=8(x+1)

11. $\begin{aligned} y^{2} = - 10 (x - 3) \end{aligned}$
::11. y2=-10(x-3)

12. $\begin{aligned} (x + 6)^{2} = 4 (y + 8) \end{aligned}$
::12.(x+6)2=4(y+8)

13. $\begin{aligned} (y - 5)^{2} = - \frac{1}{2} x \end{aligned}$
::13. (y-5)2=-12x

Find the equation of the parabola.
::找到抛物线的方程。

14. vertex: $\begin{aligned} (0, 0) \end{aligned}$ , focus: $\begin{aligned} (4, 0) \end{aligned}$
::14. 顶点0,0),重点4,0)

15. vertex: $\begin{aligned} (0, 0) \end{aligned}$ , directrix: $\begin{aligned} x = 10 \end{aligned}$
::15. 顶点: (0,0), 指向: x=10

16. vertex: $\begin{aligned} (0, 0) \end{aligned}$ , focus: $\begin{aligned} (0, \frac{7}{2}) \end{aligned}$
::16. 顶点0,0),重点0,72)

17. vertex: $\begin{aligned} (2, - 1) \end{aligned}$ , focus: $\begin{aligned} (2, - 4) \end{aligned}$
::17. 顶点2,-1),重点2,4)

18. vertex: $\begin{aligned} (- 3, 6) \end{aligned}$ , directrix: $\begin{aligned} x = 2 \end{aligned}$
::18. 顶点3,6),指向:x=2

19. vertex: $\begin{aligned} (6, 10) \end{aligned}$ , directrix: $\begin{aligned} y = 9.5 \end{aligned}$
::19. 顶点: (6,10),指向:y=9.5

20.

21.

Explore More
::探索更多

1. In the chapter on quadratic functions, the basic parabolic equation was $\begin{aligned} y = a x^{2} . \end{aligned}$ Now, we write $\begin{aligned} x^{2} = 4 p y \end{aligned}$ . Rewrite $\begin{aligned} p \end{aligned}$ in terms of $\begin{aligned} a \end{aligned}$ and determine how they affect each other.
::1. 在关于二次函数的一章中,基本抛物线方程为y=ax2.,现在,我们用一个字母写x2=4py,重写p,确定它们相互的影响。

2. a. Find the equation of the parabola with focus $\begin{aligned} (- 1, - 2) \end{aligned}$ and directrix $\begin{aligned} x = 3. \end{aligned}$
::2.a. 找出抛物线的方程式,重点(-1-2)和指向x=3。

b. Rewrite the equation of the parabola, $\begin{aligned} x^{2} - 8 x + 2 y + 22 = 0 \end{aligned}$ , in standard form by completing the square. Then find the vertex.
::b. 完成方形,以标准格式重写参数2-8x+2y+22=0的方程。然后找到顶点。

3. Use the distance formula, $\begin{aligned} d = \sqrt{{(x_{2} - x_{1})}^{2} - {(y_{2} - y_{1})}^{2}} \end{aligned}$ , to prove that the point $\begin{aligned} (4, 2) \end{aligned}$ is on the parabola $\begin{aligned} x^{2} = 8 y \end{aligned}$ .
::3. 使用距离公式d=(x2-x1)2-(y2-y1)2,以证明点(4,2)在抛物线x2=8y上。

4. A satellite dish is a three-dimensional parabola used to retrieve sound, TV, or other waves. Assuming the vertex is $\begin{aligned} (0, 0) \end{aligned}$ , where would the focus have to be on a satellite dish that is 4 feet wide and 9 inches deep? You may assume the parabola has a vertical orientation (opens up).
::4. 卫星天线是用于检索声音、电视或其他波浪的三维抛物线,假设顶端是0,0,那么重点必须放在宽4英尺、深9英寸的卫星天线上?你可以假定抛物线有垂直方向(打开)。

5. Your homework assignment is to find the focus of the parabola $\begin{aligned} (x + 4)^{2} = - 12 (y - 5) \end{aligned}$ . You say the focus is $\begin{aligned} (- 4, 5) \end{aligned}$ . Banu says the focus is $\begin{aligned} (0, - 3) \end{aligned}$ . Carlos says the focus is $\begin{aligned} (- 4, 2) \end{aligned}$ . Which one of you is correct?
::5. 你的家庭作业任务是找到抛物线(x+4)2=12(y-5)的焦点,你说焦点是(4),5),Banu说焦点是(0),3。Carlos说重点是(4),2你们中的哪一个是正确的?

6. Conic sections that share a focus are called confocal . Write equations for two distinct parabolas that are confocal.
::6. 共有焦点的二次曲线区段称为组合体,为组合体的两个不同的parapolas编写方程式。

7. A flashlight has a parabolic reflector whose cross section can be modeled by $\begin{aligned} y = \frac{1}{2} x^{2} . \end{aligned}$ Find the width of the flashlight in centimeters if the opening is 5 centimeters above the focus.
::7. 手电筒有一个抛物面反射器,其截面可由y=12x2模拟。如果开口在焦距上方5厘米,则用厘米来查找手电灯的宽度。

8. Water flows out of a spout in the middle of a fountain in a parabolic arc, according to the model $\begin{aligned} h = - \frac{1}{3} (x - 3)^{2} + 7 \end{aligned}$ . How wide does the circular pool around the fountain need to be to contain the water?
::8. 根据模型H=-13(x-3-3)2+7.,喷泉中央喷口中的喷口以抛光弧中流出的水流按照H=-13(x-3-3)2+7. 喷泉周围圆环池需要多少宽才能控制水?

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

References
::参考参考资料

"Radio Telescope | Astronomical Instrument | Britannica.com," by Kenneth I. Kellermann,
::由Kenneth I. Kellermann主演,

章节大纲

常规

抛物体

The Geometry of Parabolas ::Parabolas的几何测量

Geometry of Parabolas ::Parabolas的几何测量

Equations of Parabolas ::百万分数平方

Standard Form of the Equation of a Parabola ::帕拉波拉标准方程式标准方程式

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Graphing Parabolas ::图示图

How to Graph Parabolas ::如何绘制 Parabolas 图

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Example 9 ::例9

Solution: ::解决方案 :

Example 10 ::例10

How to Graph Parabolas Using Desmos ::如何使用脱模图示 Parabolas

Feature: I Can See Clearly ::特写:我能看得很清楚

Staying Focused ::保持焦点集中

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

References ::参考参考资料

The Geometry of Parabolas
::Parabolas的几何测量

Geometry of Parabolas
::Parabolas的几何测量

Equations of Parabolas
::百万分数平方

Standard Form of the Equation of a Parabola
::帕拉波拉标准方程式标准方程式

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Graphing Parabolas
::图示图

How to Graph Parabolas
::如何绘制 Parabolas 图

Example 6
::例6

Example 7
::例7

Example 8
::例8

Example 9
::例9

Solution:
::解决方案 :

Example 10
::例10

How to Graph Parabolas Using Desmos
::如何使用脱模图示 Parabolas

Feature: I Can See Clearly
::特写:我能看得很清楚

Staying Focused
::保持焦点集中

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

References
::参考参考资料