12.5圆
章节大纲
-
Without obstacles like mountains, the range of a radio signal is often circular. Like many New York radio (and television) stations, WHTZ, one of the most popular top 40 stations in the country, sends its signal from the top of the Empire State Building 1 . The signal travels a distance of approximately 75 miles. Trenton, New Jersey, is 34 miles west of New York City and 38 miles south. Philadelphia is 53 miles west and 60 miles south of New York City 2 . Does the radio signal from WHTZ reach either Trenton or Philadelphia?
::与许多纽约电台(和电视台)一样,WHTZ是该国最受欢迎的40个台站之一。 WHTZ从帝国大厦顶端发出信号,1 其距离大约75英里。新泽西特伦顿位于纽约市以西34英里处,南38英里处。费城位于纽约市以西53英里处,南60英里处。2 WHTZ的无线电信号是到达特伦顿还是费城吗?In this section, we discuss how to work with circles like the signal in this example.
::在本节中,我们讨论如何与象本例子中的信号那样的圈子合作。Geometry of Circles
::圆形的几何Until now, your only reference to circles was from geometry. In the coordinate plane, the definitions and terminology still apply.
::直到现在,你对圆圈的唯一引用来自几何。在坐标平面上,定义和术语仍然适用。Geometry of a Circle
::圆形的几何A circle is the set of points that are equidistant (the radius ) from a given point (the center ).
::a 圆是指从给定点(中心)到相等点(半径)的一组点。-
A line segment that has endpoints on the circle is called a
chord
.
::带有圆端点的线条段称为和弦。 -
A line segment that passes through the center and has endpoints on the circle is a
diameter
.
::直径是一个线段,它穿过中心,在圆上有端点。 -
A section of the circle is called an
arc
.
::圆的A部分称为弧。
by Sunshine22854 shows how to draw a circle using a compass.
::以“阳光22854”显示如何使用罗盘绘制圆形。Equations of Circles
::圆圆平To determine the equation of a circle, let's see how we can find one using an investigation.
::为了确定圆的方程,让我们看看如何通过调查找到一个。Investigation: Finding the Equation of a Circle
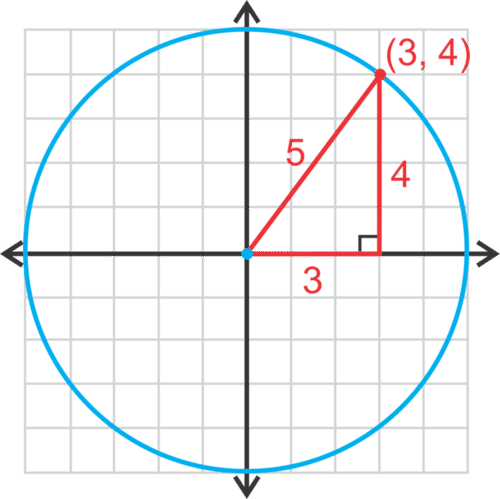
::调查:寻找圆圈的等同1. On a piece of graph paper, draw an plane. Using a compass, draw a circle, centered at the origin that has a radius of 5. Find the point on the circle and draw a right triangle with the radius as the hypotenuse.
::1. 在一张图纸上,绘制 x - y 平面。使用罗盘,绘制圆形,以半径为5的原点为中心,在圆上找到点(3, 4),并绘制以半径为下限的右三角形。2. Using the length of each side of the right triangle, show that the Pythagorean Theorem is true.
::2. 使用右三角形每一侧的长度,表明毕达哥里安理论是真实的。3. Now, instead of using , change the point to so that it represents any point on the circle. Using to represent the radius, rewrite the Pythagorean Theorem.
::3. 现在,与其使用( 3, 4) , 不如将点改为 ( x, y ) , 以便代表圆上的任何点。 使用 r 代表半径, 重写 Pythagorean 理论 。The equation of a circle , centered at the origin, is where is the radius and is any point on the circle. If we use transformations to move the center of our circle to , the equation will be the standard form of the equation of a circle .
::圆的方程式, 以原点为中心, 是 x 2 + y 2 = r 2, 其中 r 是圆半径, ( x , y) 是圆上的任何点。 如果我们使用变换将圆的中心移动到 (h, k) , 该方程式将是圆方程式的标准形式 。Standard Form of the Equation of a Circle
::圆形等量的标准格式where and are real numbers and is a non-negative number.If the center is the origin, then the standard form becomes
::如果中心是源头,那么标准形式就变成Example 1
::例1Find the equation of a circle with a center at the origin and a radius of .
::查找圆的方程式,在圆的起点和半径为 6 5 。Solution: Substitute for in .
::溶液: 以 r x 2 + y 2 = r 2 代替 6 5 r。Example 2
::例2Find the equation of the circle with center and radius 5.
::查找圆的方程式,以中间( 2, 4) 和半径 5 为中心。Solution: Substitute the center and radius values into the equation and simplify.
::溶液:将中间值和半径值替换为方程并简化。Example 3
::例3You draw a circle that is centered at . You measure the diameter of the circle to be 18 units. Does the point lie on the circle?
::您绘制了一个以 ( - 2, - 2) 为中心的圆形。 您测量圆形直径为 18 个单位。 点( 4, 5) 是否在圆形上?Solution: We are given that the center is , so and . We are also given the diameter of the circle, but we need the radius. Recall that the radius is half the diameter, so
::解答: 我们被告知中心是 ( - 2, - 2 ), 所以 h = - 2 和 k = - 2 。 我们也被给出圆的直径, 但我们需要半径 。 回顾半径是直径的一半, 所以 r = 18 2 = 9 。If we substitute these values into the equation for the circle, we get:
::如果我们将这些值替换为圆形方程,我们就会得到:Now, to find if the point lies on the circle, we substitute 4 for x and 5 for y, and see if the equation holds true.
::现在,要找到点( 4, 5) 是否在圆上, 我们用 4 代替 x, 5 取代 y, 看看方程是否正确 。Therefore, the point does not lie on the circle.
::因此,问题不在于圆圈上。by CK-12 shows how to find the equation of a circle when given a center and a radius.
::的 CK-12 显示当给定一个中点和半径时如何找到圆的方程式 。Example 4
::例4Find the equation of the circle with its center at the origin and that passes through .
::查找圆的方程式, 以圆的起点为中心, 穿过( - 7, - 7) 。Solution: Using the equation of the circle, we have: . Solve for .
::解决办法:使用圆的方程式,我们有-7) 2 + (-7) 2 = r 2 。
So, the equation is . The radius of the circle is .
::方程式是 x 2 + y 2 = 98。圆的半径是 r = 98 = 7 2 。Example 5
::例5Find the equation of the circle with center and on the circle.
::查找圆的方程式,在圆上以中间( 6, - 1) 和中间( 5, 2) 为中心。Solution: In this example, we are not given the radius. To find the radius, we can graph the points and use the Pythagorean Theorem or use the distance formula, .
::解答 : 在此示例中, 我们没有得到半径 。 要找到半径, 我们可以绘制点图, 使用 Pytagoren 理论, 或者使用距离公式, d = ( x 2 - x 1) 2 + ( y 2 - y 1) 2 。Therefore, the equation of this circle is or .
::因此,这个圆的方程式是 (x - 6) 2 + (y - (-1)) 2 = (10) 2 或 (x - 6) 2 + (y + 1) 2 = 10。by CK-12 shows how to find the equation of a circle when the radius is not known.
::的 CK-12 显示当半径未知时如何查找圆的方程式 。Example 6
::例6WHTZ sends its signal from the top of the Empire State Building 1 . The signal travels a distance of approximately 75 miles. Trenton, New Jersey, is 34 miles west of New York City and 38 miles south. Philadelphia is 53 miles west and 60 miles south of New York City 2 . Does the radio signal from WHTZ reach either Trenton or Philadelphia?
::WHTZ从帝国大厦顶端发送信号1。信号在大约75英里的距离内传送。新泽西州特伦顿位于纽约市以西34英里、南38英里处。费城位于纽约市以西53英里、南60英里处。2 WHTZ的无线电信号是到达特伦顿还是费城?Solution: If we say the Empire State Building is the origin, then the equation for the signal is since the radius is 75. Using the distance formula, we can determine if the points represented by Trenton (-34, -38) and Philadelphia (-53, -60) fit inside the circle or not.
::解答:如果我们说帝国大厦是源头, 那么信号的方程式是 x 2 + y 2 = 5, 625, 因为半径是 75, 使用距离公式, 我们可以确定 Trenton (-34, - 38) 和 Fixton (-53, - 60) 所代表的点是否在圆圈内。The signal reaches Trenton, but it does not reach Philadelphia.
::信号到达特伦顿, 但它没有到达费城。Example 7
::例7The endpoints of a diameter of a circle are and . Find the equation.
::圆形直径的终点是 ( - 3, 1) 和 ( 9, 6) 。 查找方程 。Solution: In this problem, we are not given the center or radius. We can find the length of the diameter using the distance formula, and then divide it by 2.
::解决方案 : 在此问题上, 我们没有得到中心或半径 。 我们可以使用距离公式找到直径的长度, 然后将其除以 2 。Now we need to find the center. Use the midpoint formula with the endpoints.
::现在我们需要找到中间点。使用中点公式与端点。Therefore, the equation is .
::因此,等式是(x - 3) 2 + (y - 7 2) 2 = 169 4。by Mathispower4u shows how to find the equation of a circle when given the endpoints of the diameter of the circle.
::在 Mathispower4u 中, 当给定圆直径的终点时, 显示如何找到圆的方程 。Graphing Circles
::图表圆To graph a circle, we need to identify points that we can find on the circle. Then we can connect them as a circle.
::要绘制圆形图,我们需要确定在圆形上可以找到的点。然后我们可以将它们连接成圆形。How to Graph a Circle
::如何绘制圆形1. Identify the center of the circle and the radius.
::1. 标明圆的中心和圆半径。2. Count the radius number of units away from the center to the right and to the left, up and down. That will give you four points.
::2. 将单位半径数从中间向右和向左、向上和向下计算,给予四点。3. Draw a circle through these four points.
::3. 通过这四个点绘制一个圆形。Let's see how this works with some examples.
::让我们用一些例子来研究一下这是怎么回事。Example 8
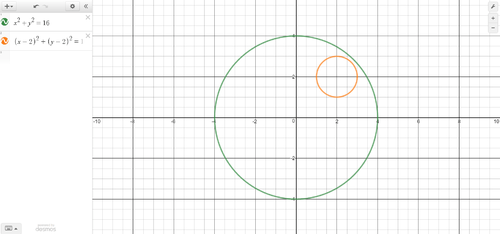
::例8Graph .
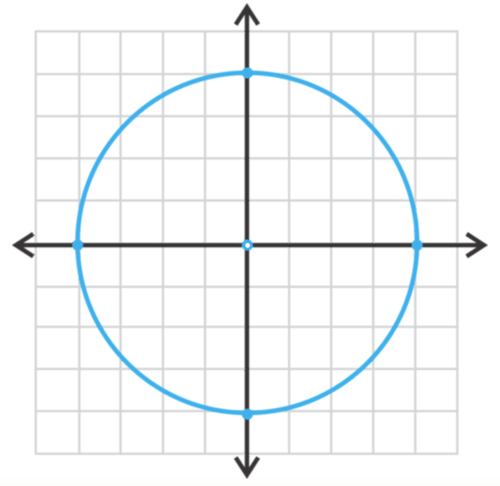
::图 x 2 + y 2 = 16 。Solution: This circle is centered at the origin. To find the radius, we can set , making . is not -4 because it is a distance and distances are always positive.
::解析度 : 此圆以原点为中心。 要找到半径, 我们可以设置 16 = r 2, 使 r = 4 . r = - 4 。 r 不是 - 4, 因为它是一个距离, 距离总是正数 。To graph the circle, start at the origin and go out 4 units in each direction: (4,0), (0,4), (-4,0), and (0,-4). Connect these points with a circle.
::绘制圆形图时,从原点开始,向每个方向取出4个单位4,0,0,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4。将这些点与圆形连接。
Example 9
::例9Find the center and radius of and graph.
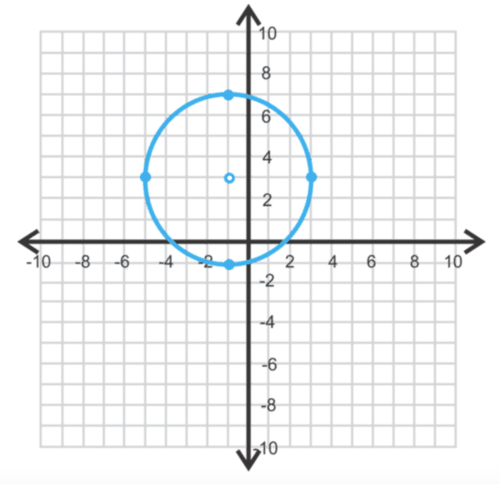
::查找( x + 1) 2 + ( y - 3) 2 = 16 和 图中的中心和半径。Solution: The center is and the radius is or 4. To graph, plot the center and then go out 4 units up, down, to the left, and to the right.
::解答:中心是 ( - 1, 3) , 半径是 16 或 4 。 要绘制图, 绘制中心, 然后向上、 向下、 向左、 向右走 4 个单元 。Example 10
::例10Graph and find the center and radius.
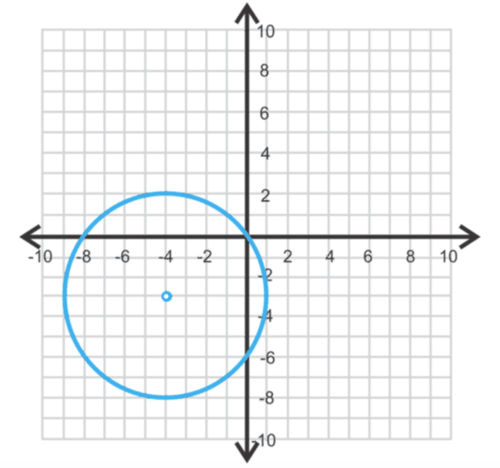
::图( x + 4) 2 + ( y + 3) 2 = 25 并找到中间和半径 。Solution: The center is and the radius is 5.
::解答:中心是 ( - 4, - 3) 半径是 5 。by M-Squared Tutorials demonstrates several examples of graphing a circle when given the equation.
::以 M-Squared Tuartictors 表示在给定方程式时绘制圆形图的几个例子。How to Graph Circles Using Desmos
::如何使用 Desmos 绘制圆形To graph a circle in Desmos, enter the equation as it is. Use parentheses if the center is not at the origin, and use the caret key (Shift 6) to type the exponent.
::要在 Desmos 中绘制圆形图,请按原样输入方程。如果中心不在源头,请使用括号括号,并使用注意键( Shift 6)键入引号。How to Graph Circles Using a TI-83/84
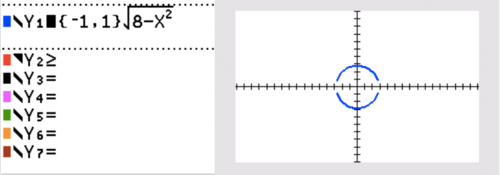
::如何使用 TI-83/84 来图形圆形To graph a circle with a TI-83/84, if the circle is centered at the origin, you can solve for and enter that result in Y=, using {-1,1} in front to get both halves of the circle.
::要用 TI-83/84 绘制圆形图,如果圆以原圆为中心,您可以用 {-1,1} 在前面使用 {-1,1} 来获取圆形的两半。Notice that the two halves of the circle are not connected around the -axis. This is common with graphing calculators. Also, notice that the image may not appear as a circle based on the window size. Choose to ZOOM: ZSquare or WINDOW, and choose the same width on the axes.
::请注意圆的两半角没有连接到 x - 轴周围。 这在图形计算器中很常见 。 另外, 注意图像不能以窗口大小为基础显示为圆形 。 选择 ZOOM: ZSquare 或 WINDOW, 并在轴上选择相同的宽度 。For any circle, you can select 2nd PRGM and then under the DRAW menu choose Circle. The format of the Circle command is Circle(h, k, r). Then press ENTER .
::对于任何圆,您可以选择 2 PRGM, 然后在 DRAW 菜单下选择圆。 圆形命令的格式是圆形( h、 k、 r) 。 然后按 ENTER 键 。Summary
::摘要-
A circle is a set of points that are equidistant from a center point.
::a 圆是一组从中点开始等距的点。 -
The standard form of an equation of a circle is
where
are the coordinates of the center and
is the radius.
::圆形方程式的标准形式是 (x- h) 2 + (y- k) 2 = r 2, 其中 (h, k) 是中心坐标, r 是半径。 -
To graph a circle, find the center and then count the radius number of units to the right, left, up, and down to get four points on the graph of the circle. Draw a circle to connect them.
::要绘制圆形图,请在圆形图上绘制圆形图,找到圆形中心,然后向右、向左、向上和向下计算单位的半径数,以获得圆形图上的四个点。绘制一个圆形以连接它们。
Review
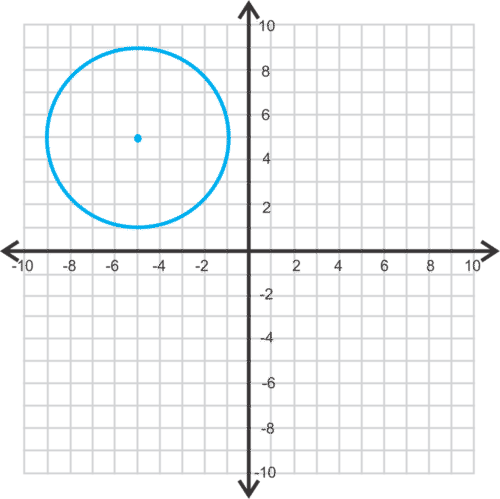
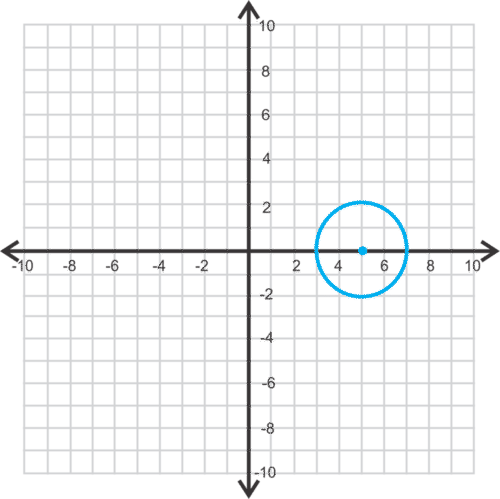
::回顾For questions 1-4, match the equation with the graph.
::对于问题14, 将方程式与图表匹配 。1.
::1. (x-8) 2 + (y + 2) 2 = 42.
::2. x 2+2+(y-6) 2=93.
::3. (x+2) 2 + (y-3) 2 = 364.
::4. (x - 4) 2 + (y + 4) 2 = 25Find the equation of the circle, given the information below.
::查找圆形的方程,并给出以下信息。5. center: origin; radius: 14
::5.中点:来源;半径:146. center: origin; radius:
::6.中中点:来源地;半径:9 27. center: ; radius: 7
::7 中 : ( - 3, - 3 ) ; 半径: 78. center: ; radius:
::8.中 8.中-7, 6 ) ; 半径: 15
9. center: origin; point on circle:
::9. 中点: 原点; 圆点7, - 24 )
10. center: origin; point on circle:
::10. 中枢: 来源; 圆上的点2 , 2 )
11. center: ; point on circle:
::11 中 : (8, - 1 ) ; 圆上的点 : (0, 14 )12. center: ; point on circle:
::12 中 : ( - 2, - 5 ) ; 圆上的点 : (3, 2 )13. diameter endpoints: and
::13. 直径端点-4,1)和(-6,3)
14. diameter endpoints: and
::14.直径端点5,-8)和(11,2)
15.
16.
17.
Graph the circles below. Find the center and radius.
::绘制下面的圆形图 找到中间和半径18.
::18. x 2 + y 2 = 6419.
::19. x 2 + y 2 = 5020.
::20. 2 x 2 + 2 y 2 = 16221.
::21. (x - 2) 2 + (y - 5) 2 = 1622.
::22. (x+4) 2 + (y+3) 2 = 1823.
::23. (x+7+7) 2+(y-1) 2=8Explore More
::探索更多1. In geometry, you learned about tangent lines to a circle. Recall that the tangent line touches a circle at one point, and is perpendicular to the radius at that point, called the point of tangency.
::1. 在几何学学到圆形的正切线。提醒注意,正切线在某一点触及圆形,与圆形的半径垂直,称为正切点。a. The equation of a circle is with point of tangency .
::a. 圆的方程式为x 2+y 2 = 10,有切点(- 3, 1) 。b. Find the slope of the radius from the center to .
::b. 查找半径的斜坡,从中间到(-3,1)c. Find the perpendicular slope to (a). This is the slope of the tangent line.
::c. 找到(a)的垂直斜坡,这是正切线的斜坡。d. Use the slope from (b) and the given point to find the equation of the tangent line.
::d. 使用(b)和给定点的斜坡查找正切线的方程。e. Repeat the steps to find the equation of the tangent line to with a point of tangency of .
::e. 重复查找正切线的方程式到 x 2 + y 2 = 34 的步骤,其相切点为 (3, 5 ) 。f. Find the equation of the tangent line to the circle with center and the point of tangency is .
::f. 将正切线的方程式与圆形的中间线(3, - 4)和正切点( - 1, 8)等同起来。2. One radio station is 30 miles east and 40 miles north of another radio station that broadcasts at the same frequency (or channel). If the range of the 1st radio station is 30 miles, and the range of the 2nd radio station is 25 miles, do the two signals overlap? (Hint: Graph the circles.)
::2. 一个无线电台在以同一频率(或频道)广播的另一个无线电台以东30英里和以北40英里处,如果第一无线电台的射程为30英里,而第二无线电台的射程为25英里,这两个信号是否重叠? (提示:绘制圆圈。 )3. Some submarines use SONAR to detect objects in the ocean. SONAR sends out a circular signal, or an arc of a circular signal, until one of the circles hits an object and bounces back 3 . If a submarine 5 miles south and 3 miles west detects an object 1 mile south and 1 mile east of its position, find an equation for the circular signal that intersected the object.
::3. 有些潜艇利用SONAR探测海洋中的物体,SONAR发出圆形信号或圆形信号弧,直到一个圆圈击中一个物体并反弹。如果一艘潜艇在南面5英里和西面3英里处探测到一个物体,在物体位置以南1英里和东面1英里处发现一个物体,则为该物体交叉的圆形信号找到一个方程式。4. The tallest Ferris wheel in the world is the High Roller in Las Vegas. If the Ferris wheel is 550 feet tall with a diameter of 520 feet, find an equation to describe the shape of the Ferris wheel if we assume the center of the wheel is along the -axis 4 .
::4. 世界上最高的Ferris轮是拉斯维加斯的高滚轮,如果Ferris轮长550英尺,直径为520英尺,那么,如果我们假设方向盘的中心是Y轴,那么,找到一个方程来描述Ferris轮的形状。5. A student says the center of the circle is . Is this correct? Why or why not?
::5. 学生说圆圈的中心(x+4) 2 + (y - 3) 2 = 25 是 (4, 3) 。这是否正确?为什么或为什么不正确?
-
A line segment that has endpoints on the circle is called a
chord
.