课程： 13.4几何序列 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节几何序列

折叠展开
几何序列
The maximum height of a bouncing ball on each bounce is $\begin{aligned} \frac{2}{3} \end{aligned}$ the height of the previous bounce. Say we want to find the height of the ball on the 5th bounce.
::弹跳球每弹跳的最大高度是前一次弹跳的高度为 23 。说我们要在第 5 弹跳时找到球的高度。

A like this is a geometric sequence, and we consider these in this section.
::像这样的几何序列, 我们在本节中考虑这些。

G eometric Sequences
::几何序列

A geometric sequence is a sequence in which the ratio between any two consecutive terms, $\begin{aligned} \frac{a_{n}}{a_{n - 1}}, \end{aligned}$ is constant. This constant value is called the common ratio , and is usually denoted by $\begin{aligned} r \end{aligned}$ . Another way to think of a geometric sequence is that each term is a constant multiple of the next term.
::几何序列是一个序列, 任何两个连续任期( anan-1) 之间的比率都是恒定的。这个恒定值被称为共同比率, 通常由 r 表示。设想几何序列的另一种方式是, 每个术语都是下一个任期的常数倍数。

Example 1
::例1

Consider the sequence $\begin{aligned} 2, 6, 18, 54, \dots \end{aligned}$ Is this sequence geometric? If so, what is the common ratio?
::考虑顺序 2,6,18,54,......这是几何序列吗?如果是,共同比率是多少?

Solution: If we look at each pair of successive terms and evaluate the ratios, we get $\begin{aligned} \frac{6}{2} = \frac{18}{6} = \frac{54}{18} = 3, \end{aligned}$ which indicates that the sequence is geometric and the common ratio is 3.
::解决方案:如果我们看一对相继条款并评估比率,我们就会得到62=186=5418=3,这表明顺序是几何,共同比率是3。

Example 2
::例2

Identify which of the sequences below are geometric. If the sequence is geometric, find the common ratio.
::标明下面的序列是几何。如果序列是几何, 请找到共同比例。

a. $\begin{aligned} 5, 10, 15, 20, \dots \end{aligned}$
::a. 5,10,15,20,...

b. $\begin{aligned} 1, 2, 4, 8, \dots \end{aligned}$
::b. 1,2,4,4,8,...

c. $\begin{aligned} 343, 49, 7, 1, \dots \end{aligned}$
::c. 343,49,7,1,...

Solution:
::解决方案 :

a. This is an arithmetic sequence. The common ratio is 5.
::a. 这是一个算术序列,共同比率为5。

b. Each term in this sequence is 2 times the previous term. This sequence is geometric and $\begin{aligned} r = 2 \end{aligned}$ .
::b. 此序列中每个术语是上一个术语的2倍。该序列是几何和r=2。

c. Each term in this sequence is $\begin{aligned} \frac{1}{7} \end{aligned}$ of the previous term. This sequence is geometric and $\begin{aligned} r = \frac{1}{7} \end{aligned}$ .
::c. 这一顺序中的每个术语为上一个术语的17个,该顺序是几何和r=17。

by CK-12 covers how to identify geometric sequences.
::CK-12涵盖如何识别几何序列。

Now let's see if we can develop a general rule ( $\begin{aligned} n^{t h} \end{aligned}$ term) for the sequence in Example 1. Since we know that each term is multiplied by 3 to get the next term, let's rewrite each term as a product and see if there is a pattern.
::现在让我们看看我们能否为例1的顺序制定一条通则(nth term), 因为知道每个术语乘以3才能获得下一个术语, 让我们重写每个术语作为产品, 看看是否有模式。

$\begin{aligned} a_{1} & = 2 \\ a_{2} & = a_{1} (3) = 2 (3) = 2 (3)^{1} \\ a_{3} & = a_{2} (3) = 2 (3) (3) = 2 (3)^{2} \\ a_{4} & = a_{3} (3) = 2 (3) (3) (3) = 2 (3)^{3} \end{aligned}$

::a1=2a2=a1(3)=2(3)=2(3)(3)=2(3)1a3=a2(3)=2(3)=2(3)=2(3)(3)=2(3)(3)=2(3)=3(3)=3(3)=2(3)(3)=3(3)=3(3)=2(3)=3

This illustrates that the general rule is $\begin{aligned} a_{n} = a_{1} r^{n - 1} \end{aligned}$ , where $\begin{aligned} r \end{aligned}$ is the common ratio. This even works for the 1st term, since $\begin{aligned} a_{1} = 2 (3)^{0} = 2 (1) = 2 \end{aligned}$ .
::这说明一般规则是 an=a1rn-1,r为共同比率。这甚至适用于第一学期,因为 a1=2(3)0=2(1)=2。

Formula for the nth Term of a Geometric Sequence
::几何序列 nth 术语公式

The nth term of a geometric sequence is given by
$\begin{aligned} a_{n} = a_{1} r^{n - 1}, \end{aligned}$
where $\begin{aligned} a_{1} \end{aligned}$ is the 1st term and $\begin{aligned} r \end{aligned}$ is the common ratio.

Example 3
::例3

Write a general rule for the geometric sequence $\begin{aligned} 64, 32, 16, 8, \dots \end{aligned}$
::写出几何序列64,32,16,8的一般规则...

Solution: W e need to know the 1st term and the common ratio to write the general rule. The 1st term is 64, and we can find the common ratio by dividing a pair of successive terms, $\begin{aligned} \frac{32}{64} = \frac{1}{2} \end{aligned}$ . The $\begin{aligned} n^{t h} \end{aligned}$ term rule is thus $\begin{aligned} a_{n} = 64 {(\frac{1}{2})}^{n - 1} \end{aligned}$ .
::解决方案: 我们需要知道第一个学期和共同比率来写通则。第一个学期为64, 我们可以通过分一个连续学期, 3264=12, 找到共同比率。因此, n学期规则是 an=64( 12)n-1。

Example 4
::例4

Find the general rule and the $\begin{aligned} 20^{t h} \end{aligned}$ term for the sequence $\begin{aligned} 3, 6, 12, 24, \dots \end{aligned}$
::找到3,6,12,24的顺序的一般规则和第20个学期...

Solution: The 1st term is 3 and the common ratio is $\begin{aligned} r = \frac{6}{3} = 2, \end{aligned}$ so $\begin{aligned} a_{n} = 3 (2)^{n - 1} \end{aligned}$ . The $\begin{aligned} 20^{t h} \end{aligned}$ term is $\begin{aligned} a_{20} = 3 (2)^{19} = 1, 572, 864. \end{aligned}$
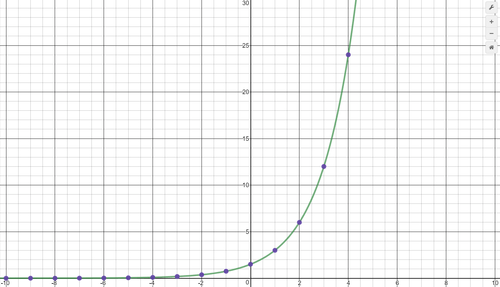
::解答:第一个学期为3个学期,共同比率为r=63=2,因此a=3(2)n-1。第20学期为a20=3(2)19=1,572,864。

Notice that if we plot the terms of a geometric sequence and connect them, the graph looks similar to an exponential function. If we graph the formula $\begin{aligned} a_{n} = 3 (2)^{n - 1} \end{aligned}$ as a function, and plot points for the terms of the sequence, we get the graph below. The points that represent the terms of the sequence are all points that are on the graph of an exponential function.
::请注意,如果我们绘制几何序列的术语并将其连接起来,图形看起来与指数函数相似。如果我们将公式 an=3(2)n-1 作为一个函数和序列条件的绘图点绘制出来,我们就会得到下图。代表序列条件的点是指数函数图形上的所有点。

Example 5
::例5

The maximum height of a bouncing ball is 9 feet. If each subsequent bounce is $\begin{aligned} \frac{2}{3} \end{aligned}$ the height of the previous bounce, find the height of the ball on the 5th bounce.
::弹跳球的最大高度为9英尺。如果随后每次弹跳为23英尺,则在第5次弹跳时找到球的高度。

Solution: Since the height of the ball decreases by the same factor on each bounce, the heights of the bounces are a geometric sequence. We need to write the formula for this sequence. The 1st term is 9, and the common ratio is given as $\begin{aligned} \frac{2}{3} . \end{aligned}$
::解答: 球的高度每反弹会降低同样的因数, 反弹的高度是几何序列。我们需要为此序列写出公式。第一个学期是 9, 共同比率为 23 。

The formula for this sequence is $\begin{aligned} a_{n} = 9 (\frac{2}{3})^{n - 1} . \end{aligned}$
::此序列的公式为=9(23)n-1。

We want to know the height of the ball on the 5th bounce: $\begin{aligned} a_{5} = 9 (\frac{2}{3})^{5 - 1} = 9 (\frac{16}{81}) = \frac{16}{9} = 1 \frac{7}{9} \end{aligned}$ feet.
::我们想知道第5次反弹球的高度:a5=9(233)5-1=9(1681)=169=179英尺。

by DrPhilClark presents a problem similar to the one in Example 5.
::由PhilClark博士撰写, 提出了一个与例5相似的问题。

Example 6
::例6

Find the value of a 10-year-old car if the purchase price was $22,000, and it depreciates at a rate of 9% per year.
::如果购买价为22,000美元,并且每年以9%的折旧率贬值,那么就能找到一辆10岁汽车的价值。

Solution: The 1st term (value of the car after 0 years) is $22,000. The common ratio is $\begin{aligned} 1 - .09 \end{aligned}$ or $\begin{aligned} 0.91 \end{aligned}$ . The value of the car after $\begin{aligned} n \end{aligned}$ years can be determined by $\begin{aligned} a_{n} = 22, 000 (0.91)^{n} . \end{aligned}$ For 10 years, we get $\begin{aligned} a_{10} = 22, 000 (0.91)^{10} = 8, 567.154599 \approx $ 8, 567. \end{aligned}$
::解决方案:第一个学期(汽车在0年后的价值)为22,000美元,共同比率为1-.09或0.91,零年之后的汽车价值由 =22,000(0.91)n确定,10=22,000(0.91)10=8,567.154599=8,567.1599=567美元。

We can use the general rule for the $\begin{aligned} n^{t h} \end{aligned}$ term in a geometric sequence and the given term(s) to determine the 1st term, and write a general rule to find any other term.
::我们可以在几何序列中用nth术语的一般规则和给定术语来确定第一个术语,并写出一条一般规则来找到任何其他术语。

Example 7
::例7

Consider the geometric sequence in which the common ratio is $\begin{aligned} - \frac{4}{5} \end{aligned}$ and $\begin{aligned} a_{5} = 1, 280 \end{aligned}$ . Find the 1st term in the sequence, and write the general rule for the sequence.
::考虑共同比率为 - 45 和 a5= 1,280 的几何序列。在序列中查找第一个词, 并写入序列的一般规则。

Solution: We will start by using the term we know, the common ratio and the general rule, $\begin{aligned} a_{n} = a_{1} r^{n - 1} \end{aligned}$ . By plugging in the values we know, we can then solve for the 1st term, $\begin{aligned} a_{1} \end{aligned}$ .
::解决方案:我们首先使用我们所知道的术语,共同比率和一般规则, an=a1rn-1。通过插入我们所知道的值, 我们可以解决第一个术语,a1。

$\begin{aligned} a_{5} & = a_{1} {(- \frac{4}{5})}^{4} \\ 1, 280 & = a_{1} {(- \frac{4}{5})}^{4} \\ \frac{1, 280}{{(- \frac{4}{5})}^{4}} & = a_{1} \\ 3, 125 & = a_{1} \end{aligned}$

::a5=a1(-45)41 280=a1(-45)41 280(-45)4=a13,125=a1

Now, the $\begin{aligned} n^{t h} \end{aligned}$ term rule is $\begin{aligned} a_{n} = 3, 125 {(- \frac{4}{5})}^{n - 1} \end{aligned}$ .
::现在,第 n 术语规则是 =3,125(- 45n- 1) 。

Example 8
::例8

Find the $\begin{aligned} n^{t h} \end{aligned}$ term rule for a sequence in which $\begin{aligned} a_{1} = 16 \end{aligned}$ and $\begin{aligned} a_{7} = \frac{1}{4} \end{aligned}$ .
::为 a1=16 和 a7=14 的序列查找 nth 术语规则。

Solution: Since $\begin{aligned} a_{7} = \frac{1}{4} \end{aligned}$ and we know the 1st term, we can write the equation $\begin{aligned} \frac{1}{4} = 16 r^{6} \end{aligned}$ and solve for the common ratio:
::解答:自从A7=14和我们知道第一个学期, 我们可以写14=16r6的方程式, 并解决共同比率:

$\begin{aligned} \frac{1}{4} & = 16 r^{6} \\ \frac{1}{64} & = r^{6} \\ \sqrt[6]{\frac{1}{64}} & = \sqrt[6]{r^{6}} \\ \frac{1}{2} & = r \end{aligned}$

::14=16r6164=r61646=r6612=r

The $\begin{aligned} n^{t h} \end{aligned}$ term rule is $\begin{aligned} a_{n} = 16 {(\frac{1}{2})}^{n - 1} . \end{aligned}$
::nth 术语规则是 an=16 (12)n- 1 。

by Mathispower4u reviews the concepts in this section.
::由 Mathispower4u 审查本节的概念。

Example 9
::例9

Find the $\begin{aligned} n^{t h} \end{aligned}$ term rule for the geometric sequence in which $\begin{aligned} a_{5} = 6 \end{aligned}$ and $\begin{aligned} a_{13} = 1, 536 \end{aligned}$ .
::查找 a5=6 和 a13=1,536 的几何序列的 nth 术语规则。

Solution: This time we have two unknowns, the 1st term and the common ratio. We will need to solve a system of equations using both given terms.
::解答: 这次我们有两个未知数, 第一个术语和共同比率。我们需要用两个给定的术语解决一个方程式系统。

Equation 1: $\begin{aligned} a_{5} = 6 \end{aligned}$ , so $\begin{aligned} 6 = a_{1} r^{4} \end{aligned}$ , and solving for $\begin{aligned} a_{1} \end{aligned}$ we get $\begin{aligned} a_{1} = \frac{6}{r^{4}} . \end{aligned}$
::等式 1: a5=6, 所以 6 = a1r4, 和解答 a1, 我们得到 a1=6r4。

Equation 2: $\begin{aligned} a_{13} = 1536 \end{aligned}$ , so $\begin{aligned} 1536 = a_{1} r^{12} \end{aligned}$ , and solving for $\begin{aligned} a_{1} \end{aligned}$ we get $\begin{aligned} a_{1} = \frac{1, 536}{r^{12}} \end{aligned}$ .
::等式2: a13=1536, So 1536=a1r12, 等式2: a13=1536, 所以1536=a1r12, 等式1的解答我们得到a1=1,536r12。

Now that both equations are solved for $\begin{aligned} a_{1}, \end{aligned}$ we can set them equal to each other and solve for $\begin{aligned} r \end{aligned}$ .
::现在两个方程式都为A1解决了, 我们可以把它们等同起来, 并解决r。

$\begin{aligned} \frac{6}{r^{4}} & = \frac{1, 536}{r^{12}} \\ 6 r^{12} & = 1, 536 r^{4} \\ \frac{6 r^{12}}{6 r^{4}} & = \frac{1, 536 r^{4}}{6 r^{4}} & (*) \\ r^{8} & = 256 \\ \sqrt[8]{r^{8}} & = \sqrt[8]{256} \\ r & = 2 \end{aligned}$

::6r4=1,536r126r12=1,536r46r126r4=1,536r46r4(*)r8=2568r=2

Now use $\begin{aligned} r \end{aligned}$ to find $\begin{aligned} a_{1} \end{aligned}$ : $\begin{aligned} a_{1} = \frac{6}{(2^{4})} = \frac{6}{16} = \frac{3}{8} . \end{aligned}$
::现在使用 r 查找 a1: a1=6( 24)=616=38 。

The $\begin{aligned} n^{t h} \end{aligned}$ term rule is $\begin{aligned} a_{n} = (\frac{3}{8}) (2)^{n - 1} \end{aligned}$ .
::Nth术语规则是 an=(38)(2)n-1。

$\begin{aligned} ^{*} \end{aligned}$ Note: In solving the equation above for $\begin{aligned} r, \end{aligned}$ we divided both sides by $\begin{aligned} r^{4} \end{aligned}$ . In general, we cannot divide both sides of an equation by a variable because the variable may equal 0. However, in this case, $\begin{aligned} r \neq 0 \end{aligned}$ since it is the common ratio in a geometric sequence.
::* 注:在解决r的上述方程时,我们将两边除以r4。一般而言,由于变量可能等于0,因此不能将方程的两边除以变量。然而,在本案中,r0,因为它是几何序列中的共同比率。

Feature: Giving Credit
::特点:给予信贷

by Deirdre Mundy
::由Deirdre Mundy 编辑

Each year, credit card debt traps millions of Americans. Young people, especially those with their 1st job and 1st credit card, are at the greatest risk. How can credit card debt pile up so quickly? Is there any way to protect yourself from credit card debt?
::每年,信用卡债务困扰着数百万美国人。年轻人,特别是那些有第一份工作和第一张信用卡的年轻人,风险最大。信用卡债务怎么能够如此迅速地堆积起来? 有没有办法保护自己免受信用卡债务的困扰?

Compounding Interest
::复合利息

Every credit card offer includes an annual percentage rate (APR). This is the rate of interest you'll have to pay on your credit card debt. In theory, an APR of 20% means that for every $100 you carry on the card, you'll have to pay back $120 at the end of the year. However, credit card companies don't calculate interest due once a year; rather, most companies calculate the interest once a month and roll the interest due into the amount you owe them. The amount of money you owe increases like a geometric sequence. This means that if you owe $100 to the credit card company and don't pay it back, in one month you will owe a total of $101.67, in two months you’ll owe $103.36, in three months you'll owe $105.08…and after 12 months you'll owe $121.93. If the card compounds interest daily, you'll have to pay even more. At first glance, this doesn't seem like a high cost to pay, but the average American carries nearly $8,000 in credit card debt. When they miss a payment, their interest rates rise higher. They can easily become tangled in debts they can't repay, and because of their bad credit, they'll be unable to take out loans to buy cars or houses.
::每个信用卡报价都包括年百分比利率。这是您必须支付信用卡债务的利率。从理论上讲, 20 % 的利率意味着您每携带100美元, 在年底, 您就必须偿还120美元。但是, 信用卡公司不会计算每年到期的利息; 相反, 大多数公司每月计算一次利息, 并将到期的利息计入你所欠的利息。您的欠款额像几何序列一样增加。这意味着, 如果您欠信用卡公司100美元, 而不偿还, 那么在一个月内, 您将总共欠101.67美元, 在两个月内, 您将欠103.36美元。在三个月内, 您将欠105. 08美元。 12个月后, 您将欠12个月利息。如果信用卡公司每天将利息加起来, 您将不得不支付更多利息。乍看, 这似乎不像要支付的高成本, 但是平均的美国信用卡债务是将近8 000美元。当他们拖欠一笔款项时, 他们的利率会上升。他们很容易成为拖欠103.36美元, 。因为他们无法偿还贷款, 因为他们不能购买坏的汽车。

How can you avoid getting trapped in a cycle of credit card debt? If you have a credit card, don't treat it as short-term "money-lender." Pay off your balance on time every month. Save up for big-ticket items. If you can't afford to buy something with cash, don't buy it with your card. Finally, make sure you've paid for housing, food, transportation, and utilities before you splurge on luxuries. Staying out of credit card debt is one of the best steps you can take to protect your future.
::如何避免陷入信用卡债务的循环? 如果你有信用卡, 不要把它当作短期的“ 贷款人 ” 。每月按时付清你的余额。储蓄大卡项目。如果您买不起现金购买的东西, 不要用卡买它。最后, 确定您已经支付了住房、食品、交通和水电费, 然后再挤进奢侈品。摆脱信用卡债务是您为保护未来可以采取的最好措施之一。

by BeatTheBush discusses staying out of credit card debt.
::BeatTheBush讨论如何摆脱信用卡债务,

Summary
::摘要

A geometric sequence is a sequence in which the ratio between any two consecutive terms, $\begin{aligned} \frac{a_{n}}{a_{n - 1}} \end{aligned}$ , is constant. This constant value is called the common ratio.
::几何序列是连续两个任期(anan-1)之间的比率不变的序列。这个不变值被称为共同比率。

The formula for the nth term of a geometric sequence is $\begin{aligned} a_{n} = a_{1} r^{n - 1}, \end{aligned}$ where $\begin{aligned} a_{1} \end{aligned}$ is the 1st term and $\begin{aligned} r \end{aligned}$ is the common ratio.
::几何序列 n 的公式是 an=a1rn-1, 其中 a1 是第一个条件, r 是共同比率。

Review
::回顾

Identify which of the following sequences are arithmetic, geometric, or neither:
::标明下列哪些序列是算术、几何或两者兼有:

1. $\begin{aligned} 2, 4, 6, 8, \dots \end{aligned}$

2. $\begin{aligned} \frac{1}{2}, \frac{3}{2}, \frac{9}{2}, \frac{27}{2}, \dots \end{aligned}$

3. $\begin{aligned} 1, 2, 4, 7, \dots \end{aligned}$

4. $\begin{aligned} 24, - 16, \frac{32}{3}, - \frac{64}{9}, \dots \end{aligned}$

5. $\begin{aligned} 10, 5, 0, - 5, \dots \end{aligned}$

6. $\begin{aligned} 3, 4, 7, 11, \dots \end{aligned}$

Given the 1st term and common ratio, write the $\begin{aligned} n^{t h} \end{aligned}$ term rule and find the 1st five terms in each sequence.
::考虑到第一个任期和共同比率, 写下N组任期规则, 并在每个序列中找到前五个任期。

7. $\begin{aligned} a_{1} = 32 \end{aligned}$ and $\begin{aligned} r = \frac{3}{2} \end{aligned}$
::7.a1=32和r=32

8. $\begin{aligned} a_{1} = - 81 \end{aligned}$ and $\begin{aligned} r = - \frac{1}{3} \end{aligned}$
::8.a1=-81和r=-13

9. $\begin{aligned} a_{1} = 7 \end{aligned}$ and $\begin{aligned} r = 2 \end{aligned}$
::9.1=7和r=2

10. $\begin{aligned} a_{1} = \frac{8}{125} \end{aligned}$ and $\begin{aligned} r = - \frac{5}{2} \end{aligned}$
::10.1=8125和r=-52

Find the $\begin{aligned} n^{t h} \end{aligned}$ term rule for each of the following geometric sequences:
::为以下几何序列中的每一序列查找 nth 术语规则 :

11. $\begin{aligned} 162, 108, 72, \dots \end{aligned}$

12. $\begin{aligned} - 625, - 375, - 225, \dots \end{aligned}$

13. $\begin{aligned} \frac{9}{4}, - \frac{3}{2}, 1, \dots \end{aligned}$

14. $\begin{aligned} 3, 15, 75, \dots \end{aligned}$

15. $\begin{aligned} 5, 10, 20, \dots \end{aligned}$

16. $\begin{aligned} \frac{1}{2}, - 2, 8, \dots \end{aligned}$

Use the given information to find the $\begin{aligned} n^{t h} \end{aligned}$ term rule for each geometric sequence.
::使用给定信息为每个几何序列查找 nth 术语规则。

17. $\begin{aligned} r = \frac{2}{3} \end{aligned}$ and $\begin{aligned} a_{8} = \frac{256}{81} \end{aligned}$
::17 r = 23 和 a8 = 25681

18. $\begin{aligned} r = - \frac{3}{4} \end{aligned}$ and $\begin{aligned} a_{5} = \frac{405}{8} \end{aligned}$
::18 r=-34和a5=4058

19. $\begin{aligned} r = \frac{6}{5} \end{aligned}$ and $\begin{aligned} a_{4} = 3 \end{aligned}$
::19.r=65和A4=3

20. $\begin{aligned} r = - \frac{1}{2} \end{aligned}$ and $\begin{aligned} a_{7} = 5 \end{aligned}$
::20 r= 12和a7=5

21. $\begin{aligned} r = \frac{6}{7} \end{aligned}$ and $\begin{aligned} a_{0} = 1 \end{aligned}$
::21 r= 67 和 a0= 1

22. $\begin{aligned} a_{1} = \frac{11}{8} \end{aligned}$ and $\begin{aligned} a_{7} = 88 \end{aligned}$
::22.1=118和A7=88

23. $\begin{aligned} a_{1} = 24 \end{aligned}$ and $\begin{aligned} a_{4} = 81 \end{aligned}$
::a231=24和a4=81

24. $\begin{aligned} a_{1} = \frac{343}{216} \end{aligned}$ and $\begin{aligned} a_{5} = \frac{6}{7} \end{aligned}$
::24.1=343216和a5=67

25. $\begin{aligned} a_{6} = 486 \end{aligned}$ and $\begin{aligned} a_{10} = 39, 366 \end{aligned}$
::a25.6=486和a10=39 366

26. $\begin{aligned} a_{5} = 648 \end{aligned}$ and $\begin{aligned} a_{10} = \frac{19, 683}{4} \end{aligned}$
::a5=648和a10=19 6834

27. $\begin{aligned} a_{3} = \frac{2}{3} \end{aligned}$ and $\begin{aligned} a_{5} = \frac{3}{2} \end{aligned}$
::27.3=23和5=32

28. $\begin{aligned} a_{5} = \frac{4}{3} \end{aligned}$ and $\begin{aligned} a_{10} = - \frac{128}{3} \end{aligned}$
::28.5=43和10=1283

Explore More
::探索更多

1. Rebecca inherited some land worth $50,000 that has increased in value by an average of 5% per year for the last 5 years. If this rate of appreciation continues, about how much will the land be worth in another 10 years?
::1. Rebecca继承了价值50 000美元的一些土地,在过去5年中,土地价值平均每年增加5%,如果这一升值率继续下去,关于今后10年土地价值多少?

2. A farmer buys a new tractor for $75,000. If the tractor depreciates in value by about 6% per year, how much will it be worth after 15 years?
::2. 农民以75 000美元购买一辆新的拖拉机,如果拖拉机每年贬值约6%,15年后价值多少?

3. The sequence below shows the distance (in centimeters) that a pendulum travels with each successive swing. Write a general rule for the geometric sequence.
::3. 下面的顺序显示一个钟摆每连续摆动的距离(以厘米计),为几何顺序写出一条通则。

80, 72, 64.8, 58.32, ...

4. A bacteria sample doubles every hour. After four hours, there are 64 bacteria in the sample. What is the $\begin{aligned} n^{t h} \end{aligned}$ term rule for the geometric sequence represented by this situation?
::4. 细菌样本每小时翻一番,经过四个小时后,样本中有64种细菌。

5. Ricardo wants to have $100,000 saved up to pay for college by the time his son graduates from high school 16 years from now. If he chooses an investment vehicle that claims to yield 7% growth per year, how much should he invest today? Give your answer to the nearest $1,000.
::5. Ricardo想在16年后他的儿子从高中毕业时节省10万美元,以支付大学费用,如果他选择了一种投资工具,声称每年增长7%,那么今天他应该投资多少?你回答最近的1000美元。

6. If a piece of machinery depreciates (loses value) at a rate of 6% per year, what was its initial value if it is 10 years old and worth $50,000? Give your answer to the nearest $1,000.
::6. 如果一台机械每年以6%的速率折旧(损益),如果其最初价值为10年,价值为50 000美元,那么其最初价值是什么?回答最接近的1 000美元。

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try the interactives below to reinforce the concepts explored in this section:
::尝试下面的交互作用来强化本节所探讨的概念:

章节大纲

常规

几何序列

G eometric Sequences ::几何序列

Example 1 ::例1

Example 2 ::例2

Formula for the nth Term of a Geometric Sequence ::几何序列 nth 术语公式

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Example 9 ::例9

Feature: Giving Credit ::特点:给予信贷

Compounding Interest ::复合利息

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

G eometric Sequences
::几何序列

Example 1
::例1

Example 2
::例2

Formula for the nth Term of a Geometric Sequence
::几何序列 nth 术语公式

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Example 8
::例8

Example 9
::例9

Feature: Giving Credit
::特点:给予信贷

Compounding Interest
::复合利息

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX