14.9 答复-第9章:合理功能
章节大纲
-
Section 9.2 Simplifying Rational Expressions
::第9.2节 简化合理表达式Review
::回顾-
4
x
2
2
x
+
3
::422x+3 -
(
x
+
2
)
x
(
x
+
5
)
:x+2)xx(x+5)
-
(
x
−
3
)
(
x
−
4
)
: -
(
x
+
7
)
x
(
x
−
7
)
: -
-
2
(
2
x
+
1
)
(
2
x
+
3
)
::-2(2x+1)(2x+3) -
2
(
x
−
4
)
3
(
x
+
1
)
(
x
−
1
)
::2(x-4)3(x+1)(x-1) -
(
3
x
+
4
)
(
3
x
+
1
)
: -
(
x
+
2
)
x
: -
x
(
x
+
3
)
(
2
x
−
7
)
4
(
x
−
7
)
: -
x
−
2
::x-2 -
(
3
x
−
1
)
(
x
2
+
1
)
: -
(
x
+
3
)
(
2
x
+
5
)
:
Explore More
::探索更多-
No, they are not the same, because
x
−
2
x
−
3
is in simplest form.
5
x
10
x
can be reduced using division rules, so it does simplify to
1
2
.
::不,它们不同,因为 x-2x-3 的形式最简单。 5x10x 可以通过分法规则减少,因此简化为12。 -
Width: Perimeter = 1:6
::宽度:周边=1:6 -
Base: Perimeter = 2:5
::基数:周边=2:5 -
2
(
x
+
1
)
(
x
−
1
)
=
2
x
2
−
2
::2(x+1)(x-1)=2x2-2 -
You can't cancel the
x
2
;
you have to factor the polynomials before simplifying.
::您无法取消 x2 ; 在简化前, 您必须先将多义因素考虑在内 。
Section 9.3 Multiplying and Dividing Rational Expressions
::第9.3节 乘数和分裂性合理表达式Review
::回顾-
x
5
y
8
::x5y8 -
x
2
+
5
x
−
3
2
x
2
−
3
x
+
1
::x2+5x - 32x2 - 3x+1 -
2
(
x
2
+
14
x
−
15
)
(
8
x
2
−
18
x
+
9
)
::2(x2+14x-15)(8x2-18x+9) -
2
x
−
3
x
−
3
::2 - 3x-3 - 3 -
8
y
z
5
7
x
::8yz57x 8yz57x -
x
(
x
2
+
6
x
+
2
)
-
3
(
6
x
2
−
13
x
−
5
)
::x(x2+6x+2)-3(6x2-13x-5) -
x
(
x
+
2
)
(
x
+
3
)
::x( xx+2)( x+3) -
(
x
+
5
)
(
5
x
+
3
)
: -
2
3
x
(
x
−
3
)
::23x(x-3) -
x
5
(
x
+
3
)
::x5( x+3 ) -
3
(
2
x
−
5
)
2
::3(2x-5)2 -
-
1
x
−
1
::-1x-1 -
(
2
x
2
−
3
x
−
12
)
(
x
−
3
)
3
(
x
2
+
4
x
−
7
)
: -
2
(
x
2
+
2
x
+
15
)
(
8
x
2
−
3
x
+
15
)
::2(x2+2x+15)(8x2-3x+15) -
(
x
+
1
)
(
4
x
2
+
5
x
−
8
)
(
x
+
2
)
(
−
x
2
+
6
x
+
1
)
:
Explore More
::探索更多-
Error is that 4 and x are not common factors. The correct answer is
(
x
+
4
)
(
x
−
4
)
(
x
−
4
)
=
(
x
+
4
)
.
::错误是 4 和 x 不是常见系数。 正确的答案是 (x+4)(x-4)(x-4)(x-4) = (x+4) = (x+4)。 -
R
1
=
R
2
R
T
O
T
R
2
−
R
T
O
T
;
R
2
=
R
1
R
T
O
T
R
1
−
R
T
O
T
::R1=R2RTOTR2-RTOT;R2=R1RTOTR1-RTOT -
x
−
1
x
+
4
::x-1x+4 x-1x+4 -
1. False, you add the exponents. 2.True. 3. True. 4. False. The answer is
x
2
+
4
x
+
4
.
::1. 假,您添加前言。 2. true. 3. true. 4. false, 答案为 x2+4x+4。 -
a.
3
y
10
x
b.
6
z
4
5
y
2
c.
1
x
(
x
−
1
)
::a. 3y10x b. 6z45y2 c. 1x(x-1) -
No. To get the same answer, you need to have
1
÷
1
2
÷
6
.
::不,要得到同样的答案,你需要 1126。 -
1.
2
+
1
1
+
1
2
+
2
4
+
4
5
;
2
+
1
1
+
1
2
+
2
5
+
5
6
.
2.
2.667
,
2.723
,
2.717
,
2.707
,
2.700.
3. As the number of terms increases, the number comes close to 2.7. 4.
2
+
1
1
+
1
2
+
2
6
+
6
7
. Yes, the decimal value is 2.696.
::1. 2+11+12+12+24+45;2+11+12+12+25+56。 2.2.667、2.723、2.717、2.707、2.700。 3. 随着用语数目的增加,数目接近2.7.4. 2+11+12+12+26+67。是,小数点值为2.696。
Section 9.4 Adding and Subtracting Rational Expressions with Like Denominators
::第9.4节 添加和减减与类似引号相同的逻辑表达式Review
::回顾-
7
x
::7x 7x -
6
x
::6x 6x -
9
−
2
x
5
x
::9-2x5x -
4
+
x
x
::4+xxx 4+xx - 1
-
x
+
5
x
−
2
::x+5x-2 - 4
-
5
x
+
11
(
x
−
5
)
(
x
+
1
)
::5x+11(x-5)(x+1) -
3
x
+
2
::3x+2 3x+2 -
x
2
+
2
x
+
4
x
3
−
8
::x2+2x+4x3-8 -
2
(
x
+
1
)
x
2
+
1
::2(x+1)x2+1 -
20
x
2
−
20
x
−
7
(
2
x
+
1
)
(
2
x
−
3
)
(
2
x
+
3
)
::20x2-20x-7(2x+1)(2x-3)(2x+3) -
3
(
x
2
−
2
x
−
12
)
(
x
+
4
)
(
x
−
4
)
(
x
−
2
)
::3(x2-2x-12)(x+4)(x-4)(x-2)
Explore More
::探索更多-
You need a common denominator of 15.
::你需要一个共同的15分之一的分母。 -
When simplifying in the 1st step, there should be a +
x
in the numerator, not a -
x
.
::当第1步简化时,分子中应有一个+x,而不是一个 -x。 -
When simplifying in the 1st step, you should have
2
x
2
+
8
x
in the numerator.
::在第一步简化时,分子中应包含 2x2+8x 。 -
9 feet
::9英尺9英尺 -
x
=
6
5
;
y
=
3
20
::x=65;y=320 -
2
x
+
5
x
+
2
::2x+5x+2
Section 9.5 Adding and Subtracting Rational Expressions with Unlike Denominators
::第9.5节 增加和减减与不同控号的逻辑表达式Review
::回顾-
x
−
3
::x-33 个 -
No LCD
::无液晶 -
7
4
x
::74x 74x -
x
2
+
3
x
−
1
x
(
x
+
3
)
::x2+3x- 1x( x+3) -
(
x
+
10
)
(
x
−
1
)
4
x
(
x
+
2
)
: -
5
x
+
2
::5x+2 5x+2 -
-
1
(
x
−
50
2
x
2
−
7
x
−
15
::-1(x- 502x2-7x-15) -
2
(
5
x
−
9
)
(
x
+
2
)
(
3
x
−
5
)
::2(5x-9)(x+2)(3x-5) -
(
x
−
3
)
2
(
2
x
−
3
)
: -
3
x
−
3
::3x-3 -
4
x
+
3
::4x+3 4x+3 -
2
(
2
x
2
+
5
x
+
6
)
(
x
+
5
)
(
x
+
2
)
(
x
+
3
)
::2( 2x2+5x+6)(x+5)(x+2)(x+3) -
x
2
+
30
x
+
23
x
(
x
−
2
)
(
3
x
+
5
)
::x2+30x+23x(x-2)(3x+5) -
20
x
2
+
42
x
−
7
5
x
(
x
+
1
)
(
x
−
1
)
::20x2+42x-75x(x+1)(x-1)
Explore More
::探索更多-
You need to use LCD to make the denominators the same.
::您需要使用液晶显示器使分母相同 。 -
5
x
−
1
x
2
−
x
−
2
::5x-1x2-x-2 -
2
x
2
+
22
x
−
33
2
(
x
+
3
)
(
x
−
2
)
::2x2+22x-32(x+3)(x-2)
Section 9.6 Solving Rational Equations Using the Least Common Denominator
::第9.6节 利用最不常见数字符号解决合理等式Review
::回顾-
Yes
::是 是 -
No
::否 无 -
x
=
-
5
;
x
=
2
::x=-5;x=2 -
x
=
-
7
13
::x=-713 x=-713 -
x
=
1
4
::x=14x=14 -
x
=
2
3
::x=23x=23 -
x
=
-
5
;
x
=
2
::x=-5;x=2 -
x
=
3
4
(
5
+
√
17
)
,
-
3
4
(
√
17
−
5
)
::x=34(517),-34(17)-5) -
x
=
-
28
;
x
=
0
::x=- 28;x=0 -
x
=
5
;
x
=
-
3
::x=5;x=3 x=3 -
x
=
-
1
4
::x=-14 -
x
=
-
7
±
√
5
2
::x=-7=52
Explore More
::探索更多-
x
=
2
√
15
15
::x=21515 -
MN=10; YZ = 3
::MN=10;YZ=3 -
360 defective phones
::360台有缺陷电话 -
1,290 students
::1 290名学生 -
1.25 mph
::1.25 百万平方厘米 -
Bus speed = 35mph. Train speed =105 mph.
::班车速度=35米,火车速度=105米。
Section 9.7 Solving Rational Equations Using Cross Multiplication
::第9.7节 利用交叉乘法解决合理等式Review
::回顾-
Yes
::是 是 -
x
=
6
,
x
=
-
2
::x=6,x=2 x=6,x=2 -
x
=
-
5
,
x
=
2
::x=5,x=2 x=5,x=2 -
x
=
6
,
x
=
-
1
::x=6,x=-1 -
x
=
±
1
::x1 -
x
=
-
4
,
x
=
1
2
::x=4,x=12 x=4,x=12 -
x
=
-
3
::x=-3x=3 -
x
=
-
2
,
9
2
::x=-2,92x=-2,92 -
x
=
5
28
::x=528x=528 -
x
=
-
40
::x=-40 -
x
=
8
,
x
=
-
1
::x=8,x=-1
Explore More
::探索更多-
a.
x
≠
±
a
; b.
x
≠
a
::a. xa;b. xa -
x
=
21
::x=21x=21 -
12 pages
::12页 -
25 ounces
::25 盎司 -
20 ounces
::20 盎司 -
160 feet
::160英尺 -
29.75 miles
::29.75英里
Section 9.8 Graphing Rational Functions in Standard Form
::第9.8节 标准表格中的逻辑函数图示Review
::回顾-
x
=
-
8
,
y
=
-
3
::x=8,y=3 x=8,y=3 -
x
=
4
,
y
=
6
::x=4,y=6 x=4,y=6 -
Domain:
{
x
∈
ℜ
:
x
≠
0
}
;
Range:
{
y
∈
ℜ
:
y
≠
0
}
;
Asymptotes:
x
=
0
,
y
=
0
;
No intercepts.
::域 : {xR:x0}; 范围 : {yR:y0}; 微粒: x=0,y=0; 没有拦截 。 -
Domain:
{
x
∈
ℜ
:
x
≠
0
}
;
Range:
{
y
∈
ℜ
:
y
≠
6
}
;
Asymptotes:
x
=
0
,
y
=
6
;
Intercept at
x =
-
1
6
.
::域 : {xR:x0} ; 范围 : {yR:y6} ; 微粒 : x= 0. y=6; 拦截 : x = - 16 。 -
Domain:
{
x
∈
ℜ
:
x
≠
0
}
;
Range:
{
y
∈
ℜ
:
y
≠
0
}
;
Asymptotes:
x
=
0
,
y
=
0
; No intercepts.
::域 : {xR:x0}; 范围 : {yR:y0}; 微粒: x=0,y=0; 没有拦截 。 -
Domain:
{
x
∈
ℜ
:
x
≠
-
3
}
;
Range:
{
y
∈
ℜ
:
y
≠
0
}
;
Asymptotes:
x
=
-
3
,
y
=
0
;
Intercept:
(
0
,
-
1
3
)
.
::域 : {xR:x_ 3}; 范围 :{yR:y0}; 微粒: x= 3,y=0; 拦截: (0, 13) 。 -
Domain:
{
x
∈
ℜ
:
x
≠
-
5
}
;
Range:
{
y
∈
ℜ
:
y
≠
0
}
;
Asymptotes:
x
=
-
5
,
y
=
0
; Intercept:
(
0
,
1
5
)
.
::域 : {xR:x* 5}; 范围 : {yR:y0}; 微粒: x= 5,y=0; 拦截: (0, 15) 。 -
Domain:
{
x
∈
ℜ
:
x
≠
3
}
;
Range:
{
y
∈
ℜ
:
y
≠
-
4
}
;
Asymptotes:
x
=
3
,
y
=
-
4
;
Intercepts:
(
3
1
4
,
0
)
,
(
0
,
-
4
1
3
)
.
::域 : {xR:x3}; 范围 :{yR:y4}; 微粒: x=3,y=4; 截取 : (314,0,413) 。 -
Domain:
{
x
∈
ℜ
:
x
≠
-
4
}
;
Range:
{
y
∈
ℜ
:
y
≠
-
3
}
;
Asymptotes:
x
=
-
4
,
y
=
-
3
;
Intercepts:
(
-
3
1
3
,
0
)
,
(
0
,
-
2
1
2
)
.
::域 : {xR:x_ 4}; 范围 :{yR:y- 3}; 亚星点 : x= 4,y=-3; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
0
}
;
Range:
{
y
∈
ℜ
:
y
≠
2
}
;
Asymptotes:
x
=
0
,
y
=
2
;
Intercept:
(
-
2.5
,
0
)
.
::域 : {xR:x0}; 范围 :{yR:y2}; 微粒: x=0,y=2; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
-
2
}
;
Range:
{
y
∈
ℜ
:
y
≠
3
}
;
Asymptotes:
x
=
-
2
,
y
=
3
;
Intercepts:
(
-
1
2
3
,
0
)
,
(
0
,
5
2
)
.
::域 : {xR:x_2}; 范围 :{yR:y3}; 微粒: x=-2,y=3; 拦截 -
y
=
1
x
−
6
−
4
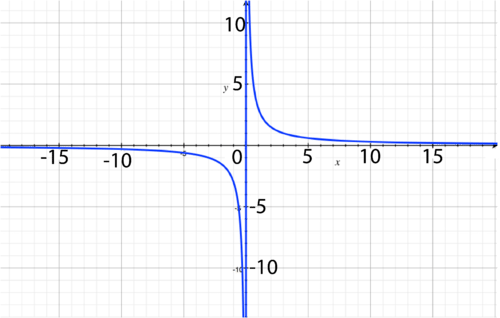
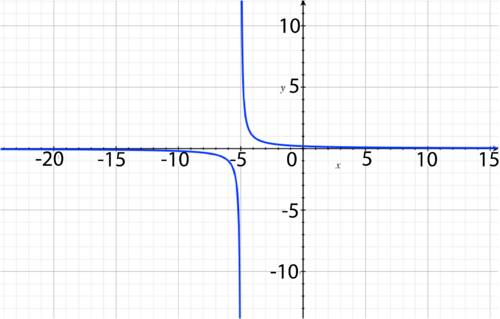
::y=1x-6 - 4 -
y
=
-
1
x
+
1
+
3
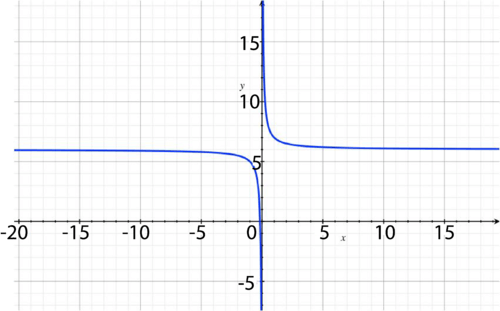
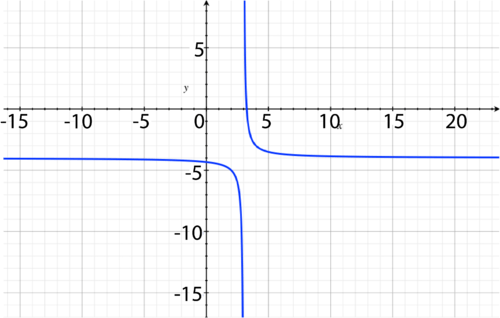
::y=-1x+1+3 y=-1x+1+3
Explore More-
y
=
1
x
−
5
+
3
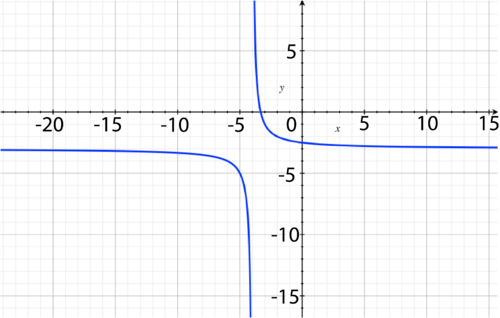
::y=1x-5+3 y=1x-5+3 -
y
=
1
x
+
3
−
2
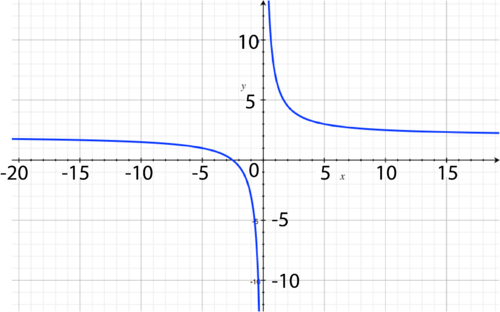
::y=1x+3-2 -
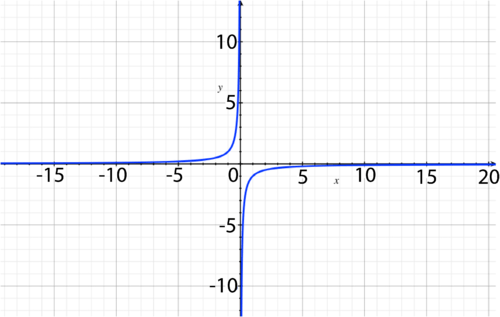
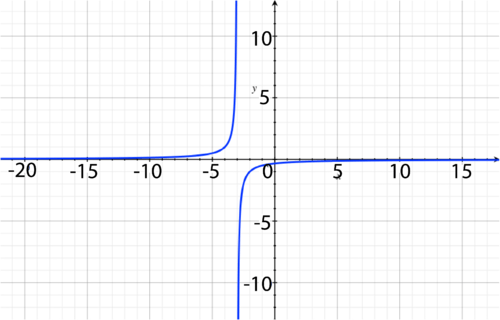
As the volume goes down, the pressure goes up. This shows the inverse proportionality. This graph shows a rational expression with a vertical asymptote at
x
=
0
,
and a horizontal asymptote at
y
=
0
.
::随着音量下降, 压力会上升。 这显示了反比例性。 此图显示了一种合理表达式, 以 x=0 的垂直小数表示, 以 y=0 的横向小数表示 。
Section 9.9 Graphing Other Rational Functions
::第9.9节 其他合理职能图示Review
::回顾-
x
=
-
7
,
y
=
1
::x=-7,y=1 -
x
=
-
2
,
x
=
-
4
,
y
=
0
::x=-2,x=4,y=0 -
x
=
-
5
; oblique asymptote:
y
=
x
−
5
::x= 5; 斜线渐变: y=x- 5 -
x
=
3
; oblique asymptote:
y
=
x
+
3
::x=3; 斜线无症状: y=x+3 -
Domain:
{
x
∈
ℜ
:
x
≠
5
}
;
Range:
{
y
∈
ℜ
:
y
≠
1
}
;
Asymptotes:
x
=
5
,
y
=
1
;
Intercepts:
(
-
3
,
0
)
,
(
0
,
-
3
5
)
;
Holes: none.
::域 : {xR:x5}; 范围 :{yR:y1}; 亚星点 : x=5,y=1; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
-
5
}
;
Range:
{
y
∈
ℜ
:
y
≠
-
1
2
}
;
Asymptotes :
x
=
-
5
,
y
=
-
1
2
;
Intercepts:
(
3
,
0
)
,
(
0
,
3
10
)
;
Holes: none.
::域 : {xR:x* 5}; 范围 :{yR:y* 12}; 微粒 :x= 5,y= 12; 截取 : (3,0,0,310); 空: 无 。 -
Domain:
{
x
∈
ℜ
:
x
≠
−
3
,
x
≠
4
}
;
Range:
y
∈
ℜ; Asymptotes:
x
=
-
3.
x
=
4
,
y
=
0
;
Intercepts:
(
-
1
,
0
)
,
(
0
,
-
1
12
)
;
Holes: none.
::域 : {xR:x3,x4}; 范围 : yR; 亚本托斯: x=-3.x=4,y=0; 截取器 -
Domain:
{
x
∈
ℜ
:
x
≠
-
1.5
,
x
≠
7
}
;
Range:
{
y
∈
ℜ
:
y
≠
0
}
;
Asymptotes:
x
=
-
3
2
,
y
=
0
; Intercepts:
(
0
,
1
3
)
; Holes:
x
=
7
.
::域 : {xR:x- 1.5,x7}; 范围 :{yR:y0}; 亚星点数: x=-32,y=0; 拦截器: (0,13); 空洞: x=7。 -
Domain:
{
x
∈
ℜ
:
x
≠
6
,
x
≠
2
}
;
Range:
{
y
∈
ℜ
:
y
≠
1
}
;
Asymptotes:
x
=
6
,
x
=
2
,
y
=
1
;
Intercepts:
(
-
3
,
0
)
,
(
-
2
,
0
)
,
(
0
,
1
2
)
;
Holes: none.
::域 : {xR:x6,x2}; 范围 :{yR:y1}; 亚辛托斯: x=6,x=2,y=1; 拦截( 3, 3,0, (2,0, 0, 12); 空洞: 无 。 -
Domain:
{
x
∈
ℜ
:
x
≠
−
1.5
,
x
≠
1
}
;
Range:
{
y
∈
ℜ
:
y
≠
1
2
}
;
Asymptotes:
x
=
1
,
x
=
-
3
2
,
y
=
1
2
;
Intercepts:
(
0
,
-
4
3
)
; Holes: none.
::域 : {xR:x1.5,x1}; 范围 :{yR:y12}; 微粒: x=1,x=-32,y=12; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
-
4
3
,
-
2
}
;
Range:
{
y
∈
ℜ
:
y
≠
2
3
}
;
Asymptotes:
x
=
-
4
3
,
y
=
2
3
;
Intercepts:
(
5
2
,
0
)
,
(
0
,
-
5
4
)
;
Holes:
(
-
2
,
9
2
)
.
::域 : {xR:x- 43,-2}; 范围 :{yR:y23}; 微粒: x=-43,y=23; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
-
5
,
x
≠
2
}
;
Range:
{
y
∈
ℜ
:
y
≠
1
}
;
Asymptotes:
x
=
-
5
,
y
=
1
; Intercepts:
(
-
2
,
0
)
,
(
0
,
2
5
)
;
Holes:
(
2
,
4
7
)
.
::域 : {xR:x 5,x2}; 范围 :{yR:y1}; 微粒: x= 5,y=1; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
-
6
}
;
Range:
{
y
∈
ℜ
}
;
Intercepts:
(
5
,
0
)
,
(
0
,
-
5
)
;
Holes:
(
-
6
,
1
)
.
::域 : {xR:x 6}; 范围 :{yR}; 拦截 -
Domain:
{
x
∈
ℜ
:
x
≠
2.
x
≠
3
}
;
Range:
{
y
∈
ℜ
}
;
Asymptotes:
x
=
2
,
x
=
3
,
y
=
x
+
3
; Intercepts:
(
-
1
,
0
)
,
(
0
,
0
)
;
Holes:
(
3
,
12
)
.
::域 : {xR:x2.x3}; 范围 :{yR}; 亚速特: x=2,x=3,y=3,y=x+3; 截取( 1,0,0,0); 空
Explore More-
False, because there could be a hole.
::假的,因为可能有一个洞。 -
False; it will be
y =
0.
::假的;它会是y=0。 -
None, because
x
2
+
2
≠
0
for any
x
.
::无, 因为 x2+2+% 0 代表任何 x 。 -
There is a hole at
x
=
-
5
3
.
::x=-53处有一个洞。 -
Darnell, because
x
4
−
16
=
(
x
−
2
)
(
x
+
2
)
(
x
2
+
4
)
,
the latter of which is never zero.
::达内尔, 因为 x4 - 16=(x-2)(x+2)(x2+4), 后者从不为零 。 -
Zeb
::扎布 -
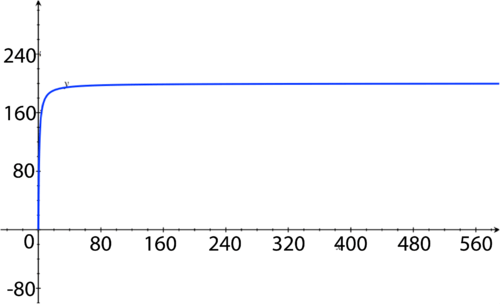
The rabbit population
approaches
a maximum at 200 rabbits.
::兔子数量最多接近200只兔子。 -
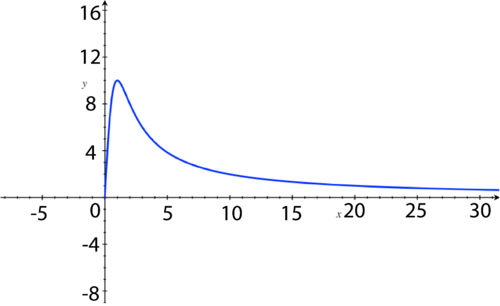
The concentration peaks at
t
=
1
,
then decreases to close to zero, since the horizontal asymptote is
y
=
0
.
::浓度峰值在 t=1 时为峰值,然后降至接近于零,因为水平单点为 y=0 。
Section 9.10 Connections: Getting the Job Done
::第9.10节 连接:完成任务-
Teenager: 5 hours, 20 min. Father: 16 hours.
::青少年:5小时20分钟,父亲:16小时。 -
2 hours, 55 minutes
::2小时55分 -
4 hours, 48 minutes
::4小时48分48分 -
1 hour, 48 minutes
::1小时48分 -
17.14 min
::17.14分钟
Section 9.11 Connections: "Say Cheese," Great Camera Phone Photos
::第9.11节 连接:“说起司”,大相机电话照片-
Answers will vary depending on the phone used.
::答复将因使用的电话而异。 -
Answers will vary depending on the phone used in Question 1.
::答复将因问题1中使用的电话而异。
-
4
x
2
2
x
+
3
