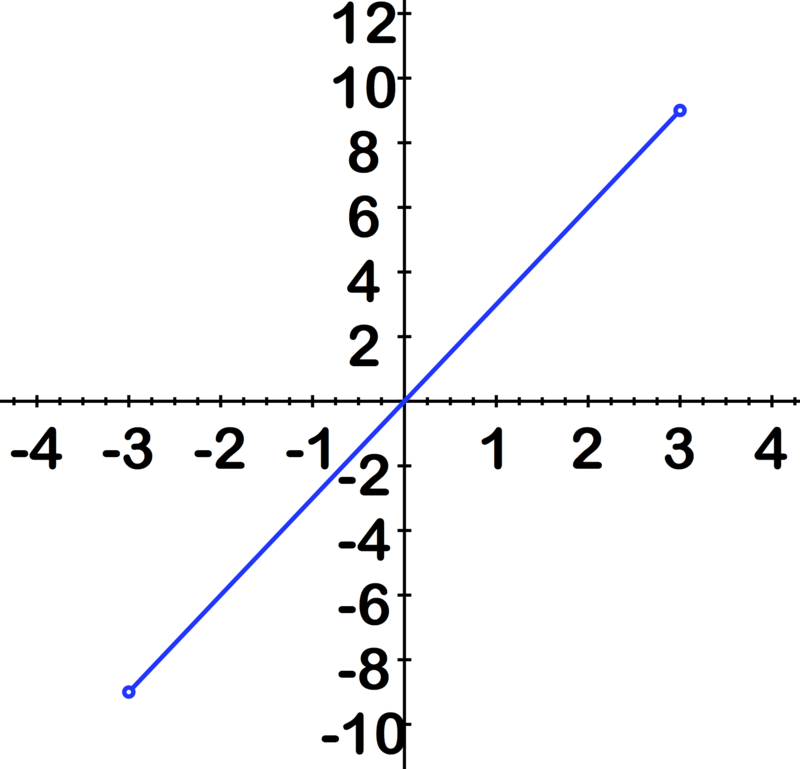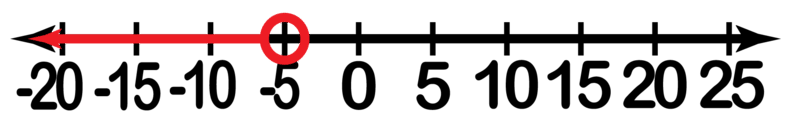课程： 1.14 间和间和间和

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

间距

Introduction
::导言

Suppose you and two friends are out for lunch and you decide to buy tacos.
::假设你和两个朋友出去吃午饭决定买玉米饼

lesson content

Together you have $15 to spend on lunch, and tacos are $1.25 each. It is clear that the total cost could be graphed as a discrete function of the number of tacos purchased, but how would you specify that the graph should not include values greater than $15 or less than $3.75 (one taco each)?
::您共需15美元午餐,而玉米卷每份为1.25美元。成本总额显然可以作为购买玉米卷数量的一个独立函数来计算,但您如何具体说明图表中数值不应大于15美元或小于3.75美元(每张玉米卷)?

Real Values and Intervals
::实际价值和间数

This video provides an overview of how to express a set of real numbers in interval notation, in set notation , and as a graph on a number line:
::本视频概述如何用间距符号、设置符号和数字行上的图表表达一组真实数字:

A function is defined as a real function if both the domain (the $\begin{aligned} x \end{aligned}$ or other input values) and the range (the $\begin{aligned} y \end{aligned}$ or other output valuare sets of real numbers. Many of the functions you have likely encountered before are real functions, and many of these functions have Domain = $\begin{aligned} R \end{aligned}$ . Consider, for example, the function $\begin{aligned} y = 3 x \end{aligned}$ . A section of the graph of this function is shown below:
::如果域名( x 或其他输入值) 和范围( y 或其他输出 valuare 实际数字的 valuare 组) 和范围( y 或其他输出 valuare 组) , 函数就被定义为实际函数。你以前可能遇到的许多函数都是真实函数, 而其中的许多函数是 Domain = R。例如,请考虑 y= 3x 的函数。此函数图图的一节如下:

You may already be familiar with the graphs of lines. And you may be in the habit of placing arrows at the ends. We do this to indicate that the line will continue forever in both positive and negative directions, in terms of both the domain and the range. The line above, however, only shows the function $\begin{aligned} y = 3 x \end{aligned}$ on the interval (-3, 3). The " data-term="Parentheses" role="term" tabindex="0"> parentheses indicate that the graph does not include the endpoints of the interval, where $\begin{aligned} x = - 3 \end{aligned}$ and $\begin{aligned} x = 3 \end{aligned}$ . We call this an open interval . You may have noticed that the open interval notation looks like the notation for a point $\begin{aligned} (x, y) \end{aligned}$ in the plane. It is important to read an example or a homework problem carefully to avoid confusing a point with an interval! The difference is generally quite clear from the context. In contrast, a closed interval does contain its endpoints. We indicate a closed interval with square brackets . For example, [-3, 3] indicates the set of numbers between -3 and 3, including -3 and 3.
::您可能已经熟悉行的图表。您可能习惯于在结尾处放置箭头。我们这样做是为了表明线条会永远以正向和负方向, 包括域和范围。但是, 上面的线条只显示间距( 3, 3) 上的 y= 3x 函数( 3, 3) 。括号显示, 图形不包括间距的端点, 即 x= 3 和 x= 3 。我们称此为开放间隔。您可能注意到, 开放间距的标记看起来像平面上一个点( x, y) 的标记。重要的是要仔细阅读一个示例或功课问题, 以避免与间距混淆某个点。差异通常在上下文中非常清楚。相反, 一个封闭间距包含它的端点。我们用方括号表示一个封闭间距。例如, [ 3, 3 3] 表示数字在 - 3 3 3 和 3 3 之间, 包括 - 3 3 3 3 3 和 3 3 3 之间。

The table below summarizes the kinds of intervals you may need to consider while studying functions and their domains:
::下表概述了您在研究函数及其领域时可能需要考虑的间隔类型:

Interval notation	Inequality notation	Description
$\begin{aligned} [a, b] \end{aligned}$	$\begin{aligned} a \leq x \leq b \end{aligned}$	The value of x is between a and b , including a and b , where a , b are real numbers.
$\begin{aligned} (a, b) \end{aligned}$	$\begin{aligned} a < x < b \end{aligned}$	The value of x is between a and b , not including a and b .
$\begin{aligned} [a, b) \end{aligned}$	$\begin{aligned} a \leq x < b \end{aligned}$	The value of x is between a and b , including a , but not including b .
$\begin{aligned} (a, b] \end{aligned}$	$\begin{aligned} a < x \leq b \end{aligned}$	The value of x is between a and b , including b , but not including a .
$\begin{aligned} (a, \infty) \end{aligned}$	$\begin{aligned} x > a \end{aligned}$	The value of x is strictly greater than a .
$\begin{aligned} [a, \infty) \end{aligned}$	$\begin{aligned} x \geq a \end{aligned}$	The value of x is greater than or equal to a.
$\begin{aligned} (- \infty, a) \end{aligned}$	$\begin{aligned} x < a \end{aligned}$	The value of x is strictly less than a.
$\begin{aligned} (- \infty, a] \end{aligned}$	$\begin{aligned} x \leq a \end{aligned}$	The value of x is less than or equal to a .

Inequalities
::不平等

In another section, we discussed inequalities and briefly noted the interval notation that could be used.
::在另一节中,我们讨论了不平等问题,并简要地指出了可以使用的间隔标记。

A compound inequality is an inequality that combines two other inequalities. For example, $\begin{aligned} x < - 3 or x > 0 \end{aligned}$ . The "or" indicates that the solution is the union of the graphs. Thus, any number that fits at least one inequality would be valid.
::复合不平等是一种将另外两种不平等结合起来的不平等。例如, x< 3 或 x> 0。 “ 或” 表示解决方案是图形的组合。因此, 任何符合至少一种不平等的数字都是有效的。

Another example is $\begin{aligned} x > - 5 a n d x < 2 \end{aligned}$ or, when appropriate, $\begin{aligned} - 5 < x < 2 \end{aligned}$ . The "and" indicates the solution is the intersection of the two graphs. Thus, a number must make both inequalities valid to be valid.
::另一个例子是 x5 和 x < 2 或酌情 - 5 < x < 2 。 “ 并且” 表示解决方案是两个图形的交叉点。因此, 数字必须使两个不平等都有效。

The same options for expressing inequalities in interval notation can be used to describe the of functions, as explored in the later examples.
::如下文的例子所探讨的,在间隔标记中表达不平等的相同选项可用于描述功能。

Examples
::实例

Example 1
::例1

Identify the sets described:
::查明所述各套资料:

a) $\begin{aligned} (- 3, 9] \end{aligned}$
:a) (-3,9)

Solution:
::解决方案 :

The set of numbers between -3 and 9, ‘‘not including’’ the actual value of -3, but ‘‘including’’ 9.
::数字组在 -3和9之间,不包括实际值 -3,但包括_9。

b) $\begin{aligned} [- 23, 12] \end{aligned}$
:b) [-23、12]

Solution:
::解决方案 :

The set of numbers between -23 and 12, ‘‘including’’ the values -23 and 12.
::在 -23 和 12 之间的数组, 包括值 - 23 和 12 。

c) $\begin{aligned} (- \infty, 0) \end{aligned}$
::c) (,0)

Solution:
::解决方案 :

All numbers less than zero, not including zero itself.
::所有数字小于零,不包括零本身。

Example 2
::例2

a) Describe the set shown in the image using interval notation.
::a) 使用间距符号描述图像中显示的数据集。

lesson content

Solution:
::解决方案 :

b) $\begin{aligned} (- \infty, 3), (0, \infty) \end{aligned}$
:b) (,3),(0,)

Since negative infinity cannot be reached, the set is opened with "(". It is then closed with ")" because 3 is not included. The set is reopened with "(" since 0 is not included and closed with ")" since positive infinity cannot be reached, either.
::由于无法达到负无穷度, 设置以“ (” 开始, 然后以“ () ) 关闭, 因为3 不包括。设置以“ (” 重新打开, 因为 0 不包含, 并且以“ () ” 关闭, 因为正无穷度也无法实现。

Example 3
::例3

Sketch the graph of the function $\begin{aligned} f (x) = \frac{1}{2} x - 6 \end{aligned}$ on the interval [-4, 12).
::在间隔[4, 12] 上绘制函数 f(x)=12x- 6的图示 [, 12] 。

Solution:
::解决方案 :

The figure below shows a graph of $\begin{aligned} f (x) = \frac{1}{2} x - 6 \end{aligned}$ on the given interval:
::下图显示给定间隔的 f( x) = 12x- 6 的图形 :

Example 4
::例4

Describe the specified intervals, using interval notation:
::描述指定的间隔, 使用间距标记 :

a) All positive numbers
:a) 所有正数

Solution:
::解决方案 :

$\begin{aligned} (0, \infty) \end{aligned}$

Zero is neither positive nor negative, so the “(“ is used to specify that zero is ‘‘not’’ included. Since there is no maximum positive number, we specify that infinity is the upper value, and use “)” because positive infinity cannot be reached.
::零既不是正数,也不是负数,因此“(“)是用来具体说明零是非。由于没有最大正数,我们具体规定无穷无尽是上值,使用“)”因为无法达到正无穷无尽。

b) The numbers between -8 and 242, including both
:b) -8至242之间的数字,包括两个数字

Solution:
::解决方案 :

$\begin{aligned} [- 8, 242] \end{aligned}$

The “[“ is used on both ends because both values are included.
::“[“用于两个目的,因为两个数值都包括在内。

c) All negative numbers, zero, and the positive numbers up to and including 9
:c) 所有负数(零)和正数(截至9岁,含9岁)

Solution:
::解决方案 :

$\begin{aligned} (- \infty, 9] \end{aligned}$

The “(“ denotes that negative infinity cannot be reached and “]” on the other end specifies that 9 is included in the set.
::““表示不可能达到负无限,”另一端的“]”写明9列入整套。

Example 5
::例5

Return to the problem in the Introduction: To specify that the graph of the cost of lunch includes only values between $3.75 and $15, specify the interval of the domain as [3.75, 15].
::回到导言中的问题:具体说明午餐成本图只包括3.75至15美元之间的价值,将域间距指定为[3.75、15]。

Example 6
::例6

a) Describe the specified intervals, using interval notation:
:a) 说明规定的间隔,使用间距标记:

i) All negative numbers
Solution:
$\begin{aligned} (- \infty, 0) \end{aligned}$
Since there is no maximum negative number, we specify that infinity is the lower value, and use “(” because negative infinity cannot be reached. Zero is neither positive nor negative, so the “)“ is used to specify that zero is ‘‘not’’ included.

ii) The numbers between 5 and 12, including 5, but not 12
Solution:
$\begin{aligned} [5, 12) \end{aligned}$
The “[“ is used to open the set because 5 is included. The ")" is used to close because 12 is not included.

iii) Negative numbers down to -6, zero, and all positive numbers
Solution:
$\begin{aligned} [- 6, \infty) \end{aligned}$
The “[“ is used because -6 is included, but positive infinity cannot be reached, so ")" is used.
:i) 所有负数解答,0)由于没有最大负数,我们具体规定无限值为低值,使用“(......),因为负无限值无法达到。零既不是正数,也不是负数,因此“(......)”用于具体说明零为Not(包括)。 (二)数字介于5至12之间,包括5,但不是12 溶:[5,12] [“用于打开套件,因为包括了5个。“(......)”用于关闭,因为不包括12个。 (三)负数降至-6,零,所有正数解答:[——6,]使用““因为包括6个,但无法达到正无限度,所以”)。

b) Describe the domain for the given images using interval notation:
::b) 使用间距符号描述给定图像的域 :

a)		b)

Solutions:
::解决办法:

The domain of graph a) is the set of $\begin{aligned} x \end{aligned}$ - values starting with the included -6 and ending at 4, which is not included: [-6, 4). The domain of graph b) is the set of $\begin{aligned} x \end{aligned}$ - values starting with the included -6 and ending at 7, which is not included : [-6, 7).
::图a)的域是一组X值,从包括的 -6开始,至4时结束,未包括:[6,4] 图b的域是一组X值,从包括的 -6开始,至7时结束,未包括:[6,7]。

c) Describe the range in the sets in the images above using interval notation.
::c) 使用间距符号描述以上图像中的数据集范围。

Solutions:
::解决办法:

The range of graph a) is the set of $\begin{aligned} y \end{aligned}$ -values from -3 (not included) to 4 (included): (-3, 4]. The range of graph b) is the set of $\begin{aligned} y \end{aligned}$ -values from -1 (included) to 6 (not included): [-1, 6).
::图a的范围是Y值的一组,从-3(未包括在内)到4(包括)3,4)]。图b的范围是Y值的一组,从-1(包括)到6(未包括在内):[1,6]。

Review
::回顾

Write the following in interval notation:
::在间距符号中写入以下文字 :

$\begin{aligned} - 3 \leq x < 1 \end{aligned}$
::- 3x<1

$\begin{aligned} 0 < x < 2 \end{aligned}$
::0 <x <2

$\begin{aligned} x > - 3 \end{aligned}$
::x% 3

$\begin{aligned} x \leq 2 \end{aligned}$
::x% 2

Solve and put your answer in interval notation:
::解答并写上你的答覆的间距符号:

$\begin{aligned} - 2 x + 3 < 1 \end{aligned}$
::-2x+3 < 1

$\begin{aligned} 7 x + 4 \leq 2 x - 6 \end{aligned}$
::7x+42x-6

For each number line, write the given set of numbers in interval notation:
::对于每一数字行,请在间隔编号中填写给定的一组数字:

Name the domain and range for graph, using interval notation:
::使用间距符号命名图形的域和范围 :

Express the following sets using interval notation, then sketch them on a number line:
::使用间距符号表示以下各组,然后用数字线将其绘制成草图:

{ $\begin{aligned} x : - 1 \leq x \leq 3 \end{aligned}$ }
::x: -1x3}

{ $\begin{aligned} x : - 2 \leq x < 1 \end{aligned}$ }
::{x:-2x<1}

A is the set of all numbers bigger than 2 but less than or equal to 5.
::A 是指所有数字的一组,数字大于2但小于或等于5。

{ $\begin{aligned} x : - 3 < x < \infty \end{aligned}$ }
::{x: -3 <x} {x: -3 <x}

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

章节大纲

常规

间距

Introduction ::导言

Real Values and Intervals ::实际价值和间数

Inequalities ::不平等

Examples ::实例

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Real Values and Intervals
::实际价值和间数

Inequalities
::不平等

Examples
::实例

Review
::回顾

Review (Answers)
::回顾(答复)