Course: 2.5 增加和减少 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 增长和减少

Collapse Expand
增长和减少
Introduction
::导言

Analyzing a function is a careful process that begins with classification by family, determining the domain, range, , and extrema . Determining when functions increase and decrease is the next step in this process. Consider this graph of the average temperature per month during 2015 in Las Vegas:
::分析函数是一个谨慎的过程,首先从按家庭分类开始,确定域、范围、和极限。确定函数增减的时间是这一过程的下一个步骤。考虑2015年在拉斯维加斯每月平均温度的图表 :

Moving from left to right along the graph, the average monthly temperatures increase from the beginning of the year until the 8th month. Then the temperature decreases until the end of the year. For those who live in the Northern Hemisphere, this behavior makes sense, since August is usually the hottest month in that region of the Earth. Indeed, we all have a graph like this in our minds when we make decisions relating to seasonal events.
::沿着图表从左向右移动, 平均月温度从年初到第8个月上升。然后温度下降到年底。对于生活在北半球的人来说, 这种行为是有道理的, 因为8月通常是地球这个地区最热的月份。事实上, 当我们做出与季节性事件有关的决定时, 我们脑中都有这样的图表。

Increasing and Decreasing Functions
::增加和减少函数

A function $\begin{aligned} f (x) \end{aligned}$ is increasing on an interval $\begin{aligned} (a, d) \end{aligned}$ if $\begin{aligned} f (b) \leq f (c) \end{aligned}$ for any $\begin{aligned} b and c \end{aligned}$ in the interval where $\begin{aligned} b < c \end{aligned}$ .
::函数f(x)在(a)和(d)间隔内增加,如果(b)f(c)在(b) <c)间隔内的任何 b 和 c 间隔内增加。

An interval is said to be strictly increasing if $\begin{aligned} f (b) < f (c) \end{aligned}$ for any $\begin{aligned} b and c \end{aligned}$ i n the interval where $\begin{aligned} b < c \end{aligned}$ .
::如果(b) <f(c)在(b) <c)的间隔内的任何 b 和 c 之间的间隔为 f(b) <f(c) < f(c) > ,则时间间隔将严格增加。

The formal definition of decreasing and strictly decreasing is identical to the definition of increasing with one of the inequality signs reversed.

::减少和严格减少的正式定义与增加的定义相同,不平等迹象之一被逆转。

A function is monotonic on an interval if it is either nonincreasing or nondecreasing on the interval. A function that is nonincreasing is either decreasing or constant, and a function that is nondecreasing is either increasing or constant.
::一个函数是一个间隔的单体函数,如果该间隔不增加或不减少。一个不增加的函数是递减或常数,一个非裁减的函数是递减或常数。

Graphing devices can be used to determine if a function is increasing or decreasing by visually analyzing the graph. A function is increasing if the graph moves up when we look at the graph from left to right. A function is decreasing if the graph moves down when we look at the graph from left to right. These ideas are further explained in the following video:
::图形设备可以用来通过直观分析图形来确定一个函数是增加还是减少。当我们从左向右查看图形时,如果图形从左向右向上移动,函数正在增加。当我们从左向右查看图形时,图形向下移动,函数正在减少。以下视频将进一步解释这些想法:

Examples
::实例

Example 1
::例1

Identify which of the parent functions are monotonically increasing on their domains.
::确定哪些母函数在其域域上单数增加。

Solution:
::解决方案 :

Of the basic function families, the monotonically increasing functions are:
::在基本功能家庭中,单质增加的职能是:

$\begin{aligned} f (x) = x, g (x) = x^{3}, h (x) = \sqrt{x}, k (x) = e^{x}, m (x) = \ln x, and n (x) = \frac{1}{1 + e^{- x}} . \end{aligned}$
::f(x) =x, g(x) =x3, h(x) =x, k(x) =ex, m(x) =ln_x, n(x) =11+e-x。

The only basic functions that are not monotonically increasing are:
::唯一不单质增加的基本功能是:

$\begin{aligned} f (x) = x^{2}, g (x) = | x |, h (x) = \frac{1}{x}, and k (x) = \sin x . \end{aligned}$
::f(x) =x2,g(x) x,h(x) =1x, k(x) =sinx。

Example 2
::例2

Identify whether the green, red, or blue function is monotonically increasing, and explain why:
::确定绿色、红色或蓝色函数是单质增长,并解释原因:

Solution:
::解决方案 :

The green function is defined on a discrete domain along the line $\begin{aligned} y = x + 2 \end{aligned}$ . While the discrete values clearly increase, the definition requires that any two points can be chosen in an interval. This is impossible, so the green function is not monotonically increasing.
::绿色函数在 y=x+2 行的离散域上定义,虽然离散值明显增加,但该定义要求可以在间隔内选择任何两个点。这是不可能的,因此绿色函数不是单调增加的。

The red function is nondecreasing on the interval $\begin{aligned} (- 1, 3) \end{aligned}$ , so it is monotonic.
::红函数在间隔( - 1,3) 上没有降序, 所以是单声道。

The blue function seems to be $\begin{aligned} y = \sqrt{x} - 2 \end{aligned}$ is increasing everywhere for the region displayed on the graph. This function is monotonic for $\begin{aligned} x \in [0, \infty) \end{aligned}$ .
::蓝色函数似乎为 y=x-2, 在图中显示的区域中, 各地的 y=x-2 都在增加。这个函数是 x {% {0} 的单体函数。

Example 3
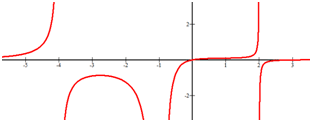
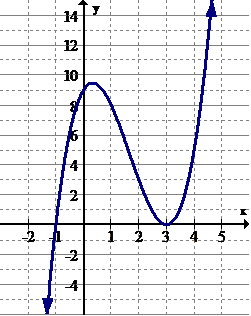
::例3

Estimate the intervals where the function is increasing and decreasing:
::估计该职能增减的间隔:

Solution:
::解决方案 :

Increasing: $\begin{aligned} x \in (- \infty, - 4) \cup (- 2, 1.5) \end{aligned}$
::增加: x(),- 4) (− 2,1.5)

Decreasing: $\begin{aligned} x \in (- 4, - 2) \cup (1.5, \infty) \end{aligned}$
::衰减: x( - 4, - 2) ( 1. 5, )

Note that open intervals are used because at $\begin{aligned} x = - 4, - 2, 1.5 \end{aligned}$ , the function is neither increasing nor decreasing. This is the point where the function changes its monotonicity from increasing to decreasing.
::请注意, 使用开放间隔是因为 x4, −2, 2.5 函数既不增不减。这是函数将其单音从增到减的点。

Example 4
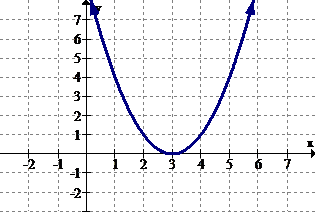
::例4

Estimate the intervals where the following function is increasing and decreasing:
::估计下列职能增减的间隔:

Solution:
::解决方案 :

Increasing: $\begin{aligned} x \in (- \infty, - 1.5) \cup (1.5, \infty) \end{aligned}$ . Decreasing: $\begin{aligned} x \in (- 1.5, 1.5) \end{aligned}$
::递增: x(,-1.5)(1.5,)。递减: x(-1.5,1.5)

Example 5
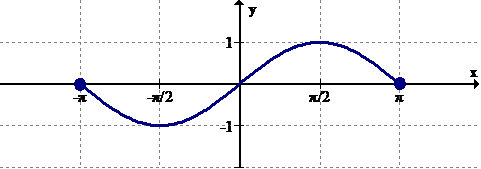
::例5

Estimate where the following function is increasing and decreasing:
::估计下列职能在哪些方面在增加和减少:

Solution:
::解决方案 :

Increasing: $\begin{aligned} x \in (- \infty, - 4) \cup (- 4, - 2.7) \cup (- 1, 2) \cup (2, \infty) \end{aligned}$ . Decreasing: $\begin{aligned} x \in (- 2.7, - 1) \end{aligned}$
::递增: x ( - 4) ( - 4) - 2. 7) ( - 1, 2) ( 2, ) ( 2, ) 。衰减: x( - 2- 7) - 1

Example 6
::例6

A function defined for all real numbers has a global maximum at the point (3, 2), a global minimum at the point (5, -12), and has no relative extrema. What are the intervals where the function is increasing and decreasing?
::为所有实际数字定义的函数在点(3, 2)上具有全球最大值,在点(5, 12)上具有全球最低值,没有相对的外形。函数在增减的间隔是多少?

Solution:
::解决方案 :

Increasing: $\begin{aligned} x \in (- \infty, 3) \cup (5, \infty) \end{aligned}$ . Decreasing: $\begin{aligned} x \in (3, 5) \end{aligned}$
::递增: x(, , , ) (5, ) 。递减: x( 3, 5)

Notice that the intervals define the portion of the domain where this behavior occurs.
::请注意, 间隔会定义该行为发生的域段。

Summary
::摘要

A function $\begin{aligned} f (x) \end{aligned}$ is increasing if $\begin{aligned} f (b) \leq f (c) \end{aligned}$ for any $\begin{aligned} b and c \end{aligned}$ in the interval where $\begin{aligned} b < c \end{aligned}$ .
::函数 f(x) 正在增加, 如果 f(b)\f(c) 在 b < c 的间隔内, 任何 b 和 c 的函数 f(x) 正在增加。

::函数 f(x) 正在增加, 如果 f(b)\f(c) 在 b < c 的间隔内, 任何 b 和 c 的函数 f(x) 正在增加。

A function $\begin{aligned} f (x) \end{aligned}$ is de creasing if $\begin{aligned} f (b) \geq f (c) \end{aligned}$ for any $\begin{aligned} b and c \end{aligned}$ in the interval where $\begin{aligned} b < c \end{aligned}$ .
::函数 f(x) 正在递减, 如果 f(b)\f(c) 在 b < c 的间隔内, 任何 b 和 c 的 f(b)\f)\f(c) 在 b < c 的间隔内。

::函数 f(x) 正在递减, 如果 f(b)\f(c) 在 b < c 的间隔内, 任何 b 和 c 的 f(b)\f)\f(c) 在 b < c 的间隔内。

A function is strictly increasing or strictly decreasing when the function inequalities are strictly less than.
::当功能不平等严重低于功能不平等时,功能正在严格增加或减少。

::当功能不平等严重低于功能不平等时,功能正在严格增加或减少。

A function is monotonic on an interval if it is either nonincreasing or nondecreasing on the interval.
::如果一个函数在间隔上不增不减,则该函数是一个间隔的单体函数。

::如果一个函数在间隔上不增不减,则该函数是一个间隔的单体函数。

Review
::回顾

Use the graph below for 1-2:
::1-2使用下图:

1. Identify the intervals (if any) where the function is increasing.
::1. 确定职能增加的间隔(如果有的话)。

2. Identify the intervals (if any) where the function is decreasing.
::2. 确定职能减少的间隔(如果有的话)。

Use the graph below for 3-4:
::3-4使用下图:

3. Identify the intervals (if any) where the function is increasing.
::3. 确定职能增加的间隔(如果有的话)。

4. Identify the intervals (if any) where the function is decreasing.
::4. 确定职能减少的间隔(如果有的话)。

Use the graph below for 5-6:
::5-6 使用下图 :

5. Identify the intervals (if any) where the function is increasing.
::5. 确定职能增加的间隔(如果有的话)。

6. Identify the intervals (if any) where the function is decreasing.
::6. 确定职能减少的间隔(如果有的话)。

Use the graph below for 7-8:
::7-8 使用下图 :

7. Identify the intervals (if any) where the function is increasing.
::7. 确定职能增加的间隔(如果有的话)。

8. Identify the intervals (if any) where the function is decreasing.
::8. 确定职能减少的间隔(如果有的话)。

Use the graph below for 9-10:
::9-10使用下图:

9. Identify the intervals (if any) where the function is increasing.
::9. 确定职能增加的间隔(如果有的话)。

10. Identify the intervals (if any) where the function is decreasing.
::10. 确定职能减少的间隔(如果有的话)。

11. Give an example of a monotonically increasing function.
::11. 举一个单一增长功能的例子。

12. Give an example of a monotonically decreasing function.
::12. 举一例说明单质递减功能。

13. A function defined for all real numbers has a global maximum at the point (1, 4) and a global minimum at (3, -6), and has no relative extrema or other places with a slope of 0. What are the increasing and decreasing intervals for this function?
::13. 为所有实际数字定义的函数在点(1、4)上具有全球最高值,在全球最低值(3、6)上具有全球最低值(3、6),没有相对的外形或其他斜度为0的位址。

14. A function defined for all real numbers has a global maximum at the point (1, 1) and has no other extrema or places with a slope of 0. What are the increasing and decreasing intervals for this function?
::14. 为所有实际数字定义的函数在点(1、1)上具有全球最高值,没有其它偏差或斜度为0的地方。这一函数的增减间隔是多少?

15. A function defined for all real numbers has a global minimum at the point (5, -15) and has no other extrema or places with a slope of 0. What are the increasing and decreasing intervals for this function?
::15. 为所有实际数字界定的函数在点(5,-15)上具有全球最低值,没有其它偏差或斜度为0的地方。这一函数的增减间隔是多少?

For questions 16-18, use the following information: Sam makes $7.50 per hour at work, and he works anywhere from 15 to 40 hours per week. Occasionally, the store gets very busy, and Sam's boss allows him to work up to 15 hours of overtime. Sam loves the busy weeks because he makes "time-and-a-half," or $11.25, for overtime hours.
::对于问题16-18,请使用以下信息:Sam每小时工作7.50美元,每周工作15至40小时。偶尔,商店非常忙,Sam的老板允许他加班多达15小时。 Sam喜欢繁忙的周,因为他做了“半时半时”或11.25小时加班。

16. Sketch a graph showing Sam's regular income range. Where are the local extrema?
::16. 绘制一张显示萨姆正常收入范围的图,当地极端收入在哪里?

17. What happens to the local extrema if Sam is working a week with overtime? Where are they now?
::17. 如果Sam每周加班工作一周,当地医务室怎么办?他们现在在哪里?

18. Sketch another graph including Sam's regular and overtime income, identifying all local extrema.
::18. 绘制另一幅图,包括萨姆的经常收入和加班收入,标明所有当地极端情况。

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

General

增长和减少

Introduction ::导言

Increasing and Decreasing Functions ::增加和减少函数

Examples ::实例

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Increasing and Decreasing Functions
::增加和减少函数

Examples
::实例

Review
::回顾

Review (Answers)
::回顾(答复)