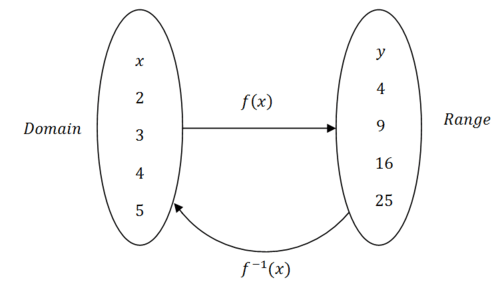
课程： 2.13 函数的反函数

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节函数的逆函数

折叠展开
函数的逆函数
Introduction
::导言

Assume the kidneys can filter out 20% of a drug in the blood every 4 hours. A patient is given one 1,000-milligram dose of a drug. The following function was derived to calculate the amount of the drug in the blood system $\begin{aligned} t \end{aligned}$ days after taking the drug:
::假定肾脏每4小时可以将20%的药物从血液中过滤出来,给病人注射1 000毫米剂量的药物。

$\begin{aligned} A (t) = 1, 000 ({0.26}^{t}) \end{aligned}$

::A(t)=1,000(0.26t)

A blood test is able to detect the presence of the drug if there is at least 0.01 mg in the blood. How many days will it take before the test will come back negative?
::如果血液中至少有0.01毫克的剂量,血液测试能够检测出该药物的存在。在检测结果为阴性之前需要多少天时间?

This question requires that we create a new function, an inverse function, whose domain is amount of the drug in the blood system , and whose range is the amount of time since the drug was ingested. For this problem, the inverse function is $\begin{aligned} t, \end{aligned}$ where A is the amount of the drug in t he system:
::这个问题要求我们创建一个新的函数,一个反函数,其领域是血液系统中的药物数量,其范围是药物摄入以来的时间范围。对于这个问题,反函数是 t,其中A是药物在系统中的数量:

$\begin{aligned} t = \frac{\ln A - \ln 1, 000}{\ln 0.26} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不!

While the fact that exponential and are inverses will be explored more in that chapter, we will introduce and discuss the inverse function in general in this section.
::虽然在该章中将更多地探讨指数化和反向作用这一事实,但我们将在本节中介绍和讨论一般的反向作用。

Algebraic Conditions for the Inverse
::反向的代数条件

Prior to determining if a function has an inverse, we must 1st determine if the function is one-to-one. A one-to-one function is a function in which every element in the range corresponds to exactly one element in the domain. In other words, there is a one-to-one pairing between the elements in the range and domain.
::在确定一个函数是否有反向函数之前,我们必须首先确定该函数是一对一。一对一函数是一个函数,其中范围中每个元素都与域中一个元素完全对应。换句话说,在范围中和域中各元素之间存在一对一对一的对立。

One method to determine if a function is one-to-one is the horizontal line test. The horizontal line test states that a function is one-to-one if any horizontal line drawn through the graph of the function intersects the graph at only one point:
::确定函数是否一对一的一种方法是水平线测试。水平线测试表明,如果通过函数图绘制的任何水平线仅在一个点将图形交叉,则函数为一对一:

A function has an inverse only if it is a one-to-one function.
::函数只有在一对一函数时才具有反向函数。

Inverse Notation
::反反注释

A function is written as $\begin{aligned} f (x) \end{aligned}$ and its inverse is written as $\begin{aligned} f^{- 1} (x) \end{aligned}$ . A common misconception is to see the -1 and interpret it as an exponent and write $\begin{aligned} \frac{1}{f (x)} \end{aligned}$ , but this is not correct. Instead, $\begin{aligned} f^{- 1} (x) \end{aligned}$ should be viewed as a new function whose domain is the range of $\begin{aligned} f (x) \end{aligned}$ and whose range is the domain of $\begin{aligned} f (x) \end{aligned}$ .
::函数 f( x) 写入 f( x) , 其反写为 f- 1( x) 。一个常见的误解是将 -1 解读为 expronent and write 1f( x) , 但这是不正确的。相反, f- 1( x) 应被视为一个新的函数, 其域范围为 f( x) , 范围为 f( x) 域。

In order for two functions to truly be inverses of each other, the following must hold algebraically:
::为使两个功能真正相互对立,必须采用下列代数:

$\begin{aligned} f (f^{- 1} (x)) = x \end{aligned}$ and $\begin{aligned} f^{- 1} (f (x)) = x \end{aligned}$
::f( f- 1 (x)) =x 和 f- 1 (f(x)) =x

The resulting $\begin{aligned} x \end{aligned}$ is in the domain of $\begin{aligned} f \end{aligned}$ for the 1st equation and in the range of $\begin{aligned} f \end{aligned}$ for the 2nd equation.
::所产生的 x 在 f 的域中, 属于第 1 等式 , 而在 f 的域中 , 属于第 2 等式的 f 范围。

Sometimes the inverse of a function can be found algebraically:
::有时函数的反面可以找到代数 :

In the original function, let $\begin{aligned} y = f (x) \end{aligned}$ .
::在原始函数中,让我们 Y=f(x) 。

Then, switch the variables $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::然后,切换变量 x 和 y。

Next, solve for $\begin{aligned} y \end{aligned}$ in terms of $\begin{aligned} x \end{aligned}$ .
::下一步,用 x 解决y 。

Set $\begin{aligned} y = f^{- 1} (x) \end{aligned}$ . This is the inverse function.
::设置 Y=f- 1 (x) 。这是反函数。

Always verify that $\begin{aligned} f (f^{- 1} (x)) = x \end{aligned}$ and $\begin{aligned} f^{- 1} (f (x)) = x \end{aligned}$ .
::总是验证 f( f- 1 (x)) =x 和 f- 1 (f (x) =x 。

Graphically, inverses are reflections in the line $\begin{aligned} y = x \end{aligned}$ . Observe the graphs of $\begin{aligned} y = e^{x} \end{aligned}$ and $\begin{aligned} y = \ln x \end{aligned}$ . Notice how the $\begin{aligned} (x, y) \end{aligned}$ coordinates in one graph become $\begin{aligned} (y, x) \end{aligned}$ coordinates in the other graph:
::图形中,反向是 y=x 线中的反射。观察 y=ex 和 y= ln= x 的图形。注意一个图形中的(x,y) 坐标是如何在另一个图形中变成 (y,x) 坐标的 :

In order to decide whether an inverse is also actually a function, you can use the vertical line test on the inverse function. You can also use the horizontal line test on the original function.
::为了确定反向是否也是函数,您可以在反向函数上使用垂直线测试。也可以在原始函数上使用水平线测试。

Learn, Play, and Explore with Inverse Functions:
::用反向函数学习、玩耍和探索 :

Examples
::实例

Example 1
::例1

Determine the inverse for the function $\begin{aligned} f (x) = y = (x + 1)^{2} + 4 \end{aligned}$ , where $\begin{aligned} x \geq - 1, \end{aligned}$ and then verify the inverse algebraically.
::确定函数 f( x) =y= (x+1) 2+4 的反方值, 此处 x\\\ 1, 然后校验反向代数。

Solution:
::解决方案 :

To find the inverse, switch $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ then solve for $\begin{aligned} y \end{aligned}$ :
::查找反向, 切换 x 和 y , 然后为 y 解答 :

$\begin{aligned} x & = (y + 1)^{2} + 4 \\ x - 4 & = (y + 1)^{2} \\ \sqrt{x - 4} & = y + 1 \\ - 1 + \sqrt{x - 4} & = y = f^{- 1} (x) \end{aligned}$

::x= (y+1) 2+4x-4= (y+1) 2x-4= (y+1) 2x-4=y+1 -1+x-4=y=f-1(x)

To verify algebraically, you must show $\begin{aligned} x = f (f^{- 1} (x)) = f^{- 1} (f (x)) \end{aligned}$ :
::要校验代数, 您必须显示 x=f( f- 1 (x)) = f- 1 (f(x) :

$\begin{aligned} f (f^{- 1} (x)) & = f (- 1 + \sqrt{x - 4}) \\ = ((- 1 + \sqrt{x - 4}) + 1)^{2} + 4 \\ = {(+ \sqrt{x - 4})}^{2} + 4 \\ = x - 4 + 4 = x \end{aligned}$

::f( f- 1( x)) = f( 1+x-4) = ( 1+x-4) = ( 1+x-4) +1) 2+4 = (+x-4) 2+4= (+x-4) 2+4= x-4+4+4=x

$\begin{aligned} f^{- 1} (f (x)) & = f^{- 1} ((x + 1)^{2} + 4) \\ = - 1 + \sqrt{((x + 1)^{2} + 4) - 4} \\ = - 1 + \sqrt{(x + 1)^{2}} \\ = - 1 + x + 1 = x \end{aligned}$

::f- 1 (f(x)) = f- 1 ((x+1) 2+4) @% 1+ ((x+1) 2+4)- 4=1+(x+1) 1+(x+1) 1+(x+1) 2+1=x

Note the original function had its domain restricted so it would pass the horizontal line test. Otherwise , the inverse relation would not have passed a vertical line test and would not have been a function.
::注意原始函数有其域限制, 以便通过水平线测试。否则, 反向关系就不会通过垂直线测试, 也不会是一个函数。

Example 2
::例2

Find the inverse of the function and then verify that $\begin{aligned} x = f (f^{- 1} (x)) = f^{- 1} (f (x)) \end{aligned}$ .
::查找函数的反向,然后核实 x=f(f-1(x)) = f- 1(f(x) 。

$\begin{aligned} f (x) = y = \frac{x + 1}{x - 1} \end{aligned}$
:xx) =y=x+1x-1

Solution:
::解决方案 :

Sometimes it is quite challenging to switch $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ and then solve for $\begin{aligned} y \end{aligned}$ . You must be careful with your algebra.
::有时转换 x 和 y 然后为 y 解决问题相当困难。您必须小心代数。

$\begin{aligned} x & = \frac{y + 1}{y - 1} \\ x (y - 1) & = y + 1 \\ x y - x & = y + 1 \\ x y - y & = x + 1 \\ y (x - 1) & = x + 1 \\ y & = \frac{x + 1}{x - 1} \end{aligned}$

::x=y+1y-1x(y- 1)=y+1xy-x=y+1xy-y=x1y(x-1)=x1y=x1y=x1x-x-1)

This function turns out to be its own inverse. Since they are identical, you only need to show that $\begin{aligned} x = f (f^{- 1} (x)) \end{aligned}$ .
::3⁄4 ̄ ̧漯B

$\begin{aligned} f (\frac{x + 1}{x - 1}) = \frac{(\frac{x + 1}{x - 1}) + 1}{(\frac{x + 1}{x - 1}) - 1} = \frac{x + 1 + x - 1}{x + 1 - (x - 1)} = \frac{2 x}{2} = x \end{aligned}$
::f( x+1x-1) = (x+1x-1) = (x+1x-1) +1(x+1x-1) +1(x+1x-1) = 1x 1+1x-1x+1(x-1) =2x2=x

Example 3
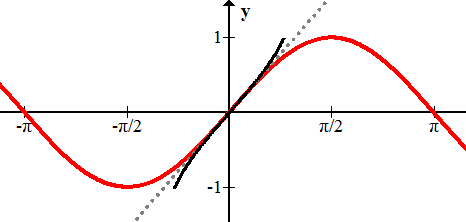
::例3

What is the inverse of $\begin{aligned} f (x) = y = \sin x \end{aligned}$ ?
::F(x)=y=sinx的反义值是什么?

Solution:
::解决方案 :

The sine function does not pass the horizontal line test, so its inverse is not a function:
::正弦函数不会通过水平线测试, 因此它的反向不是一个函数 :

However, if you restrict the domain to just the part of the $\begin{aligned} x \end{aligned}$ -axis between $\begin{aligned} - \frac{π}{2} \end{aligned}$ and $\begin{aligned} \frac{π}{2} \end{aligned}$ , then it will pass the horizontal line test and the inverse will be a function:
::但是,如果您将域限制在% 2 和% 2 之间的 X 轴部分, 它会通过水平线测试, 而反向将是一个函数 :

The inverse of the sine function is called the arcsine function, $\begin{aligned} f (x) = \sin^{- 1} (x) \end{aligned}$ , and is shown in black. It is truncated so that it only inverts a part of the whole sine wave. You will study periodic functions and their inverses in more detail later.
::正弦函数的反义称为arcsine 函数, f(x) =sin- 1(x) , 以黑色显示。它被缩短, 因而它只能反转整个正弦波的一部分。您以后将更详细地研究周期函数及其反函数。

Example 4
::例4

Determine the inverse of $\begin{aligned} f (x) = 5 + \frac{x}{2} \end{aligned}$ . Verify that the inverse is actually the inverse.
::确定 f( x) = 5+x2 的逆数。验证反数实际上是反数。

Solution:
::解决方案 :

To find the inverse,
::为了找到反面的答案

$\begin{aligned} y & = 5 + \frac{x}{2} \\ x & = 5 + \frac{y}{2} \\ x - 5 & = \frac{y}{2} \\ 2 (x - 5) & = y = f^{- 1} (x) \end{aligned}$

::y= 5+x2x=5+y2x- 5=y22(x- 5)=y=f- 1(x)

Verification:
::核查:

$\begin{aligned} 2 (5 + \frac{x}{2} - 5) = 2 (\frac{x}{2}) = x \end{aligned}$
::2(5+x2 - 5)=2(x2)=x

$\begin{aligned} 5 + \frac{2 (x - 5)}{2} = 5 + x - 5 = x \end{aligned}$
::5+2(x-5-2)2=5+x-5=x

They are truly inverses of each other.
::他们确是互相背离的。

Example 5
::例5

Determine if $\begin{aligned} f (x) = \frac{3}{7} x - 21 \end{aligned}$ and $\begin{aligned} g (x) = \frac{7}{3} x + 21 \end{aligned}$ are inverses of one another.
::确定 f( x) = 37x- 21 和 g( x) = 73x+21 是否是彼此的反义。

Solution:
::解决方案 :

Even though $\begin{aligned} f (x) = \frac{3}{7} x - 21 \end{aligned}$ and $\begin{aligned} g (x) = \frac{7}{3} x + 21 \end{aligned}$ have some inverted pieces, they are not inverses of each other. In order to show this, you must show that the composition does not simplify to $\begin{aligned} x \end{aligned}$ : $\begin{aligned} \frac{3}{7} (\frac{7}{3} x + 21) - 21 = x + 9 - 21 = x - 12 \neq x \end{aligned}$
::尽管 f( x) = 37x- 21 和 g( x) = 73x+21 有一些反转的碎片, 但两者并非反转的反相。要显示这一点, 您必须显示其组成不简化为 x: 37( 73x+21) - 21=x+9- 21=x- 12x

Example 6
::例6

Determine the inverse of $\begin{aligned} f (x) = \frac{x}{x + 4} \end{aligned}$ .
::确定 f(x) =xx+4 的逆值。

Solution:
::解决方案 :

To find the inverse, switch x and y:
::要找到反向, 切换 x 和 y :

$\begin{aligned} f (x) & = y = \frac{x}{x + 4} \\ x & = \frac{y}{y + 4} \\ x (y + 4) & = y \\ x y + 4 x & = y \\ x y - y & = - 4 x \\ y (x - 1) & = - 4 x \\ f^{- 1} (x) & = y = - \frac{4 x}{x - 1} \end{aligned}$

::f(x) =y=xx+4x=yy+4x(y+4) =yxy+4x=yxy=y*4xy(x) -y*4xy(x) -y*4xy(x) -1) *4xf -1(x)=y*4xxx-1

Summary
::摘要

A function is one-to-one if every element in the range corresponds to exactly one element in the domain.
::函数为一对一,如果范围中的每一元素与域内一个元素完全对应。

The horizontal line test states that a function is one-to-one if any horizontal line drawn through the graph of the function intersects the graph at only one point .
::水平线测试显示,如果通过函数图形绘制的任何水平线仅在一个点交叉图形,则函数为一对一。

A function has an inverse only if it is a one-to-one function.
::函数只有在一对一函数时才具有反向函数。

Two functions are inverses if $\begin{aligned} x = f (f^{- 1} (x)) = f^{- 1} (f (x)) \end{aligned}$ .
::如果 x=f( f- 1 (x)) =f- 1(f(x)) 则两个函数为反函数。

To algebraically solve for the inverse function, switch the variables $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ in the function and then solve for $\begin{aligned} y \end{aligned}$ in terms of $\begin{aligned} x \end{aligned}$ .
::对反函数的代数解析,将函数中的变量 x 和 y 切换,然后以 x 为y 解析。

Review
::回顾

Use the function $\begin{aligned} f (x) = x^{3} \end{aligned}$ for the following problems:
::使用函数 f( x) =x3 处理下列问题 :

1. Sketch $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} f^{- 1} (x) \end{aligned}$ .
::1. Spetch f(x) 和 f- 1(x) 。

2. Find $\begin{aligned} f^{- 1} (x) \end{aligned}$ algebraically. It is actually a function?
::2. 查找 f-1(x) 代数。它实际上是一个函数吗 ?

3. Verify algebraically that $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} f^{- 1} (x) \end{aligned}$ are inverses.
::3. 从代数上核实f(x)和f-1(x)是反向的。

Use the function $\begin{aligned} g (x) = \sqrt{x}, x \geq 0 \end{aligned}$ , for the following problems:
::使用函数 g( x) =x, x/0, 处理下列问题 :

4. Sketch $\begin{aligned} g (x) \end{aligned}$ and $\begin{aligned} g^{- 1} (x) \end{aligned}$ .
::4. Spetch g(x) 和 g- 1(x) 。

5. Find $\begin{aligned} g^{- 1} (x) \end{aligned}$ algebraically. It is actually a function?
::5. 查找 g-1(x) 代数。它实际上是一个函数吗 ?

6. Verify algebraically that $\begin{aligned} g (x) \end{aligned}$ and $\begin{aligned} g^{- 1} (x) \end{aligned}$ are inverses.
::6. 核实g(x)和g-1(x)是反向的代数。

Use the function $\begin{aligned} h (x) = | x | \end{aligned}$ f or the following problems:
::使用此函数 h( x)\\\\\\\\\\\\\\\可以回答下列问题 :

7. Sketch $\begin{aligned} h (x) \end{aligned}$ and $\begin{aligned} h^{- 1} (x) \end{aligned}$ .
::7. Spetch h(x) 和 h-1(x) 。

8. Find $\begin{aligned} h^{- 1} (x) \end{aligned}$ algebraically. It is actually a function?
::8. 查找 h-1(x) 代数。它实际上是一个函数吗 ?

9. Verify graphically that $\begin{aligned} h (x) \end{aligned}$ and $\begin{aligned} h^{- 1} (x) \end{aligned}$ are inverses.
::9. 以图形方式验证 h(x) 和 h- 1(x) 是反向的。

Use the function $\begin{aligned} j (x) = 2 x - 5 \end{aligned}$ f or the following problems:
::使用函数 j( x) = 2x- 5 处理下列问题 :

10. Sketch $\begin{aligned} j (x) \end{aligned}$ and $\begin{aligned} j^{- 1} (x) \end{aligned}$ .
::10. Spletch j(x) 和 j-1(x) 。

11. Find $\begin{aligned} j^{- 1} (x) \end{aligned}$ algebraically. It is actually a function?
::11. 查找 j-1(x) 代数。它实际上是一个函数吗 ?

12. Verify algebraically that $\begin{aligned} j (x) \end{aligned}$ and $\begin{aligned} j^{- 1} (x) \end{aligned}$ are inverses.
::12. 从代数上核实j(x)和j-1(x)是反向的。

13. Use the horizontal line test to determine whether or not the inverse of $\begin{aligned} f (x) = x^{3} - 2 x^{2} + 1 \end{aligned}$ is also a function.
::13. 使用水平线测试来确定 f( x) =x3 - 2x2+1 的反向是否也是一种函数。

14. Are $\begin{aligned} g (x) = \ln (x + 1) \end{aligned}$ and $\begin{aligned} h (x) = e^{x - 1} \end{aligned}$ inverses? Explain.
::14. g(x) = ln(x+1) 和 h(x) = ex- 1 反义吗? 解释。

15. If you were given a table of values for a function, how could you create a table of values for the inverse of the function?
::15. 如果给您一个函数的数值表,您如何为函数的反向创建数值表?

16. In many countries, the temperature is measured in degrees Celsius. In the U.S., we typically use degrees Fahrenheit. For travelers, it is helpful to be able to convert from one unit of measure to another.
::16. 在许多国家,温度是以摄氏度测量的,在美国,我们通常使用华氏度,对于旅行者来说,能够从一个计量单位转换为另一个计量单位是有益的。

The temperature at which water freezes will give us one point on a line in which $\begin{aligned} x \end{aligned}$ represents the degrees in Celsius and $\begin{aligned} y \end{aligned}$ represents the degrees in Fahrenheit. Water freezes at 0°C and 32 ° F, so the 1st point is (0, 32). The temperature at which water boils gives us the 2nd point (100, 212), because water boils at 100 ° C or 212 ° F. Use this information to show that the equation to convert from Celsius to Fahrenheit is $\begin{aligned} y = \frac{9}{5} x + 32 \end{aligned}$ or $\begin{aligned} F = \frac{9}{5} C + 32 \end{aligned}$ .
::水冻结的温度将给我们以摄氏度和y代表华氏度的线上一个点。水冻结在0°C和32°F, 因此第一个点是( 0, 32) 。水沸腾的温度给我们带来第二个点( 100, 212) , 因为水沸腾在100°C或212. F。使用此信息显示, 将摄氏度转换为法氏度的方程是y=95x+32 或 F=95C+32 。

Find the inverse of the equation above by solving for $\begin{aligned} C, \end{aligned}$ to derive a formula that will allow us to convert from Fahrenheit to Celsius.
::找到上面方程式的反面, 解决C, 得出一个公式, 使我们能够从法赫里内海特转换成摄氏。

Show that your inverse is correct by showing that the composition of the two functions simplifies to either $\begin{aligned} F \end{aligned}$ or $\begin{aligned} C \end{aligned}$ (depending on which one you put into the other).
::显示两个函数的构成简化为 F 或 C (取决于您将哪个函数简化为另一个函数) , 以此显示您的反向是正确的。

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

2.13 函数的反函数

章节大纲

常规

函数的逆函数

Introduction
::导言

Algebraic Conditions for the Inverse
::反向的代数条件

Inverse Notation
::反反注释

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)

章节大纲

常规

函数的逆函数

Introduction ::导言

Algebraic Conditions for the Inverse ::反向的代数条件

Inverse Notation ::反反注释

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Algebraic Conditions for the Inverse
::反向的代数条件

Inverse Notation
::反反注释

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)