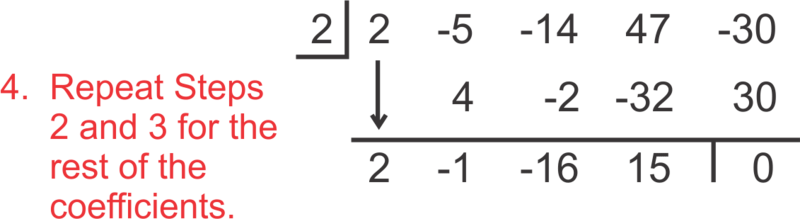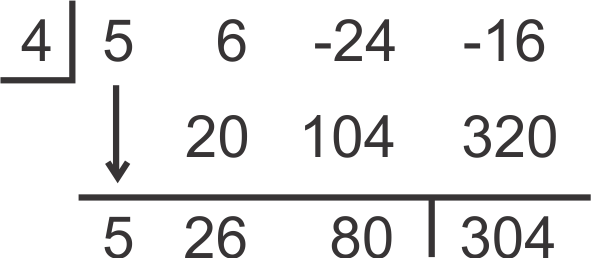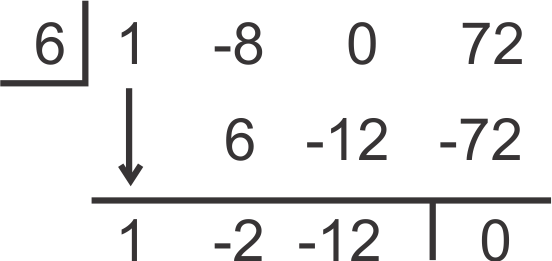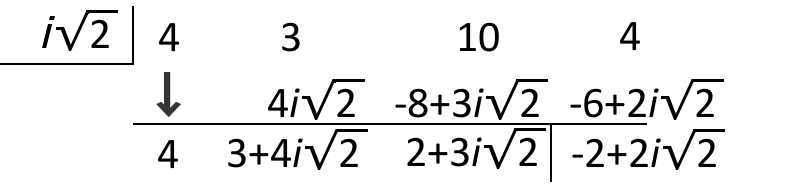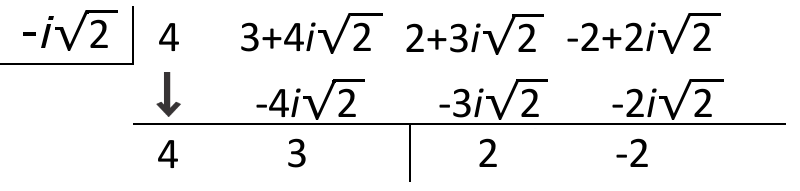课程： 3.4 多元体合成部

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节多多边合成科合成科

折叠展开
多多边合成科合成科
Introduction
::导言

Consider the task of needing to find the zeros of the function $\begin{align*}f(x)={x}^{4}+{x}^{3}-25{x}^{2}-37x+60. \end{align*}$ Factoring seems to be a daunting task. In fact, computer algebra systems are now free and available to factor this polynomial easily.
::考虑需要找到函数 f( x) =x4+x3 - 25x2 - 37x+60 的零。保理似乎是一项艰巨的任务。事实上, 计算机代数系统现在可以自由使用, 很容易将这一多数值因素考虑在内。

While we have the option of using software to do the work, however, several classic techniques remain useful. One technique is synthetic division of polynomials, which is based on the process of long division .
::虽然我们可以选择使用软件来完成这项工作,但一些经典技术仍然有用。一种技术是合成的多语种分类,其基础是长期分割的过程。

Polynomial Long Division
::单体长分区

We use to determine the factors of a polynomial in a similar way that we use long division to divide integers .
::我们用来确定多面性因素, 类似我们用长分割法来分隔整数。

W henever you want to divide a polynomial by a polynomial, you can use a process called polynomial long division . This process is similar to long division for integers . If we would like to divide
::每当您想要用多数值将多数值除以时,您可以使用一个叫做多数值长分割的过程。这个过程类似于整数的长分隔。如果我们想要分隔

$\begin{aligned} \frac{x^{2} + 3 x + 2}{x + 1}, \end{aligned}$
$\begin{align*}\frac{x^2+3x+2}{x+1},\end{align*}$
::x2+3x+2x+1,

we can transfer the fraction form to the long division format:
::我们可以将分数格式转换为长分割格式 :

.

Step 1: Divide the 1st term in the numerator ( $\begin{align*}x^2\end{align*}$ ) by the 1st term in the denominator ( $\begin{align*}x\end{align*}$ ). Write this result above the division bar in your answer. In this case, $\begin{align*}\frac{x^2}{x} = x\end{align*}$ :
::第1步:将分子(x2)中的第一个术语除以分母(x)中的第一个术语。将此结果写在您回答的分隔栏上方。在此情况下, x2x=x:

.

Step 2: Multiply the denominator ( $\begin{align*}x+1\end{align*}$ ) by the result from Step 1 ( $\begin{align*}x\end{align*}$ ), and put the new result below your numerator. Then, subtract to get your new polynomial. This is similar to the process of regular number long division!
::步骤2:将分母(x+1)乘以第1步(x)的结果,然后将新结果置于分子下方。然后,减去以获得新的多数值。这与普通数字长分隔法相似!

Step 3: Divide the 1st term in the new polynomial ( $\begin{align*}2x\end{align*}$ ) by the 1st term in the denominator ( $\begin{align*}x\end{align*}$ ). Put this result above the division bar in your answer. Multiply, subtract, and repeat this process until you cannot repeat it anymore:
::步骤 3 : 将新多面体(2x) 中的第一个术语除以分母 (x) 中的第一个术语。在您的答复中将此结果置于除法栏以上。乘以、减去并重复此进程, 直到您不能再重复它 :

.

Since there is no remainder, $\begin{align*}\frac{x^2+3x+2}{x+1}=x+2.\end{align*}$
::由于没有剩余部分, x2+3x+2x+1=x+2。

Here is another example of using long division to divide:
::以下是另一个用长分割来分割的例子:

$\begin{aligned} \frac{x^{2} + 6 x - 7}{x - 1} \end{aligned}$
$\begin{align*}\frac{x^2+6x-7}{x-1}\end{align*}$
::x2+6x-7x-1

Step 1: Divide the 1st term in the numerator by the 1st term in the denominator, and put this in your answer. Therefore , $\begin{align*}\frac{x^2}{x} = x\end{align*}$ .
::第1步:将分子中的第一个词除以分母中的第一个词,然后将其放入您的答复中。因此, x2x=x。

$\begin{aligned} (x - 1) \overset{x}{| \bar{x^{2} + 6 x - 7}} \end{aligned}$
$\begin{align*}(x-1) \overset{{\color{red}x}}{|\overline{x^2+6x-7}}\end{align*}$
:x- 1) @x2+6x- 7x

Step 2: Multiply the denominator by this number (variable) and put it below your numerator, subtract and get your new polynomial:
::第2步:将分母乘以此数(可变)并将其置于分子下方,减去并获得新的多数值 :

$\begin{aligned} (x - 1) \overset{x}{| \bar{x^{2} + 6 x - 7}} \\ \underline{x^{2} - x} \\ 7 x . \end{aligned}$
$\begin{align*}&(x-1)\overset{{\color{red}x} \qquad \quad}{|\overline{x^2+6x-7}}\\ &\qquad \ \ \underline{\; x^2-x \;}\\ & \qquad \qquad \ 7x.\end{align*}$
:x1)x2+6x7xxxxxx_x_7x)

Step 3: Repeat the process until you cannot repeat it anymore:
::第3步:在不能再重复之前,重复此进程 :

$\begin{aligned} (x - 1) \overset{x + 7}{| \bar{x^{2} + 6 x - 7}} \\ \underline{x^{2} - x ↓} \\ 7 x - 7 \\ \underline{7 x - 7} \\ 0. \end{aligned}$
$\begin{align*}&(x-1)\overset{{x\color{red} \quad +7 \quad}}{|\overline{x^2+6x-7}}\\ &\qquad \ \ \ \underline{x^2-x \;\;\; \downarrow \;}\\ & \qquad \qquad \ \ 7x-7\\ &\qquad \quad \underline{\;\;\;\;\; 7x-7 \;}\\ &\qquad \qquad \qquad \ 0.\end{align*}$
:x- 1) x2+6x-7x+7x7x2xx7x7x77x-7_0)

Therefore, $\begin{align*}\frac{x^2+6x-7}{x-1} = x + 7.\end{align*}$
::因此, x2+6x-7x-1=x+7。

Two more examples of long division:
::长期划分的另外两个例子:

$\begin{aligned} \frac{2 x^{2} + 7 x + 5}{2 x + 5} \end{aligned}$
$\begin{align*}\frac{2x^2+7x+5}{2x+5}\end{align*}$
::2x2+7x+52x+5

Step 1: Divide the 1st term in the numerator by the 1st term in the denominator; put this in your answer. Therefore, $\begin{align*}\frac{2x^2}{2x} = x\end{align*}$ .
::步骤 1: 将分子中的第一个词除以分母中的第一个词; 将此写在您的答复中。因此, 2x22x=x。

$\begin{aligned} (2 x + 5) \overset{x}{| \bar{2 x^{2} + 7 x + 5}} \end{aligned}$
$\begin{align*}(2x+5) \overset{{\color{red}x}\qquad \quad}{|\overline{2x^2+7x+5}}\end{align*}$
: 2x+5) @% 2x2+7x5+5x

Step 2: Multiply the denominator by this number (variable) and put it below your numerator, subtract and get your new polynomial:
::第2步:将分母乘以此数(可变)并将其置于分子下方,减去并获得新的多数值 :

$\begin{aligned} (2 x + 5) \overset{x}{| \bar{2 x^{2} + 7 x + 5}} \\ \underline{2 x^{2} + 5 x} \\ 2 x . \end{aligned}$
$\begin{align*}&(2x+5)\overset{{\color{red}x} \qquad \quad}{|\overline{2x^2+7x+5}}\\ &\qquad \quad \underline{2x^2+5x \;\;\;\;\;\;}\\ & \qquad \qquad \ \quad 2x.\end{align*}$
::2x2+7x+5xx2+5x2+5x2+5x2x2x2x2x2x2x2x_2xx2x2x2x2x2x2x5x5x2x2x2x2x2x2x5x2x2x2x2x2x2x2x2x5x2x2x2x2x2x5x2x2x2x2x2x5x2x2x2x5x2x2x2x5x2x2x2x2x5x2x2x2x2x2x2x2x2x2x5x2x2x2x2x2x5x2x2x2x2x5x2x2x2x2x2x2x5x2x2x2x2x2x2x2x5x2x2x2x2x2x2x2x2x5x2x2x2x2x2x2x2x2x2x2x5x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x

Step 3: Repeat the process until you cannot repeat it anymore:
::第3步:在不能再重复之前,重复此进程 :

$\begin{aligned} (2 x + 5) \overset{x + 1}{| \bar{2 x^{2} + 7 x + 5}} \\ \underline{2 x^{2} + 5 x ↓} \\ 2 x + 5 \\ \underline{2 x + 5} \\ 0. \end{aligned}$
$\begin{align*}&(2x+5)\overset{{x\color{red} \quad +1} \quad}{|\overline{2x^2+7x+5}}\\ &\qquad \quad \underline{2x^2+5x \;\; \downarrow \;}\\ & \qquad \qquad \quad \ 2x+5\\ &\qquad \quad \underline{\;\;\;\;\;\;\;\; 2x+5 \;}\\ &\qquad \qquad \qquad \quad 0.\end{align*}$
:2x+5)2x2+7x+5xxx+12x2+5x=2x52x+5_0。

Therefore, $\begin{align*}\frac{2x^2+7x+5}{2x+5}=x+1.\end{align*}$
::因此,2x2+7x+52x+5=x+1。

Last example of long division:
::长分隔的最后一个实例 :

$\begin{aligned} \frac{x^{2} - 5 x + 6}{x - 2} \end{aligned}$
$\begin{align*}\frac{x^2-5x+6}{x-2}\end{align*}$
::x2 - 5x+6x-2

Step 1: Divide the 1st term in the numerator by the 1st term in the denominator, put this in your answer. Therefore, $\begin{align*}\frac{x^2}{x} = x\end{align*}$ .
::第1步:将分子中的第一个术语除以分母中的第一个术语,将其放在您的答复中。因此, x2x=x。

$\begin{aligned} (x - 2) \overset{x}{| \bar{x^{2} - 5 x + 6}} \end{aligned}$
$\begin{align*}(x-2) \overset{{\color{red}x}\qquad \quad}{|\overline{x^2-5x+6}}\end{align*}$
:x-2) x2 - 5x6+6x

Step 2: Multiply the denominator by this number (variable) and put it below your numerator, subtract and get your new polynomial:
::第2步:将分母乘以此数(可变)并将其置于分子下方,减去并获得新的多数值 :

$\begin{aligned} (x - 2) \overset{x}{| \bar{x^{2} - 5 x + 6}} \\ \underline{x^{2} - 2 x} \\ - 3 x . \end{aligned}$
$\begin{align*}&(x-2)\overset{{\color{red}x} \qquad \quad}{|\overline{x^2-5x+6}}\\ &\qquad \ \ \ \underline{x^2-2x \;\;\;\;\;\;}\\ & \qquad \qquad \ \ -3x.\end{align*}$
:x-2)x2 -5x6xxxx2 -2x_-3x)

Step 3: Repeat the process until you cannot repeat it anymore:
::第3步:在不能再重复之前,重复此进程 :

$\begin{aligned} (x - 2) \overset{x - 3}{| \bar{x^{2} - 5 x + 6}} \\ \underline{x^{2} - 2 x ↓} \\ - 3 x + 6 \\ \underline{- 3 x + 6} \\ 0. \end{aligned}$
$\begin{align*}&(x-2)\overset{{x\color{red} \quad -3} \quad \ }{|\overline{x^2-5x+6}}\\ &\qquad \ \ \ \underline{x^2-2x \;\;\; \downarrow \;}\\ & \qquad \quad \ \ -3x+6\\ &\qquad \quad \underline{\;\;\; -3x+6 \;\;}\\ &\qquad \qquad \qquad \ \ 0.\end{align*}$
:x-2) x2 -5x+6x3 x2 -2x=3x6 -3x+6+6_0)

Therefore, $\begin{align*}\frac{x^2-5x+6}{x-2} = x - 3.\end{align*}$
::因此, x2-5x+6x-2=x-3。

Synthetic Division
::合成司

Synthetic division is an alternative to long division. It is a shorthand version of long division when the divisor is a 1st- degree (linear) polynomial. It can also be used to divide a polynomial by a possible factor, $\begin{align*}x - k\end{align*}$ . However, synthetic division cannot be used to divide of a higher degree into another polynomial.
::合成分裂是长分割的替代物,当断层为一度(线性)多元体时,它是一种长分割的速记版本,也可以用来用一个可能的系数(x-k)来将多元体除以。但是,合成分裂不能用来将更高层次的分离分成另一个多元体。

If you are asked to divide $\begin{align*}2x^4-5x^3-14x^2+47x-30\end{align*}$ by $\begin{align*}x - 2\end{align*}$ , you could divide by long division.
::如果您被要求将 2x4- 5x3- 14x2+47x- 30 除以 x-2, 您可以用长的除法分隔。

$\begin{align*}(x-2)\overset{{\color{red} 2x^3 \ \quad -x^2 \ \quad -16x \ \quad+15 \ \ \ } \quad \ }{|\overline{2x^4-5x^3-14x^2+47x-30}}\\ \qquad \ \ \ \underline{\color{blue}2\color{black}x^4-4x^3 \;\;\;\;\; \downarrow \;} \qquad \\ \qquad \qquad \ \color{blue}-1\color{black}x^3-14x^2 \qquad \ \\ \qquad \qquad \ \underline{\;\;\; -x^3+2x^2 \;\;\;\;\;\;\;\;\;\;\;} \ \\ \qquad \qquad \qquad \ \color{blue}-16\color{black}x^2+47x \\ \qquad \qquad \quad \ \ \underline{\;\;\;\;-16x^2+32x \;\;\;\;\;\;\;}\\ \qquad \qquad \qquad \qquad \quad \ \ \ \color{blue}15\color{black}x-30 \ \\ \qquad \qquad \qquad \qquad \quad \ \underline{\;\;\; 15x-30 \;}\\ \qquad \qquad \qquad \qquad \qquad \qquad \ \ \ \color{blue}0 \ \ \\\end{align*}$
:x- 2) *% 2x4 - 5x3 - 5x3 - 14x2+47x- 30 2x3 - x2 - 16x + 15 2x4 - 4x3 * - 1x3 - 14x2 - x3+2x2 - 16x2+47x - 16x2+32x - 15x - 30 15x - 30_ 0)

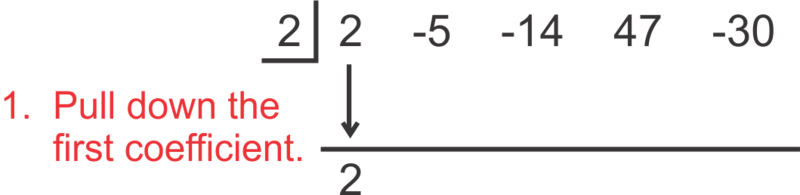
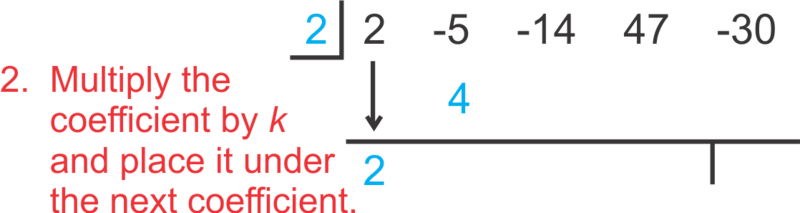
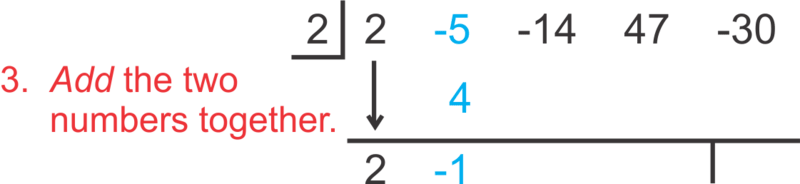
Alternatively, you could use synthetic division. Start by extracting all of your coefficients while also noting the $\begin{align*}k\end{align*}$ from the divisor, $\begin{align*}x-k\end{align*}$ . Then, the setup is as follows:
::或者,您也可以使用合成分解。首先提取所有系数,同时从 dvisor, x-k 中注意 k。然后,设置如下:

To “read” the answer, use the numbers as follows:
::在“阅读”答案时,使用以下数字:

This process shows that $\begin{align*}2x^4-5x^3-14x^2+47x-30=\left(x-2\right)\left(2{x}^{3}-{x}^{2}-16x+15\right)\end{align*}$ , because the remainder is zero. The polynomial $\begin{align*}2x^3-x^2-16x+15\end{align*}$ is read from the bottom row of the synthetic division process. Its degree is one less than the original. We could also write this in division form as:
::此过程显示 2x4- 5x3- 14x3- 14x2+47x- 30=( x-2)( 2x3- x2- 16x+15), 因为剩余部分为零。多元 2x3- x2- 16x+15 是从合成分解过程底行读取的。其程度比原分解少一分。我们还可以用分解形式写成 :

$\begin{aligned} \frac{2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30}{x - 2} \\ = 2 x^{3} - x^{2} - 16 x + 15 + \frac{0}{x - 2} . \end{aligned}$
$\begin{align*}\frac{2x^4-5x^3-14x^2+47x-30}{x-2}\\ =2x^3-x^2-16x+15+\frac{0}{x-2}.\\\end{align*}$
::2x4-5x3-14x2+47-30x-2=2x3-x2-16x+15+0x-2。

$\begin{aligned} T h u s, 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 = (x - 2) (2 x^{3} - x^{2} - 16 x + 15) . \end{aligned}$
$\begin{align*}\mathrm{Thus,} \ 2x^4-5x^3-14x^2+47x-30=(x-2)(2x^3-x^2-16x+15).\end{align*}$
::因此,2x4-5x3-14x2+47x-30=(x-2)(2x3-x2-16x+15)。

Examples
::实例

Example 1
::例1

Divide
::除除

Solution:
::解决方案 :

Step 1: Write the coefficients in an upside-down division sign:
::第1步: 将系数写在上下划线符号中:

Step 2: Put the opposite of the number from the divisor to the left of the division symbol. In this case, the divisor is $\begin{align*}x+1\end{align*}$ , so you will use $\begin{align*}-1\end{align*}$ :
::步数 2: 将数字从 divisor 到 divisor 到 divisor 的左侧。在这种情况下, divisor 是 x+1, 所以您将使用 - 1 :

Step 3: Take your leading coefficient and bring it down below the division symbol:
::第3步:以你的主要系数,将其降到除法符号以下:

Step 4: Multiply this number by the number to the left of the division symbol, and place it in the next column. Add the two numbers together, and place this new number below the division sign:
::第4步:将这个数字乘以除法符号左侧的编号,并将其放在下一列。将两个数字加在一起,并将这个新数字置于除法符号下:

Step 5: Multiply this 2nd number by the number to the left of the division symbol, and place it into the 3rd column. Add the two numbers together, and place this new number below the division sign:
::第5步:将这个第二个数字乘以除法符号左侧的编号,并将其放入第3列。将这两个数字加在一起,并将这个新数字放在除法符号下:

The numbers below the division sign represent your coefficients. Therefore, $\begin{align*}\frac{x^2+3x+2}{x+1}=x+2\end{align*}$ .
::分隔符号下方的数字代表您的系数。因此, x2+3x+2x+1=x+2。

Example 2
::例2

Determine if 4 is a zero of $\begin{align*}5x^3+6x^2-24x-16\end{align*}$ .
::确定 4 是 5x3+6x2 - 24x - 16 的零。

Solution:
::解决方案 :

To determine if 4 is a zero is the same as trying to determine if $\begin{align*}(x-4)\end{align*}$ is a factor. Using synthetic division:
::确定4是否为零与试图确定(x-4)是否是一个因素相同。

The remainder is 304, so $\begin{align*}(x-4)\end{align*}$ is not a factor. Notice that
::其余为304,所以(x-4)不是一个因素。

$\begin{aligned} f (4) = 5 (4)^{3} + 6 (4)^{2} - 24 (4) - 16 = 304. \end{aligned}$
$\begin{align*}f(4)=5(4)^3+6(4)^2-24(4)-16=304.\end{align*}$
::f(4)=5(4)3+6(4)2-24(4)-16=304。

This observation leads to the Remainder Theorem .
::观察结果得出了遗迹定理

Remainder Theorem:
::保留定理 :

If $\begin{align*}f(k) = r\end{align*}$ , then $\begin{align*}r\end{align*}$ is the remainder when dividing $\begin{align*}f(x)\end{align*}$ by $\begin{align*}(x - k)\end{align*}$ . This implies that the point $\begin{align*}(k, r)\end{align*}$ would be on the graph of $\begin{align*}f(x)\end{align*}$ .

Example 3
::例3

Determine if $\begin{align*}2x - 5\end{align*}$ is a factor of $\begin{align*}4x^4-9x^2-100\end{align*}$ .
::确定 2x - 5 是 4x4 - 9x2 - 100 的因数。

Solution:
::解决方案 :

To use synthetic division, the factor must be in the form $\begin{align*}(x - k)\end{align*}$ . The technique to handle this situation is to create a factor with the same zero as $\begin{align*}(2x - 5)\end{align*}$ , which is $\begin{align*}(x - \frac{5}{2})\end{align*}$ . Also, notice that $\begin{align*}4x^4-9x^2-100\end{align*}$ can be written as
::使用合成分除法时,系数必须以(x-k)形式为(x-k)形式。处理这种情况的方法是产生一个与(x-5)(2x-5)相同的零(x-5),即(x-52)。另外,通知4x4-9x2-100可以写成。

$\begin{aligned} 4 x^{4} - 9 x^{2} - 100 = 4 x^{4} + 0 x^{3} - 9 x^{2} + 0 x - 100. \end{aligned}$
$\begin{align*}4x^4-9x^2-100=4x^4+0x^3-9x^2+0x-100.\end{align*}$
::4x4-9x2-100=4x4+0x3-9x2+0x-100。

Since synthetic division is shorthand process, all of these terms must be considered and their coefficients included:
::由于合成分解是短手过程,因此必须考虑所有这些术语,其系数包括:

Therefore, $\begin{align*}\frac{5}{2}\end{align*}$ is a zero and its corresponding binomial , $\begin{align*}2x - 5\end{align*}$ , is a factor. Note that this method confirms that $\begin{align*}2x-5\end{align*}$ is a factor of the polynomial, since the remainder is zero, but it does not tell you the quotient if you were to divide the original polynomial by $\begin{align*}2x-5.\end{align*}$
::因此,52是零,相应的二进制2x-5是一个因素。请注意,这一方法确认2x-5是多元值的一个因素,因为其余部分为零,但如果将原来的多元值除以2x-5,它不会告诉你商数。

Example 4
::例4

Perform the division: $\begin{align*}\frac{3x^3 - 2x^2 + 11x - 9}{x^2 -1} = 3x - 2 + \frac{14x-11}{x^2 -1}.\end{align*}$
::执行分区: 3x3- 2x2+11x- 9x2- 1=3x-2+14x- 11x2- 1。

Solution:
::解决方案 :

To use synthetic division, notice that the factor is not in the form $\begin{align*}(x - k)\end{align*}$ . To find the linear factors , solve $\begin{align*}x^2 -1 = 0\end{align*}$ , to get $\begin{align*}x = 1 \text{ and } -1\end{align*}$ . Therefore, synthetic division can be performed twice because there are two real roots:
::要使用合成分解,请注意该系数不是以(x-k)形式出现的。要找到线性系数,请解析 x2-1=0,以获得 x=1 和-1. 因此,合成分解可以进行两次,因为有两个真正的根:

Next, divide the resulting polynomial, $\begin{align*}3x^2-5x+16\end{align*}$ , with the remainder, $\begin{align*}-25\end{align*}$ , by the other real root , 1:
::其次,将由此形成的3x2-5x+16多边-3x2-5x+16,其余-25除以另一个真正的根,1:

Since the degree of the original dividend polynomial, $\begin{align*}3x^3 - 2x^2 + 11x - 9\end{align*}$ , is 3 and the degree of the divisor polynomial, $\begin{align*}x^2-1\end{align*}$ , is 2, the quotient polynomial is degree 1 because $\begin{align*}3-2=1.\end{align*}$ Therefore, the 3 and $\begin{align*}-2\end{align*}$ from the synthetic division are part of the resulting quotient polynomial, and 14 and $\begin{align*}-11\end{align*}$ from the synthetic division are part of the remainder.
::由于最初的3x3-2x2+11-9红利多股的等级为3,而多股的等级为2,多股的等级为2,多股的商数为1,因为3-2=1.因此,合成部分的3和-2是由此产生的多股的商数的一部分,合成部分的14和-11是其余部分。

Thus, the final answer is $\begin{align*}\frac{3x^3 - 2x^2 + 11x - 9}{x^2 -1} = 3x - 2 + \frac{14x-11}{x^2 -1}.\end{align*}$
::因此,最后答案是3x3-2x2+11x-9x2-1=3x-2+14x-11x2-1。

Example 5
::例5

Divide $\begin{align*}2x^4-11x^3+12x^2+9x-2\end{align*}$ by $\begin{align*}2x + 1\end{align*}$ . Write the resulting polynomial with the remainder (if there is one).
::2x1除以 2x4- 11x3+12x2+9x-2 乘以 2x+1 。将由此产生的多圆形与剩余部分( 如果有的话) 写入。

Solution:
::解决方案 :

To use synthetic division, the factor must be in the form $\begin{align*}(x-k).\end{align*}$ To handle this situation, create a factor with the same zero. In this case, it would be $\begin{align*}\left(x+\frac{1}{2}\right)\end{align*}$ with the zero $\begin{align*}-\frac{1}{2}.\end{align*}$ Do this by factoring out the coefficient of $\begin{align*}x\end{align*}$ in the denominator and dividing the numerator by that number.
::要使用合成分解, 系数必须是表( x- k) 。要处理这种情况, 就必须创建一个相同的零系数。在这种情况下, 系数应该是零 - 12 (x+ 12) 的( X+ 12 ) 。这样做的方法是将分母中的 x 系数乘以x 系数, 并将数字除以该数字。

$\begin{aligned} \frac{(2 x^{4} - 11 x^{3} + 12 x^{2} + 9 x - 2)}{(2 x + 1)} & = \frac{(2 x^{4} - 11 x^{3} + 12 x^{2} + 9 x - 2)}{(2 (x + \frac{1}{2}))} \\ = (\frac{1}{2}) \frac{(2 x^{4} - 11 x^{3} + 12 x^{2} + 9 x - 2)}{(x + \frac{1}{2})} \\ = \frac{(x^{4} - (\frac{11}{2}) x^{3} + 6 x^{2} + (\frac{9}{2}) x - 1)}{(x + \frac{1}{2})} \end{aligned}$
$\begin{align*}\frac{(2x^4 − 11x^3 + 12x^2 + 9x − 2)}{(2x + 1)} &= \frac{(2x^4 − 11x^3 + 12x^2 + 9x − 2)}{\left(2\left(x + \tfrac{1}{2}\right)\right)}\\ &=\left(\frac{1}{2}\right)\frac{(2x^4 − 11x^3 + 12x^2 + 9x − 2)}{\left(x + \tfrac{1}{2}\right)}\\ & = \frac{(x^4 − \left(\tfrac{11}{2}\right)x^3 + 6x^2 + \left(\tfrac{9}{2}\right)x − 1)}{\left(x + \frac{1}{2}\right)}\end{align*}$ Now you can use synthetic division.
:2x4-11x3+12x2+9x2(2x+1)=(2x4-11x3+12x2+9x2)(2(x+12)=(12)(2x4-11x3+12x3+12x2+9x2)(x+12)=(x4-(112)x3+6x2+(92)x-1)(x+12))=(2x4-11x3+12x3+9x2)(x+12)=(x4-(112)x3+6x2+(92)x-1)(x+12)))=(x4-(112)x3+6x2+(92)+1(x+12)))=(2x4x4-11x3+11x3+12)=(2x2x2+9x2)(x2)(x)(x+12)=(x4-(112)x3x3+6x2+2(x1)(x1)(x)(x)(x)(x)(x)(x)(x)(x)x)(x)(x)(x12)))现在你现在可以使用合成分割。

$\begin{align*}\begin{array}{c|rrrrr}{\color{red}\text{-}\tfrac{1}{2}} & 1 & \text{-}\tfrac{11}{2} & 6 & \tfrac{9}{2} &\text{-}1 \\ & \downarrow & \text{-}\tfrac{1}{2} & 3 & \text{-}\tfrac{9}{2} & 0 \\ \hline & 1 & \text{-}6 & 9 & 0 & |\phantom{-} {\color{blue}\text{-}1} \end{array} \end{align*}$

Thus, the answer is $\begin{align*}x^3-6x^2+9x-\frac{1}{x+\tfrac{1}{2}}\end{align*}$ .
::因此,答案是 x3-6x2+9x-1x+12。

Example 6
::例6

Is $\begin{align*}x-6\end{align*}$ a factor, or is 6 a root, of the function $\begin{align*}f(x)=x^3-8x^2+72\end{align*}$ ? If so, find the real roots of the resulting polynomial.
::x- 6 是函数 f( x) =x3- 8x2+72 的因数, 还是 6 是根 ? 如果是的话, 找到结果的多元性的真正根。

Solution:
::解决方案 :

Put a zero placeholder for the $\begin{align*}x-\end{align*}$ term. Divide by 6.
::x- 期数设置一个零占位符。除以 6 。

The resulting polynomial is $\begin{align*}x^2-2x-12\end{align*}$ . While this quadratic does not factor, the quadratic formula is used to find the other roots.
::由此产生的多面性为 x2-2x-12。虽然该二次方块不因子, 却使用二次方块来寻找其他根根。

$\begin{aligned} x = \frac{2 \pm \sqrt{(- 2)^{2} - 4 (1) (- 12)}}{2 (1)} = \frac{2 \pm \sqrt{52}}{2} = \frac{2 \pm 2 \sqrt{13}}{2} = 1 \pm \sqrt{13} \end{aligned}$
$\begin{align*}x=\frac{2 \pm \sqrt{(-2)^2-4(1)(-12)}}{2(1)}=\frac{2 \pm \sqrt{52}}{2}=\frac{2 \pm 2 \sqrt{13}}{2}=1 \pm \sqrt{13}\end{align*}$
::x=2-(-)2-2-4(-)1-1(-)2(1)=2-522=2-2132=1/13

The solutions to this polynomial are 6, $\begin{align*}1+\sqrt{13} \approx 4.61,\end{align*}$ and $\begin{align*}1-\sqrt{13} \approx -2.61\end{align*}$ .
::这一多元性的解决办法是6, 1+134.61和1-132.61。

Example 7
::例7

Divide to prove the following equation true: $\begin{align*}\frac{4{x}^{3}+3{x}^{2}+10x+4}{{x}^{2}+2}=4x + 3 + \frac{2x - 2}{x^2 + 2}.\end{align*}$
::除法以证明下列方程式是真实的: 4x3+3x2+10x+4x2+2=4x3+3+2x-2x2+2。

Solution:
::解决方案 :

The 1st step is to create factors equivalent to $\begin{align*}{x}^{2}+2\end{align*}$ .
::第一个步骤是创造相当于 x2+2 的系数。

$\begin{align*}{x}^{2}+2=0\\x=\pm{i\sqrt{2}}\end{align*}$
::x2+2=0xi2

Using synthetic division, divide by $\begin{align*}i \sqrt{2}\end{align*}$ .
::使用合成分除法,除以i2。

Divide the results from the last step by $\begin{align*}-i \sqrt{2}\end{align*}$ .
::将最后一步的结果除以-i2。

So, $\begin{align*}\frac{4{x}^{3}+3{x}^{2}+10x+4}{{x}^{2}+2}=4x + 3 + \frac{2x - 2}{x^2 + 2}\end{align*}$ .
::所以, 4x3+3x2+10x4x2+2=4x3+2x-2x2+2+2。

Summary
::摘要

Synthetic division is a summary of the long division process. It records the coefficients of the state of a polynomial during the long division process.
::合成分解是长分割过程的概要,记录了长分割过程期间多元状态的系数。

The Remainder Theorem states if $\begin{align*}f(k)=r,\end{align*}$ then $\begin{align*}r\end{align*}$ is the remainder when dividing $\begin{align*}f(x)\end{align*}$ by $\begin{align*}(x-r)\end{align*}$ . This implies that the point $\begin{align*}(k,r)\end{align*}$ would be on the graph of $\begin{align*}f(x)\end{align*}$ .
::留置符定理符表示 f( k) =r, 当 f( x) 除以 ( x) 时, r 是剩余值。这意味着点( k) 将出现在 f( x) 的图形上。

Review
::回顾

Use long division to divide each of the following:
::使用长除法来分隔以下各点:

1. $\begin{align*}(x^2+7x+12)\div(x+3)\end{align*}$
::1. (x2+7x+12) (x+3)

2. $\begin{align*}(x^2+4x+3)\div(x+3)\end{align*}$
::2. (x2+4x+3) (x+3)

3. $\begin{align*}(a^2-4a-45)\div(a-9)\end{align*}$
::3. (a2-4a-45) (a-9)

4. $\begin{align*}(3x^2+5x-2)\div(3x-1)\end{align*}$
::4. (3x2+5x-2)(3x-1)

Use synthetic division to divide the polynomials below. Write out the remaining polynomial:
::使用合成分裂法将多面体分隔在下面。写出其余的多面体 :

5. $\begin{align*}(x^3+6x^2+7x+10) \div (x+2)\end{align*}$
::5. (x3+6x2+7x+10) (x+2)

6. $\begin{align*}(4x^3-15x^2-120x-128) \div (x-8)\end{align*}$
::6. (4x3-15x2-120x-128) (x-8)

7. $\begin{align*}(4x^2-5) \div (2x+1)\end{align*}$
::7. (4x2--5)(2x+1)

8. $\begin{align*}(2x^4-15x^3-30x^2-20x+42) \div (x+9)\end{align*}$
::8. (2x4-15x3-30x2-20x+42)(x+9)

9. $\begin{align*}(x^3-3x^2-11x+5) \div (x-5)\end{align*}$
::9. (x3-3x2-11x+5) (x-5)

10. $\begin{align*}(3x^5+4x^3-x-2) \div (x-1)\end{align*}$
::10. (3x5+4x3-x-2)(x-1)

11. Which of the division problems above generate no remainder? What does that mean?
::11. 以上哪些分裂问题没有剩余?这是什么意思?

12. What is the difference between a zero and a factor?
::12. " 零 " 与 " 因素 " 之间有什么区别?

13. a) Find $\begin{align*}f(-2)\end{align*}$ if $\begin{align*}f(x)=2x^4-5x^3-10x^2+21x-4\end{align*}$ .
::13.a) 如果f(x)=2x4-5x3-10x2+21x-4,则查找 f(-2)。

b) Now, divide $\begin{align*}2x^4-5x^3-10x^2+21x-4\end{align*}$ by $\begin{align*}(x + 2)\end{align*}$ synthetically. What do you notice?
:b) 合成的2x4-5x3-10x2+21x-4除以(x+2)

Find all real zeros of the following polynomials, given one zero:
::查找以下多边形数的所有实际零, 给定为 1 0 :

14. $\begin{align*}12x^3+76x^2+107x-20; \ \text{zero:} \ \text{-}4\end{align*}$
::14. 12x3+76x2+107x-20; 零: - 4

15. $\begin{align*}x^3-5x^2-2x+10; \ \text{zero:} \ 5\end{align*}$
::15. x3-5x2-2x+10;零:5

16. $\begin{align*}6x^3-17x^2+11x-2; \ \text{zero:} \ 2\end{align*}$
::16. 6x3-17x2+11x-2;零:2

Find all real zeros of the following polynomials, given two zeros:
::查找下列多边数的所有实际零, 给定为 2 0 :

17. $\begin{align*}x^4+7x^3+6x^2-32x-32; \ \text{zeros: } \text{-}4, \text{-}1\end{align*}$
::17. x4+7x3+6x2-32x-32;零:4-1

18. $\begin{align*}6x^4+19x^3+11x^2-6x; \ \text{zeros: } 0, \text{-}2\end{align*}$
::18. 6x4+19x3+11x2-6x;零:0,-2

19. The volume of a rectangular prism is $\begin{align*} 3x^3 - 11x^2 - 56x - 48,\end{align*}$ and the height is $\begin{align*}3x + 4\end{align*}$ . What is the area of the base ?
::19. 矩形棱晶体体积为3x3-11x2-56x-48,高度为3x+4。基座的面积是多少?

20. A group of geologists have taken samples of a substance from a proposed mining site and must identify the substance. Each sample is roughly cylindrical. The volume of each sample as a function of cylinder height (in centimeters) is %20%3D%20%5Cfrac%20%7B1%7D%7B4%7D%20%5Cpi%20h%5E3" style="box-sizing: border-box;"> $\begin{align*}V(h) = \frac {1}{4} \pi h^3\end{align*}$ . The mass (in grams) of each sample in terms of height can be modeled by %20%3D%20%5Cfrac%7B1%7D%7B4%7Dh%5E3%20-%20h%5E2%20%2B%205h" style="box-sizing: border-box;"> $\begin{align*}M(h) = \frac{1}{4}h^3 - h^2 + 5h\end{align*}$ . Write an expression that represents the density of the samples. (Hint: $\begin{align*}D = \frac{M}{V}\end{align*}$ )
::20. 一组地质学家从提议的矿址采集了某种物质的样品,必须确定该物质,每个样品大致是圆柱形的,每个样品的体积与气瓶高度(厘米)的函数值是V=14h3. 每一样品的体积(克),从高度来看,可以用M=14h3-h2+5h模拟质量(克)。写一个表示样品密度的表达式。 (Hint:D=MV)

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

3.4 多元体合成部

章节大纲

常规

多多边合成科合成科

Introduction
::导言

Polynomial Long Division
::单体长分区

$\begin{aligned} \frac{x^{2} + 6 x - 7}{x - 1} \end{aligned}$
$\begin{align}\frac{x^2+6x-7}{x-1}\end{align}$
::x2+6x-7x-1

Two more examples of long division:
::长期划分的另外两个例子:

$\begin{aligned} \frac{2 x^{2} + 7 x + 5}{2 x + 5} \end{aligned}$
$\begin{align}\frac{2x^2+7x+5}{2x+5}\end{align}$
::2x2+7x+52x+5

Last example of long division:
::长分隔的最后一个实例 :

$\begin{aligned} \frac{x^{2} - 5 x + 6}{x - 2} \end{aligned}$
$\begin{align}\frac{x^2-5x+6}{x-2}\end{align}$
::x2 - 5x+6x-2

Synthetic Division
::合成司

Examples
::实例

Remainder Theorem:
::保留定理 :

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)

章节大纲

常规

多多边合成科合成科

Introduction ::导言

Polynomial Long Division ::单体长分区

x 2 + 6 x − 7 x − 1 \begin{align*}\frac{x^2+6x-7}{x-1}\end{align*} ::x2+6x-7x-1

Two more examples of long division: ::长期划分的另外两个例子:

2 x 2 + 7 x + 5 2 x + 5 \begin{align*}\frac{2x^2+7x+5}{2x+5}\end{align*} ::2x2+7x+52x+5

Last example of long division: ::长分隔的最后一个实例 :

x 2 − 5 x + 6 x − 2 \begin{align*}\frac{x^2-5x+6}{x-2}\end{align*} ::x2 - 5x+6x-2

Synthetic Division ::合成司

Examples ::实例

Remainder Theorem: ::保留定理 :

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Polynomial Long Division
::单体长分区

$\begin{aligned} \frac{x^{2} + 6 x - 7}{x - 1} \end{aligned}$
$\begin{align}\frac{x^2+6x-7}{x-1}\end{align}$
::x2+6x-7x-1

Two more examples of long division:
::长期划分的另外两个例子:

$\begin{aligned} \frac{2 x^{2} + 7 x + 5}{2 x + 5} \end{aligned}$
$\begin{align}\frac{2x^2+7x+5}{2x+5}\end{align}$
::2x2+7x+52x+5

Last example of long division:
::长分隔的最后一个实例 :

$\begin{aligned} \frac{x^{2} - 5 x + 6}{x - 2} \end{aligned}$
$\begin{align}\frac{x^2-5x+6}{x-2}\end{align}$
::x2 - 5x+6x-2

Synthetic Division
::合成司

Examples
::实例

Remainder Theorem:
::保留定理 :

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)