6.2 特别右三角

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节特别右三角

  折叠 展开

  特别右三角

  播放段落

  Introduction
  ::导言

  播放段落

  The Pythagorean Theorem is a 1st step to start the exploration of trigonometric relationships. There are some special triangles like 45-45-90 and 30-60-90 triangles that are so common that it is useful to know the side ratios without using the Pythagorean Theorem each time. These patterns  are used throughout trigonometry .
  ::Pytagorean Theorem 是开始探索三角关系的第一步。 有些特殊的三角形, 如 45- 45- 90 和 30- 60- 90 三角形非常常见, 不需要每次使用 Pytagorean Theorem 来了解侧比, 就能了解侧比。 这些图案在整个三角测量中都使用 。

  

  播放段落

  Given a 45-45-90 right triangle with sides 6 inches, 6 inches, and  $\begin{array}{r}x\text{inches}\end{array}$ ,  what is the value of   $\begin{array}{r}x\end{array}$ ? 
  ::鉴于一个45-45-90右三角形,侧边6英寸,6英寸和x英寸,x值是多少?

  播放段落

  Special Triangles
  ::特殊三角三角

  播放段落

  45-45-90 Triangles
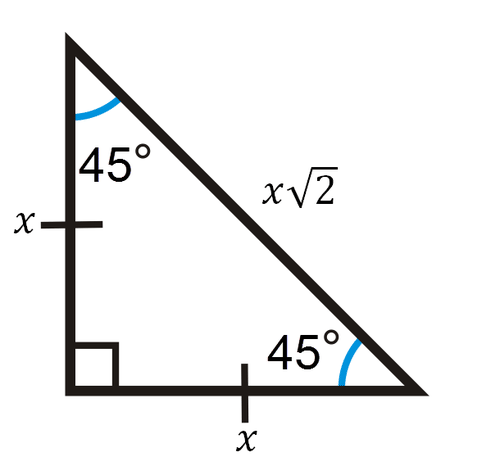
  ::45-45-90三角

  播放段落

  A 45-45-90 right triangle is an isosceles triangle with two sides having the same side length. Let these side lengths be equal to $\begin{array}{r}x\end{array}$ . Use the Pythagorean Theorem to determine the length of the 3rd side. 
  ::右三角45- 45- 90 是一等分形三角形, 两边的侧长相同。 让这些侧长等于 x。 使用 Pytagoren 理论来确定第三边的长度 。

  播放段落

  $$\begin{array}{rl}{x}^2+x^2& =c^2\\ 2x^2& =c^2\\ x\sqrt{2}& =c\end{array}$$

  
  ::x2+x2=c22x2=c2x2=c

  播放段落

  Thus, a 45-45-90 right triangle has side ratios  $\begin{array}{r}x,x,\text{ and }x\sqrt{2}\end{array}$ . 
  ::因此,一个45-45-90右三角有侧比x、x和x2。

  

  播放段落

  30-60-90 Triangles
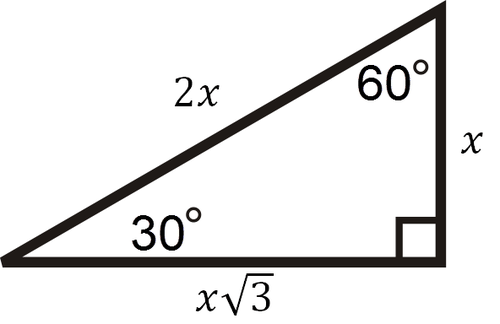
  ::30-60-90三角

   

  播放段落

  A  30-60-90 right triangle has side ratios $\begin{array}{r}x,x\sqrt{3},\text{ and }2x\end{array}$ . 
  ::A 30-60-90右三角有侧翼比率x、x3和2。

  

  
  

  播放段落

  Confirm with the Pythagorean Theorem:
  ::与毕达哥伦神话确认:

  播放段落

  $$\begin{array}{rl}{x}^2+{\left(x\sqrt{3}\right)}^2& =(2x{)}^2\\ x^2+3x^2& =4x^2\\ 4x^2& =4x^2\end{array}$$

  
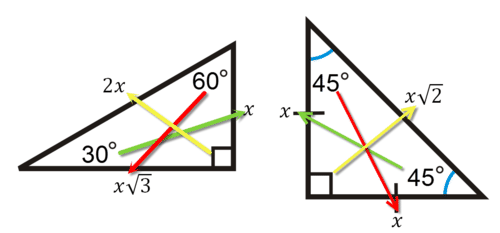
  ::x2+( x3) 2=( 2x) 2x2+3x2=4x24x2=4x2

  播放段落

  Note that the order of the side ratios— $\begin{array}{r}x,x,\text{ and }x\sqrt{2}\end{array}$  and  $\begin{array}{r}x,x\sqrt{3},\text{ and }2x\end{array}$ —is important because each side ratio has a corresponding angle . In all triangles, the smallest sides correspond to the smallest angles, and the largest sides always correspond to the largest angles.
  ::请注意,侧比的顺序 — — x、x、x2和x、x3和2x — — 很重要,因为侧比每个侧比都有相应的角度。 在所有三角中,最小边与最小角度相对应,最大边总是与最大角度相对应。

  

  
  

  播放段落

  The side ratios  for the 45-45-90 right triangle and the  30-60-90 right triangle with examples are also explained in the following video:   
  ::以下视频也解释了45-45-90右三角和30-60-90右三角的侧比,并举例说明:

  播放段落

  Pythagorean Triples
  ::毕达哥里亚三连

  播放段落

  Pythagorean t riples are special right triangles with integral side lengths. While the angle measures are not integers, the side ratios are very useful to know. Here are some examples of :
  ::Pythagorena三重三角形是特殊的右三角形,外长为半边长度。 虽然角度量度不是整数, 但侧比则非常有用。 以下是一些例子 :

  • 3, 4, 5
  • 5, 12, 13
  • 7, 24, 25
  • 8, 15, 17
  • 9, 40, 41

  播放段落

  Additional Pythagorean triples can be found by scaling any other Pythagorean triple . For example,
  ::通过放大任何其他的毕达哥林三联,可以发现其他的毕达哥林三联。例如,

  播放段落

  $\begin{array}{r}3,4,5\to 6,8,10\end{array}$ (scaled by a factor of 2).
  ::3,4,56,8,10(乘以2)

    

  播放段落

  Examples  
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  A right triangle has two sides that are 3 inches in length. What is the length of the 3rd side? 
  ::右三角形的两边长度为3英寸。 第三边的长度是多少?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Since it is a right triangle with  two sides of equal length, then it must be a 45-45-90 right triangle. Thus, the 3rd side is $\begin{array}{r}3\sqrt{2}\text{inches}\end{array}$ .
  ::由于它是右三角形,两边长度相等, 那么它必须是45 - 45 - 90 右三角形。 因此, 第三边是32 英寸 。

  播放段落

  Example 2
  ::例2

  播放段落

  A 30-60-90 right triangle has a hypotenuse of length 10. What are the lengths of the other two sides? 
  ::右三角形30-60-90的长度为10,其他两边的长度是多少?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The hypotenuse is the side opposite the 90°. Sometimes it is helpful to draw a picture or make a table: 
  ::下限是90度对面的一面。 有时绘制图片或制作表格会有所帮助:

  30°	60°	90°
  播放段落 $\begin{array}{r}x\end{array}$ ::x x	播放段落 $\begin{array}{r}x\sqrt{3}\end{array}$ ::x3x3	播放段落 $\begin{array}{r}2x\end{array}$ ::2x 2x
  		10

  播放段落

  From the table, solve the  subsequent equations for the missing sides: 
  ::从表格中解开失踪方程式的后方程式:

  播放段落

  $$\begin{array}{rl}18& =x\sqrt{3}\\ \frac{18}{\sqrt{3}}& =x\\ x& =\frac{18}{\sqrt{3}}=\frac{18}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{18\sqrt{3}}{3}=6\sqrt{3}\\ 2x& =2\cdot 6\sqrt{3}=12\sqrt{3}\end{array}$$

  
  ::18=x3183=xx=183=183=1883=1833=1833=632x=221963=123

  播放段落

  Example 3
  ::例3

  播放段落

  A 30-60-90 right triangle has a side length of 18 inches corresponding to 60 degrees. What are the lengths of the other two sides? 
  ::右三角形30-60-90的侧长为18英寸,相当于60度。其他两边的长度是多少?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Make a table with the side ratios and the information given, then write equations and solve for the missing side lengths: 
  ::绘制带有侧比和所提供信息的表格, 然后写入方程式并解析缺失的侧边长度 :

  30	60	90
  播放段落 $\begin{array}{r}x\end{array}$ ::x x	播放段落 $\begin{array}{r}x\sqrt{3}\end{array}$ ::x3x3	播放段落 $\begin{array}{r}2x\end{array}$ ::2x 2x
  	18

  播放段落

  $$\begin{array}{rl}18& =x\sqrt{3}\\ \frac{18}{\sqrt{3}}& =x\\ x& =\frac{18}{\sqrt{3}}=\frac{18}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{18\sqrt{3}}{3}=6\sqrt{3}\\ 2x& =2\cdot 6\sqrt{3}=12\sqrt{3}\end{array}$$

  
  ::18=x3183=xx=183=183=1883=1833=1833=632x=221963=123

  播放段落

  Note that the denominator is  rationalized so that there is no a square root in the denominator.
  ::请注意,分母是合理化的,以便分母中没有平方根。

  播放段落

  Example 4
  ::例4

  播放段落

  Return to the question in the Introduction. Given a 45-45-90 right triangle with sides 6 inches, 6 inches, and $\begin{array}{r}x\end{array}$  inches, what is the value of $\begin{array}{r}x\end{array}$ ? 
  ::回到导言中的问题。考虑到一个45-45-90右三角形,侧边有6英寸、6英寸和x英寸,x值是多少?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Using  the pattern for , a right triangle with legs 6 inches and 6 inches has a hypotenuse that is $\begin{array}{r}6\sqrt{2}\end{array}$  inches, so  $\begin{array}{r}x=6\sqrt{2}\end{array}$ .
  ::使用此图案, 右三角形有6英寸和6英寸的腿, 下限为62英寸, 所以 x=62 。

  播放段落

  Summary
  ::摘要

  播放段落
  • Corresponding angles and sides are angles and sides that are on opposite sides of each other in a triangle. Capital letters like  $\begin{array}{r}A,B,\text{ and }C\end{array}$ are often used for the angles in a triangle, and the lowercase letters  $\begin{array}{r}a,b,\text{ and }c\end{array}$   are used for their corresponding sides (angle  $\begin{array}{r}A\end{array}$ corresponds to side a, etc.). 
    ::对应角度和侧面是三角形中对立面的角和侧面。 A、B和C等大写字母通常用于三角形中的角,而小写字母a、b和c则用于对应面(角A对面a等)。
  播放段落
  • A 30-60-90 right triangle has side ratios $\begin{array}{r}x,x\sqrt{3},\text{ and }2x\end{array}$ . 
    ::A 30-60-90右三角有侧翼比率x、x3和2。
  播放段落
  • A 45-45-90 right triangle has side ratios $\begin{array}{r}x,x,\text{ and }x\sqrt{2}\end{array}$ . 
    ::A 45-45-90右三角形有侧比x、x和x2。
  播放段落
  • Pythagorean triples are special right triangles with integer sides.  
    ::毕达哥林三重三角形是特殊的右三角形,有整边。

  播放段落

  Review
  ::回顾

  播放段落

  For 1-4, find the missing sides of the 45-45-90 triangle based on the information given in each row:
  ::1-4,根据每行提供的信息,找到45-45-90三角形的缺失侧:

  播放段落 Problem Number ::问题编号	播放段落 Side Opposite $\begin{array}{r}{45}^{\circ }\end{array}$ ::侧面45号对面____________________________________________________________	播放段落 Side Opposite $\begin{array}{r}{45}^{\circ }\end{array}$ ::侧面45号对面____________________________________________________________	播放段落 Side Opposite $\begin{array}{r}{90}^{\circ }\end{array}$ ::90号对面
  1.	3
  2.		7.2
  3.			16
  4.	$\begin{array}{r}5\sqrt{2}\end{array}$

  播放段落

  For 5-8, find the missing sides of the 30-60-90 triangle based on the information given in each row:
  ::对于 5-8, 根据每行提供的信息, 找到 30- 60- 90 三角形的缺失边 :

  播放段落 Problem Number ::问题编号	播放段落 Side Opposite $\begin{array}{r}{30}^{\circ }\end{array}$ ::侧面对面30+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++	播放段落 Side Opposite $\begin{array}{r}{60}^{\circ }\end{array}$ ::侧面对面60	播放段落 Side Opposite $\begin{array}{r}{90}^{\circ }\end{array}$ ::90号对面
  5.	$\begin{array}{r}3\sqrt{2}\end{array}$
  6.		4
  7.			15
  8.			$\begin{array}{r}12\sqrt{3}\end{array}$

   

  播放段落

  Use the picture below for 9-11.
  ::9-11时请使用下图。

  

  播放段落

  9. Which angle corresponds to the side that is 12 units?
  ::9. 哪个角度与12个单位的侧面对应?

  播放段落

  10. Which side corresponds to the right angle?
  ::10. 哪一边与正确角度相对应?

  播放段落

  11. Which angle corresponds to the side that is 5 units?
  ::11. 哪个角度与5个单位的侧面对应?

   

  播放段落

  For 12-17, verify the Pythagorean triple using the Pythagorean Theorem:
  ::使用毕达哥伦神话来验证毕达哥伦三联赛:

  12. 3, 4, 5

  13. 5, 12, 13

  14. 7, 24, 25

  15. 8, 15, 17

  16. 9, 40, 41

  17. 6, 8, 10

   

  播放段落

  18. Find another Pythagorean triple by using the scaling method for 11, 60, 61.
  ::18. 通过使用11,60,61的缩放法,再找一个毕达哥林三联赛。

  播放段落

  Review ( Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。