6.5 科斯定律
章节大纲
-
Introduction
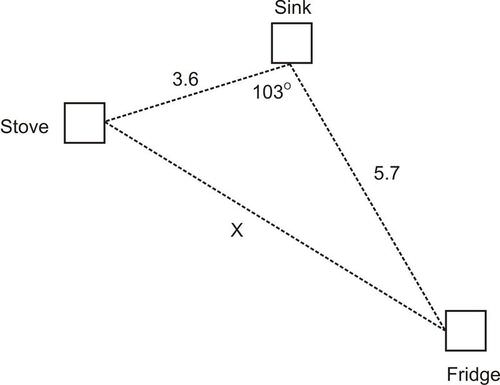
::导言An architect is designing a kitchen for a client. When designing a kitchen, the architect must pay special attention to the placement of the stove, sink, and refrigerator. In order for a kitchen to be utilized effectively, these three amenities must form a triangle with one another, known as the “work triangle.” By design, the three parts of the work triangle must be no less than 3 feet apart and no more than 7 feet apart . Based on the dimensions of the current kitchen, the architect has determined that the sink will be 3.6 feet away from the stove and 5.7 feet away from the refrigerator. If the sink forms a angle with the stove and refrigerator, will the distance between the stove and refrigerator remain within the confines of the work triangle?This question cannot be answered using the right triangle trigonometric relationships because the triangle is not a right triangle. Fortunately, two mathematical laws provide a way to solve the problem. The trigonometric ratios can be extended so they can be used for any type of triangle.
::使用右三角三角三角关系无法解答这个问题, 因为三角不是右三角。 幸运的是, 两个数学法提供了解决问题的方法。 三角比可以扩展, 以便用于任何类型的三角。Derivation of the Law of Cosines
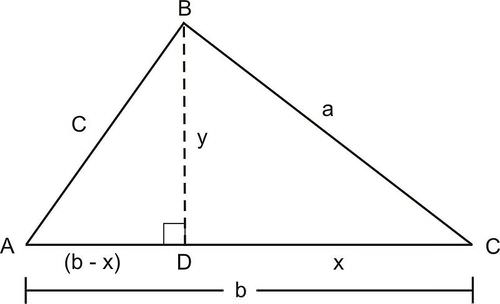
::《科士法》的衍生contains an altitude that extends from and intersects . Refer to the length of as . The sides of measure units, units, and units. If is units long, then measures units.
::ABC 包含从 B 延伸的高度BD, 和相交的 AC 。 参考 BD 的长度 y。 QABC 的侧边测量一个单位、 b 单位和 c 单位。 如果DC x 单位长, 那么AD 计量 (b- x) 单位 。Using the :
::使用:
::c2=y2+(b-x)2Pythagorean Theoremc2=y2+b2-2bx+x2Expand (b-x)2c2=a2+b2-2bxxx2=y2+x2=y2+x2 by Pytagorean Theoremc2=a2+b2-2b(acosC)=cs=xx,因此acsC=x(交叉乘数)c2=a2+b2-2abcos=2x2=y2+x2x2=y2x2=y2=a2+x2=a2cs=a2+cismplilifyUse a similar process to derive all three forms of the :
::使用类似的程序来得出所有三种形式的:
::a2=b2+c2+c2-2bccosAb2=a2+c2-2acosBc2=a2+b2-2abcosCNote that if or is then and the Law of Cosines is identical to the Pythagorean Theorem.
::请注意,如果A,B,或C是 90C,那么900, 和科辛斯定律是完全相同的 匹达哥伦神话。The Law of Cosines is one tool to use in certain situations involving all triangles: right, obtuse, and acute. (Recall that a right triangle is a triangle with one right angle, an obtuse triangle is a triangle with one obtuse angle, and an acute triangle is a triangle with all acute angles.) It is a general statement relating the lengths of the sides of any general triangle to the cosine of one of its angles. There are two situations in which to use the Law of Cosines:
::Casines 定律是用于涉及所有三角形:右三角形、斜角三角形和尖尖三角形的某些情况的一种工具。 (请注意,右三角形是一个右角三角形,斜三角形是一个斜角三角形,尖三角形是一个直角三角形。 )这是一个一般性说明,将任何普通三角形的侧面长度与其角的余弦联系起来。 有两种情况可以使用 Cosines 定律:-
When we know two sides and the included angle in an
oblique triangle
(any triangle that is
not a right
triangle), and we need the 3rd side (SAS).
::当我们了解两面和斜三角形中包含的角度(任何非右三角形的三角形)时,我们需要第三面(SAS)。 -
When we know all three sides in an oblique triangle, and we need one of the angles (SSS).
::当我们知道所有三个方面 在一个斜三角形, 我们需要一个角度(SSS)。
Case 1: Finding the Side of an Oblique Triangle
::案例1:找到一个上方三角形的侧面In this situation, two sides and the included angle in a triangle (SAS) are known and the length of the 3rd side is needed.
::在这种情况下,已知了三角形(SAS)的两面和包括角,需要第三侧的长度。Example 1
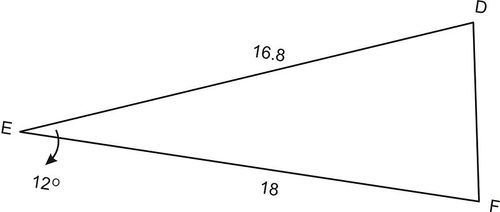
::例1For , let and . Find .
::FORZDEF, let E=12, d=18, f=16.8. find e.Solution:
::解决方案 :Since isn’t a right triangle, the Pythagorean Theorem does not apply. This is an SAS problem, so the Law of Cosines does apply.
::由于“DEF”不是一个右三角,《毕达哥里安理论》不适用。 这是一个SAS问题,因此《科辛斯法》也适用。
::e2=182+16.82-2(18)(16.8)cos12Cosines.e2=324+282.24-2(18)(16.8)cos1212简化正方形.e2324+282.24-591.5836689Multiply.e214.6563311Add,从左到右减去3.8Find平方根。* Note that the negative answer is an extraneous solution, which means it it not a valid solution.
::* 注意否定的回答是一个无关紧要的解决办法,这意味着它不是一个有效的解决办法。Example 2
::例2We can now solve the architect's problem in the Introduction.
::我们现在可以解决建筑师在导言中的问题。Solution:
::解决方案 :To find the distance from the sink to the refrigerator, find side . To find side , use the Law of Cosines because this is an obtuse triangle. We know the lengths of two sides: the sink to the stove and the sink to the refrigerator. We also know that the included angle (the angle between the two known lengths) is . This is an SAS case, so the Law of Cosines applies.
::找到从水槽到冰箱的距离, 找到侧面 x. 找到侧面 x. 使用科辛斯定律, 因为这是一个隐形三角形 。 我们知道两边的长度: 水槽到炉子的长度, 水槽到冰箱的长度。 我们还知道包含的角度( 两个已知长度之间的角)是 103\ 。 这是一个SAS 案例, 因此科辛斯定律适用 。
::x2=3.62+5.72-2.36(5.7)cos103Cosines.x2=12.96+32.49-2.2(3.6)(5.7)cos103简化正方形x212.96+32.49+9.23199127Multiply.x254.68199127Evaluate.x7.4Find 平方根。No, this triangle does not conform to the definition of a work triangle. The sink and the refrigerator are too far apart by 0.4 feet.
::不,这个三角形不符合工作三角形的定义。水槽和冰箱的距离太远了0.4英尺。Case 2: Finding any Angle of a Triangle
::案例2:寻找三角角的任何角Another situation in which the Law of Cosines applies is when all three sides of a triangle are known (SSS), and the measure of one of the angles is needed.
::适用《科辛斯定律》的另一种情况是,三角形的所有三面都已知(SSS),需要测量其中一个角度。Example 3
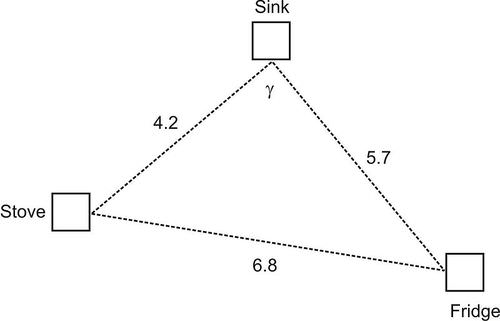
::例3Continuing from Example 2, if the architect moves the stove so it is 4.2 feet from the sink and 6.8 feet from the fridge, how does this affect the angle that the sink forms with the stove and the refrigerator?
::从例2继续,如果建筑师移动炉灶,从水槽到4.2英尺,从冰箱到6.8英尺,这如何影响水槽与炉灶和冰箱形成的角度?Solution:
::解决方案 :To find how the angle is affected, use the Law of Cosines to solve for .
::为了找出角度是如何受到影响的, 使用科辛斯定律解决 。
::6.82=4.22+5.72-2(4.2)(5.7)cos-Lusing Law of Cosines.46.24=17.64+32.49-2(4.2)(5.7)cos-cos-cosimizization plasions.46.24=17.64+32.49-47.88cos_Multiply.46.24=50.1347.88cos-Add.-3.89-88cos_Subtract.0.081244786=cosDivide.cos-1}(0.081244786)=cos-1(cos) ops-1{(cos)采取反向8.53_Simplication。The new angle would be , which means it would be less than the original angle.
::新的角度将是85.3,这意味着比原来的角度少17.7。Example 4
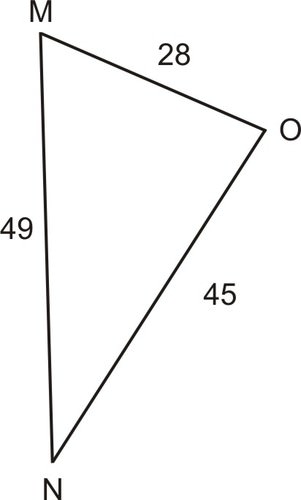
::例4In the oblique and . Find .
::在斜面的 @MNO, m=45,n=28, 和o=49。 找到 @M。Solution:
::解决方案 :Since all three sides of the triangle are known, use the Law of Cosines to find .
::因为三角形的所有三边都已经为人所知,所以使用科辛斯定律来寻找ZM。
::452=282+492-2.28(49cos=Cosines,2,025=784+2,401-2,28(49cos=784+2,401-2,28)(49cos=784+2,401-2,744cos-MMMultiply,2,025=3,185-2,744cos-MAdd.-11602,744CosMSubtract 3,185.4220525=cosómdivide by-2,744.cos-1(0.422740525)=cos-1{(cos-M) 采取反射法65MSimpilation。Example 5
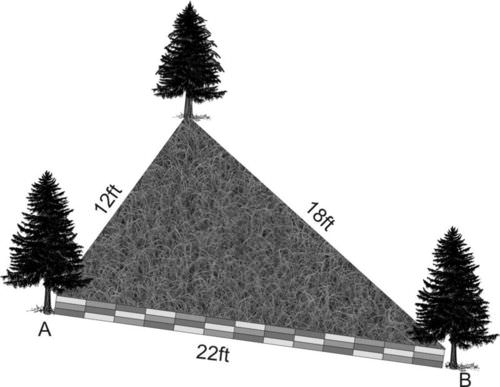
::例5Sam is building a retaining wall for a garden he plans to put in the back corner of his yard. Due to the placement of some trees, the dimensions of his wall need to be as follows: side 1 is 12 feet, side 2 is 18 feet, and side 3 is 22 feet. Determine the angle measure formed by side 1 and side 2, the angle measure formed by side 2 and side 3, and the angle measure formed by side 1 and side 3.
::Sam正在为他计划放置在院子后角的花园建造一座保留墙。 由于设置了一些树木,他的墙的尺寸需要如下:第1边是12英尺,第2边是18英尺,第3边是22英尺。确定第1边和2边形成的角度,第2边和3边形成的角度,以及第1边和3边形成的角度。Solution:
::解决方案 :Since the measures of all three sides of the retaining wall are known, use the Law of Cosines to find the measures of the angles formed by adjacent walls. Refer to the angle formed by side 1 and side 2 as , the angle formed by side 2 and side 3 as , and the angle formed by side 1 and side 3 as . First, find .
::由于保留墙所有三个侧面的措施都是已知的,所以使用《科辛斯定律》来找到相邻墙壁所形成角度的测量尺度。 参考侧1和侧2所形成的角度为 C, 侧2和侧3所形成的角度为 B, 侧1和侧3所形成的角度为 A。 首先, 找到 C。
::222=122+182-2(12)(18cos-Cus-Cuse Law of Cosines. 484=144+324-22(12)(18cos-Cosimplicization squaltiply 484=144+324-432cos-CMULTIly 484=468-432os-432cosCAdd.16<CSubtrapt 468.-0.037037037037cos-CDivide by- 432.cos-1 (0.03703703737)cos-1(cos-C) 采取相反的92.12Cosimpilization。Next, find the measure of also by using the Law of Cosines.
::接下来,通过使用《科辛斯定律》 来找到ZA的量度。
::182=122+222-22(12)(22)cos-Ause Law of Cosines. 324=144+484-2(12)(22)cos-Asitification squals. 324=144+484-528cosçaAMultiply. 324=628-528cosAAdd.-304}528cos*ASubtrole 628.08.575757576=cosçadiide by-528.cos-1 (0.7575757576)=cos-1(cosa) adivide by-528.85_Asimpilation。Now that we know two of the angles, we can find the 3rd angle using the Triangle Sum Theorem, which states that the three angles of a triangle equal 180°.
::现在我们知道其中两个角度了, 我们可以用三角三角SumTheorem 找到第三个角度, 它指出三角形的三个角度等于180°。
::*B=180-(92.12+54.85)=33.03*Identify Accurate Drawings of General Triangles
::识别普通三角形的准确绘图The Law of Cosines can also be used to verify that drawings of oblique triangles are accurate.
::《科辛斯定律》也可以用来核查斜三角形的图画是否准确。Example 6
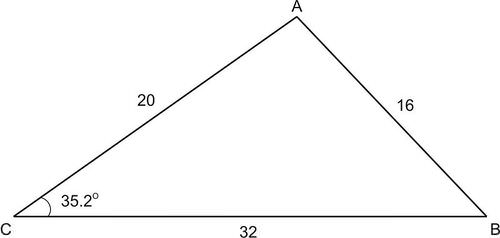
::例6In at the right, , and . Is the drawing accurate if it labels as ? If not, what should measure?
::在“ABC ” 右边的“a= 32,b=20” 和“c=16” 中,“a= 32,b=20” 和“c=16。如果将“C” 标为“35.2” ,那么绘图是否准确?如果没有,那么“C”应该测量什么?Solution:
::解决方案 :Use the Law of Cosines to check whether or not is .
::使用科辛斯定律来检查C是否为35.2。
::162=202+322-2/20(32cos=35.2Cosines 256=400+1,024-2(20) (32cos=35.2Simply places.256400+1,024-1,045.94547Multiply.256378.5453Add和减去。Since , is not . Using the Law of Cosines, calculate the correct measurement of .
::自256378.05453以来,C不是35.2C。使用科辛斯定律计算出C的正确度量。
::162=202+322-2(20)(32cos=CosinesClaw)256=400+1024-2(20)(32cos=Coslimize Squalis256=40000+1024-1280cos@CMultiply256=1424-1280cosCAdd-11681280cos*CSubtrol 14240.9125=CosCDivide24.1Ccos-1(0.9125)For some situations, it is necessary to utilize not only the Law of Cosines, but also the Pythagorean Theorem and trigonometric ratios to verify that a triangle or quadrilateral has been drawn accurately.
::对于某些情况,不仅有必要利用科斯定律,而且有必要利用毕达哥里安理论和三角比,以核实三角或四边形是否准确绘制。Example 7
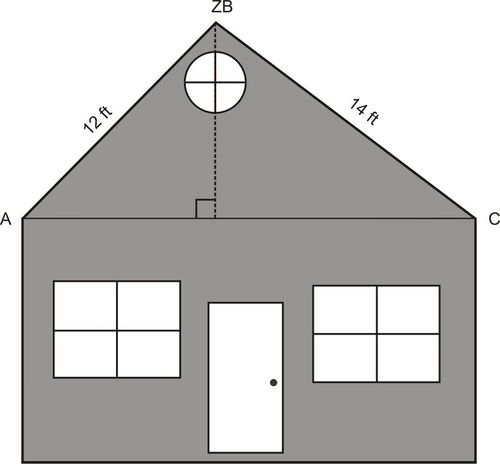
::例7A builder received plans for the construction of a second-story addition on a house. The diagram shows how the architect wants the roof framed, while the length of the house is 20 feet. The builder decides to add a perpendicular support beam from the peak of the roof to the base. He estimates that new beam should be 8.3 feet high, but he wants to doublecheck before he begins construction. Is the builder’s estimate of 8.3 feet for the new beam correct? If not, what is his error?
::建筑商收到了在房屋上建造第二层楼的计划。 图表显示建筑商希望屋顶如何被设计,而房屋的长度是20英尺。 建筑商决定从屋顶的顶峰到基地增加一个垂直的支撑梁。 他估计新梁应该高8.3英尺,但他想在建筑开始之前重复检查。 建筑商对新梁的8.3英尺的估计是否正确? 如果没有,他有什么错误?Solution:
::解决方案 :If either or were known, right triangle trigonometric ratios could be used to find the height of the support beam. However, neither of these angle measures is given. Since all three sides of are known, use the Law of Cosines to find one of these angles. Find :
::如果知道 A 或 C , 右三角三角三角比可以用来找到支持光束的高度。 但是, 却没有给出这些角度的测量。 由于知道 ABC 的所有三面, 使用科辛斯定律来找到其中一个角度 。 find A :
::142=122+202-2(12)(20cosa Ause Law of Cosines. 196=144+400-480cos_480cos_Asimplification. 196=544=484-480cosAAdd.-348480cosAsutrat.0.725=cosAdivide.43.5Acos-1(0.725)Use to find the length of .
::用于查找 BD 的长度 。
::=43.5=x1212sin =43.5=x8.3xYes, the builder’s estimate of 8.3 feet for the support beam is accurate.
::是的,建筑商估计8.3英尺的支撑波束是准确的。Summary
::摘要-
Law of Cosines:
::科斯定律:
::a2=b2+c2+c2-2bccosAb2=a2+c2-2acosBc2=a2+b2-2abcosC-
There are two cases when the Law of Cosines can be applied:
1) When two sides and the included angle in an oblique triangle are known and the 3rd side is needed (SAS).
2) When all three sides in a triangle (SSS) are known and the measure of one of the angles is needed.
::有两种情况可以适用《科辛斯定律》1) 已知两面和斜三角形中包含角的情况,需要第三面(SAS)。 (2) 了解三角形中所有三面的情况,需要测量其中一个角度。
Review
::回顾For , let and .
::ABC,12,b=15,c=20。-
Find
.
::找妈妈吧 -
Find
.
::去找MB -
Find
.
::寻找 mC。
For , let and .
::对于ZZDEF,让我们=25,e=13,f=16。-
Find
.
::去找MD -
Find
.
::去找妈妈 -
Find
.
::去找MF
For , let , and .
::对于KBP,让我们k=19,B=61,p=12。-
Find the length of b.
::查找 b 的长度。 -
Find
.
::去找妈妈 -
Find
.
::寻找 mP。 -
While hiking one day you walk for 5 miles due east, then turn to the left and walk 3 more miles
west of north. At this point you want to return home. How far are you from home if you were to walk in a straight line?
::有一天,你徒步往东走5英里,然后向左转,再往北走3英里30英里。此时,你想要回家。如果你走一条直线,你离家多远? -
A parallelogram has sides of 20 and 31 feet, and an angle of
. Find the length of the longer diagonal of the parallelogram.
::平行图的侧面为 20 和 31 英尺,角度为 46 。 查找平行图的长对角长度 。 -
Dirk wants to find the length of a long building from one side (point A) to the other (point B). He stands outside of the building (at point C), where he is 500 feet from point A and 220 feet from point B. The angle at C is
. Find the length of the building.
::德克希望从一面(A点)到另一面(B点)找到长楼的长度。 他站在大楼外(C点),从A点起500英尺,从B点起220英尺。 C点的角是94。 找到大楼的长度。
Determine whether or not each triangle is possible.
::确定每个三角形是否都可能。-
and
::a=12,b=15,c=10 -
, and
::a=1,b=5,c=4; -
, and
::a=8,b=10,和A=32
Review (Answers)
::回顾(答复)Please see the Appendix.
::请参看附录。 -
When we know two sides and the included angle in an
oblique triangle
(any triangle that is
not a right
triangle), and we need the 3rd side (SAS).