课程： 6.8 基本三角三角三角三角测量应用

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节基本三角三角三角三角基本三角测量应用

折叠展开
基本三角三角三角三角基本三角测量应用
Introduction
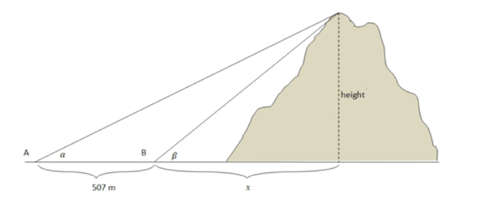
::导言

A surveying crew is given the job of verifying the height of a cliff. From point $\begin{align*}A\end{align*}$ , they measure an angle of elevation to the top of the cliff to be $\begin{align*}\alpha =21.567^\circ\end{align*}$ . They move 507 meters closer to the cliff and find that the angle to the top of the cliff is now $\begin{align*}\beta = 25.683^\circ\end{align*}$ . How tall is the cliff?
::测量组被授予核查悬崖高度的任务。从A点, 他们测量悬崖顶部的高度角为 21.567。他们移动507米接近悬崖, 发现悬崖顶部的角现在是25.683。悬崖有多高?

First, sketch the image and label what you know.
::首先,绘制图像,标上你所知道的标签。

Deciding when to use the right triangle trigonometric functions , or the , is not always obvious. Sometimes more than one approach will work, and sometimes even correct computations can lead to incorrect results. This is because correct interpretation is still essential.
::选择何时使用右三角三角三角函数( 或 ) 并不总是显而易见的。有时不止一种方法会奏效,有时甚至正确的计算也会导致错误的结果。这是因为正确的解释仍然是必不可少的。

Solving Problems Using Right Triangle Trigonometry
::利用右三角三角三角三角解决问题

Right triangles can be used to calculate the angle of elevation or depression in real-world applications. The angle of elevation is the angle at which you view an object above the horizon. The angle of depression is the angle at which you view an object below the horizon. This can be thought of as a negative angle of elevation.
::右三角可以在现实世界应用中用于计算高地或低地角。高地角是您在地平线上查看对象的角度。低地角是您在地平线下查看对象的角度。这可以被视为负高地角。

Bearings in navigation can also be used to determine distances. Bearing is how direction is measured in navigation. On a compass, North is $\begin{align*}0^\circ\end{align*}$ , East is $\begin{align*}90^\circ\end{align*}$ , South is $\begin{align*}180^\circ\end{align*}$ , and West is $\begin{align*}270^\circ\end{align*}$ . For example, a ship traveling at a bearing of $\begin{align*}75^\circ\end{align*}$ is traveling $\begin{align*}75^\circ \end{align*}$ from North towards East. This ship could also be said to be traveling $\begin{align*}90^\circ - 75^\circ =15^\circ \end{align*}$ from East on the compass towards North.
::导航的方位也可以用来确定距离。方位是导航方向的测量方法。方位是北纬0, 东经90, 南纬180, 西经270。例如, 方位为75的船舶正从北经75向东行驶75, 这艘船也可能从东经907515向北行驶。

How to Solve Triangles
::如何解决三角三角

When applying trigonometry, it is important to have a full toolbox of mathematical techniques to use:
::在应用三角测量时,必须有一个完整的数学技术工具箱:

The states that for legs $\begin{align*}a, b\end{align*}$ and hypotenuse $\begin{align*}c\end{align*}$ in a right triangle, $\begin{align*}a^2 + b^2 = c^2\end{align*}$ .
::规定右三角形的腿 a、b 和下角 c, a2+b2=c2。

There are $\begin{align*}360^\circ\end{align*}$ in a circle . N egative angles may need to be re-expressed as positive angles using an angle in this range.
::圆内有 360 。负角度可能需要用此范围中的角度重新表达为正角度。

The three angles in a triangle add up to $\begin{align*}180^\circ\end{align*}$ .
::三角形中的三个角度加起来等于180。

30-60-90 right triangles have side ratios $\begin{align*}x,x\sqrt{3},2x.\end{align*}$
::30-60-90右三角有侧翼比率x,x3,2x。

45-45-90 right triangles have side ratios $\begin{align*}x,x,x\sqrt{2}.\end{align*}$
::45 -45 -90右三角有侧翼比率xxxxxx2。

Pythagorean number triples are exceedingly common and are helpful if recognized in right triangle problems. Examples of triples are 3, 4, 5 and 5, 12, 13.
::Pydagorean数字的三倍非常常见,如果在正确的三角问题中得到承认,会很有帮助,例如,3、4、5和5、12、13是3、4、5和5。

The Triangle Inequality Theorem states that for any triangle, the sum of any two of the sides must be greater than the 3rd side.
::三角不平等理论指出,对于任何三角,任何两边的总和必须大于第三边。

SOH CAH TOA is a mnemonic device to help you remember the three right triangle trig functions:
$\begin{aligned} \sin θ = \frac{o p p}{h y p} \cos θ = \frac{a d j}{h y p} \tan θ = \frac{o p p}{a d j} \end{aligned}$
$\begin{align*}\sin \theta=\frac{opp}{hyp} \quad \cos⁡ \theta = \frac{adj}{hyp} \quad \tan⁡ \theta = \frac{opp}{adj}\end{align*}$
::SOH CHAH TOA 是一个记忆设备, 帮助您记住三个右三角三角三角函数: sinopphypcosadjjhyptanoppadj

The Law of Cosines: $\begin{align*}c^2=a^2+b^2-2ab \cos ⁡C\end{align*}$
::C2=a2+b2-2-2abcosC

The Law of Sines: $\begin{align*}\frac{a}{\sin ⁡A} = \frac{b}{\sin ⁡B}\end{align*}$ or $\begin{align*}\frac{\sin A}{a}=\frac{\sin B}{b}\end{align*}$ ( Consider the Ambiguous Case.)
::Sines法则:asin_A=bsin_B或sin_Aa=sin_Bb(考虑矛盾情况)。

Area Formula: $\begin{align*}\text{Area} = \frac{1}{2} \cdot a \cdot b \sin{C} \end{align*}$
::面积公式: 面积= 12absinC

: $\begin{align*}\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}\end{align*}$ with $\begin{align*}s= \frac{a+b+c}{2}\end{align*}$ .
:::面积=(s-a)(s-b)(s-c),S=a+b+c2。

Examples
::实例

Example 1
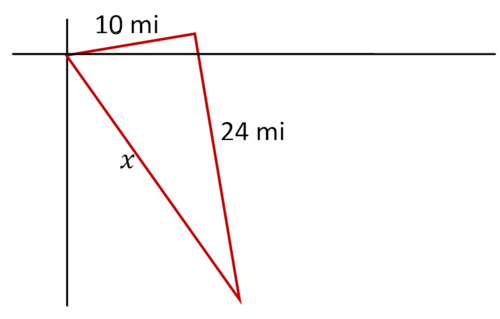
::例1

Bearing is the term used to describe how direction is measured at sea. North is $\begin{align*}0^\circ \end{align*}$ , East is $\begin{align*}90^\circ \end{align*}$ , South is $\begin{align*}180^\circ \end{align*}$ , and West is $\begin{align*}270^\circ \end{align*}$ . A ship travels 10 miles at a bearing of $\begin{align*}88^\circ \end{align*}$ and then turns $\begin{align*}90^\circ \end{align*}$ to the right to avoid an iceberg for 24 miles. How far is the ship from its original position?
::北纬0°C,东经90°C,南纬180°C,西经270°C。一艘船行驶10英里,方位88°C,然后将90°C 转至避冰山24英里的权利。该船离其最初位置有多远?

Solution:
::解决方案 :

First, draw a clear sketch.
::首先,画一个清晰的草图。

Next, recognize the right triangle with legs 10 and 24. This is a multiple of the 5, 12, 13 Pythagorean triple, so the distance $\begin{align*}x\end{align*}$ must be 26 miles.
::接下来,认得右三角形与腿10和24, 这是5,12,13 毕达哥林三重的倍数, 所以距离x必须为26英里。

Example 2
::例2

Returning to the surveyor's question, how tall is the cliff?
::回到测量员的问题悬崖有多高?

Solution:

::解决方案 :

The height is measured at a right angle with the ground. Set up two equations. Remember that $\begin{align*}\alpha\end{align*}$ and $\begin{align*}\beta\end{align*}$ are fixed values, not variables.
::高度与地面以右角测量。设置两个方程式。记住, α 和 β 是固定值, 而不是变量。

$\begin{aligned} \tan α & = \frac{h}{507 + x} \\ \tan β & = \frac{h}{x} \end{aligned}$
$\begin{align*}\tan \alpha & = \frac{h}{507+x}\\ \tan \beta & = \frac{h}{x}\end{align*}$
::tanh507+xtanhx

Solve both of these equations for $\begin{align*}h,\end{align*}$ and then set them equal to each other to find $\begin{align*}x\end{align*}$ .
::解决这两个方程式的h, 然后设定它们等同来找到 x 。

$\begin{aligned} h = \tan α (507 + x) & = x \tan β \\ 507 \tan α + x \tan α & = x \tan β \\ 507 \tan α & = x \tan β - x \tan α \\ 507 \tan α & = x (\tan β - \tan α) \\ x = \frac{507 \tan α}{\tan β - \tan α} & = \frac{507 \tan {21.567}^{\circ}}{\tan {25.683}^{\circ} - \tan {21.567}^{\circ}} \approx 2, 339.997 m \end{aligned}$
$\begin{align*}h= \tan⁡ \alpha (507+x)&=x \tan \beta\\ 507 \tan \alpha+x \tan \alpha&=x \tan ⁡\beta\\ 507 \tan \alpha&= x \tan \beta- x \tan \alpha\\ 507 \tan \alpha&=x(\tan ⁡\beta-\tan \alpha )\\ x= \frac{507 \tan \alpha}{\tan ⁡\beta- \tan \alpha} &= \frac{507 \tan 21.567^\circ}{\tan 25.683^\circ-\tan 21.567^\circ} \approx 2,\!339.997 \text { m}\end{align*}$
:507+xx) =xtan @507+X(507+x) =xtan @507tan(507+x) =507tan}(507+x) =507}(507+x) }(507+x) =(507+x) (507+x) =(507+x) (507+x) =(507+x) (507+x) =(507+x) }(507+x) =(507+x) (507+x) =(507+x) }(507+x) =(507+x) (507+x) (50683) (tan) (215.567) (2,339.997米

Since the problem asked for the height, substitute $\begin{align*}x\end{align*}$ back and solve for $\begin{align*}h\end{align*}$ .
::由于问题要求高度, 替换 x 返回, 并解决h 。

$\begin{align*}h=x \tan \beta = 2339.997 \tan 25.683^\circ \approx 1,\!125.31 \text { m}\end{align*}$
::=xtan 2339.997tan = 25.683 = 1,125.31米

Example 3
::例3

Given a triangle with SSS or SAS, you know how to use the Law of Cosines. In triangles where there are corresponding angles and sides like AAS or SSA, it makes sense to use the Law of Sines. What about ASA?
::鉴于SSS或SAS的三角形,你知道如何使用Cosines定律。在有AAS或SASA等相应角度和侧面的三角形中,使用Sines定律是有道理的。 ASA呢?

Given $\begin{align*}\Delta ABC\end{align*}$ with $\begin{align*}A= \frac{\pi}{4} \text{ radians}, C = \frac{\pi}{6} \text{ radians}\end{align*}$ , and $\begin{align*}b=10 \text{ in}\end{align*}$ . What is $\begin{align*}a\end{align*}$ ?
::以 A 4 弧度、 C 6 弧度和 b = 10 英寸的 ABC 表示。什么是 ?

Solution:
::解决方案 :

First, draw a picture.
::首先,画一张图。

The sum of the angles in a triangle is $\begin{align*}180^\circ \end{align*}$ . Since this problem is in radians, convert each angle to degrees.
::三角形中角度的总和是 180\\\\\。由于这个问题是以弧度为单位, 请将每个角度转换为度。

$\begin{aligned} A & = \frac{π}{4} \cdot \frac{180^{\circ}}{π} = 45^{\circ} \\ C & = \frac{π}{6} \cdot \frac{180^{\circ}}{π} = 30^{\circ} \end{aligned}$
$\begin{align*}A & = \frac{\pi}{4} \cdot \frac{180^\circ}{\pi} = 45^\circ\\ C & = \frac{\pi}{6} \cdot \frac{180^\circ}{\pi} = 30^\circ\end{align*}$
::418045C683030

The missing angle must be $\begin{align*}\angle B=105^\circ\end{align*}$ . Now use the Law of Sines to solve for $\begin{align*}a\end{align*}$ .
::缺失的角度必须是 {B=105\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\B=105\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"Sines定律解决一个。"

$\begin{aligned} \frac{\sin 105^{\circ}}{10} & = \frac{\sin 45^{\circ}}{a} \\ a & = \frac{10 \sin 45^{\circ}}{\sin 105^{\circ}} \approx 7.32 in \end{aligned}$
$\begin{align*}\frac{\sin 105^\circ}{10} & = \frac{\sin 45^\circ}{a}\\ a&= \frac{10 \sin 45^\circ}{\sin 105^\circ} \approx 7.32 \text { in}\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Example 4
::例4

Sometimes when using the Law of Sines, you find the results are not consistent with the Law of Cosines. Both answers can be correct computationally, but the Law of Sines may require further analysis when the triangle is obtuse. The Law of Cosines does not require this 2 nd step.
::有时当使用Sines定律时,你会发现结果与Cisines定律不符。两个答案都可以计算正确,但当三角形模糊时,Sines定律可能需要进一步分析。 Cisines定律并不要求第二步。

First, use the Law of Cosines to find $\begin{align*}\angle B\end{align*}$ .
::首先,使用科辛斯定律来找到"B"

$\begin{aligned} 12^{2} & = 3^{2} + 14^{2} - 2 \cdot 3 \cdot 14 \cdot \cos B \\ ∠ B & = \cos^{- 1} (\frac{12^{2} - 3^{2} - 14^{2}}{- 2 \cdot 3 \cdot 14}) \approx {43.43}^{\circ} \end{aligned}$
$\begin{align*}12^2&=3^2+14^2-2 \cdot 3 \cdot 14 \cdot \cos B\\ \angle B &= \cos^{-1} \left ( \frac{12^2-3^2-14^2}{-2 \cdot 3 \cdot 14} \right ) \approx 43.43^\circ \end{align*}$
::122=32+142-231414BBB=Cos-11(122-32-142-2314)434343

Next, use the Law of Sines to find $\begin{align*}\angle C\end{align*}$ . Use the unrounded value for $\begin{align*}B,\end{align*}$ even though a rounded value is shown.
::接下来,使用辛那斯定律来查找 C. 使用 B 的未四舍五入值, 即使显示四舍五入值。

$\begin{aligned} \frac{\sin {43.43}^{\circ}}{12} & = \frac{\sin C}{14} \\ \frac{14 \sin {43.43}^{\circ}}{12} & = \sin C \\ ∠ C & = \sin^{- 1} (\frac{14 \sin {43.43}^{\circ}}{12}) \approx {53.3}^{\circ} \end{aligned}$
$\begin{align*}\frac{\sin 43.43^\circ}{12}&= \frac{\sin C}{14}\\ \frac{14 \sin 43.43^\circ}{12} & = \sin C\\ \angle C &=\sin^{-1} \left ( \frac{14 \sin 43.43^\circ}{12} \right ) \approx 53.3^\circ\end{align*}$
:14sin43.4312) (53.33)

Use the Law of Cosines to doublecheck $\begin{align*}\angle C\end{align*}$ .
::使用科辛斯定律来重复检查ZC

$\begin{aligned} 14^{2} & = 3^{2} + 12^{2} - 2 \cdot 3 \cdot 12 \cdot \cos C \\ C & = \cos^{- 1} (\frac{14^{2} - 3^{2} - 12^{2}}{- 2 \cdot 3 \cdot 12}) \approx {126.7}^{\circ} \end{aligned}$
$\begin{align*}14^2&=3^2+12^2-2 \cdot 3 \cdot 12 \cdot \cos C\\ C & = \cos^{-1} \left ( \frac{14^2-3^2-12^2}{-2 \cdot 3 \cdot 12} \right ) \approx 126.7^\circ\end{align*}$
::142=32+122-2312cCC=cos-1(142-32-122-2312)126.7

Notice that the last two answers do not match, but they are supplementary. This is because this triangle is obtuse, and the $\begin{align*}\sin^{-1} \left ( \frac{opp}{hyp} \right )\end{align*}$ function is restricted to only producing acute angles. Don't forget to check for the ambiguous case when using the Law of Sines.
::请注意后两个答案不匹配, 但它们是补充性的。这是因为三角形是模糊的, 而 sin - 1 (opphyp) 函数仅限于生成急性角度。在使用 Sines 法则时, 不要忘记检查模糊性。

Example 5
::例5

From the 3rd story of a 50-foot building, someone observes a car driving on the street below towards the building. If the angle of depression of the car changes from $\begin{align*}21^\circ\end{align*}$ to $\begin{align*}45^\circ\end{align*}$ while the person watches, how far did the car travel?
::从一个50英尺高的建筑的第3个故事,有人看到一辆汽车在下面的街上向大楼行驶。如果汽车的压抑角度从21英寸到45英寸高,当人们看着时,车走多远?

Solution:
::解决方案 :

Draw a very clear picture.
::画一个非常清晰的图片。

In the upper right corner of the picture, four important angles are marked. The measures of these angles from the outside in are $\begin{align*}90^\circ, 45^\circ, 21^\circ, 69^\circ\end{align*}$ . There is a 45-45-90 right triangle on the right, so the base must also be 50. Therefore, set up and solve an equation for $\begin{align*}x\end{align*}$ .
::在图片的右上角标记了四个重要角度。这些角度从外部的测量为 90 , 45, 21, 69。右侧有一个45- 45- 90 的右三角, 因此基数也必须是 50 。因此, 设置并解析 x 的方程式。

$\begin{aligned} \tan 69^{\circ} & = \frac{x + 50}{50} \\ x & = 50 \tan 69^{\circ} - 50 \approx 80.25 ft \end{aligned}$
$\begin{align*}\tan 69^\circ & = \frac{x + 50}{50}\\ x & = 50 \tan 69^\circ - 50 \approx 80.25 \text { ft}\end{align*}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Often, the hardest parts of this problem are drawing a picture and working with the angles.
::这一问题中最困难的部分往往是绘制图象和以角度开展工作。

Example 6
::例6

If a boat travels 4 miles SW and then 2 miles NNW, how far away is it from its starting point?
::如果一艘船行驶在南纬4英里处,再行行驶2英里西北,它离起点有多远?

Solution:
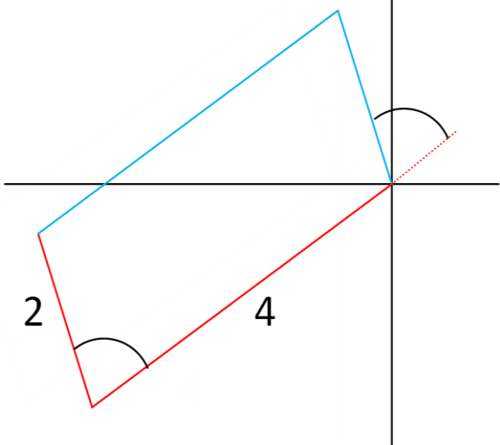
::解决方案 :

Translate SW and NNW into degrees-bearing. SW is a bearing of $\begin{align*}225^\circ,\end{align*}$ and NNW is a bearing of 337.5°. Draw a picture in two steps. Draw the original 4 miles traveled, and draw the 2nd 2 miles traveled from the origin. Then translate the 2nd leg of the trip so it follows the 1st leg. This way you end up with a parallelogram, which has interior angles that are easier to calculate.
::将 SW 和 NNNW 转换为度承承。 SW 是 225 的轴承, NNW 是 337. 5 的轴承。绘制一张两步的图片。绘制最初的 4 英里 , 绘制从原点起行的 2 英里。然后翻译旅行的第二段, 这样它就可以沿着第 1 条。这样一来, 你就会看到一个平行的图, 其内角比较容易计算。

The angle between the two red line segments is $\begin{align*}67.5^\circ,\end{align*}$ which can be seen if the red line is extended past the origin and you find the complement of the difference between the two bearings.
::两条红线段之间的角是67.5,如果红线的长度超过源头,你就会发现两个轴线之间的差数的补充。

$\begin{aligned} 180^{\circ} - ({337.5}^{\circ} - 225^{\circ}) = {67.5}^{\circ} \end{aligned}$
$\begin{align*}180^\circ - (337.5^\circ -225^\circ) = 67.5^\circ\end{align*}$

The shorter diagonal of the parallelogram is the required unknown information.
::180(337.5225)=67.5 平行图的短对角是所需的未知信息。

$\begin{aligned} x^{2} & = 4^{2} + 2^{2} - 2 \cdot 4 \cdot 2 \cdot \cos {67.5}^{\circ} \\ x & \approx 3.7 m \end{aligned}$
$\begin{align*}x^2 & = 4^2 + 2^2 - 2 \cdot 4 \cdot 2 \cdot \cos 67.5^\circ\\ x & \approx 3.7 \text { m}\end{align*}$
::x2=42+22-2422255x3.7米

Summary
::摘要

When working with triangles, numerous mathematical techniques can be used, including trigonometry.
::当与三角形合作时,可以使用许多数学技术,包括三角测量法。

Angle of elevation is the angle at which you view an object above the horizon.
::高度角是您在地平线上查看对象的角度。

Angle of depression is the angle at which you view an object below the horizon. This can be thought of as a negative angle of elevation.
::抑郁角是您在地平线下观察对象的角度。这可以被视为负高角。

Bearing is how direction is measured in navigation . North is $\begin{align*}0^\circ\end{align*}$ , East is $\begin{align*}90^\circ\end{align*}$ , South is $\begin{align*}180^\circ,\end{align*}$ and West is $\begin{align*}270^\circ\end{align*}$ .
::北纬0°C,东经90°C,南纬180°C,西经270°C。

Review
::回顾

The angle of depression of a boat in the distance from the top of a lighthouse is $\begin{align*}\frac{\pi}{6}\end{align*}$ . The lighthouse is 150 feet tall. Find the distance from the base of the lighthouse to the boat.
::与灯塔顶部相距的一艘船的压抑角度是 6。灯塔有150英尺高。寻找灯塔底部至船的距离。

1. Draw a picture of this situation.
::1. 描绘一下这种情况。

2. What methods or techniques will you use?
::2. 你会使用何种方法或技术?

3. Solve the problem.
::3. 解决问题。

From the 3rd story of a building (60 feet), Jeff observes a car moving towards the building driving on the streets below. The angle of depression of the car changes from $\begin{align*}34^\circ\end{align*}$ to $\begin{align*}62^\circ\end{align*}$ while he watches. How far has the car traveled?
::Jeff从第3个建筑(60英尺)的故事中看到一辆汽车在下面的街道上向大楼行驶。汽车的压抑角度在他看着的时候从34英寸变为62英寸。车走多远了?

4. Draw a picture of this situation.
::4. 描绘一下这种情况。

5. What methods or techniques will you use?
::5. 你会使用何种方法或技术?

6. Solve the problem.
::6. 解决问题。

A boat travels 6 miles NW and then 2 miles SW. You want to know how far away the boat is from its starting point.
::一艘船行驶6英里长,然后2英里长。你想知道船离起点有多远。

7. Draw a picture of this situation.
::7. 描述一下这种情况。

8. What methods or techniques will you use?
::8. 你会使用何种方法或技术?

9. Solve the problem.
::9. 解决问题。

You want to figure out the height of a building. From point $\begin{align*}A\end{align*}$ , you measure an angle of elevation to the top of the building to be $\begin{align*}\alpha = 10^\circ\end{align*}$ . You move 50 feet closer to the building to point $\begin{align*}B\end{align*}$ , and find that the angle to the top of the building is now $\begin{align*}\beta = 60^\circ\end{align*}$ .
::您想要弄清楚建筑物的高度。从 A点, 您测量建筑物顶部的高度角为 10 。您将离建筑物更近50英尺的角移动到 B点, 并发现大楼顶部的角现在是 60 。

10. Draw a picture of this situation.
::10. 描绘一下这种情况。

11. What methods or techniques will you use?
::11. 你会使用何种方法或技术?

12. Solve the problem.
::12. 解决问题。

13. Given $\begin{align*}\Delta ABC\end{align*}$ with $\begin{align*}A = 40^\circ, C = 65^\circ\end{align*}$ and $\begin{align*}b=8 \text { in}\end{align*}$ , what is $\begin{align*}a\end{align*}$ ?
::13. 鉴于A=40,C=65,B=8,A=40,C=65,B=8,什么是A?

14. Given $\begin{align*}\Delta ABC\end{align*}$ with $\begin{align*}A = \frac{\pi}{3} \text { radians, } C = \frac{\pi}{8} \text { radians}\end{align*}$ and $\begin{align*}b = 12 \text { inches}\end{align*}$ what is $\begin{align*}a\end{align*}$ ?
::14. 具有A3弧度、C8弧度和b=12英寸A=3弧度的ABC=12英寸A=3弧度、C8弧度和B=12英寸B=12英寸A=12

15. Given $\begin{align*}\Delta ABC\end{align*}$ with $\begin{align*}A = \frac{\pi}{6} \text { radians, } C = \frac{\pi}{4} \text { radians}\end{align*}$ and $\begin{align*}b = 20 \text { inches}\end{align*}$ what is $\begin{align*}a\end{align*}$ ?
::15. 以A6弧度、C4弧度和b=20英寸的A=6弧度ABC计算,

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

章节大纲

常规

基本三角三角三角三角基本三角测量应用

Introduction ::导言

Solving Problems Using Right Triangle Trigonometry ::利用右三角三角三角三角解决问题

How to Solve Triangles ::如何解决三角三角

Examples ::实例

Example 5 ::例5

Example 6 ::例6

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Solving Problems Using Right Triangle Trigonometry
::利用右三角三角三角三角解决问题

How to Solve Triangles
::如何解决三角三角

Examples
::实例

Example 5
::例5

Example 6
::例6

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)