7.2 单位圆圈

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节联合圆圈

  折叠 展开

  联合圆圈

  播放段落

  Introduction 
  ::导言

  播放段落

  The unit circle is a circle of radius 1 that is centered at the origin.
  ::单位圆是半径 1 的圆, 以原点为中心 。

  

  播放段落

  Sketch the central angle (θ) in standard position . This angle is formed by the $\begin{align*}x\end{align*}$ -axis, the origin, and the terminal side of the angle. Its terminal side intersects the unit circle at  $\begin{align*}\left(x,y\right).\end{align*}$  Since the radius is one,  $\begin{align*}\cos{\theta} = \frac{x}{1} = x \end{align*}$  and  $\begin{align*}\sin{\theta} = \frac{y}{1} = y\end{align*}$ . Thus, $\begin{align*}\left(x,y\right)=\left(\cos\theta, \sin\theta\right).\end{align*}$   
  ::在标准位置中绘制中心角 。 此角由角度的 X 轴、 源头和终端侧组成。 其终端侧面在 (x, y) 处交叉单位圆。 由于半径为 1, CO=x1=x 和 siny1=y 。 因此, (x,y) = (cosQ, sin+) 。

  播放段落

  This framework makes it easy to  evaluate expressions like $\begin{align*}\cos (135^\circ)\end{align*}$  or $\begin{align*}\sin \left(-\frac{5 \pi}{3}\right)\end{align*}$ . It also helps to produce the parent graphs of . 
  ::此框架便于评价 cos( 135) 或 sin( 5) 等表达式, 也有助于生成 . 的母形图 。

  播放段落

  Reference Angles
  ::参考角度

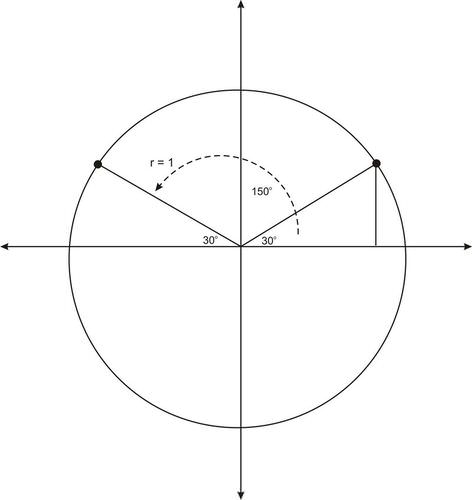
  播放段落

  Consider the angle $\begin{align*}150^\circ\end{align*}$ . With this angle in standard position, the terminal side of this angle is a reflection ( across the $\begin{align*}y-\end{align*}$ axis) of an angle with terminal side of $\begin{align*}30^\circ\end{align*}$ .
  ::考虑角度 150\\\ 。 以这个角度为标准位置, 这个角度的终点是角度的反射( 横跨 y- 轴) , 末端为 30\ \ 。

  

  播放段落

  Notice that in the preceding figure, the terminal side of the  $\begin{align*}150^\circ\end{align*}$  angle makes a $\begin{align*}30^\circ\end{align*}$ angle with the negative $\begin{align*}x-\end{align*}$ axis. Therefore,  $\begin{align*}30^\circ\end{align*}$ is the nonnegative  reference angle for $\begin{align*}150^\circ\end{align*}$ .
  ::请注意,在上图中,150角的末端面为30角,带有负 x- 轴。因此,30是150的非负参考角。

  播放段落

  Formally, the reference angle of an angle in standard position is the angle formed with the terminal side of the angle, and the part  of the $\begin{align*}x-\end{align*}$ axis closest to the terminal side.
  ::在形式上,一个角度在标准位置上的参考角是角度末端和最接近终点端的 x- 轴部分所形成的角。

  播放段落

  Notice that $\begin{align*}30^\circ\end{align*}$ is the reference angle for many angles. For example, it is the reference angle for $\begin{align*}210^\circ\end{align*}$ and for $\begin{align*}-30^\circ\end{align*}$ .  Since the coordinates of the point on the terminal side of $\begin{align*}30^\circ\end{align*}$  and the unit circle are  $\begin{align*}\left(\cos 30 ^{\circ}, \sin 30^{\circ}\right) = \left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)\end{align*}$ , the corresponding reflected point of the terminal side of  $\begin{align*}150^\circ\end{align*}$  is  $\begin{align*}\left(\cos 150 ^{\circ}, \sin 150^{\circ}\right) = \left(-\frac{\sqrt{3}}{2},\frac{1}{2}\right).\end{align*}$
  ::注意 30\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Identifying the reference angle for an angle is used to determine the values of the trig functions of the angle. Once the reference angle is graphed, a right  triangle can be drawn using the reference angle and the $\begin{align*}x-\end{align*}$ axis. The values of the trigonometric functions of the angle can then be determined using the resulting reference triangle.
  ::确定角的参考角用于确定角的三角函数值。一旦绘制了参考角图,就可以使用参考角和 x- 轴绘制右三角。然后,可以使用由此生成的参考三角确定角的三角函数值。

   

  播放段落

  Create the Unit Circle for Special Angles
  ::为特殊角度创建单圆圆

  播放段落

  To be ready to completely fill in a unit circle, we need to review two special triangles. Start by finding the side lengths of a 30-60-90 triangle and a 45-45-90 triangle, each with a hypotenuse equal to 1.
  ::要准备完全填满一个单位圆, 我们需要检查两个特殊的三角。 首先找到一个30- 60- 90三角和一个45- 45- 90三角的侧长, 每个三角的下限等于 1 。

  $\begin{align*}30^\circ\end{align*}$	$\begin{align*}60^\circ\end{align*}$	$\begin{align*}90^\circ\end{align*}$
  $\begin{align*}x\end{align*}$	$\begin{align*}x \sqrt{3}\end{align*}$	$\begin{align*}2x\end{align*}$
  $\begin{align*}\frac{1}{2}\end{align*}$	$\begin{align*}\frac{\sqrt{3}}{2}\end{align*}$	1

  $\begin{align*}45^\circ\end{align*}$	$\begin{align*}45^\circ\end{align*}$	$\begin{align*}90^\circ\end{align*}$
  $\begin{align*}x\end{align*}$	$\begin{align*}x\end{align*}$	$\begin{align*}x \sqrt{2}\end{align*}$
  $\begin{align*}\frac{\sqrt{2}}{2}\end{align*}$	$\begin{align*}\frac{\sqrt{2}}{2}\end{align*}$	1

  播放段落

  This is enough information to fill out the important points in the 1st quadrant of the unit circle.  The values of the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -coordinates for each of the key points are shown below. Remember that the $\begin{align*}x\end{align*}$ - and $\begin{align*}y\end{align*}$ -coordinates come from the lengths of the legs of the special right triangles, as shown specifically for the $\begin{align*}30^\circ\end{align*}$  angle. The hypothenuse of any right triangle in the unit circle is the same length as the radius of the unit circle, $\begin{align*}r=1\end{align*}$ . Always remember to measure the angle from the positive portion of the $\begin{align*}x\end{align*}$ -axis.
  ::此信息足以填充单位圆第1象值中的重要点。 以下显示每个关键点的 x 和 y 坐标值。 记住, x 和 y 坐标来自特殊右三角的腿长, 具体显示为 30 角 。 单位圆中任何右三角的假设值与单位圆半径相同, r= 1 。 记住要从 X 轴正轴部分测量角 。

  

  播放段落

  Knowing the 1st quadrant well is the key to knowing the entire unit circle.  Every other point on the unit circle can be found by reflecting the values in the 1st quadrant.
  ::了解第1象限井是了解整个单位圆的关键。单位圆的每一个点都可以通过反映第1象限中的值而找到。

   

    

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Graph each angle and identify its reference angle.
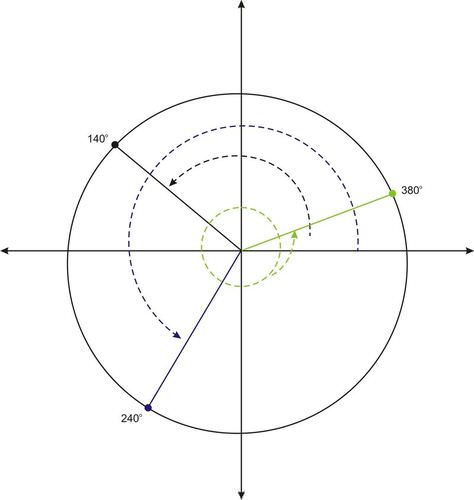
  ::绘制每个角度的图表,并标明其参考角度。

  播放段落

  a. $\begin{align*}140^\circ\end{align*}$
  ::a. 140_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}140^\circ\end{align*}$ makes a $\begin{align*}40^\circ\end{align*}$ angle with the negative $\begin{align*}x-\end{align*}$ axis. Therefore, the reference angle is $\begin{align*}40^\circ\end{align*}$ .
  ::140 以负 x - 轴为40 角。 因此, 参考角为 40 。

  播放段落

  b. $\begin{align*}240^\circ\end{align*}$
  ::b. 240_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}240^\circ\end{align*}$ makes a $\begin{align*}60^\circ\end{align*}$  angle with the negative $\begin{align*}x-\end{align*}$ axis. Therefore, the reference angle is $\begin{align*}60^\circ\end{align*}$ .
  ::240 . 因此,

  播放段落

  c. $\begin{align*}380^\circ\end{align*}$
  ::c. 380__________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}380^\circ\end{align*}$ is a full rotation of $\begin{align*}360^\circ,\end{align*}$  plus an additional $\begin{align*}20^\circ\end{align*}$ . So this angle is coterminal with $\begin{align*}20^\circ\end{align*}$ , and $\begin{align*}20^\circ\end{align*}$ is its reference angle.
  ::380琌360锣 20 ┮硂àcm20琌妓 20琌参旧à

  播放段落

  Graph for a, b, and c:
  ::a、b和c的图表:

  

   

  播放段落

  Example 2
  ::例2

  播放段落

  Use the 1st quadrant of the unit circle to identify the angles and important points of the 2nd quadrant. 
  ::使用单位圆的第1象限来识别第2象限的角和重要点。

  播放段落

  Solution: 
  ::解决方案 :

  播放段落

  The heights are equal and  correspond to the  $\begin{align*}y\end{align*}$ -values. The  $\begin{align*}x\end{align*}$ -values are all negative.
  ::高度相等,与 Y 值相对应。 x 值均为负值。

  

    

  播放段落

  Example 3
  ::例3

  播放段落

  Identify a pattern in the heights of the points in the 1st quadrant as a memory device . 
  ::将第1象限点高度的图案标记为内存设备。

  播放段落

  Solution: 
  ::解决方案 :

  播放段落

  The heights of the points in the 1st quadrant are the $\begin{align*}y\end{align*}$ -coordinates, which are  $\begin{align*}0, \frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, 1.\end{align*}$
  ::第1象限点的高度是Y坐标,是0,12, 22, 32,1。

  播放段落

  When rewritten, the pattern becomes clear: $\begin{align*}\frac{0}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}\end{align*}$ .
  ::改写后,图案变得清晰:02, 12, 22, 32, 42。

  播放段落

  The three points in the middle are the most often confused . This pattern illustrates how they increase in size from small $\begin{align*}\frac{1}{2}\end{align*}$ , to medium $\begin{align*}\frac{\sqrt{2}}{2}\end{align*}$ , to large $\begin{align*}\frac{\sqrt{3}}{2}\end{align*}$ .  When completing the unit circle, look for the heights that are small, medium, and large to position trig  values correctly. Notice that the heights for these five points in the 2nd quadrant are also $\begin{align*}0, \frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, 1\end{align*}$ .
  ::中间的三点最经常混淆。 这个模式显示了它们从小12点到中22点,到大32点的大小。 当完成单位圆时, 寻找小、 中、 大的高度来正确定位三角值 。 请注意, 第二象限中这五点的高度也是 0, 12, 22, 32, 1 。

  

    

  播放段落

  This technique also works for the widths. This can make memorizing the 16 points of the unit circle a matter of reflecting  the pattern: $\begin{align*}\frac{0}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}\end{align*}$ .
  ::这一技术也用于宽度,可以使单位圆的16点被记住,成为反映图案的一件事:02, 12, 22, 32, 42。

  播放段落

  Example 4
  ::例4

  播放段落

  Evaluate $\begin{align*}\cos 60^\circ\end{align*}$  using the unit circle and . What is the connection between the  $\begin{align*}x\end{align*}$ -coordinate of the point and the cosine of the angle? 
  ::使用单位圆和 。 点的 x 坐标与角的连结之间有什么联系 ?

  播放段落

  Solution:  
  ::解决方案 :

  播放段落

  The point on the unit circle for $\begin{align*}60^\circ\end{align*}$  is $\begin{align*}\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right),\end{align*}$  and the point is 1 unit from the origin. This can be represented as a 30-60-90 triangle.
  ::60 单位圆的点为 12 32 , 点为 原点的 1 个单位 。 这可以作为 30- 60- 90 三角形表示 。

  

  播放段落

  Since cosine is adjacent over hypotenuse, cosine turns out to be exactly the  $\begin{align*}x\end{align*}$ coordinate $\begin{align*}\frac{1}{2}\end{align*}$ .
  ::由于连弦在低温上空相邻,因此,连弦正好是X座标12。

  播放段落

  Example 5
  ::例5

  播放段落

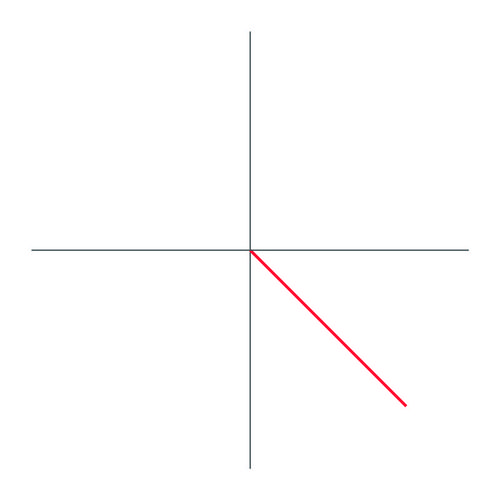
  Graph $\begin{align*}315^\circ\end{align*}$ and identify its reference angle. Find  $\begin{align*}\sin 315^ \circ.\end{align*}$
  ::图315* 并标明其参考角度。 查找 sin315* 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The graph of $\begin{align*}315^\circ\end{align*}$  is as follows:
  ::315图如下:

  

  播放段落

  Since the angle makes a $\begin{align*}45^\circ\end{align*}$ angle with the positive $\begin{align*}x\end{align*}$ -axis, the reference angle is $\begin{align*}45^\circ\end{align*}$ . Using the unit circle, the ordered pair associated with  $\begin{align*}315^{\circ}\end{align*}$  is  $\begin{align*}\left(\frac{\sqrt2}{2}, -\frac{\sqrt2}{2}\right),\end{align*}$  so  $\begin{align*}\sin315^{\circ}=-\frac{\sqrt2}{2}\end{align*}$   in standard position.
  ::由于角度为正 X 轴的 45 角, 参考角度为 45 。 使用单位圆, 315 的定购配对是 (22, 22) , 所以标准位置为 sin315 22 。

  播放段落

  Example 6
  ::例6

  播放段落

  Find the ordered pair on the unit circle for $\begin{align*}150^\circ\end{align*}$ and use it to find the value of $\begin{align*}150^\circ\end{align*}$ .
  ::查找单位圆上150的定购一对,并用它来找到150的值。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1: Identify that the reference angle is $\begin{align*}30^\circ\end{align*}$ .
  ::第1步:确定参考角为30。

  播放段落

  Step 2: Determine the coordinates for the point on the unit circle are $\begin{align*}\left( -\frac{\sqrt{3}}{2},\frac{1}{2} \right) \end{align*}$ .
  ::第2步:确定单位圆上点的坐标(32,12)。

  播放段落

  Step 3: Substitute:
  ::第3步:替代:

  播放段落

  $$\begin{align*} \cos 150^\circ = \frac{\text{adjacent side}}{\text{hypotenuse}} = \frac{-\frac{\sqrt{3}}{2}}{1} = -\frac{\sqrt{3}}{2} \end{align*}$$
  ::近邻的侧侧日冕 321 32

  播放段落

  Example 7
  ::例7

  播放段落

  Evaluate the following trigonometric expressions using the unit circle. Remember:  $\begin{align*}\csc\left(-\frac{5 \pi}{4}\right)=\frac{1}{\sin{\left(-\frac{5 \pi}{4}\right)}}=\frac{2}{\sqrt{2}}=\sqrt{2}\end{align*}$
  ::使用单位圆评价以下三角数表达式 。 记住: csc( - 54) = 1sin( - 54) = 22 @ @ 2

  播放段落

  a.  $\begin{align*}\sin \frac{\pi}{2}\end{align*}$
  ::a. 罪2

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}\sin \frac{\pi}{2}=1\end{align*}$
  ::sin2=1

  播放段落

  b.  $\begin{align*}\cos 210^\circ\end{align*}$
  ::b. COs210_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}\cos 210^\circ=-\frac{\sqrt{3}}{2}\end{align*}$
  ::CO210 32

  播放段落

  c. $\begin{align*}\tan 315^\circ\end{align*}$
  ::c. tan315___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}\tan 315^\circ=-1\end{align*}$
  ::tan3151

  播放段落

  d.  $\begin{align*}\cot 270^\circ\end{align*}$
  ::d. COT270___________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}\cot 270^\circ=0\end{align*}$
  ::科特2700

  播放段落

  e.  $\begin{align*}\sec \frac{11 \pi}{6}\end{align*}$
  ::e. 秒11+6

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}\sec \frac{11 \pi}{6}=\frac{1}{\cos \frac{11 \pi}{6}}=\frac{2}{\sqrt{3}}=\frac{2 \sqrt{3}}{3}\end{align*}$
  ::秒11=1cos11=6=23=233

  播放段落

  f.  $\begin{align*}\csc - \frac{5 \pi}{4}\end{align*}$
  ::f. csc-54

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $\begin{align*}\csc\left(-\frac{5 \pi}{4}\right)=\frac{1}{\sin{\left(-\frac{5 \pi}{4}\right)}}=\frac{2}{\sqrt{2}}=\sqrt{2}\end{align*}$
  ::csc(- 54) = 1sin(- 54) = 2222

  播放段落

  Summary
  ::摘要

  播放段落
  • The unit circle is a circle with its center at the origin and with a radius of 1, whose equation is  $\begin{align*}{x}^{2}+{y}^{2}=1\end{align*}$ .  
    ::单位圆是一个圆形,其中心位于原点,半径为1,其方程式为 x2+y2=1。
  播放段落
  • A central angle is the angle formed by two radii of the circle intersecting the circle.
    ::中心角是圆圆交错的两个弧形所形成的角。
  播放段落
  • The reference angle  of an angle in standard position is the angle formed between the terminal side and the closest portion of the  $\begin{align*}x-\end{align*}$ axis. 
    ::在标准位置上角的参考角是终端侧与 x- 轴最接近部分之间形成角。
  播放段落
  • Since coterminal angles end at identical points along the unit circle, trigonometric expressions involving coterminal angles are equivalent: $\begin{align*}\sin{\left(-10^\circ\right)}=\sin 350^\circ = \sin 710^\circ\end{align*}$ .  
    ::由于共同终点角在单位圆的相同点结束,涉及共同终点角的三角数表达式相当:sin(-10)=sin350sin710。

   

  

  播放段落

  Review
  ::回顾

  播放段落

  Name an angle between  $\begin{align*}0^\circ\end{align*}$ and  $\begin{align*}360^\circ\end{align*}$ that is coterminal with the given angle:
  ::命名 0 和 360 之间的角, 以给定角为共同终点 :

  1. $\begin{align*}-20^\circ\end{align*}$

  2. $\begin{align*}475^\circ\end{align*}$

  3. $\begin{align*}-220^\circ\end{align*}$

  4. $\begin{align*}690^\circ\end{align*}$

  5. $\begin{align*}-45^\circ\end{align*}$

  播放段落

  Use your knowledge of the unit circle to help determine whether the  trigonometric expression is positive or negative:
  ::使用您对单位圆的了解来帮助确定三角表达式是正或负:

  播放段落

  6.  $\begin{align*}\tan 143^\circ\end{align*}$
  ::6. tan143_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  7. $\begin{align*}\cos \frac{\pi}{3}\end{align*}$
  ::7 COs%3 , 7 COs%3

  播放段落

  8. $\begin{align*}\sin 362^\circ\end{align*}$
  ::第8362号罪

  播放段落

  9. $\begin{align*}\csc \frac{3 \pi}{4}\end{align*}$
  ::9. csc34

  播放段落

  Use your knowledge of the unit circle to evaluate the trigonometric expression:
  ::使用您对单位圆的了解来评价三角表达式:

  播放段落

  10.  $\begin{align*}\cos 120^\circ\end{align*}$
  ::10. COS120__________________________________________________________________________________________________________________________

  播放段落

  11. $\begin{align*}\sec \frac{\pi}{3}\end{align*}$
  ::11 秒=3

  播放段落

  12. $\begin{align*}\tan 225^\circ\end{align*}$
  ::12. 坦 坦 225 __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  13. $\begin{align*}\cot 120^\circ\end{align*}$
  ::13. COT120______________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  14. $\begin{align*}\sin \frac{11 \pi}{6}\end{align*}$
  ::14. 罪行11 6

  播放段落

  15. $\begin{align*}\csc 240^\circ\end{align*}$
  ::15 csc240

  播放段落

  16. Draw the complete unit circle (all four quadrants) and label the important points.
  ::16. 绘制完整的单位圆(全部四个四方圆)并标出重要点。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。