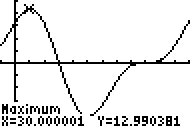7.8 三角函数的应用

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节三角函数的应用

  折叠 展开

  三角函数的应用

  播放段落

  Introduction
  ::导言

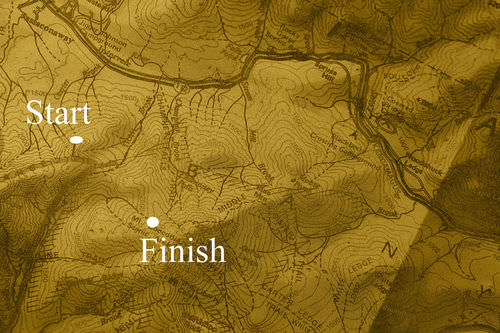
  播放段落

  On a sunny spring day, you decide to map out a hiking trip to a new spot in the state park near your home. According to your map, you are supposed to go on a course that ends with you having moved 2.5 miles east and 3 miles south. Your starting and finishing points on your map are shown here:
  ::在一个阳光明媚的春天,你决定去你家附近的州公园的一个新地方远足旅行。根据你的地图,你应该走上一条路线,最后你向东移动了2.5英里,向南移动了3英里。你的地图上的起点和终点在这里显示:

  

  
  

  播放段落

  Now you need to calculate the angle you need to walk with respect to due east. Can you find a way to calculate this angle using ?
  ::现在您需要计算您需要向东方向行走的角度。 您可以找到一个方法来计算这个角度 ?

  播放段落

  Applying Trigonometric Functions   
  ::应用三角函数

  播放段落

  The following are real-world problems that can be solved using the trigonometric functions . In everyday life, indirect measurement is used to obtain answers to problems that are impossible to solve using measurement tools. However, mathematics will come to the rescue in the form of trigonometry to calculate these unknown measurements.
  ::下面是使用三角函数可以解决的现实世界问题。 在日常生活中,间接测量被用于获得无法用测量工具解决问题的答案。然而,数学将以三角测量法的形式被拯救,以计算这些未知的测量数据。

  播放段落

  On a cold winter day, the sun streams through your living room window, creating a warm, toasty atmosphere. This is due to the angle of inclination of the sun, which directly affects the heating and cooling of buildings. At noon, the sun is at its maximum height in the sky, with the angle greater in the summer than in the winter. Because of this, buildings are constructed so that the overhang of the roof shades the windows for cooling in the summer, and yet allows sun rays to provide heat in the winter. The angle of inclination of the sun varies according to the latitude of the building’s location.
  ::在寒冷的冬天,太阳从客厅窗户流过,形成温暖的烤烤气氛,这是由太阳倾角造成的,直接影响到建筑物的供暖和冷却。 中午,太阳在天空的最高高度,夏季的倾角大于冬季。 因此,建筑物的建造使屋顶的顶部遮盖了夏季的窗户以冷却,同时又允许太阳照射在冬天提供热。 太阳的倾角因建筑物位置的纬度而异。

  播放段落

  If the latitude of the location is known, the following formula can be used to calculate the angle of inclination of the sun on any given date of the year:
  ::如果知道位置的纬度,可使用下列公式计算每年任何特定日期太阳倾角角:

  播放段落

  $\begin{array}{r}\text{Angle of sun}={90}^{\circ }-\text{latitude}+-{23.5}^{\circ }\cdot \cos \left[(N+10)\frac{360}{365}\right],\end{array}$ where $\begin{array}{r}N\end{array}$ represents the number of the day of the year that corresponds to the date of the year. Note: This formula is accurate to $\begin{array}{r}\pm \frac{1^{\circ }}{2}.\end{array}$
  ::太阳角=90latitude23.5cos[((N+10)360365),其中N表示与当年日期对应的当年天数。注意:这个公式精确到%12。

  播放段落

  Determine the measurement of the sun’s angle of inclination for a building located at a latitude of $\begin{array}{r}{42}^{\circ }\end{array}$ , March $\begin{array}{r}10,\end{array}$  the $\begin{array}{r}69th\end{array}$ day of the year.
  ::确定位于年3月10日即年年第69天42度纬度的建筑物的太阳倾角的测量。

  播放段落

  $$\begin{array}{rl}\text{Angle of sun}& ={90}^{\circ }-{42}^{\circ }+-{23.5}^{\circ }\cdot \cos \left[(69+10)\frac{360}{365}\right]\\ \text{Angle of sun}& ={48}^{\circ }+-{23.5}^{\circ }(0.2093)\\ \text{Angle of sun}& ={48}^{\circ }-{4.92}^{\circ }\\ \text{Angle of sun}& ={43.08}^{\circ }\end{array}$$

  
  ::太阳的角=904223.5cos[(69+10)360.365] 太阳的角=4823.5(0.2093) 太阳的角=484.92太阳的角=43.08

  播放段落

  Determine the measurement of the sun’s angle of inclination for a building located at a latitude of $\begin{array}{r}{20}^{\circ }\end{array}$ , September $\begin{array}{r}21\end{array}$ .
  ::9月21日,确定位于纬度20°Z的建筑物的太阳倾角的度量。

  播放段落

  $$\begin{array}{rl}{\theta }_2& =\theta -{\theta }_1\\ \tan \theta & =\frac{10}{x}\text{and}\tan {\theta }_1=\frac{3}{x}\\ {\theta }_2& ={\tan }^{-1}\left(\frac{10}{x}\right)-{\tan }^{-1}\left(\frac{3}{x}\right)\end{array}$$

  
  ::21tan10x 和 tan1= 3x2= tan-1(10x)-tan-1(3x)

  播放段落

  Note that i f you didn't know the day of the year and had to find the day given the angle of the sun, you would need to use inverse cosine to solve.
  ::请注意,如果你不知道 一年的一天, 并不得不找到的日子 以太阳的角度, 你需要使用反余弦 来解决。

  播放段落

  Another application example can be seen in the following video:
  ::以下视频中可以看到另一个应用实例:

   

     

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  A 28.4-foot tower must be secured with a guy-wire anchored 5 feet from the base of the tower. What angle will the guy-wire make with the ground?
  ::一座28.4英尺高的塔必须用一条人电固定在离塔底5英尺的地方。

  播放段落

  Solution:
  ::解决方案 :

  

  播放段落

  $$\begin{array}{rl}\tan \theta & =\frac{opp.}{adj.}\\ \tan \theta & =\frac{28.4}{5}\\ \tan \theta & =5.68\\ {\tan }^{-1}(\tan \theta )& ={\tan }^{-1}(5.68)\\ \theta & ={80.02}^{\circ }\end{array}$$

  
  ::tanopp.adj.tan 28,45tan 5,68tan -1 (tan) =tan -1 (5.68) 80.02

  播放段落

  Example 2
  ::例2

  播放段落

  Note that the following problem that involves functions and their inverses will be solved using the property $\begin{array}{r}f(f^{-1}(x))=f^{-1}(f(x))\end{array}$ .
  ::请注意,下列涉及功能及其反向的问题将使用财产f(f-1(x)=f-1(f)(x))解决。

  播放段落

  In the main concourse of the local ice arena, several viewing screens are available to watch so you don't miss any of the action on the ice. The bottom of one screen is 3 feet above eye level, and the screen itself is 7 feet high. The angle of vision (inclination) is formed by looking at both the bottom and top of the screen.  Calculate the measure of the angle of vision that results from looking at the bottom and then the top of the screen. At what distance from the screen does the maximum value for the angle of vision occur?
  ::在本地冰场的主汇合处, 有几个屏幕可供观看, 这样您不会错过冰上的任何动作。 一个屏幕的底部是眼睛水平的3英尺, 屏幕本身是7英尺高。 视觉角度( 倾角) 是通过查看屏幕的底部和顶部而形成的。 计算视觉角度的度量, 该角度来自屏幕的底部和顶部。 距离屏幕的距离会给视觉角度带来最大值吗 ?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Sketch a picture to represent this problem:
  ::绘制一个图片来代表这个问题:

  

  播放段落

  $$\begin{array}{rl}{\theta }_2& =\tan \theta -\tan {\theta }_1\\ \tan \theta & =\frac{10}{x}\text{and}\tan {\theta }_1=\frac{3}{x}\\ {\theta }_2& ={\tan }^{-1}\left(\frac{10}{x}\right)-{\tan }^{-1}\left(\frac{3}{x}\right)\end{array}$$

  
  ::2 = tan 1tan10x 和 tan1 = 3x2 = tan-1 (10x)- tan-1 (3x)

  播放段落

  To determine these values, use a graphing calculator and the trace function to determine when the actual maximum occurs.
  ::为确定这些值,使用图形计算器和跟踪函数来确定实际最大值何时发生。

  

  播放段落

  From the graph, we can see that the maximum occurs just before  $\begin{array}{r}x\approx 5.59ft\end{array}$  and $\begin{array}{r}{\theta }_2\approx {32.57}^{\circ }\end{array}$ . If you calculate the actual maximum there, it is approximately 5.477 at 32. 58°.
  ::从图中可以看出,最大值发生在 x5.59英尺和232.57英寸之前。如果计算实际最大值,则在32.58°时约为5.477。

  播放段落

  Example 3
  ::例3

  播放段落

  A carnival Ferris wheel with a radius of 14 m makes one complete revolution every 16 seconds. The bottom of the wheel is 1.5 m above the ground. If a person is at the top of the wheel when a stopwatch is started, how high above the ground will that person be after 1 minute and 7 seconds?
  ::半径为14米的嘉年华飞轮每16秒就发生一次彻底革命。 轮底部在地面上1.5米。 如果有人在轮顶上, 当一个站岗手表启动时, 这个人在地面上方, 1分7秒后会有多高 ?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  is 14 m.
  ::14时。

  播放段落

  Since the Ferris wheel completes one revolution every 16 seconds, 
  ::自从费利斯轮每16秒完成一次革命

  播放段落

  $$\begin{array}{r}b=\frac{{360}^{\circ }}{16}=\mathrm{22.5.}\end{array}$$

  
  ::b=36016=22.5。

  播放段落

  There is no horizontal shift for this problem, so  $\begin{array}{r}h=0\end{array}$ . 
  ::这个问题没有水平变化, 所以 h=0 。

  播放段落

  The vertical shift is the radius of the Ferris wheel, plus the distance the wheel is from the ground. 
  ::垂直移动是Ferris轮的半径, 加上方向盘与地面的距离。

  播放段落

  $$\begin{array}{r}k=14+1.5=15.5\text{ m}\end{array}$$

  The resulting equation is  $\begin{array}{r}y=14\cos \left(22.5(x+0\right)+\mathrm{15.5.}\end{array}$
  ::k=14+1.5=15.5 m 生成的方程式为y=14cos(22.5(x+0)+15.5。

  播放段落

  In this problem,  $\begin{array}{r}x=67\text{ s}\end{array}$ , so with the angle in degrees,
  ::在此问题中, x=67 s, 所以用角度以度计,

  播放段落

  $$\begin{array}{rl}y& =14\cos \left(22.5(67)\right)+15.5\\ y& =20.86\text{ m}.\end{array}$$

  Thus, the person on the Ferris wheel will be 20.86 m above the ground after 1 minute and 7 seconds.   
  ::y=14cos(22.5(67)+15.5y=20.86m.因此,Ferris轮上的人在1分7秒后将超过地面20.86m。

  播放段落

  Example 4
  ::例4

  播放段落

  Recall the problem from the Introduction: You are planning a hiking trip and have to calculate the angle you need to walk with respect to due east. 
  ::回顾导言中的问题:你正在计划徒步旅行,并且必须计算需要步行到东端的角。

  播放段落

  Solution:
  ::解决方案 :

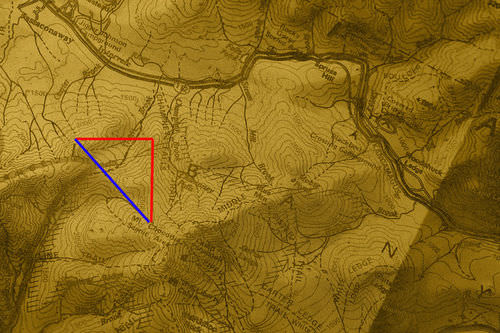
  播放段落

  You can set up a triangle that matches the physical situation of this problem. Here's what it should look like:
  ::您可以设置一个三角形, 这个三角形与这个问题的物理环境相匹配。 以下是它应该的样子 :

  

  
  

  播放段落

  Using the tangent function, you can solve for the angle you need to find:
  ::使用正切函数,您可以解析您需要找到的角 :

  播放段落

  $$\begin{array}{r}\theta ={\tan }^{-1}\left(\frac{-3}{2.5}\right)\\ \theta =-{50.19}^{\circ }\end{array}$$

  
  ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 50.19 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

  播放段落

  Example 5
  ::例5

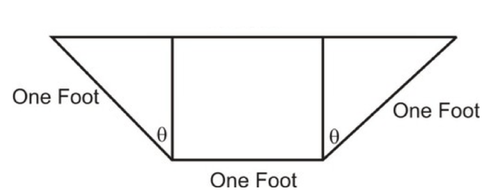
  播放段落

  The diagram below represents the end of a water trough. The ends are actually isosceles trapezoids, and the length of the trough from end to end is 10 feet. Determine the maximum volume of the trough and the value of $\begin{array}{r}\theta \end{array}$ that maximizes that volume.
  ::下面的图表代表了水槽的尽头。 末端实际上是等骨类类, 而从尽头到尽头的槽长度是 10 英尺。 确定槽的最大体积和最大体积的 ° 值 。

  

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The volume is 10 feet times the area of the end. The end consists of two congruent right triangles and one rectangle. The area of each right triangle is $\begin{array}{r}\frac{1}{2}(\sin \theta )(\cos \theta ),\end{array}$ and that of the rectangle is $\begin{array}{r}(1)(\cos \theta )\end{array}$ . This means the volume can be determined by the function $\begin{array}{r}V(\theta )=10(\cos \theta +\sin \theta \cos \theta )\end{array}$ . This function can be graphed as follows to find the maximum volume and the angle $\begin{array}{r}\theta \end{array}$ where it occurs:
  ::音量是末端面积的10英尺。 末端由两个相匹配的右三角形和一个矩形组成。 每个右三角形的面积是 12 (sin) (cos) , 矩形的面积是 (1)(cos) 。 这意味着音量可以由函数 V () = 10 (cossinçççç) 来决定。 此函数可以如下图绘制, 以查找最大音量和角 。

  

  播放段落

  Therefore, the maximum volume is approximately 13 cubic feet and occurs when $\begin{array}{r}\theta \end{array}$ is about $\begin{array}{r}{30}^{\circ }\end{array}$ . 
  ::因此,最大体积约为13立方英尺,当 约30立方英尺时发生。

  播放段落

  Review
  ::回顾

  播放段落
  1. The distance from a boat to a lighthouse is 100 feet, and the lighthouse is 120 feet tall. What is the angle of depression from the top of the lighthouse to the boat?
     ::从船到灯塔的距离是100英尺,灯塔是120英尺高。 灯塔从灯塔顶部到船头的压抑角度是什么?
  播放段落
  2. You are standing 100 feet from an arch that is 68 feet tall. At what angle do you have to look up to see the top of the arch? Assume you are 5 feet tall.
     ::你距离一个68英尺高的拱门站着100英尺。你必须从什么角度向上看拱门的顶部?假设你5英尺高。
  播放段落
  3. The angle of elevation of the top of a church to a point 100 feet away from the base is $\begin{array}{r}{60}^{\circ }\end{array}$ . Find the height of the church.
     ::教堂顶部高到距离基地100英尺的高度角是60英尺。 找到教堂的高度。

  播放段落

  You are standing and looking at a large painting on the wall. The bottom of the painting is 1 foot above your eye level. The painting is 10 feet tall. Assume you are standing $\begin{array}{r}x\end{array}$  feet from the painting, and that angle $\begin{array}{r}\theta \end{array}$ is formed by the lines of vision to the bottom and to the top of the painting.
  ::你正站在墙上看着一幅大画。画底部在你眼睛的高度上方一英尺。 画底有10英尺高。 假设你站在画底的一英尺外, 这个角由图底和画顶的视觉线形成 。

  播放段落
  4. Draw a picture to represent this situation.
     ::绘制图片来代表这种情况 。
  播放段落
  5. Solve for $\begin{array}{r}\theta \end{array}$ in terms of $\begin{array}{r}x\end{array}$ .
     ::以x为单位 解决 . . . . . . . .
  播放段落
  6. If you are standing 10 feet from the painting, what is $\begin{array}{r}\theta \end{array}$ ?
     ::如果你站在离画十尺远的地方, 什么是?
  播放段落
  7. If $\begin{array}{r}\theta ={30}^{\circ }\end{array}$ , how far are you standing from the wall (to the nearest foot)?
     ::如果"30",你站在墙上多远?

  播放段落
  8. A 50-foot-high tower is secured with a guy-wire anchored 8 feet from the base of the tower. What angle will the guy-wire make with the ground?
     ::50英尺高的塔楼有一条人电线 固定在离塔底8英尺的地方
  播放段落
  9. A 30-foot-tall flagpole casts a 12-foot shadow. What is the angle that the sun hits the flagpole?
     ::一只30英尺长的旗杆投下了12英尺长的阴影。 太阳击中旗杆的角度是什么?

  播放段落

  A water wheel with  a radius of 10 m is partially submerged  3 m  under water. The wheel makes one revolution in 360°, and the bucket starts at the center and initially moves upward. 
  ::半径为10米的水轮在水下被部分淹没3米。轮子在360度发生一次革命,桶子从中间开始,开始向上移动。

  播放段落
  10. Write a sine function to model the height of the bucket .
      ::写入一个正弦函数以模拟桶的高度。
  播放段落
  11. If $\begin{array}{r}x={40}^{\circ }\end{array}$ , determine the height of the bucket . 
      ::如果 x=40,确定桶的高度。

  播放段落

  Recall that if the latitude of the location is known, then the following formula can be used to calculate the angle of inclination of the sun on any given date of the year:
  ::回顾如果知道位置的纬度,可使用下列公式计算每年任何特定日期太阳倾角角:

  播放段落

  $\begin{array}{r}\text{Angle of sun}={90}^{\circ }-\text{latitude}+-{23.5}^{\circ }\cdot \cos \left[(N+10)\frac{360}{365}\right],\end{array}$ where $\begin{array}{r}N\end{array}$ represents the number of the day of the year that corresponds to the date of the year.
  ::太阳角=90latitude23.5cos[((N+10)360365),其中N表示年数与年数对应的年数。

  播放段落
  12. Determine the measurement of the sun’s angle of inclination for a building located at a latitude of $\begin{array}{r}{30}^{\circ }\end{array}$ , April $\begin{array}{r}12\end{array}$ , the $\begin{array}{r}102th\end{array}$ day of the year.
      ::确定位于年4月12日即每年第102天纬度30°Z的建筑物的太阳倾角的测量。
  播放段落
  13. Determine the measurement of the sun’s angle of inclination for a building located at a latitude of $\begin{array}{r}{50}^{\circ }\end{array}$ , August $\begin{array}{r}14\end{array}$ , the $\begin{array}{r}226th\end{array}$ day of the year.
      ::确定位于年8月14日第226天,即50°Z,8月14日的纬度的建筑物的太阳倾角。

  播放段落

  The alternating half-daily cycles of the rise and fall of the ocean are called tides. In one bay, the tides caused the water level to rise 6.5 m above and fall 6.5 m below the average sea level. The tide completes one cycle every 12 hours.
  ::海洋升降的半日交替周期被称为潮汐。 在一个海湾,潮汐导致水位上升6.5米以上,低于平均海平面下方6.5米。 潮汐每12小时完成一个周期。

  播放段落
  14. Write a sine function to model the height of the water with respect to average sea level.
      ::写入一个正弦函数,用平均海平面来模拟水的高度。
  播放段落
  15. If high tide is at 8 a.m., determine where the water level would be at 2:30 p.m. 
      ::如果高潮时间为上午8时,确定水位为下午2时30分。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。