课程： 8.4 总数和差异

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节合计和差异

折叠展开
合计和差异
Introduction
::导言

Sound waves and tones can be modeled by tuning forks. One sound might be modeled by the equation $\begin{aligned} s = 3 \sin 2 π t, \end{aligned}$ and another might be modeled by $\begin{aligned} s = 4 \sin (t + 3) . \end{aligned}$ It may be difficult to compare the tones without graphing. While trigonometric functions do not follow the properties of integers, they have identities that can be used to manipulate their variables.
::声波和音调调色调可以通过调制叉进行模拟。一种声音可以用方程式 s=3sin2t 进行模拟,另一种声音可能用 s=4sin( t+3) 进行模拟, 不绘制图形就很难比较音调。虽然三角度函数不跟随整数的属性, 它们具有可用于操纵变量的身份。

In mathematics, the difference between exact and approximate values is always an issue. At this point with trigonometry, the only trigonometric functions known exactly are summarized in the unit circle . However, knowledge of these functions provides enough information to find the of $\begin{aligned} 15^{\circ} \end{aligned}$ (the difference of $\begin{aligned} 45^{\circ} \end{aligned}$ and $\begin{aligned} 30^{\circ} \end{aligned}$ ) and $\begin{aligned} 75^{\circ} \end{aligned}$ ( the sum of $\begin{aligned} 45^{\circ} \end{aligned}$ and $\begin{aligned} 30^{\circ} \end{aligned}$ ) .
::在数学方面,精确值和近似值之间的差别总是个问题。在三角测量学方面,唯一确切知道的三角函数在单位圆中被总结。然而,对这些函数的了解提供了足够的信息,可以找到15个(45个和30个)和75个(45个和30个)和75个(45个和30个)。

Using the unit circle and a new set of identities, determine $\begin{aligned} \sin 15^{\circ} \end{aligned}$ and $\begin{aligned} \sin 75^{\circ} . \end{aligned}$
::使用单位圆和一套新的身份,确定sin15和sin75。

Sum and Difference Identities
::合计和差异

There are some intuitive but incorrect formulas for sums and differences with respect to trigonometric functions. For example, $\begin{aligned} \sin (θ + β) \neq \sin θ + \sin β \end{aligned}$ is one of the most common incorrect guesses as to the sum and difference identity .
::对于三角函数的数值和差异,有一些直观但不正确的公式。例如,sin 是对于总和和和差异特性最常见的不正确的猜测之一。

First, look at the derivation of the cosine difference identity:
::首先,看看余弦差异特性的衍生:

$\begin{aligned} \cos (α - β) = \cos α \cos β + \sin α \sin β \end{aligned}$

:)=coscossinsinsin

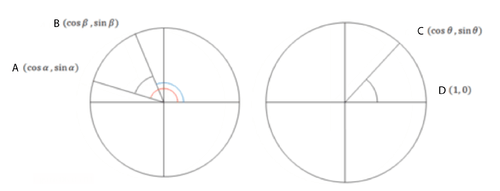
Start by drawing two arbitrary angles, $\begin{aligned} α \end{aligned}$ and $\begin{aligned} β \end{aligned}$ . In the image above, $\begin{aligned} α \end{aligned}$ is the angle in red and $\begin{aligned} β \end{aligned}$ is the angle in blue. The difference $\begin{aligned} α - β \end{aligned}$ is noted in black as $\begin{aligned} θ \end{aligned}$ . The reason why there are two pictures is because the image on the right has the same angle $\begin{aligned} θ \end{aligned}$ in a rotated position. This will be useful to work with because the length of $\begin{aligned} \bar{A B} \end{aligned}$ will be the same as the length of $\begin{aligned} \bar{C D} \end{aligned}$ .
::以绘制两个任意角度( α 和 ) 开始。在以上图像中, α 是红色角度, β 是蓝色角度。以黑色表示 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

T he length of $\begin{aligned} \bar{A B} \end{aligned}$ by using the distance formula:
::使用距离公式的 AB 长度 :

$\begin{aligned} \bar{A B} & = \sqrt{(\cos α - \cos β)^{2} + (\sin α - \sin β)^{2}} \end{aligned}$

::AB (coscos)2+(sinsin)2

The length of $\begin{aligned} \bar{C D} \end{aligned}$ by using the distance formula:
::使用距离公式的 CD 长度 :

$\begin{aligned} \bar{C D} = \sqrt{(\cos θ - 1)^{2} + (\sin θ - 0)^{2}} \end{aligned}$

::CD {( cos% 1) 2+( sin0) 2

Since $\begin{aligned} \bar{A B} = \bar{C D} \end{aligned}$ ,
::自从AB'C'D',

$\begin{aligned} \sqrt{(\cos α - \cos β)^{2} + (\sin α - \sin β)^{2}} & = \sqrt{(\cos θ - 1)^{2} + (\sin θ - 0)^{2}} \\ (\cos α - \cos β)^{2} + (\sin α - \sin β)^{2} & = (\cos θ - 1)^{2} + (\sin θ - 0)^{2} . \end{aligned}$

:coscos)2+(sinsin)2=(cos1)2+(sin0)(2(coscos)2+(sinsin)2=(cos1)2+(sin0))。

Multiply through the squared terms and simplify, using algebra.
::乘以平方条件,使用代数简化。

$\begin{aligned} (\cos α)^{2} - 2 \cos α \cos β + (\cos β)^{2} + (\sin α)^{2} - 2 \sin α \sin β + (\sin β)^{2} = (\cos θ)^{2} - 2 \cos θ + 1 + (\sin θ)^{2} \end{aligned}$

:cos)2-2-2cos(cos)2+(sin)2-2sin(sin)2=(cos)2-2-2cos1+(sin)2

Use the Pythagorean Trigonometric Identity to further simplify.
::使用毕达哥里安三角特征来进一步简化。

$\begin{aligned} 2 - 2 \cos α \cos β - 2 \sin α \sin β & = (\cos θ)^{2} - 2 \cos θ + 1 + (\sin θ)^{2} \\ 2 - 2 \cos α \cos β - 2 \sin α \sin β & = 1 - 2 \cos θ + 1 \\ - 2 \cos α \cos β - 2 \sin α \sin β & = - 2 \cos θ \\ \cos α \cos β + \sin α \sin β & = \cos θ \\ = \cos (α - β) \end{aligned}$

::2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -1 -1 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2

The proof for the sine and tangent functions are left as an example and in the exercises. Cotangent , secant, and cosecant are excluded because it is better to use .
::用于正切和相切函数的证明留作例子和练习。切除、割裂和割裂, 因为使用更好。 @ info: whatsthis

Difference Identities
::相异异度

$\begin{aligned} \cos (α - β) = \cos α \cos β + \sin α \sin β \end{aligned}$

:)=coscossinsinsin

$\begin{aligned} \sin (α - β) = \sin α \cos β - \cos α \sin β \end{aligned}$

:)=sincoscoscossinsin

$\begin{aligned} \tan (α - β) = \frac{\sin (α - β)}{\cos (α - β)} = \frac{\tan α - \tan β}{1 + \tan α \tan β} \end{aligned}$

::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

The sum identities are nearly the same as the difference identities. However, notice the change in signs in the sum identities.
::总和身份与差异身份几乎相同,但请注意总和身份的标志变化。

Sum Identities
::身份证明

$\begin{aligned} \cos (α + β) = \cos α \cos β - \sin α \sin β \end{aligned}$

:)=coscossinsinsin

$\begin{aligned} \sin (α + β) = \sin α \cos β + \cos α \sin β \end{aligned}$

:)=sincoscoscossinsin

$\begin{aligned} \tan (α + β) = \frac{\sin (α + β)}{\cos (α + β)} = \frac{\tan α + \tan β}{1 - \tan α \tan β} \end{aligned}$

::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

Examples using the for sine and tangent functions can be seen in the following videos:
::使用正弦和相切函数的例子可见于以下视频:





Examples
::实例

Example 1
::例1

Prove the sum identity for the cosine function .
::证明余弦函数的总和身份。

$\begin{aligned} \cos α \cos β - \sin α \sin β = \cos (α + β) \end{aligned}$

: )

Solution:
::解决方案 :

Step 1: Start with the cosine of a difference and make a substitution. Then use the odd-even identity.
::第1步:从差异的余弦开始进行替换。然后使用奇数身份。

$\begin{aligned} \cos α \cos β + \sin α \sin β = \cos (α - β) \end{aligned}$

: )

Step 2: Let $\begin{aligned} γ = - β \end{aligned}$
::第2步:让我们____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} \cos α \cos (- γ) + \sin α \sin (- γ) & = \cos (α + γ) \\ \cos α \cos γ - \sin α \sin γ & = \cos (α + γ) \end{aligned}$

::

Example 2
::例2

Find the exact value of $\begin{aligned} \tan 15^{\circ} \end{aligned}$ without using a calculator.
::在不使用计算器的情况下查找 tan% 15 的准确值。

Solution:
::解决方案 :

Step1:
::步骤1:

$\begin{aligned} \tan 15^{\circ} = \tan (45^{\circ} - 30^{\circ}) \\ = \frac{\tan 45^{\circ} - \tan 30^{\circ}}{1 + \tan 45^{\circ} \tan 30^{\circ}} \\ = \frac{1 - \frac{\sqrt{3}}{3}}{1 + 1 \cdot \frac{\sqrt{3}}{3}} \\ = \frac{3 - \sqrt{3}}{3 + \sqrt{3}} \end{aligned}$

::~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Step 2: A final solution is rationalized . In this case, multiplying through by the conjugate of the denominator will eliminate the radical.
::步骤2:最终解决方案的合理化。在这种情况下,乘以分母的组合,将消除激进主义。

$\begin{aligned} = \frac{(3 - \sqrt{3}) \cdot (3 - \sqrt{3})}{(3 + \sqrt{3}) \cdot (3 - \sqrt{3})} \\ = \frac{9 - 6 \sqrt{3} + 3}{9 - 3} \\ = \frac{12 - 6 \sqrt{3}}{6} \\ = 2 - \sqrt{3} \end{aligned}$

Example 3
::例3

Evaluate the expression exactly without using a calculator.
::准确评价表达式而不使用计算器。

$\begin{aligned} \cos 50^{\circ} \cdot \cos 5^{\circ} + \sin 50^{\circ} \cdot \sin 5^{\circ} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么?

Solution:
::解决方案 :

Apply c osine of a difference.
::应用差异的余弦。

$\begin{aligned} \cos 50^{\circ} \cos 5^{\circ} + \sin 50^{\circ} \sin 5^{\circ} & = \cos (50^{\circ} - 5^{\circ}) \\ = \cos 45^{\circ} \\ = \frac{\sqrt{2}}{2} \end{aligned}$

::====================================================================================================================================== ================================================================================================================================

Example 4
::例4

Return to the problem in the Introduction, u sing the unit circle and a new set of identities to determine $\begin{aligned} \sin 15^{\circ} \end{aligned}$ and $\begin{aligned} \sin 75^{\circ} \end{aligned}$ .
::回到导言中的问题,利用单位圈和一套新的身份来确定sin15和sin75。

Solution:
::解决方案 :

In order to evaluate $\begin{aligned} \sin 15^{\circ} \end{aligned}$ and $\begin{aligned} \sin 75^{\circ} \end{aligned}$ exactly without a calculator, use the sine of a difference and the sine of a sum.
$\begin{aligned} \sin (45^{\circ} - 30^{\circ}) & = \sin 45^{\circ} \cos 30^{\circ} - \cos 45^{\circ} \sin 30^{\circ} \\ = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \cdot \frac{1}{2} \\ = \frac{\sqrt{6} - \sqrt{2}}{4} \\ \sin (45^{\circ} + 30^{\circ}) & = \sin 45^{\circ} \cos 30^{\circ} + \cos 45^{\circ} \sin 30^{\circ} \\ = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} \\ = \frac{\sqrt{6} + \sqrt{2}}{4} \end{aligned}$

::为了评估 sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Example 5
::例5

Prove the sine of a difference identity.
::证明差异认同的必要条件。

$\begin{aligned} \sin (α - β) = \sin α \cos β - \cos α \sin β \end{aligned}$

:)=sincoscoscossinsin

Solution:
::解决方案 :

Start with the cofunction identity , and then distribute and work out the cosine of a sum and cofunction identities.
::以共用身份开始, 然后分配和解决余弦和共用身份。

$\begin{aligned} \sin (α - β) & = \cos (\frac{π}{2} - (α - β)) \\ = \cos ((\frac{π}{2} - α) + β) \\ = \cos (\frac{π}{2} - α) \cos β - \sin (\frac{π}{2} - α) \sin β \\ = \sin α \cos β - \cos α \sin β \end{aligned}$

:) =cos() =cos() () () () () () () () () () () () () () () () () () () () () () () () () () () () () ) () () () () () () () () () () () () () () () () () ) (() () () (() () () () () (() ) ) () (() ) (() ) () ((() ) ) (() () ) ) ) () () ) ) ((() ) )

Example 6
::例6

Use a sum or difference identity to find an exact value of $\begin{aligned} \cot (\frac{5 π}{12}) \end{aligned}$ .
::使用一个总和或差异身份来查找 cot( 512) 的准确值。

Solution :
::解决方案 :

Start with the definition of cotangent as the inverse of tangent.
::以正切值定义为反正切值开始。

$\begin{aligned} \begin{aligned} \cot (\frac{5 π}{12}) & = \frac{1}{\tan (\frac{5 π}{12})} \\ = \frac{1}{\tan (\frac{9 π}{12} - \frac{4 π}{12})} \\ = \frac{1}{\tan (\frac{3 π}{4} - \frac{π}{3})} \\ = \frac{1 + \tan \frac{3 π}{4} \cdot \tan \frac{π}{3}}{\tan \frac{3 π}{4} - \tan \frac{π}{3}} \\ = \frac{1 + (- 1) \cdot \sqrt{3}}{(- 1) - \sqrt{3}} \\ = \frac{1 - \sqrt{3}}{- 1 - \sqrt{3}} \cdot \frac{- 1 + \sqrt{3}}{- 1 + \sqrt{3}} \\ = \frac{- 1 + 2 \sqrt{3} - 3}{1 - 3} \\ = \frac{- 4 + 2 \sqrt{3}}{- 2} \\ = 2 - \sqrt{3} \end{aligned} \end{aligned}$

:5)12=1tan(512)=1tan(912-412)=1tan(343) =1+tan(344333334 - tan3=1+(11)3=1+(13)3=1-1-1-3-1-3__1+3-1+3+31+23-31-3__4+23-2=2-3)

Example 7
::例7

Prove the following identity: $\begin{aligned} \frac{\sin (x - y)}{\sin (x + y)} = \frac{\tan x - \tan y}{\tan x + \tan y} . \end{aligned}$
::证明以下身份:sin(x-y)sin(x+y)=tanx-tanytanx+tany。

Solution:
::解决方案 :

$\begin{aligned} \begin{aligned} \frac{\sin (x - y)}{\sin (x + y)} & = \frac{\sin x \cos y - \cos x \sin y}{\sin x \cos y + \cos x \sin y} \\ = \frac{\sin x \cos y - \cos x \sin y}{\sin x \cos y + \cos x \sin y} \cdot \frac{(\frac{1}{\cos x \cdot \cos y})}{(\frac{1}{\cos x \cdot \cos y})} \\ = \frac{(\frac{\sin x \cos y}{\cos x \cdot \cos y}) - (\frac{\cos x \sin y}{\cos x \cdot \cos y})}{(\frac{\sin x \cos y}{\cos x \cdot \cos y}) + (\frac{\cos x \sin y}{\cos x \cdot \cos y})} \\ = \frac{\tan x - \tan y}{\tan x + \tan y} \end{aligned} \end{aligned}$

:x+Y) = (sin) xxxxxxxxxxxxxxxxxxxxxxxxxin}}}{Y}}(x+Y) = (sinxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}}}) = (cusxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxn_}}}{}}}

Summary
::摘要

Difference Identities
::相异异度

$\begin{aligned} \cos (α - β) = \cos α \cos β + \sin α \sin β \\ \sin (α - β) = \sin α \cos β - \cos α \sin β \\ \tan (α - β) = \frac{\sin (α - β)}{\cos (α - β)} = \frac{\tan α - \tan β}{1 + \tan α \tan β} \end{aligned}$

::

Sum Identities
::身份证明

$\begin{aligned} \cos (α + β) = \cos α \cos β - \sin α \sin β \\ \sin (α + β) = \sin α \cos β + \cos α \sin β \\ \tan (α + β) = \frac{\sin (α + β)}{\cos (α + β)} = \frac{\tan α + \tan β}{1 - \tan α \tan β} \end{aligned}$

:) () () () () () () () () () () () () () () () () () 1-() () () () () () () () ()

Review
::回顾

Find the exact value for each expression by using a sum or difference identity:
::使用总和或差异特性查找每个表达式的准确值 :

1. $\begin{aligned} \cos 75^{\circ} \end{aligned}$
::1. 承担第75-75-______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2. $\begin{aligned} \cos 105^{\circ} \end{aligned}$
::2. COS105_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3. $\begin{aligned} \cos 165^{\circ} \end{aligned}$
::3,cos165

4. $\begin{aligned} \sin 105^{\circ} \end{aligned}$
::4 sin 105______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

5. $\begin{aligned} \sec 105^{\circ} \end{aligned}$
::5 秒 105

6. $\begin{aligned} \tan 75^{\circ} \end{aligned}$
::6. 锡 75_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

7. Prove the sine of a sum identity.
::7. 证明真实身份的必要条件。

8. Prove the tangent of a sum identity.
::8. 证明一个总特征的相切性。

9. Prove the tangent of a difference identity.
::9. 证明差异认同的相切性。

10. Evaluate without a calculator: $\begin{aligned} \cos 50^{\circ} \cos 10^{\circ} - \sin 50^{\circ} \sin 10^{\circ} \end{aligned}$ .
::10. 无计算器的评价:cos50cos10sin50sin10。

11. Evaluate without a calculator: $\begin{aligned} \sin 35^{\circ} \cos 5^{\circ} - \cos 35^{\circ} \sin 5^{\circ} \end{aligned}$ .
::11. 评估没有计算器:sin_35cos_5cos_35sin_55。

12. Evaluate without a calculator: $\begin{aligned} \sin 55^{\circ} \cos 5^{\circ} + \cos 55^{\circ} \sin 5^{\circ} \end{aligned}$ .
::12. 评估没有计算法:sin55cos55cos55sin555。

13. If $\begin{aligned} \cos α \cos β = \sin α \sin β \end{aligned}$ , then what does $\begin{aligned} \cos (α + β) \end{aligned}$ equal?
::13. 如果cosççosísinsin,那么cos()等于什么?

14. Prove that $\begin{aligned} \tan (x + \frac{π}{4}) = \frac{1 + \tan x}{1 - \tan x} \end{aligned}$ .
::14. 证明Tan(x4)=1+tanx1-tanx。

15. Prove that $\begin{aligned} \sin (x + π) = - \sin x . \end{aligned}$
::15. 证明这一罪行。

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

章节大纲

常规

合计和差异

Introduction ::导言

Sum and Difference Identities ::合计和差异

Difference Identities ::相 异 异 度

Sum Identities ::身份证明

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Sum and Difference Identities
::合计和差异

Difference Identities
::相异异度

Sum Identities
::身份证明

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)