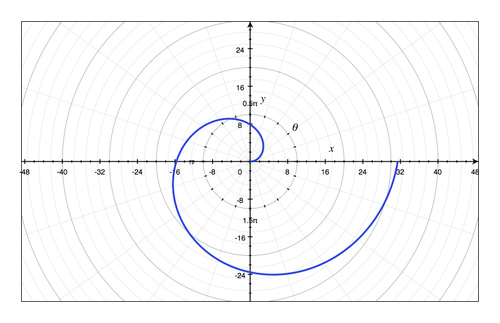
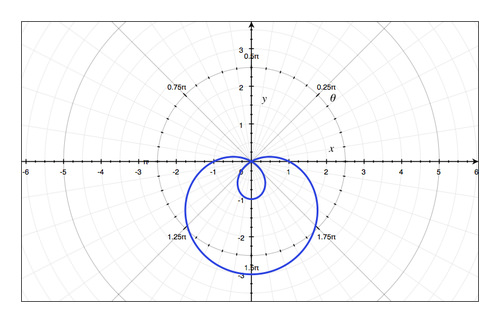
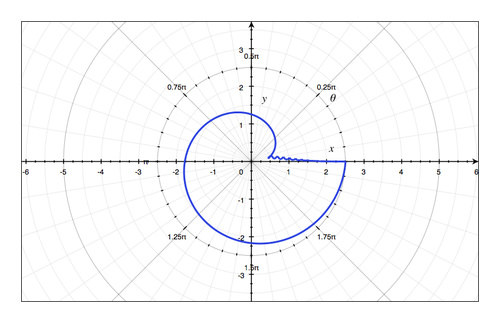
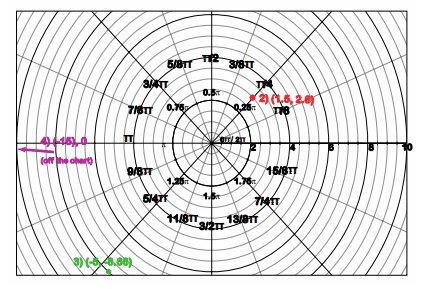
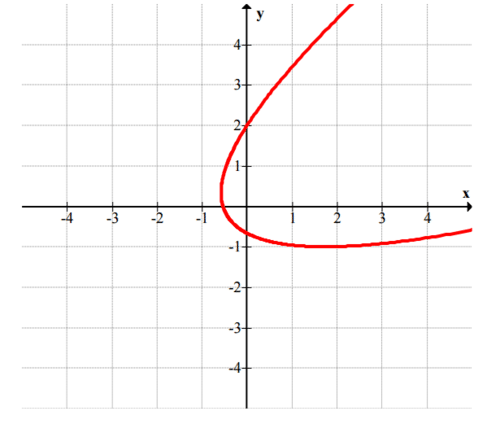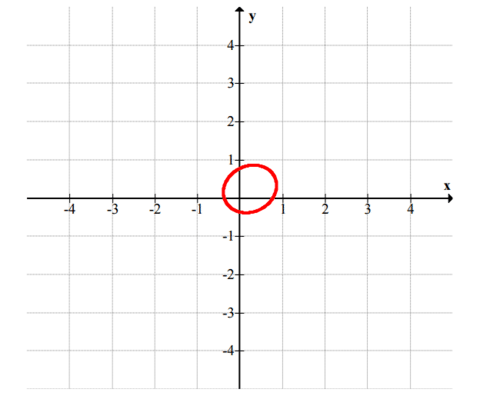16.12 答复 -- -- 第12章:极地坐标和参数等同
章节大纲
-
Section 12.2: Polar Coordinate System
::第12.2节:极地坐标系统-
Because a given point may have multiple descriptions
::因为给定点可能有多个描述 -
If
r
<
0
, you extend to the left to measure the distance. If
θ
>
360
, you circle around and continue.
::如果 r < 0, 则向左延伸以测量距离。 如果 + 360, 则围绕并继续 。 -
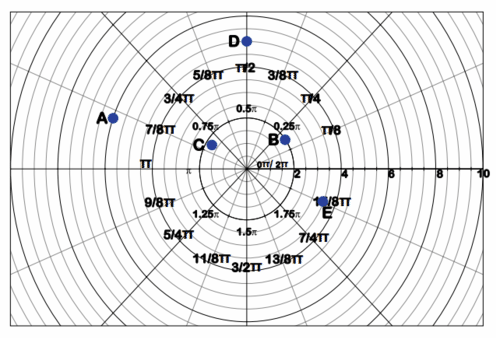
See point A below.
::见下文A点。 -
See point B above.
::见上文B点。 -
See point C above.
::见上文C点。 -
See point D above.
::见上文D点。 -
See point E above.
::见上文E点。 -
(-1.5, -190°) and (1.5, 0.945π)
:-1.5,-190°)和(1.5, 0.9450°)
-
(
5
,
5
π
3
)
and
(
-
5
,
-
60
∘
)
:5,53)和(5,60)
-
(
-
3
,
-
55
)
and
(
3
,
1.7
π
)
:3-3-55)和(3,1,7)
-
(4, -150°) and (-4,
5
π
6
)
:4,-150°)和(4,5°6)
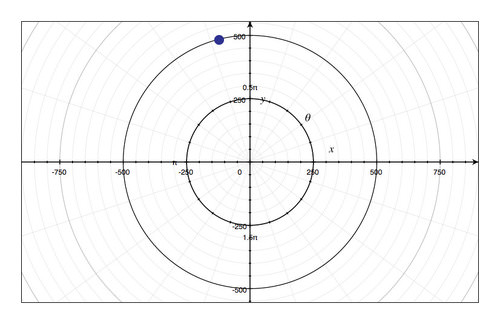
- (500, 105°)
-
-
a.
4.189
x
10
7
b. 3.837 x 10 7
c. 3.004 x 10 7
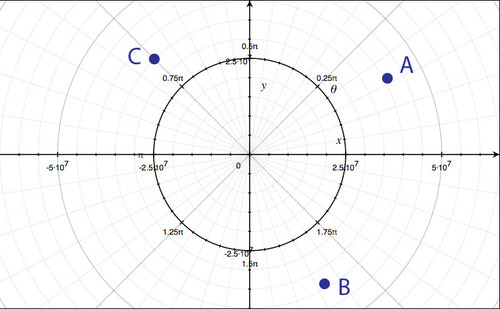
::a. 4.189 x 107 b. 3.837 x 107 c. 3.004 x 107 -
a.
(
4.189
x
10
7
,
30
∘
)
b. ( 3.837 x 10 7 , - 60 ∘ )
c. ( 3.004 x 10 7 , 135 ∘ )
::a. (4.189x107,30)b.(3.837x107,-60)c.(3.004x107,135) -
Section 12.3: Polar Equations
::第12.3节:极赤道Section 12.4: Polar and Cartesian Transformation
::第12.4节:极地和笛卡尔转变- (-5, 0)
-
(1.5, 2.6) Point plotted below.
:1.5、2.6) 点图如下。
-
(-5, -8.66) Point plotted above.
:5至8.66)以上点图。
-
(-15, 0) Point noted above.
:15,0)上述点。
-
(
√
50
,
-
π
4
)
or (7.07, -0.79)
( √ 50 , 7 π 4 ) or (7.07, 5.50)
::或(7.07,-0.79)或(7.07,5.50)或(7.07,5.50) -
(
10
,
π
2
)
or (10, 1.57)
( 10 , - 3 π 2 ) or (10, -4.71)
:10,%2)或(10,1.57) (10,3,%2)或(10,4.71)
-
(10, 2.50)
(10, -3.79) -
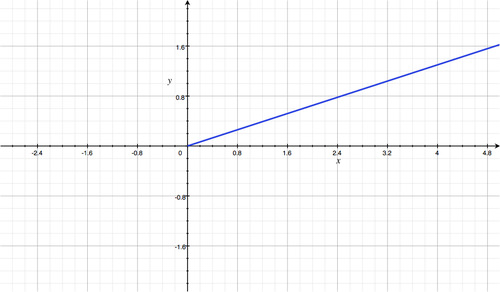
Approximate equation is
y
=
.33
x
.
This is a line with domain
x
≥
0
. It starts at the origin and has a slope of about 0.325.
::近似方程式为 Y= 33x。 这是域的直线 x_0。 它从原点开始, 斜度约为 0. 325 。 -
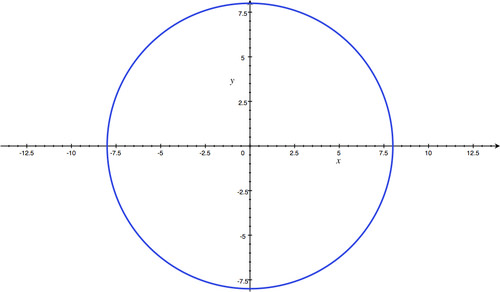
x
2
+
y
2
=
64.
This is a circle centered at the origin with radius 8.
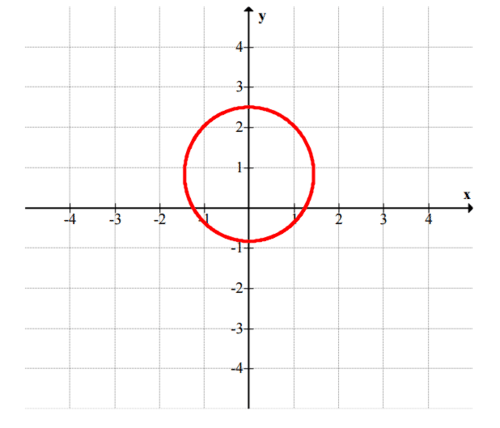
::x2+y2=64。 这是一个圆, 以原点为中心, 半径为 8 。 -
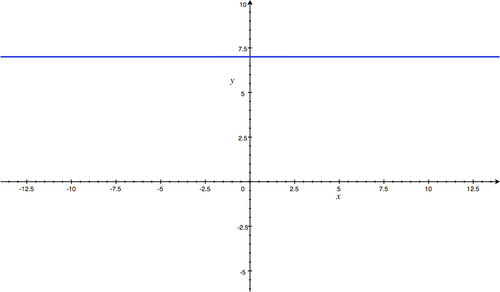
y
=
7.
This is a horizontal line through (0, 7).
::y=7. 这是一条通过 0, 7 的水平线 。 -
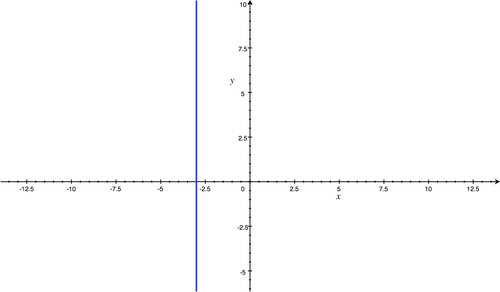
x
=
-
3.
This is a vertical line through (-3, 0).
::x=-3. 这是一条直径( 3, 0) 的垂直线 。 -
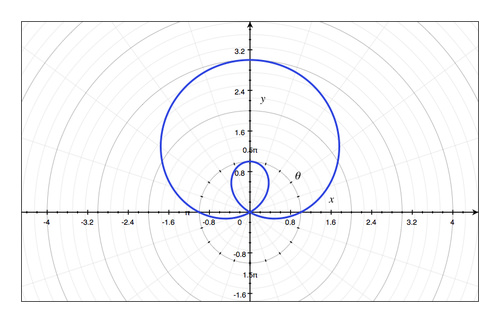
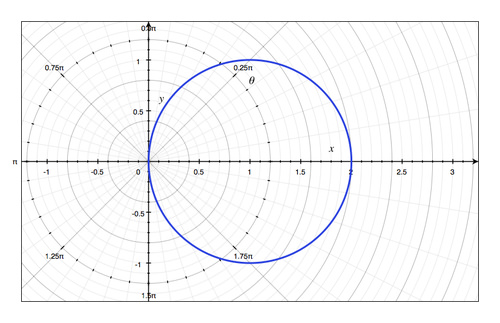
r
=
2
cos
θ
.
This is a circle with center at (1, 0) and radius 1.
::r=2cos。 这是一个圆形, 中心在 1, 0 和 半径 1 。 -
sin
θ
=
√
3
cos
θ
.
This is a line with slope equal to the square root of 3.
::这是一条斜坡等于3平方根的直线。 -
r
sin
θ
=
-
5.
This is a horizontal line through (0, -5).
::rsin% - 5。 这是一条通过 0, - 5 的水平线 。 -
r
cos
θ
×
r
sin
θ
=
15
or
r
2
cos
θ
sin
θ
=
15.
This is a rational function centered at the origin.
::rcos × rsin 15 或 r2cossin 15。 这是一个以源代码为中心的合理函数 。 -
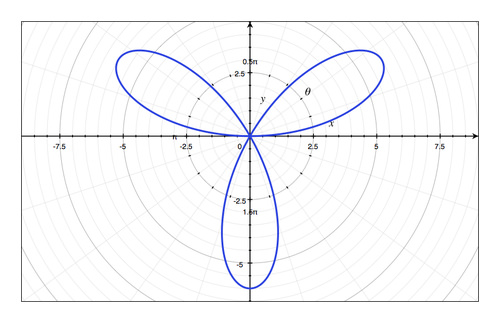
√
4
,
380
π
=
132
cos
(
5
θ
)
::4,380132cos(5__) -
l
=
√
7
,
542
π
cos
5
θ
::7,542cos5 -
y
=
6
17
−
x
cos
25
∘
sin
25
∘
or
y
≈
-
2.14
x
+
0.835
::y=617-xcos25sin25或y-2.14x+0.835
Section 12.5: Systems of Polar Equations
::第12.5节:极赤道系统-
They intersect twice.
::它们交叉了两次 -
Once in the 1st and once in the 4th quadrant
::一次在第一 一次在第四象限 -
They intersect at
(
1
,
π
3
)
and
(
1
,
5
π
3
)
.
::相交于(1,3,3)和(1,5,3)之间。 -
3 points of intersection
::3个交叉点 -
Points of intersection are
(
0
,
0
)
,
(
1
2
,
π
2
)
,
and
(
1
2
,
5
π
3
)
.
::交叉点是(0,0,(12,)2)和(12,513)。 - ( 2 , 0 )
- ( 0 , 0 )
-
(
2
+
√
2
,
3
π
4
)
and
(
2
−
√
2
,
7
π
4
)
:2,34)和(2,2,74)
- ( 3 2 , π 3 ) , ( 3 2 , 5 π 3 )
-
(
√
2
,
π
4
)
,
(
√
2
,
3
π
4
)
-
(
0
,
0
)
,
(
1
,
0
)
-
(
0
,
0
)
,
(
√
3
2
,
2
π
3
)
,
(
√
3
2
,
π
3
)
-
(
0
,
0
)
,
(
2
√
2
,
5
π
4
)
-
(1, 276°), (2.44, 313°)
-
(0, 0), (1.08, 95°), (1,77, 142°), (1.77, 218°), (1.08, 265°)
Section 12.6: Polar Equations of Conics
::第12.6节:二次曲线极赤道-
8
x
2
−
10
x
+
9
y
2
−
25
=
0
;
ellipse
::8x2- 10x+9y2- 25=0; 椭圆 -
3
x
2
−
8
x
+
4
y
2
−
16
=
0
;
ellipse
::3x2-8x+4y2 - 16=0; 椭圆 -
3
x
2
−
4
x
+
4
y
2
−
4
=
0
;
ellipse
::3x2 - 4x+4y2 - 4=0; 椭圆 -
−
12
x
2
−
24
x
+
4
y
2
−
9
=
0
;
hyperbola
::- 12x2 - 24x+4y2 - 9=0;双波 -
x
2
−
5
x
+
y
2
=
0
;
circle
::x2 - 5x+y2=0; 圆 -
-
-
-
-
-
::r=32-cos____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ -
::r=10cos24sin -
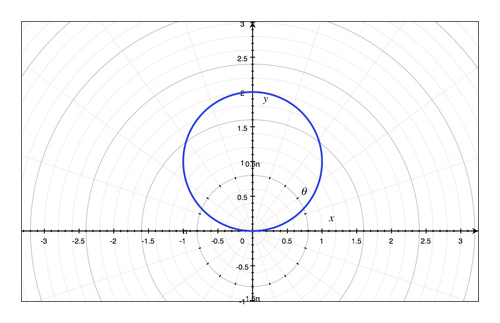
r
=
-
2
sin
θ
::r=-2sin -
r
=
2
cos
θ
::r=2cos -
r
=
1
1
−
2
cos
θ
::r=11-2cos_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ -
e
=
1
, parabola
::e=1, 抛物线 -
e
=
1
2
,
ellipse
::e=12, 椭圆 -
e
=
1
, parabola
::e=1, 抛物线 -
e
=
2
, hyperbola
::e=2,双波 -
Answers will vary. One example: On the rectangular grid, you graph points based on
x
and
y
values (how far something is right/left or above/below the origin). On the polar grid, you graph points based on angles and the length of a radius.
::答案会有所不同。例如:在矩形网格中,根据 x 和 y 值(东西的右/ 左或上/ 上/ 下) 绘制的图形点。在极地网格中,根据角度和半径长度绘制的图形点。
Section 12.7: Polar Form of Complex Numbers
::第12.7节:复杂数字的极表形式-
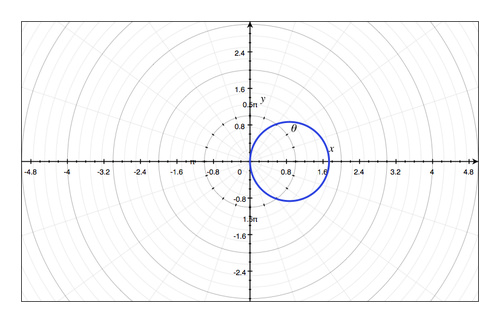
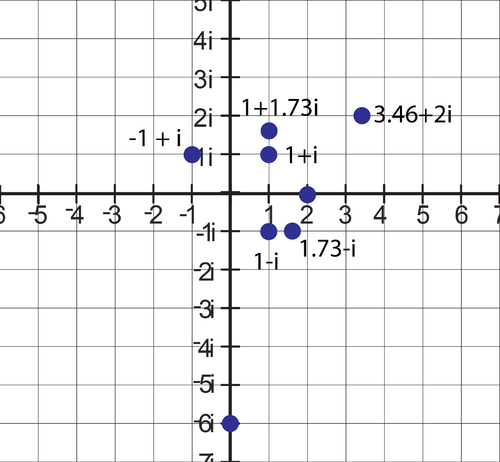
See graph above.
(
√
2
,
45
∘
)
::见上文图表。 (第2,45__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ -
See graph above.
(
√
2
,
135
∘
)
::见上文图表。 (第2,135__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ -
See graph above.
(
6
,
270
∘
)
::见上文图表(6,270) -
::见上文图表。 (第2,45__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ -
::见上文图。 (%2,-45_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ -
::见上文图表(2,0) -
::见上文图表(2,60) -
::见上文图表(2,30) -
::见上文图表(4,30) -
4.25
+
4.25
i
::4.25+4.25i -
-
7.5
+
13
i
::-7.5+13i -
6
+
10.4
i
::6+10.4i 6+10.4i -
(
√
x
2
+
y
2
,
1
s
i
n
(
y
2
r
2
)
)
( cos θ + i sin θ ) using θ from above
:x2+y2,1sin(y2r2))(cosisin) 使用上面的
-
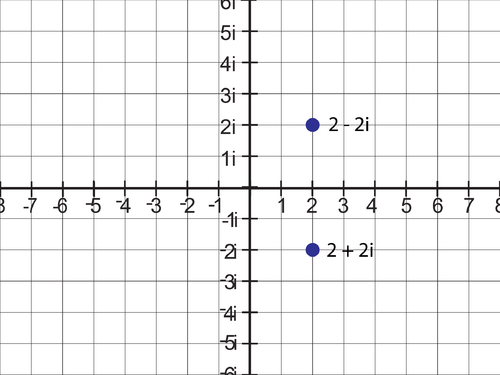
Zeros: 2 + 2i, 2 – 2i
::零:2+2i,2-2i - (0, 0°)
- ( √ 3 − 1 2 , 0 ∘ )
- ( √ 13 , 213.69 ∘ )
- (4, -30°)
Section 12.8: Product and Quotient Theorems
::第12.8节:产品和引号理论-
4
√
2
(
cos
15
∘
+
i
sin
15
∘
)
::42(cos15isin15) -
8
c
i
s
(
60
°)
::8cis( 60°) -
1
3
c
i
s
(
-
120
∘
)
::13CIS(-120) - 60°
-
33.81
+
9.06
i
::33.81+9.06i -
.36
+
1.35
i
::36+1.35i - 3 16
-
0
+
40
i
::0+40i -
1.4
+
4
5
i
::1.4+45i -
1
2
+
5
16
i
::12+516i -
-
32
+
32
i
√
3
::-32+32i%3 -
0
+
125
i
::0+125i -
2
√
3
+
2
+
(
2
√
3
−
2
)
i
::3+2+2+(2+3-2)i -
4
+
4
√
3
i
::4+43i -
3
+
2.6
i
::3+2.6i 3+2.6i -
-
1
6
−
2
7
i
::-16-27i -
-
23
40
−
27
56
i
::-2340-22756i - ( 32 7 , 30 ∘ )
- ( 84 , 37 ∘ )
Section 12.9: Powers and Roots of Complex Numbers
::第12.9节:复杂数字的权力和根源-
-
1
2
+
5
2
i
::-12+52i -
37
-
(
1
2
−
i
√
3
2
)
:12-i32)
-
4
√
2
(
cos
15
∘
+
i
sin
15
∘
)
::42(cos15isin15) -
8
c
i
s
(
60
∘
)
::8CIS( 60) -
4
c
i
s
(
9
π
40
)
::4Cisc(940) -
1
3
c
i
s
(
-
120
∘
)
::13CIS(-120) -
3
4
c
i
s
(
-
140
∘
)
::34Cis(-140) -
-
27
2
−
27
√
3
2
i
::- 272-2732i -
-
2
√
2
−
2
√
2
i
::-2-2-22i -
-
64
-
(
6
√
2
)
c
i
s
15
°,
6
√
2
c
i
s
135
°,
6
√
2
c
i
s
255
°
:6_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
-
2
c
i
s
67.5
°,
2
c
i
s
157.5
°,
2
c
i
s
247.5
°,
2
c
i
s
337.5
°
::2C67.5°, 2C157.5°, 2C247.5°, 2C337.5° -
c
i
s
18
°,
c
i
s
90
°,
c
i
s
162
°,
c
i
s
234
°,
c
i
s
306
°
::cis18°, cis90°, cis162°, cis234°, cis306°
Section 12.10: Parameters and Parameter Elimination
::第12.10节:参数和参数去除-
y
=
4
9
x
2
+
2
9
x
−
2
9
::y=49x2+29x-29 -
x
=
3
4
y
2
+
9
2
y
+
15
4
::x=34y2+92y+154 -
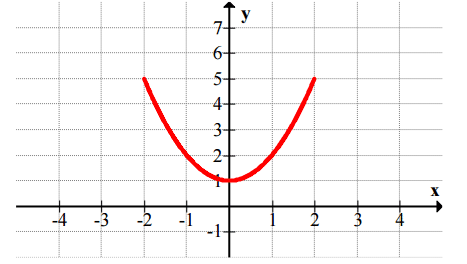
y
=
x
2
::y=x2 y=x2 -
y
=
x
3
+
15
x
2
+
75
x
+
126
::y=x3+15x2+75x+126 -
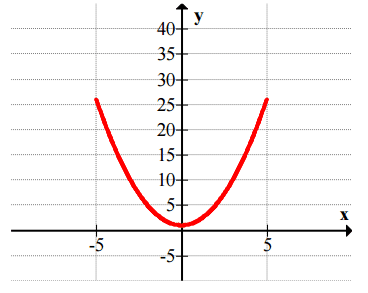
y
=
x
2
−
8
x
+
11
::y=x2 - 8x+11 y=x2 - 8x+11 -
-
-
-
-
-
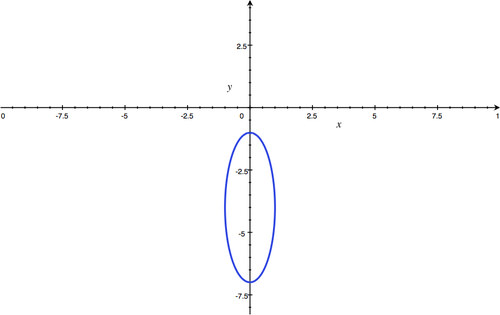
x
2
+
(
y
+
4
3
)
2
=
1
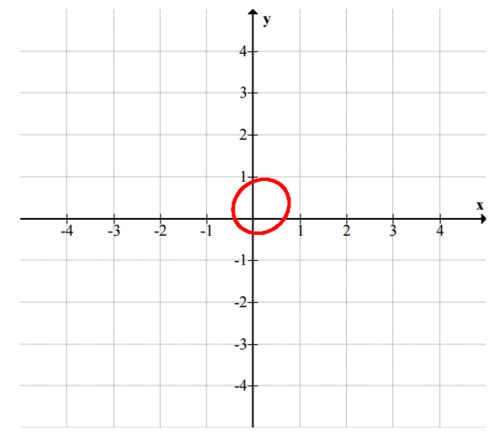
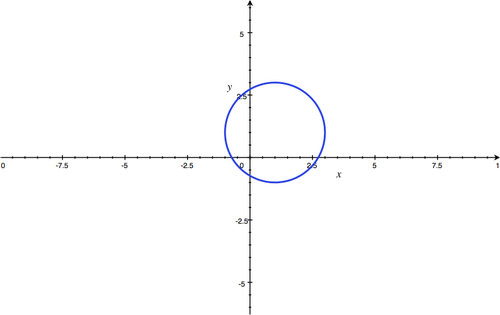
::x2+(y+43)2=1 -
(
x
−
1
)
2
+
(
y
−
1
)
2
=
4
:x-1)2+(y-1)2=4
-
x
=
2
+
3
cos
t
;
y
=
4
+
3
sin
t
::x=2+3cost;y=4+3sint -
x
=
2
cos
t
;
y
=
5
sin
t
::x=2 成本; y=5sint -
x
=
3
cos
t
+
4
;
y
=
6
sin
t
−
1
::x=3cost+4;y=6sint-1
Section 12.11: Parametric Inverses
::第12.11节:参数反数-
x
=
t
2
+
2
;
y
=
t
−
4
::x=t2+2; y=t- 4 -
Function
::函数职能职能职能职能职能职能职能职能 -
Neither
::中 无 -
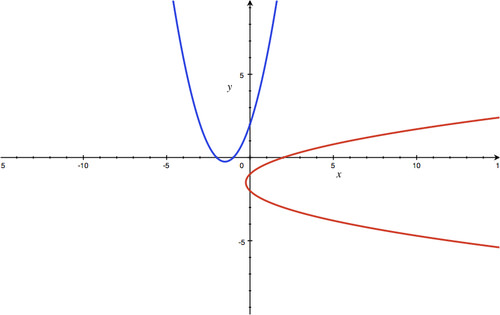
x
=
4
−
t
;
y
=
t
2
::x=4 - t; y=t2 x=4 - t; y=t2 -
Inverse
::反逆 -
Relation
::关系关系 -
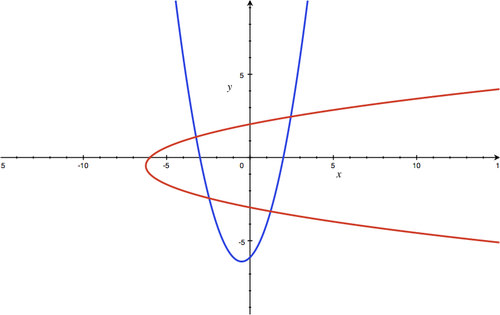
x
=
t
2
−
3
;
y
=
2
t
−
1
::x=t2 - 3; y=2t - 1 -
Inverse
::反逆 -
Function
::函数职能职能职能职能职能职能职能职能 -
x
=
t
2
−
2
t
;
y
=
3
t
+
14
::x=t2- 2t; y=3t+14 -
When
t
=
-
2
at
(
8
,
8
)
and when
t
=
7
at
(
35
,
35
)
::当 t = 2 时( 8, 8) , 当 t = 7 时( 35, 35) -
x
=
4
t
−
4
;
y
=
t
2
::x=4t- 4; y=t2 -
When
t
=
2
at
(
4
,
4
)
::当 t=2 时( 4, 4) -
x
=
t
;
y
=
t
2
+
t
−
6
::x=t; y=t2+t- 6 x=t; y=t2+t- 6 -
x
=
t
;
y
=
t
2
+
3
t
+
2
::x=t; y=t2+3t+2
Section 12.12: Applications of Parametric Equations
::第12.12节:参数等量的应用-
x
=
-
50
sin
2
π
5
t
;
y
=
-
50
cos
(
2
π
5
t
)
+
53
::x=- 50sin2°5t; y=- 50cos(2°5t)+53 - ( - 29.4 , 93.1 )
- ( 47.55 , 37.55 )
-
x
=
-
40
sin
(
π
3
(
t
+
1
)
)
;
y
=
-
40
cos
(
π
3
(
t
+
1
)
)
+
43
::x=- 40sin( 3( t+1); y=- 40cos( 3 ( t+1))+43 - ( 0 , 83 )
- ( 34.6 , 23 )
-
x
=
t
⋅
73.33
⋅
cos
π
4
;
y
=
1
2
⋅
(
-
32
)
⋅
t
2
+
t
⋅
73.33
⋅
sin
(
π
4
)
+
5
::x=t73.33cos4;y=12(- 32)\t2+t73.33sin(- 4)+5 - ( 103.7 , 44.7 )
-
172.7
feet in about
3.33
seconds
::大约3.33秒内172.7英尺 -
x
=
t
⋅
102.67
⋅
cos
(
π
3
)
+
8.8
t
;
y
=
1
2
⋅
(
-
32
)
⋅
t
2
+
t
⋅
102.67
⋅
sin
(
π
3
)
+
7
::x=t102.67cos(3)+8.8t;y=12(-32)t2+t102.67sin(3)+7 - ( 120.27 , 120.83 )
-
338.56
feet in about
5.63
seconds
::338.56英尺,约5.63秒 -
x
1
=
-
t
⋅
105.6
⋅
cos
(
π
3
)
+
250
+
8.8
t
;
y
1
=
1
2
⋅
(
-
32
)
⋅
t
2
+
t
⋅
105.6
⋅
sin
(
π
3
)
::x1 = - t105.6.6cos3+250+8. 8t; y1 = 12( 32) t2+t105. 6.6sin
3)
-
x
2
=
t
⋅
95.33
⋅
cos
(
π
4
)
+
8.8
t
;
y
2
=
1
2
⋅
(
-
32
)
⋅
t
2
+
t
⋅
95.33
⋅
sin
(
π
4
)
::x2 = t95.33cos( 4) + 8.8t; y2 = 12( 32) t2+ t95.33sin( 4) -
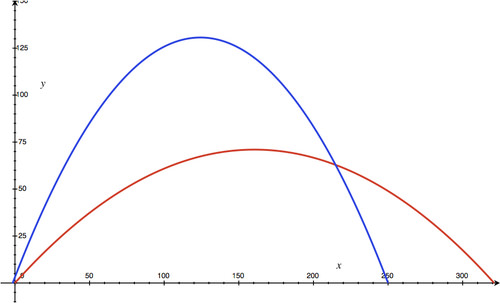
While the graphs intersect, each ball passes through the point of intersection at a different time.
::当图形交叉时,每个球会在不同的时间穿过交叉点。
-
Because a given point may have multiple descriptions