课程： 16.13 答复 -- -- 第13章:顺序和系列

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

答复----第13章:序列和系列

Section 13.2: Recursion
::第13.2节第13.2节:再货

$\begin{aligned} a_{1} = 3; a_{k} = a_{k - 1} + 4 \end{aligned}$
::a1=3;ak=ak -1+4

$\begin{aligned} a_{1} = 3; a_{k} = 3 a_{k - 1} \end{aligned}$
::a1=3;ak=3ak-1

$\begin{aligned} a_{1} = 3; a_{k} = a_{k - 1} + 3 \end{aligned}$
::a1=3;ak=ak -1+3

$\begin{aligned} a_{1} = 3; a_{k} = 2 a_{k - 1} \end{aligned}$
::a1=3;ak=2ak-1

$\begin{aligned} a_{1} = 1; a_{k} = 4 a_{k - 1} \end{aligned}$
::a1=1;ak=4ak-1
2, 8, 40, 208, 1,088, 5,696
4, 18, 56, 202, 684, 2,378
2, 5, 7, 12, 19, 31, 50, 81, 131, 212
550

$\begin{aligned} a_{1} = 1; a_{k} = 3 a_{k - 1} + 1 \end{aligned}$
::a1=1;ak=3ak-1+1

$\begin{aligned} a_{1} = 1; a_{k} = 3 a_{k - 1} + 2 \end{aligned}$
::a1=1;ak=3ak-1+2

$\begin{aligned} a_{1} = 2; a_{k} = 5 a_{k - 1} + 1 \end{aligned}$
::a1=2;ak=5ak-1+1

$\begin{aligned} a_{1} = 2; a_{2} = 3; a_{k} = a_{k - 1} \cdot a_{k - 2} \end{aligned}$
::a1=2; a2=3; ak=ak- 1ak-2

$\begin{aligned} a_{1} = 4; a_{2} = 6; a_{k} = a_{k - 1} + a_{k - 2} + 1 \end{aligned}$
::a1=4; a2=6; ak=ak- 1+ak-2+1

$\begin{aligned} a_{1} = 7; a_{2} = 13; a_{k} = 2 (a_{k - 1} + a_{k - 2}) \end{aligned}$
::a1=7; a2=13; ak=2( ak-1+ak-2)

Section 13.3: Arithmetic and Geometric Sequences
::第13.3节:测量和几何序列

17, 21, 25

$\begin{aligned} a_{k} = 1 + (k - 1) \cdot 4 \end{aligned}$
::ak=1+(k- 1)4
597
$\begin{aligned} \frac{4}{27}, \frac{4}{81}, \frac{4}{243} \end{aligned}$

$\begin{aligned} a_{k} = 12 \cdot {(\frac{1}{3})}^{k - 1} \end{aligned}$
::ak=12(13)k- 1

$\begin{aligned} \frac{12}{3^{16}} or \frac{4}{3^{15}} \end{aligned}$
::12316或4315
$\begin{aligned} \frac{2}{125}, - \frac{2}{625}, \frac{2}{3, 125} \end{aligned}$

$\begin{aligned} a_{k} = 10 \cdot {(- \frac{1}{5})}^{k - 1} \end{aligned}$
::ak=10(- 15- 1)

$\begin{aligned} - \frac{10}{5^{11}} or - \frac{2}{5^{10}} \end{aligned}$
::-10511或-2510
$\begin{aligned} \frac{15}{2}, \frac{17}{2}, \frac{19}{2} \end{aligned}$

$\begin{aligned} a_{k} = \frac{7}{2} + (k - 1) \cdot 1 \end{aligned}$
::ak=72+(k- 1)%1
$\begin{aligned} \frac{633}{2} \end{aligned}$

$\begin{aligned} a_{k} = k^{3} + 3 \end{aligned}$
::ak=k3+3 公里=k3+3

Linear functions can be written in the form $\begin{aligned} f (x) = m x + b, \end{aligned}$ while arithmetic sequences can be defined as $\begin{aligned} a_{k} = d (k - 1) + a_{1} . \end{aligned}$ The common difference in an arithmetic sequence is like the slope, and the 1st term of the sequence is like the $\begin{aligned} y \end{aligned}$ -intercept. The reason for the $\begin{aligned} k - 1 \end{aligned}$ in the equation for the sequence has to do with the fact that we start sequences at term 1 instead of term 0. One difference between linear functions and arithmetic sequences is that arithmetic sequences are discrete (they exist only as specific values of the sequence), while linear functions are continuous.
::线性函数可以用 f( x) = mx+b 格式写成, 而算术序列可以定义为 ak=d( k-1)+a1. 算术序列中常见的差值与斜度相似, 而该序列的第一个条件则与 y intercut 类似。序列的方程中 k- 1 的原因与以下事实有关: 我们从 1 开始序列, 而不是从 0 开始。线性函数和算术序列之间的一个区别是, 算术序列是离散的( 它们仅作为序列的具体值存在), 而线性函数是连续的。

Exponential functions can be written in the form $\begin{aligned} f (x) = a \cdot b^{x}, \end{aligned}$ while geometric sequences can be defined as $\begin{aligned} a_{k} = a_{1} \cdot r^{k - 1} . \end{aligned}$ The common ratio in a geometric sequence is like the $\begin{aligned} b \end{aligned}$ value in an exponential function, and the 1st term in the sequence is like the $\begin{aligned} y \end{aligned}$ -intercept. The reason for the $\begin{aligned} k - 1 \end{aligned}$ in the equation for the sequence has to do with the fact that we start sequences at term 1 instead of term 0. One difference between exponential functions and geometric sequences is that geometric sequences are discrete (they exist only at the specific values of the sequence), while exponential functions are continuous.
::指数函数可以以 f( x) = abx 的形式写成, 而几何序列可以被定义为ak=a1rk-1。几何序列中的常见比率类似于指数函数中的值, 而该序列中的第一个术语则类似于y- interception。方程式中 k-1 的原理与以下事实有关: 我们从1号开始序列, 而不是从0号开始。指数函数和几何序列之间的一个区别是几何序列是离散的( 它们只存在于该序列的具体值上), 而指数函数是连续的。

a. $\begin{aligned} \frac{1}{4} \end{aligned}$ of a caramel
b. $\begin{aligned} 1, 1 \frac{1}{4}, and 1 \frac{1}{2} \end{aligned}$ caramels
::a. 1,114焦糖1,114和112焦耳中的14个

$\begin{aligned} 2^{10} or 1, 024 \end{aligned}$ aliens
::210或1,024 外国人

$\begin{aligned} 2^{15} or 32, 768 MB \end{aligned}$
::215或32,768MB

Section 13.4: Sigma Notation
::第13.4节:污名

-1 + 1 + 3 + 5 + 7 = 15
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 = 511
6 + 18 + 54 + 162 = 240
3 + 7 + 11 + 15 + 19 + 23 + 27 + 31 + 35 + 39 = 210
9 + 36 + 144 + 576 + 2,304 + 9,216 + 36,864 + 147,456 + 589,824 + 359,296 + 9,437,184 = 12,582,909

$\begin{aligned} \sum_{i = 0}^{7} 3 i + 1 \end{aligned}$
::i=073i+1

$\begin{aligned} \sum_{i = 0}^{4} 2 i + 3 \end{aligned}$
::i=042i+3

$\begin{aligned} \sum_{i = 0}^{7} - i + 8 \end{aligned}$
::i=07-i+8

$\begin{aligned} \sum_{i = 0}^{3} i + 5 \end{aligned}$
::i=03i+5

$\begin{aligned} \sum_{i = 0}^{\infty} 3 \cdot 2^{i} \end{aligned}$
::i=032i

$\begin{aligned} \sum_{i = 0}^{3} {10 \cdot (\frac{1}{2})}^{i} \end{aligned}$
::i=0310( 12) i

$\begin{aligned} \sum_{i = 0}^{\infty} 4 (- 2)^{i} \end{aligned}$
::i=044(-2)i

$\begin{aligned} \sum_{i = 0}^{\infty} 2 i + 2 \end{aligned}$
::i=02i+2

$\begin{aligned} \sum_{i = 0}^{\infty} {(\frac{1}{3})}^{i + 1} \end{aligned}$
::i=0(13)i+1

$\begin{aligned} \sum_{i = 0}^{\infty} 2 \cdot {(\frac{1}{3})}^{i + 1} \end{aligned}$
::i=02(13)i+1

Section 13.5: Arithmetic Series
::第13.5节:自学系列

1,128
11,016
6,885

1,584.3333 or $\begin{aligned} \frac{4, 753}{3} \end{aligned}$
::1 584.33333或4 7533

1,502.6666 or $\begin{aligned} \frac{4, 508}{3} \end{aligned}$
::1 502.666或4 5083
15,652
140,868
116,316
3,535
-47,429
-43,878
8,415
-69,636
384,750
-717,778.5

Section 13.6: Geometric Series
::第13.6节:几何系列

163,835
715,827,882
9.999694824
17.99999875
2,391,484.3333

Divergent
::差异

Divergent
::差异

Convergent; 10
::趋和; 10

Convergent; 18
::趋同; 18; 18

Divergent
::差异

Convergent; 9
::趋和; 9
$202,840.40
$3,144.07
$146,019.62

The terms in an arithmetic series can never approach zero, as they can in a geometric series.
::算术序列中的术语永远不会接近零,就像几何序列中的术语一样。

Section 13.7: Induction Proofs
::第13.7节:上岗证明

a. $\begin{aligned} 4 (5) = 20 \end{aligned}$ and $\begin{aligned} 2^{5} = 32 \end{aligned}$ ; $\begin{aligned} 20 < 32. \end{aligned}$
b. Assume $\begin{aligned} 4 k < 2^{k} . \end{aligned}$
c. Prove $\begin{aligned} 4 (k + 1) < 2^{k + 1} . \end{aligned}$
::a. 4(5)=20和25=32;20<32.b. Assume 4k < 2k. c. 证明4(k+1) < 2k+1。

a. $\begin{aligned} 8^{1} - 3^{1} = 8 - 3 = 5, \end{aligned}$ which is divisible by 5.
b. Assume $\begin{aligned} 8^{k} - 3^{k} \end{aligned}$ is divisible by 5.
c. Prove $\begin{aligned} 8^{k + 1} - 3^{k + 1} \end{aligned}$ is divisible by 5.
::a. 81-31=8-3=5, 可除以5. b. 8k-3k 的组号8k-3k 可除以5. c. 证明8k+1-3k+1可除以5。

a. $\begin{aligned} 7^{1} - 1 = 6, \end{aligned}$ which is divisible by 6.
b. Assume $\begin{aligned} 7^{k} - 1 \end{aligned}$ is divisible by 6.
c. Prove $\begin{aligned} 7^{k + 1} - 1 \end{aligned}$ is divisible by 6.
::a. 71-1=6, 可除以6. b. 7k-1的组装除以6. c. 证明7k+1-1除以6。

a. $\begin{aligned} 2^{2} = 4 \geq 4 = 2 (2) . \end{aligned}$
b. Assume $\begin{aligned} k^{2} \geq 2 k . \end{aligned}$
c. Prove $\begin{aligned} (k + 1)^{2} \geq 2 (k + 1) . \end{aligned}$
::a. 22=44=2(2).b. 代表k22k. c. 证明(k+1)2×2(k+1)。

a. $\begin{aligned} 4^{1} + 5 = 9 \end{aligned}$ , which is divisible by 3.
b. Assume $\begin{aligned} 4^{k} + 5 \end{aligned}$ is divisible by 3.
c. Prove $\begin{aligned} 4^{k + 1} + 5 \end{aligned}$ is divisible by 3.
::a. 41+5=9, 可除以 3. b. 4k+5 的组装可除以 3. c. 证明 4k+1+5 的组装可除以 3. c. 证明 4k+1+5 可除以 3.

a. $\begin{aligned} 0^{2} + 1^{2} = \frac{(1) (1 + 1) (2 (1) + 1)}{6} \end{aligned}$ (both sides equal 1)
b. Assume $\begin{aligned} 0^{2} + . . . + k^{2} = \frac{(k) (k + 1) (2 k + 1)}{6} . \end{aligned}$
c. Prove $\begin{aligned} 0^{2} + . . . + k^{2} + (k + 1)^{2} = \frac{(k + 1) (k + 2) (2 (k + 1) + 1)}{6} . \end{aligned}$
::a. 02+12=(1)(1+1)(2(1)+1)6 (两边各等1)b. 假设02+...+k2=(k)(k+1)(2k+1)(2k+1)6.c. 证明02+...+k2+(k+1)2=(k+1)(k+2)(2(k+1)+16)。

Inductive step:	$\begin{aligned} 4 k < 2^{k} \end{aligned}$
Add 4 to both sides:	$\begin{aligned} 4 k + 4 < 2^{k} + 4 \end{aligned}$
Logical reasoning:	$\begin{aligned} 4 < 2^{k} \end{aligned}$ since $\begin{aligned} k > 5 \end{aligned}$ ; therefore, $\begin{aligned} 2^{k} + 4 < 2^{k} + 2^{k} \end{aligned}$
Combine previous steps:	$\begin{aligned} 4 k + 4 < 2^{k} + 4 < 2^{k} + 2^{k} \end{aligned}$
Rewrite inequality:	$\begin{aligned} 4 (k + 1) < 2^{k} + 4 < 2^{k + 1} \end{aligned}$

::诱导步骤:4k <2k+4 <2k+4逻辑推理:4k+4 <2k+4逻辑推理:4k+2k自 k>5;因此,2k+4 <2k+2k组合先前的步骤:4k+4 <2k+4 <2k+4 <2k+2k+2kRewrite不平等:4(k+1) <2k+4 <2k+2k+1

Start with the statement you are trying to prove is divisible by 5:	$\begin{aligned} 8^{k + 1} - 3^{k + 1} \end{aligned}$
Add and subtract $\begin{aligned} 3 \cdot 8^{k} : \end{aligned}$	$\begin{aligned} 8^{k + 1} - 3 \cdot 8^{k} + 3 \cdot 8^{k} - 3^{k + 1} \end{aligned}$
Look for common factors:	$\begin{aligned} 8^{k} (8 - 3) + 3 (8^{k} - 3^{k}) \end{aligned}$
Simplify:	$\begin{aligned} 8^{k} (5) + 3 (8^{k} - 3^{k}) \end{aligned}$
	Since both parts of the expression are divisible by 5, the whole expression is divisible by 5.

::以您试图证明的语句开头, 5: 8k+1-3k+1+1+1+1+1+1+1+5: 8k+1- 3Q8k+3Q8k+3k+1减去 3Q8k+1 查找常见因数 : 8k( 8- 3)+3( 8k- 3k) 简化: 8k(5)+3( 8k- 3k) 因为表达式的两部分都可以除以 5, 整个表达式可以除以 5 。

Start with the statement you are trying to prove is divisible by 6:	$\begin{aligned} 7^{k + 1} - 1 \end{aligned}$
Add and subtract 7:	$\begin{aligned} 7^{k + 1} - 7 + 7 - 1 \end{aligned}$
Look for common factors:	$\begin{aligned} 7 (7^{k} - 1) + (7 - 1) \end{aligned}$
Simplify:	$\begin{aligned} 7 (7^{k} - 1) + (6) \end{aligned}$
	Since both parts of the expression are divisible by 6, the whole expression is divisible by 6.

::以您试图证明的语句开头,可以除以 6 : 7k+1-1+1 Add 和减去 7: 7k+1-7+7-1 寻找共同因素 7(7k- 1)+(7-1) 简化 7(7k- 1)+(6) 因为表达式的两个部分都可以除以 6, 整个表达式可以除以 6。

Statements we know:	$\begin{aligned} k^{2} \geq 2 k; 2 k \geq 1 \end{aligned}$
Reasoning:	$\begin{aligned} (k + 1)^{2} & = k^{2} + 2 k + 1 \geq 2 k + 2 k + 1 \geq 2 k + 1 + 1 = 2 k + 2 = 2 (k + 1) \end{aligned}$
Therefore:	$\begin{aligned} (k + 1)^{2} \geq 2 (k + 1) \end{aligned}$

::我们知道: k22k; 2k1 原因

k+1) 2= k2+2k+12k+2k+12k+1}2k+1+1=2k+2k+2k=2( k+1) 因此

k+1) 2x2( k+1) 因此

k+1) 2x2( k+1)

Start with the statement you are trying to prove is divisible by 3:	$\begin{aligned} 4^{k + 1} + 5 \end{aligned}$
Add and subtract 20:	$\begin{aligned} 4^{k + 1} + 20 - 20 + 5 \end{aligned}$
Look for common factors:	$\begin{aligned} 4 (4^{k} + 5) - 15 \end{aligned}$
Simplify:	$\begin{aligned} 4 (4^{k} + 5) - 3 (5) \end{aligned}$
	Since both parts of the expression are divisible by 3, the whole expression is divisible by 3.

::以您试图证明的语句开头, 3: 4k+1+5Add 和 20: 4k+1+20-20+5 减去 20: 4k+1+20-20+5 查找常见因素 4( 4k+5) - 15 简化: 4( 4k+5) - 3 (5) 因为表达式的两个部分 3 都可区分, 整个表达式 3 可区分。

Inductive step:	$\begin{aligned} 0^{2} + . . . + k^{2} = \frac{(k) (k + 1) (2 k + 1)}{6} \end{aligned}$
Add $\begin{aligned} (k + 1)^{2} \end{aligned}$ to both sides:	$\begin{aligned} 0^{2} + . . . + k^{2} + (k + 1)^{2} = \frac{(k) (k + 1) (2 k + 1)}{6} + (k + 1)^{2} \end{aligned}$
Manipulate the right side:	$\begin{aligned} 0^{2} + . . . + k^{2} + (k + 1)^{2} = \frac{(k) (k + 1) (2 k + 1) + 6 (k + 1)^{2}}{6} \end{aligned}$
Simplify the numerator of the right side:	$\begin{aligned} 0^{2} + . . . + k^{2} + (k + 1)^{2} = \frac{2 n^{3} + 9 n^{2} + 13 n + 6}{6} \end{aligned}$
Notice that the numerator of the right side that we want is $\begin{aligned} (k + 1) (k + 2) (2 (k + 1) + 1), \end{aligned}$ which simplifies to $\begin{aligned} 2 n^{3} + 9 n^{2} + 13 n + 6 \end{aligned}$	$\begin{aligned} 0^{2} + . . . + k^{2} + (k + 1)^{2} = \frac{(k + 1) (k + 2) (2 (k + 1) + 1)}{6} \end{aligned}$

::诱导步骤:02+...+k2=(k)(k)(k+1)(2k+1)+1)6 Add(k+1)2+(k+1)2+(k+1)2=(k)(k+1)2+(k+1)6+(k+1)2=(k)(k)(k+1)(2k+1)1+6(k+1)+6(k+1)26 简化右侧的计数器: 02+...+k2+(k+1)2+(k+1)2+K2+(k+1)2+(k+1)2=(k+2(k+1)+66+(k)(k+1)+1) 右侧的计数器:02+...+k(k)(k)(k+1)(k+1)(2k+1)26 简化右侧的计数器: 02+k2+(k+1)(k+1)(k+1)(k+2)(k+2)(k)(k)2(k)(2)(k)2(k)(2)(k+1)+1)+1)+1)6-6)

You cannot find a base case to prove it's true.
::你不能找到一个基本案例来证明这是真的

The base case is necessary for showing that the statement is true at least once. The inductive step then shows that for every number for which the statement is true, the statement is also true for the following number. Because the base case is true, then the statement must be true for all numbers. Without the base case, you haven't proven anything!
::要显示该语句至少真实一次, 基本语句是必需的。那么, 暗示性步骤可以显示, 对于每一个语句真实的数字, 该语句对下一个数字也是真实的。由于基本语句是真实的, 那么语句对所有数字都必须是真实的。没有基础语句, 您没有证明什么 !

Base case: For n = 3, the sum of the angles in a triangle is 180° by the Triangle Sum Theorem from geometry.
Inductive step: Assume an $\begin{aligned} n \end{aligned}$ -gon has interior angles with a sum of $\begin{aligned} 180 (n - 2) \end{aligned}$ .
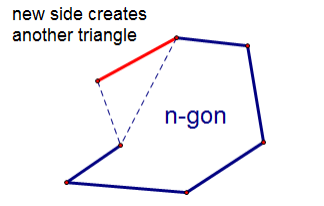
Proof: We want to show that the sum of the interior angles of an $\begin{aligned} n + 1 \end{aligned}$ -gon is $\begin{aligned} 180 (n + 1 - 2) \end{aligned}$ . An $\begin{aligned} n + 1 \end{aligned}$ -gon will have one additional side compared to an $\begin{aligned} n \end{aligned}$ -gon. This means that one additional triangle can be drawn connecting exterior vertices. This logic is shown in the picture below.

The additional triangle adds another 180 degrees to the sum of the interior angles. This means an $\begin{aligned} n + 1 \end{aligned}$ -gon has interior angles with a sum of $\begin{aligned} 180 (n - 2) + 180 \end{aligned}$ . This can be rewritten as $\begin{aligned} 180 (n + 1 - 2) \end{aligned}$ .
::对于 n = 3 , 三角形中角的和值为 180 度, 三角形中角的和值为三角形 Sum 理论从几何中绘制 180 度。诱导步骤 : 以 n- 2 表示内角为 180( n-2 ) 。证明 : 我们要显示 n+1- gon 内角的和值为 180 ( n+1- 2-2) 。 n+1- gon 与 n- gon 相比, 内角的和值为 180 ( n+1-2) +180 。这表示可以再绘制一个三角形, 连接外部顶部。此逻辑在下图中显示。额外三角形向内角的和值增加 180 。这意味着 n+1- g 的内角为内角, 内角的和值为 180 ( n- 2) 。这可以重写为 180 ( n+1-2) 。

章节大纲

常规

答复----第13章:序列和系列

Section 13.2: Recursion ::第13.2节第13.2节:再货

Section 13.3: Arithmetic and Geometric Sequences ::第13.3节:测量和几何序列

Section 13.4: Sigma Notation ::第13.4节:污名

Section 13.5: Arithmetic Series ::第13.5节:自学系列

Section 13.6: Geometric Series ::第13.6节:几何系列