课程： 2.4 等同等同 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节异同等同

折叠展开
异同等同
If you have ever studied differential equations then you can solve homogeneous systems of first order differential equations to solve for a function. In Linear Algebra we have a vague analogue of that problem also called a homogeneous system where we have to solve a linear system where all of the values to the right of the augment are 0. Essentially we have the equation $\begin{aligned} A \vec{x} = \vec{0} \end{aligned}$ .
::如果您曾经研究过差异方程式, 那么您就可以解开一阶差方程式的同质系统, 以解答函数。在线性代数中, 我们有一个关于这个问题的模糊相似性, 也称为同质系统, 我们必须解决一个线性系统, 其所有值均值均值为 0。基本上, 我们有了 Ax\\\\\\\\\\\\ 等方程式。

This equation is extremely interesting, because it essentially tells us whether or not the columns of A are linearly dependent or independent.
::这一方程式非常有趣,因为它基本上告诉我们A栏是否线性依赖或独立。

L ike we always do before looking at theorems and lemmas, let's try our a few examples and try to get a feel for what we are doing.
::就像我们总是在研究理论和莱姆马斯之前做的一样, 让我们尝试几个例子, 试着了解我们在做什么。

Let's take the system
::让我们采取系统

$\begin{aligned} 3 x_{1} + 4 x_{2} - 2 x_{3} = 0 \\ - 2 x_{1} + 5 x_{2} + x_{3} = 0 \\ 7 x_{1} - 2 x_{2} - 4 x_{3} = 0 \end{aligned}$ .
::3x1+4x2-2x3=0-2x1+5x2+x3=07x1-2x2-4x3=0。

Obviously there is a solution in $\begin{aligned} x_{1} = x_{2} = x_{3} = 0 \end{aligned}$ . However, we have to apply elimination to make sure that this system has 1 and only 1 solution. This is because if we find another solution then there are infinite solutions and we can find a linear dependence relation among the columns.
::显然在 x1=x2=x3=0 中有一个解决方案。但是, 我们必须使用删除方法以确保这个系统有1个且只有1个解决方案。这是因为如果我们找到另一个解决方案, 那么就会有无限的解决方案, 我们可以在列中找到线性依赖关系。

Isolating $\begin{aligned} x_{3} \end{aligned}$ to get $\begin{aligned} x_{2} \end{aligned}$ as a function of $\begin{aligned} x_{3} \end{aligned}$ we get $\begin{aligned} x_{2} = \frac{x_{3}}{23} \end{aligned}$ and after you plug back in and do some algebraic manipulation to get $\begin{aligned} x_{3} = x_{2} = x_{1} = 0. \end{aligned}$
::隔离 x3 以获得 x2 作为 x3 的函数, 我们得到 x2=x323 并在您插入后进行代数操作以获得 x3=x2=x1=0 。

This essentially means that there is only a trivial linear dependence relation and hence none at all. Thus the columns of the matrix A in what would be the matrix vector equation Ax = b would span the reals in 3 dimensions.
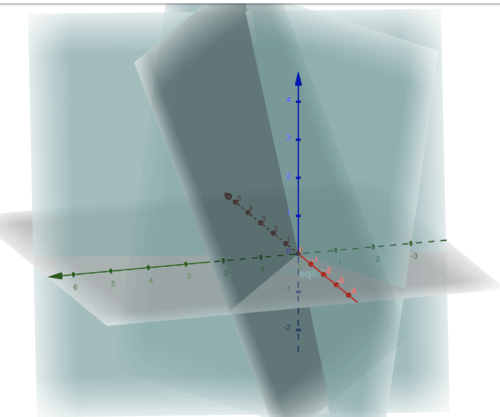
::这基本上意味着只有微不足道的线性依赖关系,因此根本就没有。因此,矩阵矢量方程式Ax=b中的矩阵A列将覆盖三个维度的实数。

For sake of continuity we get the geometric picture of:

::为了保持连续性,我们可以看到几何图画:

Now when the homogeneous system has infinitely many solutions it is the case that there are either the entire set of solutions in a line that is the intersection of two planes or just as a matter of fact a plane. This means that if there are more variables than equations in a homogeneous system of linear equation that there are infinitely many solutions.
::当同质系统拥有无限多的解决方案时,就是在两平面交点的线条中存在一整套解决方案,或者事实上存在一平面。这意味着如果在线性等式的同质系统中存在比方程更多的变量,那么就有很多解决方案。

In some cases you'll still see the same amount of equations as variables, but it will usually be the case that two of those equations are the same and/or are scalar multiples of each other.
::在某些情况下,你仍然会看到相同数量的方程式作为变量, 但通常情况下,其中两个方程式是相同的, 并且(或者)是相互的卡路里倍数。

Let's first look at a couple of examples. Take the system
::让我们首先看看几个例子。采用这个系统

$\begin{aligned} 3 x_{1} + 4 x_{2} + 7 x_{3} = 0 \\ x_{1} + 2 x_{2} + 3 x_{3} = 0 \\ 2 x_{1} - 5 x_{2} - 3 x_{3} = 0 \end{aligned}$ .
::3x1+4x2+7x3=0x1+2x2+3x3=02x1-5x2-3x3=0。

Here you also get infinitely many solutions, because if you take this into a matrix vector product you see that the sum of the first two columns of A is the third column, so the total span is the span of the first two columns with a linear dependence relationship.
::您在这里还得到了无限多的解决方案, 因为如果您把这个输入到矩阵矢量产品中, 您就会看到 A 前两列的总和是第三列, 所以总长度是前两列的宽度, 与直线依赖关系。

Geometrically, you get the picture of these planes all intersecting in a line:
::从几何上看,你可以看到这些飞机的相交线线是:

It is impossible to have no solutions to a homogeneous system of linear equations. Think about it. There has to be at least one solutions, the trivial solution. So to a homogeneous equation there are either infinite solutions or one solution.
::无法对线性方程式的同质系统找到解决方案。想想它。必须至少有一个解决方案, 一个小的解决方案。所以对于一个同质方程式, 要么有无限的解决方案, 要么只有一个解决方案。

Claim: A matrix is invertible if and only if the only solution to Ax = 0 is the trivial solution.
::索赔:如果而且只有在Ax = 0的唯一解决办法是微不足道的解决办法时,矩阵是不可倒置的。

1. First, we show the proof that if there is only the trivial solution then the matrix is invertible.
::1. 首先,我们证明,如果只有微不足道的解决办法,那么矩阵是不可置疑的。

This means that there is only one solution and so the columns are linearly independent because there is no nontrivial linear dependence relation.
::这意味着只有一个解决办法,因此各列是线性独立的,因为没有非两端线性依赖关系。

2. Then show that if A is invertible then there is only the trivial solution.
::2. 然后证明,如果A是不可倒置的,那么只有微不足道的解决办法。

If A is invertible than we can multiply both sides of the equation by A^-1 to get x = A^-1 times the zero vector. And any matrix times the zero vector yields the zero vector so hence x is the trivial solution and that is the only solution.
::如果 A 是不可倒置的, 则无法将方程的两边乘以 A = 1 乘以 A = 1 乘以 0 向量。任何矩阵乘以 0 向量使零向量产生零向量 , 因此 x 是微不足道的解决方案, 这是唯一的解决方案。

This is just one part of what we call the invertible matrix theorem which we'll discuss later which shows dozens of equivalent conditions that show whether or not a matrix is invertible.
::这只是我们称之为“垂直矩阵理论”的一部分,我们稍后将讨论这些理论,其中显示数十种同等条件,表明一个矩阵是否是不可倒置的。

Right now we have the case that if the columns are linearly dependent then the matrix is not invertible. We can show that this implies that the matrix has determinant 0.
::我们现在的情况是,如果柱子线性依赖,则矩阵是不可倒置的。我们可以证明,这意味着矩阵有决定性值0。

There are two main ways to do this, algebraically and geometrically.
::这样做有两个主要方法,代数和几何方法。

Looking at this in two dimensions, you can recall that two vectors where linearly dependent if and only if they were scalar multiples of each other. Hence if you have two column vectors of the form $\begin{aligned} [\begin{matrix} a \\ b \end{matrix}], [\begin{matrix} c a \\ c b \end{matrix}] \end{aligned}$ putting it into a matrix form you would get $\begin{aligned} [\begin{matrix} a & c a \\ b & c b \end{matrix}] \end{aligned}$ then the determinant comes out to be $\begin{aligned} a c b - b c a = a c b - a b c = 0 \end{aligned}$ .
::从两个维度来看,您可以记得,两个矢量线性依赖两个矢量,如果并且只有在两个矢量是星标的倍数时才线性依赖。因此,如果有两种以表[ab]为列矢量的矢量,[cacb] 将其放入矩阵表,您就会得到[acabcbb],那么决定因素就是 acb-bca=acb-abc=0。

Now for the three by three case we have the columns linearly independent if they take the form of either one vector or two vectors composing the span of the columns of the matrix. First, for the one vector case, we have the trivial idea of $\begin{aligned} det ([\begin{matrix} c_{1} & a c_{1} & b c_{1} \\ c_{2} & a c_{2} & b c_{2} \\ c_{3} & a c_{3} & b c_{3} \end{matrix}]) \end{aligned}$ . This comes out to be $\begin{aligned} c_{1} (a c_{2} b c_{3} - a c_{3} b c_{2}) - a c_{1} (c_{2} b c_{3} - b c_{2} c_{3}) + b c_{1} (c_{2} a c_{3} - c_{3} a c_{2}) = 0 c_{1} - 0 a c_{1} + 0 b c_{1} = 0 \end{aligned}$
::现在,对于三三三三立立案,如果柱体的形式是组成矩阵柱体的柱体的一矢量或两个矢量,则具有线性独立。首先,对于一个矢量的立体,我们有一个微不足道的点点点([c1ac1bc1c2c2c2c2c2c2c2c3c3c3b3c3c33]) 。它出来为 c1(c2bc3-ac3b3bc2c3)-ac1(c2b3-bc2c3)+bc1(c2ac3-c3c3)=0c1-0ac1+0bc1=0)

Now for the two linearly independent column vectors case we have to do a little bit more work and end up taking
::现在,对于两个线性独立的柱体矢量,我们必须多做一点工作,最终要花很多时间

$\begin{aligned} det ([\begin{matrix} c_{1} & d_{1} & x c_{1} + y d_{1} \\ c_{2} & d_{2} & x c_{2} + y d_{2} \\ c_{3} & d_{3} & x c_{3} + y d_{3} \end{matrix}]) = c_{1} | \begin{matrix} d_{2} & x c_{2} + y d_{2} \\ d_{3} & x c_{3} + y d_{3} \end{matrix} | - d_{1} | \begin{matrix} c_{2} & x c_{2} + y d_{3} \\ c_{3} & x c_{3} + y d_{3} \end{matrix} | + (x c_{1} + y d_{1}) | \begin{matrix} c_{2} & d_{2} \\ c_{3} & d_{3} \end{matrix} | \end{aligned}$
:[c1d1xc1+yd1c2d2x2+yd2c3x3+yd3]) (c1+d2x2+yd2d3x3+yd3+yd3+yd3+yd1+c2x2+yd3x3+yd3x3+yd3x3+yd3+yd3c3x3+yd3}(xc1+yd1+yd1)\\c2d2c3d3\\\\\\\c2d

Simplifying comes out to $\begin{aligned} c_{1} (d_{2} (x c_{3} + y d_{3}) - d_{3} (x c_{2} + y d_{2})) - d_{1} (c_{2} (x c_{3} + y d_{3}) + c_{3} (x c_{2} + y d_{3})) + (x c_{1} + y d_{1}) (c_{2} d_{3} - c_{3} d_{2}) = 0. \end{aligned}$
::简化出来到 c1 (d2( x2( xc3+yd3)- d3( xc2+yd2))- d1 (c2( x2( xc3+yd3)+c3( xc2+yd3))+( xc1+yd1)(c2d3 - c3d2)=0。

Now we've seen all of these have no determinant. Now we can see this geometrically to get:
::现在我们已经看到所有这些没有决定性因素。现在我们可以从几何角度看到:

For the 2x2 case
::2x2 案件

Here, when you see that these two vectors span a line, so when you take a linear combination of the columns you can only stay on one line and you cannot take the inverse of the matrix. You cannot reverse the process to get a unique solution or in some cases any solutions for that matter.
::这里, 当您看到这两个矢量横跨一条线条时, 所以当您对列进行线性组合时, 您只能停留在一条线上, 您不能对矩阵进行反向。您无法将进程倒转, 以获得一个独特的解决方案, 或者在某些情况下, 任何解决方案。

For the 3x3 case with one vector, we have the exact same idea, but just in 3 dimensions:
::对于一个矢量的 3x3 案例, 我们有一个完全相同的想法, 但是仅仅在 3 维上:

Next for the 3x3 case with 2 vectors, we have a similar analogue to the 2 dimension case; however, there is a plane spanned in three dimensions. Similarly to the 2 dimensional case you have a third vector that gives you a system of equations that has either infinite or no solutions and the process is not reversible geometrically. Play with it here:
::3x3 例与 2 矢量 3 相继, 我们与 2 维量相类似; 但是, 平面横跨三维。与 2 维 3 向量相类似, 您拥有第三个向量 , 给您一个公式系统, 它要么无限, 要么没有解决方案, 而这个过程不是可逆的几何。在此使用它 :

Add some vectors and see why there is no way to reverse any linear combination taken.
::添加一些矢量,看看为什么没有办法扭转任何线性组合。

章节大纲

常规

异同等同