1.2 代表线性职能-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 代表线性函数

  Collapse Expand

  代表线性函数

  播放段落

  The Purpose of  This Lesson
  ::本课程的目的

  In this lesson, you will use to model scenarios. Linear functions are represented using tables, equations, and graphs. You will also write and solve equations to answer questions about linear functions. 

  播放段落

  Introduction: E quations , T ables , and  G raphs   of  L inear Functions
  ::导言:线性函数的方形、表格和图表

  Functions can be represented in multiple ways. One useful way to write a linear equation is   slope-intercept form :  $\begin{array}{r}y=mx+b\end{array}$ . The and y-intercept can be drawn from a  table or graph of a linear function . You  can answer questions about one or more linear functions by looking at their graphs, working with their tables, or writing and solving equations .

  

  播放段落

    Representing Functions
  ::代表职能

  播放段落

  Functions may be represented as tables, equations, or graphs.
  ::函数可按表格、方程式或图表表示。

  播放段落

  Different types of representations are more efficient for different uses, and information from one type of representation may be used to create a different type.
  ::对于不同用途而言,不同类型的表述方式更有效率,一种类型的表述方式的信息可用于创建不同类型的表述方式。

  播放段落
  • Graphing : Graphing a linear function can help visualize the relationship between two variables and make predictions about future values. It can also be used to identify patterns and trends in data, such as in financial or scientific data.
    ::绘图:绘制线性函数的图解可以帮助对两个变量之间的关系进行可视化分析,并对未来值作出预测,还可以用来确定数据模式和趋势,如财务或科学数据。
  播放段落
  • Writing a function : Writing a linear function in the form of an equation can help make calculations and predictions based on specific values. It can also be used in optimization problems, such as finding the maximum or minimum value of a function.
    ::写入函数 : 以等式形式写入线性函数有助于根据具体值进行计算和预测。它也可以用于优化问题,例如找到函数的最大值或最小值。
  播放段落
  • Creating a table of values : Creating a table of values for a linear function can help identify specific points on the graph and can be used to interpolate or extrapolate data. It can also be used to find the slope and y-intercept of a linear function.
    ::创建数值表:为线性函数创建数值表有助于确定图形上的具体点,并可用于内推或外推数据。也可以用来查找线性函数的斜度和 Y 界面。

  ---

  播放段落

  Activity 1: Solve Using Equations, Tables, and Graphs
  ::活动1:使用等号、表格和图表解决

  播放段落

  Example 1-1
  ::例1-1

  Suppose your friend Janelle encounters a  wizard. She tells you that she gave this wizard 5 blueberries, and the wizard returned 16 of them. Then she gave the wizard 7 blueberries and the wizard returned 22.   Given that the  wizard's behavior is modeled by a linear function, find  a representation for the function , and use it to predict the number of blueberries this wizard will return if Janelle gives her 10. Describe the method you used.

   

  播放段落

  Solution:   There are several ways to approach this problem. First, let $\begin{array}{r}x\end{array}$  represent the number of blueberries given and $\begin{array}{r}y\end{array}$  the number returned. 
  ::解决方案: 解决这个问题有几种方法。 首先, letx 代表给定的蓝莓数量, 返回的数字是 Andy 。

  播放段落

  Method 1
  ::方法1

  Here is a table of the given data:

  $$\begin{array}{r}\begin{array}{cc}x& y\\ 5& 16\\ 7& 22\end{array}\end{array}$$

  播放段落

  The slope is 3, so extend the table as shown below to determine the number returned for an $\begin{array}{r}x\end{array}$  value of 10:
  ::斜坡为 3, 将表格展延如下, 以确定以 10 的 Anx 值返回的数值 :

  $$\begin{array}{r}\begin{array}{cc}x& y\\ 5& 16\\ 7& 22\\ 8& 25\\ 9& 28\\ 10& 31\end{array}\end{array}$$

  
  

  播放段落

  Method 2
  ::方法2

  播放段落

  Another option is to first find the equation of the line. You know the slope is 3:
  ::另一个选择是首先找到线的方程。你知道斜坡是3:

  $$\begin{array}{r}\begin{array}{ll}\text{Step}& \text{Explanation}\\ y=mx+b& \text{Slope-intercept form for a line.}\\ y=3x+b& \text{The slope, }m,\text{ is}3.\\ 16=3(5)+b& (5,16)\text{is a point on the line.}\\ b=1& \text{Solving for}b.\\ y=3x+1& \text{The equation for the line.}\end{array}\end{array}$$

   

  You want to know the $\begin{array}{r}y\end{array}$  value returned for an $\begin{array}{r}x\end{array}$   value of 10. So substitute 10 for  $\begin{array}{r}x,\end{array}$   and find  $\begin{array}{r}y:\end{array}$

  $$\begin{array}{r}\begin{array}{l}y=3(10)+1\\ y=31\end{array}\end{array}$$

  播放段落

  Method 3
  ::方法3

  播放段落

  You can also graph the line and try to visually determine the $\begin{array}{r}y\end{array}$  value that corresponds to an $\begin{array}{r}x\end{array}$  value of 10:
  ::您也可以绘制线条图,并尝试以视觉方式确定其值,与 10 的 Anx 值相对应:

  

  播放段落

  PLIX Interactive
  ::PLIX 交互式互动

  ---

  播放段落

  Activity 2: Write  and Solve Equations to Answer Function Questions
  ::活动2:写作和解析等号以解答函数问题

  In previous courses, you learned how to solve linear equations. In high school, you will still frequently solve linear equations. Often, you will write and solve linear equations to answer questions about functions. Sometimes, you will write an equation involving two functions in order to understand the relationship between them.

  播放段落

  Example 2-1
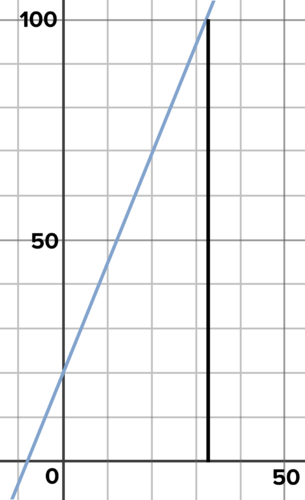
  ::例2-1

  Imagine you encounter the wizard whose graph is shown below. Suppose you want her to return 100 blueberries. How many should you give her? Explain your process. Is your result an estimate or an exact solution? If it's an estimate, what information would help you find an exact solution?

  播放段落

  Solution:  There are several ways to approach the problem. First, let  $\begin{array}{r}x\end{array}$  represent the number of blueberries given and  $\begin{array}{r}y\end{array}$  represent the number of blueberries returned. 
  ::解决方案: 解决问题有几种方法。 首先, x 代表给定的蓝莓数量, y 代表返回的蓝莓数量 。

  播放段落

  Method 1
  ::方法1

  播放段落
  • From the graph, the $\begin{array}{r}y\end{array}$ - intercept appears to be 20. 
    ::从图中看,它们似乎有20个被拦截。
  播放段落
  • The graph also appears to go through the point (20, 70).
    ::图表似乎也经过了点(20、70)。
  播放段落
  • Using the procedure described previously, you arrive at the equation  $\begin{array}{r}y=\frac{5}{2}x+20\end{array}$ .
    ::使用前述程序,您可以到达y=52x+20的方程。
  播放段落
  • To find the $\begin{array}{r}x\end{array}$  value that returns a $\begin{array}{r}y\end{array}$  value of 100, substitute 100 for  $\begin{array}{r}y\end{array}$ , and solve:
    ::要找到返回 Ay 值为 100 的x 值, 替换 Y 的 100, 并解决 :

  播放段落

  $$\begin{array}{rl}100& =\frac{5}{2}x+20\\ 80& =\frac{5}{2}x\\ 160& =5x\\ x& =32\end{array}$$

  
  ::100=52x+2080=52x160=5xxx=32

  播放段落

  Method 2
  ::方法2

  播放段落

  Although imprecise, you can see from the graph that the $\begin{array}{r}x\end{array}$  value that returns a $\begin{array}{r}y\end{array}$  value of 100 is between 30 and 40, and closer to 30 than to 40:
  ::虽然不精确,但从图表中可以看出,返回 Ay 值为 100 的x值在 30 至 40 之间, 接近 30 至 40 之间 :

  

  播放段落

  Notice on the graph that an x-value in the low 30s returns a y-value of 100.
  ::图表上的注意, 最低 30 值中的 x 值返回 100 y 值 。

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. Given below are the equations for two wizards. What number of blueberries given to each will cause them both to return the same amount? How did you arrive at your answer?
     $$\begin{array}{r}y=\frac{1}{2}x+7\\ y=2.5x-12\end{array}$$
     
     ::下面给出两个向导的方程。 给每个向导给多少蓝莓才能让他们返回相同数量 ? 您是如何找到答案的 ? y= 12x+7y=2.5x- 12
  播放段落
  2. The following equation can help us find the answer to the last question. Why? Solve this equation to determine the value that will return the same value for both functions. Then, determine the value that corresponds to this value. Write the and value you found as an ordered pair , that is, a point. What does this point represent?
     $$\begin{array}{r}\frac{1}{2}x+7=2.5x-12\end{array}$$
     
     ::以下方程可以帮助我们找到最后一个问题的答案 。 为什么 ? 解答此方方程以决定返回两个函数的相同值。 然后, 确定与此值对应的值。 写入您找到的一对定购的值, 也就是一个点。 此点代表什么? 12x+7=2.5x- 12
  播放段落
  3. This lesson has used the blueberry wizard scenario to explore linear functions, their representations, and equations to answer questions about them. Think of 5 other scenarios in the world where a numerical input produces a corresponding numerical output. Come up with an equation to represent each scenario, and explain the meaning of each part of the equation. Decide if a table, equation, or graph is the best way to represent each function, and explain why.
     ::此课程使用蓝莓向导假想来探索线性函数、它们的表达方式和方程式来解答关于它们的问题。 想想世界上有5种其他的假想, 数字输入产生相应的数字输出。 以方程式来代表每个假想, 并解释方程式每个部分的含义。 决定一个表格、 方程式或图形是代表每个函数的最佳方式, 并解释原因 。
  播放段落
  4. Not all functions are linear. Create equations for five non-linear functions.
     ::并非所有函数都是线性函数。为五个非线性函数创建方程式。
  播放段落
  5. The following is a table showing some essential questions that you will often seek to answer about functions. Discuss the meaning of each in the context of the blueberry wizard scenario.
     ::下表显示了您经常试图回答的一些关于函数的基本问题。在蓝莓向导情景中讨论每个功能的含义。

  播放段落

      Essential Questions about Functions
  ::关于职能的基本问题

  播放段落 Given one function: ::赋予一个函数 : 播放段落 What input returns an output of ___? What output is returned for an input of ___? ::什么输入返回 __ 的输出?什么输出返回 __ 的输入返回 ?

  播放段落 Given two functions:  ::赋予两项职能: 播放段落 What single input will produce the same output for both functions? What output does the input above produce? ::两种函数的单一输入将产生相同的输出?上述输入产生什么样的输出?

  播放段落

  PLIX Interactive
  ::PLIX 交互式互动

  播放段落

    Summary
  ::摘要

  播放段落
  • Linear functions may  be represented with tables, equations, and graphs.
    ::线性函数可用表格、方程式和图表表示。
  播放段落
  • Each representation can be converted to any other in order to help visualize relationships and solve problems.
    ::每个代表可以转换为任何其他代表,以帮助直观地看待关系和解决问题。
  播放段落
  • Writing and solving equations may  answer questions about functions. 
    ::书写和解答方程式可以回答有关功能的问题。

  播放段落

  PLIX Interactive
  ::PLIX 交互式互动