课程： 3.1 界定职能-interactive | The Way To Learn

The Way To Learn

首页日程管理

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节界定职能

折叠展开
界定职能
The Purpose of this Lesson
::本课程的目的

In this lesson, you will learn to represent functions using function notation. You will formally define a function and learn how to describe the values a function accepts as input and the values it returns as output.
::在此课程中, 您将学习使用函数符号来代表函数。您将正式定义函数, 并学习如何描述一个函数所接受的作为输入的值及其返回的作为输出的值。

Introduction: Functions
::导言:职能

Distance is a function of time traveled

In the past two chapters, you've explored several types of functions. You've described one quantity as a function of another. In many cases, the relationship between two quantities is causal . For example, the distance a car has traveled is a function of the passage of time and not the other way around. The number of gallons of gasoline a refinery produces is a function of the amount of oil it takes in and not the other way around. In this case, the amount of oil is called the independent variable , and the amount of gasoline is the dependent variable.
::在过去的两章中, 您已经探索了几种功能。您描述了一个数量是另一个函数的函数。在许多情况下, 两个数量之间的关系是因果的。例如, 汽车行驶的距离是时间流逝的函数, 而不是相反。炼油厂生产的汽油加仑数是石油量的函数, 而不是反过来的函数。在这种情况下, 石油量被称为独立变量, 汽油量是依附变量。

Activity 1: Independent and Dependent Variables
::活动1:独立和依赖变量

Example 1-1
::例1-1

For each of the following pairs of quantities, determine which quantity should be the independent variable and which should be the dependent variable. Explain your decision. State the relationship by completing the sentence: _________ is a function of __________. Describe how the dependent variable changes as the independent variable changes. If possible, sketch a potential graph of the relationship. Discuss what function type might best model your graph.
::对于以下每一对数量, 确定哪个数量应该是独立的变量, 哪个应该是独立的变量。请解释您的决定。请通过补充句子来说明关系 : __% 是的函数。描述依赖的变量如何变化作为独立的变量的变化。如果可能的话, 请绘制一个可能的关系图。讨论哪个函数类型可以最佳地模拟您的图表。

The time it takes to get home; the amount of traffic.
::回家所需时间;交通量。

The amount of time dedicated to studying; the grades received.
::用于学习的时间;获得的年级。

The number of rainy days in a city per year; the number of umbrellas sold there.
::每年一个城市的雨日数;在那里出售的雨伞数。

The number of people at the beach; t he number of people on summer vacation.
::海滩上的人数;暑假的人数。

Sun exposure; plant growth rate .
::太阳照射;植物增长率。

Amount of food eaten by a cat; the m ass of the cat.
::猫吃的食物数量; 猫的质量。

The probability of snow; air temperature.
::雪的概率; 空气温度。

The amount of grass available; the population of deer.
::可用草的数量;鹿人口。

Sailboat length; top speed of sailboat.
::帆船长度;帆船最高速度。

Hour of the day; the number of donuts left in a donut shop.
::一天到晚,甜甜圈店里留下的甜甜圈数量。

Solution: There are alternative interpretations to those provided below, but here are some ways to think about each scenario.
::解决办法:除下文提供的解释外,还有其他解释,但这里有一些方法来考虑每一种情况。

The time it takes to get home is a function of the amount of traffic. The time it takes is the dependent variable; the amount of traffic is the independent variable. As the amount of traffic increases, the time to get home increases.
::回家所需时间是交通量的函数。时间是依附变量;交通量是独立的变量。随着交通量的增加,回家的时间会增加。

The grades received is a function of the time spent studying. Grades are the dependent variable, time spent studying is the independent variable. As time spent studying increases, grades increase, but only to a point - above a certain number of hours, increasing studying further actually causes grades to decline.
::获得的成绩取决于学习时间,年级是依附变量,学习时间是独立的变量,学习时间随着学习时间的增加而增加,但只达到一个点 -- -- 超过一定的时数,学习时间的增加实际上导致年级下降。

The number of umbrellas sold is a function of the number of rainy days per year. As rainy days increase, the number of umbrellas sold increases.
::出售伞的数量取决于每年雨季的数量,随着雨季的增加,出售伞的数量也随之增加。

The number of people at the beach is a function of the number on summer vacation. As the number of people on summer vacation increases so does the number of people at the beach.
::海滩上的人数取决于暑假的人数,随着暑假人数的增加,海滩上的人数也随之增加。

Plant growth is a function of sun exposure. As the sun exposure increases, the plant growth increases, up to a point. It is possible that too much sun decreases plant growth at some point.
::植物生长是太阳照射的函数。随着太阳照射的增加,植物生长会增加,甚至达到一个点。太阳过量可能会在某个时候降低植物生长。

The mass of a cat is a function of the amount of food eaten. As the food eaten increases, so does the mass of the cat.
::猫的重量取决于所食食物的数量。随着食物的吃量增加,猫的重量也随之增加。

The probability of snow is a function of the air temperature. The probability may be lower when it's extremely cold, as such temperatures are associated with dry conditions. As the temperature increases, the probability should be pretty stable, until the temperature approaches and passes the freezing point of water. After this value, the likelihood of snow should tumble close to 0.
::雪的概率是空气温度的函数。当它极冷时, 概率可能更低, 因为这样的温度与干燥条件相关。随着温度的上升, 概率应该相当稳定, 直到温度接近和通过水的冷点。在此值之后, 雪的概率会跌至接近0 。

The deer population is a function of grass available. As the available grass increases so does the deer population. You could argue that late in the season, the grass available might be a function of the deer population - a high population of deer can consume the grass and decrease the grass available.
::鹿口是可用草的产物,随着可用草量的增加,鹿口也会增加。你可以争辩说,在季节末期,可用草量可能是鹿口的产物,鹿口高,可以食用草量,减少可用草量。

The speed of the boat depends on the length of the sailboat. The actual function is a square root function .
::船舶的速度取决于帆船的长度,实际功能是平方根函数。

The number of donuts left is a function of the hour of the day. A donut shop opens with donuts on the shelves, but it's quickly making more. Eventually, they slow production and hope to sell out their supply by the end of the day.
::剩下的甜甜圈数量随时间变化。甜甜圈店开着, 书架上有甜甜圈, 但它正在迅速增加。最后, 它们减慢了生产速度, 并希望在一天结束时卖掉它们的供应。

Activity 2 : Using Function Notation
::活动2:使用函数标记

Example 2-1
::例2-1

You've written many equations to represent functions in the course so far. Write an equation (using function notation if possible) to represent the following scenario: Jamal is a gardener who wants to grow some apple trees. He only has space for a maximum of 10 trees. It will cost $250 to purchase the necessary mulch and fertilizer to prepare the soil. Beyond that, Jamal expects to pay $75 per tree in natural herbicides, water, and other costs.
::您已经写了许多方程式来代表课程中的函数。写一个方程( 可能的话使用函数标记) 来代表以下情景 : Jamal 是一位园丁, 想要种植一些苹果树。他只有最多10棵树的空间。购买必要的沼气和肥料来准备土壤需要花费250美元。除此之外, Jamal还要支付每棵树75美元的天然除草剂、水和其他费用。

Jamal has $525 to work with. Enter different numbers of trees in the interactive below to determine the number of trees Jamal can grow without exceeding $525, then c reate a function that models the cost of Jamal's orchard as a function of the number of trees. Use the function to predict the cost for 7 trees. Write and solve an equation to determine the largest number of trees Jamal can grow without exceeding $525.
::Jamal 需要工作525美元。请在下面互动处输入不同数目的树木, 以确定Jamal可以种植的树木数量, 但不超过525美元, 然后建立一个函数, 将Jamal 果园的成本作为树木数量的函数。使用此函数来预测 7 棵树的成本。写入和解析一个方程, 以确定Jamal 能够种植的树木数量最多, 不超过 525美元。

INTERACTIVE

Defining Functions

Enter in different numbers of trees into the interactive below to help you find the answer.
::以不同数目的树进入下面的交互关系中,帮助您找到答案。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Solution: The function is: $\begin{aligned} y = 75 x + 250. \end{aligned}$
::解析度: 函数为: y=75x+250 。

To represent this using function notation , begin by writing:
::要用函数符号表示此功能,首先要以书面形式表示:

$\begin{aligned} y = f (x) = 75 x + 250 \end{aligned}$

::y=f(x)=75x+250

The expression $\begin{aligned} f (x) \end{aligned}$ doesn't mean multiplication . It's read " $\begin{aligned} f \end{aligned}$ of $\begin{aligned} x \end{aligned}$ ". The entire equation above shows that $\begin{aligned} y \end{aligned}$ is a function of
::f(x) 表达式不表示乘法。它读为“ x的 f ” 。以上整个方程式显示 Y 的函数

$\begin{aligned} x : \end{aligned}$

$\begin{aligned} y = f (x) \end{aligned}$

::x: y=f( x)

Then the equation shows that this function of $\begin{aligned} x \end{aligned}$ is specifically defined as $\begin{aligned} 75 x + 250 : \end{aligned}$

$\begin{aligned} f (x) = 75 x + 250 \end{aligned}$

::然后方程显示 x 的这个函数被具体定义为 75x+250: f( x)=75x+250

This is read: " $\begin{aligned} f \end{aligned}$ of $\begin{aligned} x \end{aligned}$ is $\begin{aligned} 75 x + 250. \end{aligned}$ "
::这段文字是:"fx是75x+250"

To find the value returned by the function for an $\begin{aligned} x \end{aligned}$ -value of 7, you want to find " $\begin{aligned} f \end{aligned}$ of 7". And " $\begin{aligned} f \end{aligned}$ of 7" is "75 times 7, plus 250":

$\begin{aligned} \begin{array}{l} f (7) = 75 (7) + 250 \\ f (7) = 775 \end{array} \end{aligned}$

::要找到函数返回的值, 您想要找到“ 7 的 f ” 。而“ 7 的 f ” 是“ 75 乘 7 乘 7 + 250 ” : f(7)= 75(7)+250f(7)=775

To determine the $\begin{aligned} x \end{aligned}$ -value that returns a value of 525 for the function, you want to find $\begin{aligned} x \end{aligned}$ such that:

$\begin{aligned} 525 = f (x) \end{aligned}$

::要确定函数返回值为 525 的 x 值, 您需要找到x, 即: 525=f( x)

That is to say, 525 is a function of some value of $\begin{aligned} x . \end{aligned}$ And you know that the function $\begin{aligned} f \end{aligned}$ is defined as $\begin{aligned} 75 x + 250 : \end{aligned}$
::也就是说, 525 是某种 x 值的函数。您知道函数 f 的定义是 75x+250 :

$\begin{aligned} \begin{array}{l} 525 = 75 x + 250 \\ x = 3 \frac{2}{3} \end{array} \end{aligned}$

::525=75x+250x=323

Thus, you've shown that:
::因此,你证明了:

$\begin{aligned} f (3 \frac{2}{3}) = 525 \end{aligned}$

::f( 323) = 525

However, in the context of this scenario, Jamal cannot grow 3 and two-thirds trees! So if he doesn't want to exceed 525 dollars, he'll have to stop at 3 trees.
::但是,在这种情况下,Jamal不能种植3棵和2/3的树!所以如果他不想超过525美元,他必须停在3棵树上。

The procedure for creating the above function and using it to solve problems was no different from the methods you've used previously. The difference was in the use of function notation. Function notation is how we will frequently define functions for the remainder of this book, as it is the method most widely used throughout mathematics. Function notation allows for a much richer representation of functions, the relationships between different functions, and special characteristics of functions. You'll see more of these applications of function notation throughout your work in math in the coming years.
::创建上述函数并用它来解决问题的程序与您以前使用过的方法没有区别。区别在于使用函数符号。函数符号是我们如何经常定义本书其余部分的函数, 因为这是数学中最常用的方法。函数符号可以让功能、不同函数之间的关系和函数的特殊性有更丰富得多的表达方式。您将会在未来几年里在数学中看到更多的这些函数符号应用。

Work it Out

::工作出来

Functions can be represented with tables, equations, and graphs. Answer the questions for each function.
The equation for $\begin{aligned} f (x) \end{aligned}$ is given below. What is $\begin{aligned} f (7) ? \end{aligned}$ Find $\begin{aligned} x \end{aligned}$ such that

$\begin{aligned} f (x) = 100. \end{aligned}$

$\begin{aligned} f (x) = - \frac{3}{14} x - \frac{2}{3} \end{aligned}$

::函数可以用表格、方程和图表来表示。回答每个函数的问题。 f( x) 的方程在下面给出。 f( x) 是什么? f(7)? find x 的数值是 f( x) = 100. f( x) =314x- 23

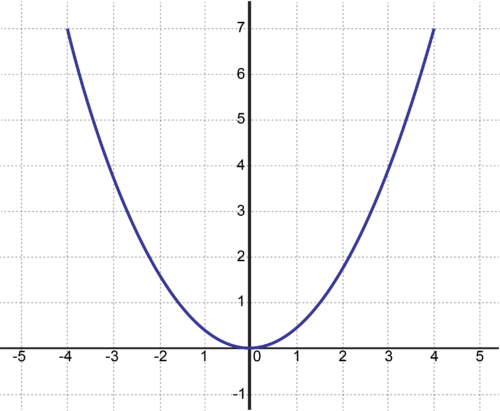
The graph of $\begin{aligned} g (x) \end{aligned}$ is shown below. What is $\begin{aligned} g (- 3) ? \end{aligned}$ Find two $\begin{aligned} x \end{aligned}$ -values such that $\begin{aligned} g (x) = 7. \end{aligned}$
::g(x) 的图形显示在下面。 g 是什么 ? 查找 2 x 值, 如 g( x) = 7 。

g(x) is a parabola

A table representing $\begin{aligned} h (x) \end{aligned}$ is shown below. What is $\begin{aligned} h (4.5) ? \end{aligned}$ Find all values of $\begin{aligned} x \end{aligned}$ such that $\begin{aligned} h (x) = 14. \end{aligned}$
::下面显示代表 h(x) 的表格。什么是 h( 4.5) ? 查找 x 的全部值, 如 h( x) = 14 。

$\begin{aligned} \begin{array}{cc} x & h (x) \\ 3 & 5 \\ 2 & 14 \\ 14 & \sqrt{2} \\ - 2 & 15 \\ 1 & 14 \\ 4.5 & 112 \\ 5.5 & 4.5 \end{array} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?

The following ordered pairs represent the relationship between $\begin{aligned} x \end{aligned}$ and $\begin{aligned} p (x) . \end{aligned}$ Each ordered pair has the form $\begin{aligned} (x, p (x)) . \end{aligned}$ What is $\begin{aligned} p (π) ? \end{aligned}$ Find all values of $\begin{aligned} x \end{aligned}$ such that $\begin{aligned} p (x) = 0. \end{aligned}$

$\begin{aligned} (9, 12) (0, - 12) (\sqrt{5}, 3) (π, 0) (\sqrt{3}, 0) (12, 0) \end{aligned}$

::下列有顺序配对代表 x 和 p( x) 之间的关系。每个有顺序配对都有表( x, p( x) ) 。 p 是什么 p ? 查找 x 的所有值, 如 p( x) = 0. ( 9, 12) (0, 10) / 12) (5, 3, (%, 0) (3, 0) (12,0)

Function Notation
::函数符号

Function notation is a method for representing a function.
::函数标记是代表函数的一种方法。

For example, if the equation for a function is $\begin{aligned} y = 5 x + 6 \end{aligned}$ , it can be represented $\begin{aligned} f (x) = 5 x + 6. \end{aligned}$
::例如,如果函数的方程式为y=5x+6,则可以代表 f(x)=5x+6。

This is read " $\begin{aligned} f \end{aligned}$ of $\begin{aligned} x \end{aligned}$ is $\begin{aligned} 5 x + 6. \end{aligned}$ " It means that $\begin{aligned} y \end{aligned}$ is a function of $\begin{aligned} x \end{aligned}$ , and the operations performed by the function are given by the expression $\begin{aligned} 5 x + 6. \end{aligned}$
::读为“ f x 是 5x+6 ” 。这意味着 y 是 x 的函数, 该函数执行的操作由表达式 5x+6 提供。

Activity 3 : Function Maps
::活动3:功能地图

Function maps are another way to represent functions.

::功能地图是代表功能的另一种方式。

Example 3-1

::例3-1

Recall Jamal and his trees from Example 2. The equation for the cost as a function of the number of trees was:
::从例2中回顾贾迈勒及其树木,根据树木数量计算成本的方程式是:

$\begin{aligned} f (x) = 75 x + 250 \end{aligned}$

:xx)=75x+250

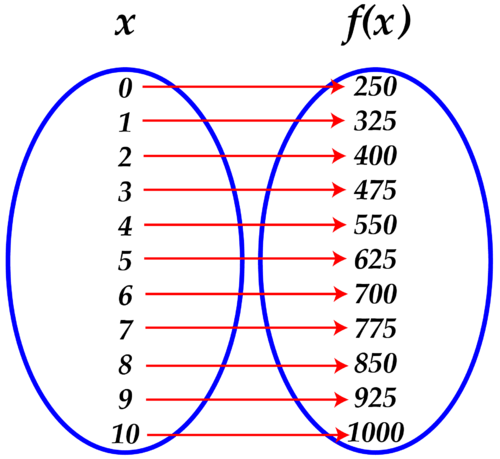
Jamal has space to grow a maximum of 10 trees. Can he grow 11 trees? Can he grow $\begin{aligned} - 3 \end{aligned}$ trees? Can he grow $\begin{aligned} 5 \frac{1}{2} \end{aligned}$ trees? Draw a vertical oval, and write all the possible $\begin{aligned} x \end{aligned}$ -values for Jamal's function in it. Draw a second oval with all the possible values for $\begin{aligned} f (x) \end{aligned}$ in it. Draw arrows from each x-value to its corresponding $\begin{aligned} y \end{aligned}$ -value. This is a function map.
::Jamal有最多10棵树的生长空间。他能种植11棵树吗? 他能种植- 3棵树吗? 他能种植512棵树吗? 他能绘制一个垂直的奥瓦尔, 并为Jamal的函数写下所有可能的 x 值。绘制一个包含 f( x) 中所有可能的值的第二个奥瓦尔。从每个 x 值中绘制箭头到相应的 y 值。这是函数映射图。

Solution:
::解决方案 :

As each value of x increases by one, each value of f(x) increases by 75, starting at x = 0 and f(x) = 250.

The above function map shows all the possible values for $\begin{aligned} x \end{aligned}$ that make sense for the given scenario. 0 is included, because although it is unlikely, Jamal could buy all the mulch and fertilizer then decide not to grow apples this year. Negative numbers don't make sense because Jamal can't grow a negative number of trees. It's also not possible to grow half of a tree--it's either a tree or it's not, and even a small tree is still one, complete tree! And Jamal can grow a maximum of 10 trees on his plot.
::上述函数映射显示 x 的所有可能值, 这对给定的情景来说是有道理的。 0 包含在其中, 因为虽然不可能, 贾马可以购买所有的木料和肥料, 然后决定今年不种植苹果。负数不合理, 因为贾马不能种植负数的树木。也不可能种植一半的树, 要么是一棵树, 要么不是一棵树, 甚至一棵小树仍然是一棵, 完整的树! 而贾马可以在他的地块上种植最多10棵树。

Example 3-2

::例3-2

The function map above shows a list of all the possible $\begin{aligned} x \end{aligned}$ -values the function can accept, given the scenario of Jamal and his trees. The map also shows all the values that $\begin{aligned} f (x) \end{aligned}$ returns, that is, all the possible costs for the different scenarios. The list of all possible $\begin{aligned} x \end{aligned}$ -values a function can accept is called the domain . The list of all the values $\begin{aligned} f (x) \end{aligned}$ can return is called the range . Suppose Jamal's friend Serena is growing orange trees. Her plot can accept a maximum of 8 trees. The cost for preparing the land is $180, and the price per tree is $45. Create the equation for the function $\begin{aligned} g (x) \end{aligned}$ to express the cost as a function of the number of trees. Represent this function using a function map. State the of the function.

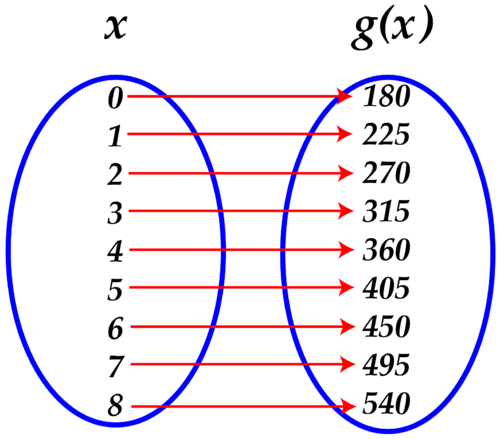
::上方的函数映射图显示函数可以接受的所有可能的 x 值列表, 考虑到 Jamal 及其树的假想情况。地图还显示 f( x) 返回的所有值, 即不同假想的所有可能成本。一个函数可以接受的所有可能的 x 值列表被命名为域。所有 f( x) 返回的值列表被命名为范围。如果Jamal 的朋友 Serena 正在种植橙色树, 她的绘图可以接受最多8 棵树。准备土地的成本是 180 美元, 每棵树的价格是 45 。创建函数 g( x) 的方程式以表达成本作为树数的函数。使用函数映射代表此函数。请描述函数的函数。

Solution: The function is: $\begin{aligned} g (x) = 45 x + 180. \end{aligned}$
::解析度: 函数为: g( x) = 45x+180 。

As each value of x increases by one, each value of g(x) increases by 45, starting at x=0 and g(x)=180.
::随着x的每个值增加1倍,g(x)的每个值增加45倍,从x=0和g(x)=180开始。

The domain and range can be represented using set notation :
::域和范围可以用设定的符号表示 :

$\begin{aligned} \begin{array}{ll} Domain: & {0, 1, 2, 3, 4, 5, 6, 7, 8} \\ Range: & {180, 225, 270, 375, 360, 405, 450, 495, 540} \end{array} \end{aligned}$

::域: {0,1,2,3,4,5,6,7,8}Range:{180,225,270,375,360,405,450,495,540}

Activity 4 : Functions and Non-functions
::活动4:职能和非职能

Example 4-1
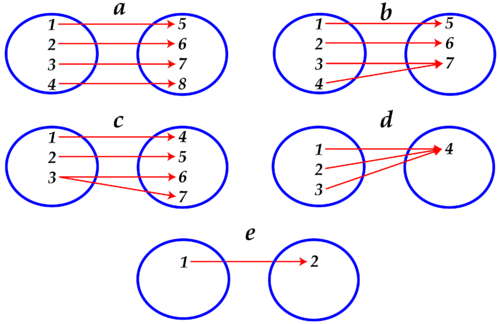
::例4-1

A function is a relation between two sets of numbers, the domain and range, such that for each element in the domain, there is only one corresponding element in the range. However, elements in the range can be "used" more than once! The function maps below show all the values for the domain and range for each relation. D etermine if each relation is a function or not. Explain your decisions.
::函数是两组数字( 域和范围)之间的关系, 因此对于域中的每一元素, 区域中只有一个相应的元素。但是, 区域中的元素可以“ 使用” 不止一次。下面的函数映射显示每个关联的域和范围的所有值。确定每个关联是否是一个函数。请解释您的决定。

Five different relations

Solution:
::解决方案 :

This is a function. For each element in the domain, there is one element in the range.
::这是一个函数。对于域中的每一元素,在范围中有一个元素。

This is a function. Although 3 and 4 in the domain both map to 7 in the range, this is still within the definition of a function.
::这是一个函数。虽然在域内有3个和4个地图,在范围中有7个地图,但这仍属于函数的定义范围。

This is not a function. 3 maps to two values in the range. A relation is only a function if each element in the domain maps to only one corresponding element in the range.
::这不是函数。 3 映射到范围中的两个值。如果域图中每个元素都与区域中一个相应的元素相匹配, 则关系只是一个函数。

This is a function. All the values in the domain map to the same value in the range, but this is still within the definition of a function.
::这是一个函数。在域图中的所有数值在范围中与数值相同,但这仍然在函数定义范围内。

This is a function. Although the domain consists of 1 value and the range of 1 value, this is still within the definition of a function.
::这是一个函数。虽然域由 1 个值和 1 个值的范围组成, 但此功能仍属于函数定义范围。

Defining a Function
::定义函数

A function is a relation between two sets of numbers, the domain and range, such that for each value in the domain, there is only one corresponding value in the range.

Work it Out
::工作出来

Katia is growing almond trees. It costs her $300 to prepare the soil and $160 per tree. She can grow a maximum of 6 trees on her plot. Create the equation for the function representing her scenario. Use function notation. Create a function map which shows the relationship between domain and range. Use set notation to represent the domain and range. Write and solve an equation to help you determine the maximum number of trees Katia can grow and still remain under $800.
::卡蒂亚正在种植杏仁树。它花费她300美元准备土壤, 每棵树160美元。她可以在自己的地块上种植最多6棵树。为代表她的情景的函数创建方程式。使用函数符号。创建显示域与范围之间关系的函数映射图。使用设置的符号代表域与范围。写入和解析一个方程式, 帮助您确定卡蒂亚可以种植的树木的最大数量, 并且仍然保持在800美元以下。

Create a map that shows a function with 3 values in the domain and 2 in the range.
::创建显示域内3个值和范围内2个值的函数的地图。

Create a map that shows a relation with 5 values in the domain and 2 in the range. Is this a function? Why or why not?
::创建地图, 显示域中5个值和范围中2个值的关系。这是函数吗? 为什么或为什么没有?

Given $\begin{aligned} q (x) = 4 x - 7 \end{aligned}$ and a domain of $\begin{aligned} {0, 1, 2, 3, 4, 5} \end{aligned}$ , create a map to represent this relation . Is this relation a function or not? Explain.
::give q(x) = 4x-7 和 {0,1、2,3,4,5} 的域, 创建显示此关系的地图。此关系是否函数? 请解释。

Given $\begin{aligned} f (x) = x^{2} \end{aligned}$ and a domain of $\begin{aligned} {- 3, - 2, - 1, 0, 1, 2, 3} \end{aligned}$ , create a map. Is this a function? Why or why not? Explain.
::给定 f( x) =x2 , 域为% 3, 2- 2, 1- 1, 0, 1, 2, 3}, 创建地图。这是函数吗? 为何不? 解释一下。

Given $\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ and a domain of $\begin{aligned} {9} \end{aligned}$ , create a map to represent this relation. Is this a function? Why or why not? Explain.

::鉴于 yx 和 {9} 的域, 请创建一个映射来代表此关系。这是函数吗? 为什么或为什么? 解释。

Summary
::摘要

We use function notation to name, represent, and work with functions.
::我们使用函数符号来命名、表示和与函数一起工作。

A function is a relation between two sets of numbers, the domain and range, such that for each value in the domain, there is only one corresponding value in the range.
::函数是两个数字组之间的关系,一个是域,另一个是区域,一个是区域,一个是区域,一个是区域,一个是区域,一个是区域,一个是区域。

PLIX Interactive
::PLIX 交互式互动

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。