Course: 3. 5 函数的反义-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

函数的逆函数

The Purpose of This Lesson
::本课程的目的

In this lesson, you will explore inverses of a given function that sometimes results in a non-function. Y ou'll develop pairs of functions that are built around inverse operations, and explore their tables, graphs, and equations. You'll apply these inverse relationships to a wider variety of functions and relations, and learn a technique for finding the equations for inverse relations.
::在此教训中, 您将探索某函数的反转, 有时导致一个功能失效。您将围绕反向操作开发一对函数, 并探索它们的表格、图表和方程。您将把这些反向关系应用到更广泛的函数和关系中, 并学习找到反向关系方程的方法。

Introduction: Composition of Functions
::导言:职能构成

Work it Out
::工作出来

For each of the following pairs of functions, f ind $\begin{aligned} f (g (x)) \end{aligned}$ and $\begin{aligned} g (f (x)) : \end{aligned}$
::对于以下各对函数,请参见 f(g(x))和 g(f(x)):

$\begin{aligned} f (x) = 3 x + 1 \end{aligned}$ and $\begin{aligned} g (x) = x^{2} \end{aligned}$
:x)=3x+1和g(x)=x2

$\begin{aligned} f (x) = 2 x + 4 \end{aligned}$ and $\begin{aligned} g (x) = \frac{1}{2} x - 2 \end{aligned}$
:xx) = 2x+4 和 g(x) = 12x-2

For part b, $\begin{aligned} f (g (x)) \end{aligned}$ and $\begin{aligned} g (f (x)) \end{aligned}$ are equal to each other, and they both equal $\begin{aligned} x, \end{aligned}$ the original input into the function. This means that there is a special relationship between these two functions. We will examine this relationship in detail later on in the lesson .
::对于b部分,f(g(x)和g(f(x))是等同的,它们都等于函数的原始输入x。这意味着这两个函数之间存在特殊关系。我们将在课后详细研究这种关系。

Activity 1 : Exploring Inverses
::活动1:探索逆数

Example 1-1
::例1-1

Make a table and graph for the function $\begin{aligned} y = x^{2} . \end{aligned}$ Consider the equation $\begin{aligned} y^{2} = x . \end{aligned}$ Solve it for $\begin{aligned} y \end{aligned}$ . Create a table and graph. Compare the tables and graphs of both equations. Which is a function and which isn't? Compare the domain and range of both.
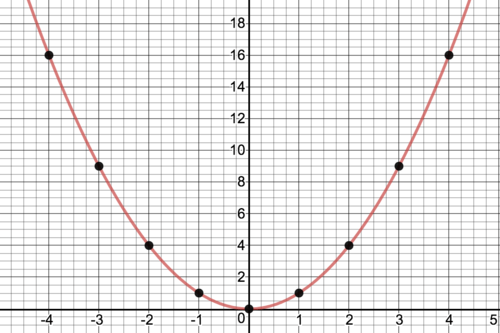
::为 y=x2 函数制作表格和图表。考虑公式 y2=x。为 y 解决它。创建表格和图表。比较两个方程式的表格和图表。哪一个是函数, 哪一个不是? 比较两个方程式的域和范围。

Solution: The function $\begin{aligned} y = x^{2} \end{aligned}$ is quadratic. The table and graph are below:
::解析度 : 函数 y=x2 是二次曲线。表格和图表如下 :

\begin{aligned} \begin{array}{cc} x & y \\ - 4 & 16 \\ 4 & 16 \\ - 3 & 9 \\ 3 & 9 \\ - 2 & 4 \\ 2 & 4 \\ - 1 & 1 \\ 1 & 1 \\ 0 & 0 \end{array} \end{aligned}

::xy-416416-3939-2424-111100

The graph of the data in the table. The shape is a parabola.
::表格中的数据图表。形状是抛物线。

The equation $\begin{aligned} y^{2} = x \end{aligned}$ is the same as $\begin{aligned} y = x^{2}, \end{aligned}$ except $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ are reversed. If you solve $\begin{aligned} y^{2} = x \end{aligned}$ for $\begin{aligned} y \end{aligned}$ you get:
::y2=x 等式与 y=x2 相同, 但 x 和 y 被反转。如果您为 y 解析 y2=x , 得到 :

\begin{aligned} y = \pm \sqrt{x} \end{aligned}

::yx

The resulting table reverses the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ -values from the table for $\begin{aligned} y = x^{2} : \end{aligned}$
::结果的表格将x和y值从 y=x2 的表格中反转过来:

\begin{aligned} \begin{array}{cc} x & y \\ 16 & 4 \\ 16 & - 4 \\ 9 & 3 \\ 9 & - 3 \\ 4 & 2 \\ 4 & - 2 \\ 1 & 1 \\ 1 & - 1 \\ 0 & 0 \end{array} \end{aligned}

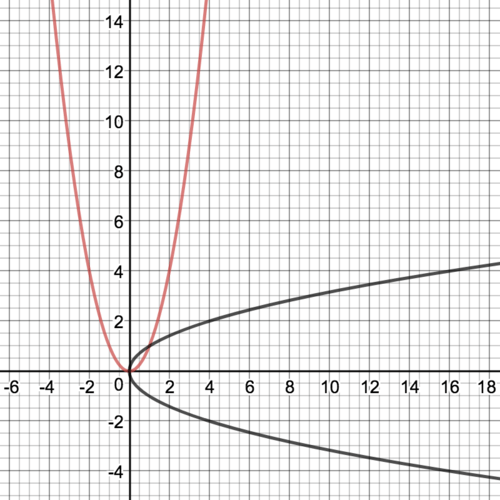
::xy16416-4939-3424-2111-100

The graph of both $\begin{aligned} y = x^{2} \end{aligned}$ and $\begin{aligned} x = y^{2} \end{aligned}$ are shown below. Both the table and graph show that $\begin{aligned} x = y^{2} \end{aligned}$ is not a function.
::Baty=x2和x=y2的图示如下。表格和图示都显示 x=y2 不是一个函数。

One 'up' parabola, and one 'sideways' parabola. Only one is a function.
::一种“ 上” 抛物线, 一种“ 侧面” 抛物线。只有一种是函数。

Here are the domain and range for each:
::以下是每个域的域和范围 :

$\begin{aligned} \begin{array}{lcc} y = x^{2} & x = y^{2} \\ Domain & (- \infty, \infty) & [0, \infty) \\ Range & [0, \infty) & (- \infty, \infty) \end{array} \end{aligned}$

::y=x2x=y2Domain(,) [0,]Range[0,]()(,))

Just as $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ reversed positions in the tables, the domain and range are reversed.
::正如表格中的 x 和 y 的反向位置一样,域和范围被反向。

Finally, note that the equation $\begin{aligned} y = x^{2} \end{aligned}$ involves squaring, while $\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ involves square rooting. These are inverse operations. $\begin{aligned} y = x^{2} \end{aligned}$ and $\begin{aligned} x = y^{2} \end{aligned}$ are inverses of each other.
::最后,请注意,y=x2的方程涉及方程,y=x涉及平方根。这些是反向操作。y=x2和x=y2是彼此的反向操作。

Inverse Relations
::反反关系

Table representations of inverse relationships show reversed $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ -values.
::反向关系表显示反向 x 和 Y 值。

The inverse of a function might be a non-function.
::职能的反向可能是非职能。

The domain and range of inverse relations are reversed.
::反向关系的领域和范围被逆转。

The equations of inverse relations show inverse operations.
::反向关系方程式显示反向操作。

Work it Out
::工作出来

Create the table and graph for the two equations here. Give their domain and range. Are they both functions? Are they inverses of each other? Explain.
::在此创建两个方程式的表格和图表。给出它们的域和范围。它们是否都具有函数? 它们是否互相反向? 解释。

\begin{aligned} \begin{array}{l} y = 2 x + 3 \\ x = 2 y + 3 \end{array} \end{aligned}

::y=2x+3x=2y+3 y

Interactive
::交互式互动

Using the interactive below, discuss whether the original and the inverse of each are functions. Approximate one point on each original, then confirm that the corresponding "reversed" point is on the inverse. Give the domain and range of each original and inverse.
::使用下面的交互效果, 讨论每个函数的原始和反正是否是函数。每一个原始的大约一点, 然后确认对应的“ 反向” 点在反向点上。给出每个原始和反向的域和范围。

Activity 2: Functions for Inverse Operations
::活动2:反反向业务的职能

Example 2-1
::例2-1

Consider the function $\begin{aligned} f (x) = 2 x . \end{aligned}$ The point (5, 10) is on the graph of this function.
::考虑函数 f( x) = 2x。点 (5, 10) 位于此函数的图形上。

What mathematical operation does this function perform on $\begin{aligned} x ? \end{aligned}$ What mathematical operation would reverse this operation?
::这个函数在 x 上执行什么数学操作? 什么数学操作会逆转这个操作 ?

The function $\begin{aligned} f (x) \end{aligned}$ transforms a 5 into a 10. What function would reverse that transformation? Call this function $\begin{aligned} g (x) . \end{aligned}$
::函数 f( x) 将 5 转换为 10. 。哪个函数可以逆转这种转换? 调用此函数 g( x) 。

Use function maps to show the relationship between $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) . \end{aligned}$
::使用函数映射显示 f( x) 和 g( x) 之间的关系。

What is $\begin{aligned} g (f (x)) ? \end{aligned}$ What is $\begin{aligned} f (g (x)) ? \end{aligned}$ Interpret this result in the context of your observations above.
::g(f(x)是什么?f(g(x))是什么?f(g(x))是什么?结合上述意见解释这一结果。

Solution: The function $\begin{aligned} f (x) = 2 x \end{aligned}$ multiplies $\begin{aligned} x \end{aligned}$ -values by 2. The inverse operation of multiplying by 2 is multiplying by $\begin{aligned} \frac{1}{2} . \end{aligned}$ The function built from this inverse operation is $\begin{aligned} g (x) = \frac{1}{2} x . \end{aligned}$
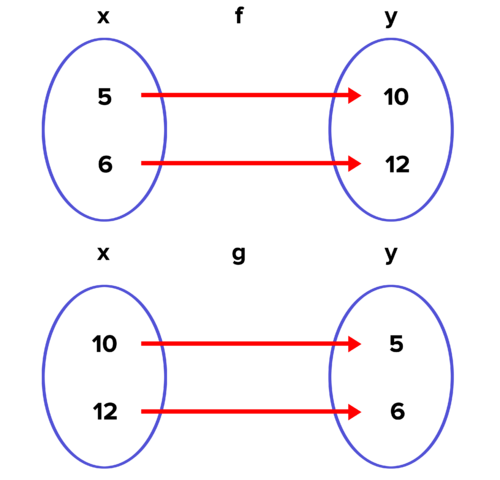
::解析度: 函数 f( x) = 2x 乘以 x- 值乘以 2. 乘以 2 的反函数乘以 12 。从此反函数创建的函数为 g( x) = 12x 。

The function map shows that x and y exchange positions.
::函数映射显示 x 和 y 交换位置。

The following table shows the general results when we create a composite of $\begin{aligned} f (x) = 2 x \end{aligned}$ and $\begin{aligned} g (x) = \frac{1}{2} x : \end{aligned}$
::下表显示当我们创建 f( x) = 2x 和 g( x) = 12x 组合时的总结果:

$\begin{aligned} \begin{array}{lll} First Composite & Second Composite & Explanation \\ g (f (x)) & f (g (x)) & Composite functions. \\ g (2 x) & f (\frac{1}{2} x) & Substituting. \\ \frac{1}{2} (2 x) & 2 (\frac{1}{2} x) & Evaluating. \\ x & x & Simplifying. \end{array} \end{aligned}$

::首个复合二合成排除g(f(x))f(g(x)x)复合函数。 g(2x)f(12x)替代12(2x)(12x)Evaluation.xxSimplication。

This is consistent with the relationship shown in the function map. Suppose 5 is substituted for $\begin{aligned} x \end{aligned}$ in $\begin{aligned} f . \end{aligned}$ The result is 10. If 10 is then substituted for $\begin{aligned} x \end{aligned}$ in $\begin{aligned} g, \end{aligned}$ 5 is returned. In general, each function reverses the operations of the other. These functions are inverses of each other.
::这与函数映射中显示的关系是一致的。假設 5 取代 f 中的 x。结果为 10 。如果 10 替换 x g 中的 x, 则返回 5 。一般来说, 每一个函数会反转对方的操作。这些函数是反向的。

Inverse Linear Functions
::反直线函数

Two linear functions $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are inverses if one reverses the operations of the other.
::两个线性函数 f(x) 和 g(x) 如果反向另一个函数的操作, 则反向为 f(x) 和 g(x) 。

Specifically, $\begin{aligned} g (f (x)) = x \end{aligned}$ and $\begin{aligned} f (g (x)) = x . \end{aligned}$
::具体而言, g(f(x))=x和f(g(x))=x。

If $\begin{aligned} (a, b) \end{aligned}$ is a solution of $\begin{aligned} f (x), \end{aligned}$ then $\begin{aligned} (b, a) \end{aligned}$ a solution of $\begin{aligned} g (x) . \end{aligned}$
::如果(a,b)是f(x)的解决方案,那么(b,a)是g(x)的解决方案。

Interactive
::交互式互动

Use the interactive below to explore the relationship between the graphs of a linear function and its inverse and discuss the questions below. The given function is shown, with a point on the graph, and a rectangle representing the coordinates of the point. Adjust the parameters of the given function and point with the slider.
::使用下面的交互作用来探索线性函数的图形与其反向关系,并讨论下面的问题。显示给定的函数,在图形上加上一个点,以及代表点坐标的矩形。调整给定函数和点的参数与滑动符。

Anticipate the location of the corresponding point on the inverse. Anticipate the graph and equation for the inverse. Then click the checkbox to see if you were correct. Repeat the exercise with different points and functions.
::预测反向对应点的位置。预测反向的图形和方程式。然后单击复选框查看您是否正确。用不同的点和函数重复练习。

Why do both functions intersect the point (0,0)? How do the point and its corresponding location on the graph of the inverse relate to the dotted line graphed, $\begin{aligned} y = x ? \end{aligned}$ Explain.
::为何两个函数都交叉点( 0,0) ? 反向图中点及其相应位置与虚线图解的 y=x 有关? 解释。

How do the graphs of the function and its inverse relate to each other and the line $\begin{aligned} y = x ? \end{aligned}$ Explain.
::函数的图形及其反向与 y=x 和 y=x 线条的关系如何? 解释。

Is it possible to create a function whose inverse is identical to the original function? Explain.
::是否有可能创建一个函数, 其反向与原始函数相同? 解释。

Interactive
::交互式互动

Repeat the above investigation with the additional parameter of a non-zero $\begin{aligned} y \end{aligned}$ -intercept.
::重复上述调查,加上非零 Y 界面的附加参数。

Interactive
::交互式互动

Use the interactive to explore the impact of exchanging the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values of each vertex of a polygon. Record your observations. How does the relationship between these two polygons reflect the relationship between a function and its inverse?
::使用互动来探索多边形每个顶点的 x 和 Y 值交换的影响。记录您的观察。这两个多边形之间的关系如何反映函数与其反向之间的关系 ?

Graphs of Inverses
::逆数图

If $\begin{aligned} (a, b) \end{aligned}$ is on the graph of a function, then $\begin{aligned} (b, a) \end{aligned}$ is on the graph of its inverse.
::如果(a,b)在函数图中,(b,a)在其反向图中。

The graph of a function and its inverse are reflections of each other across the line $\begin{aligned} y = x . \end{aligned}$
::函数图及其反向是横跨 y=x 线的反射。

Work it Out
::工作出来

Given the function $\begin{aligned} f (x) = 2 x + 3. \end{aligned}$ What operations does this function perform on a given value of $\begin{aligned} x ? \end{aligned}$ Describe them in order. What operations, in what , would reverse the operations performed by $\begin{aligned} f (x) ? \end{aligned}$ Therefore, what is the inverse function of $\begin{aligned} f (x) ? \end{aligned}$ Call it $\begin{aligned} g (x) . \end{aligned}$ Find each of the following to confirm that $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are inverses. Explain how each result confirms that to be the case.
::鉴于函数 f( x) = 2x+3. , 此函数在 x 的给定值上执行什么操作? 按顺序描述它们。什么样的操作会逆转 f( x) 执行的操作? 因此, f( x) 的反作用是什么? 调用 g( x) 。查找以下每个函数以确认 f( x) 和 g( x) 是反的。解释每个结果如何确认为属于这种情况。

$\begin{aligned} \begin{array}{ll} a. & f (8) \\ b. & g (f (8)) \\ c. & g (- 5) \\ d. & f (g (- 5)) \\ e. & g (f (x)) \\ f. & f (g (x)) \end{array} \end{aligned}$
:f)(8)b.g(f(8))c.g(-5)d.f(g(-5))e.f(f(x))f.f(g(x))

Activity 3 : Finding the Equation for the Inverse of a Given Function
::活动3:为存在功能的反向寻找公式

Example 3-1
::例3-1

In the last problem, you created an inverse function by reversing the operations of a given function, in reverse order. Similarly, every time we solve equations involving a given function, you reverse the operations in reverse order. Consider the equation $\begin{aligned} 17 = 3 x + 5 : \end{aligned}$
::在最后一个问题中,您创建了反向函数,以反向顺序逆转给定函数的运行。同样,每当我们解决涉及给定函数的方程式时,您按反向顺序将操作反向。考虑公式 17=3x+5 :

\begin{aligned} \begin{array}{ll} Equation & Explanation \\ f (x) = 3 x + 5 & The given function multiplies by 3 then adds 5. \\ 17 = 3 x + 5 & Given equation. \\ 17 - 5 = 3 x & Subtracting 5. \\ \frac{17 - 5}{3} = x & Dividing by 3. \\ x = 4 & Simplifying. \end{array} \end{aligned}

::EquationExplainationf(x)=3x+5 给定函数乘以 3 3, 然后添加5. 17= 3x+ 5Fendern 等式 17 - 5= 3x 减法 5. 17 - 53=x divide 乘以 3. x= 4Simplication 。

Because solving an equation requires the use of the inverse operations in the reverse order, the same process can be used to find the equation for an inverse. In the above example, you applied those inverse operations in the reverse order to the number 17. To build an inverse, you want to apply those same operations to a variable. What variable? Previously you observed that if a point $\begin{aligned} (a, b) \end{aligned}$ is on the graph of a function, then the point $\begin{aligned} (b, a) \end{aligned}$ is on the graph of the inverse. Exchange $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ in the equation $\begin{aligned} y = 3 x + 5, \end{aligned}$ then use inverse operations to solve for $\begin{aligned} y . \end{aligned}$ Confirm the resulting function is the inverse of the original by evaluating $\begin{aligned} g (f (x)) \end{aligned}$ and $\begin{aligned} f (g (x)) . \end{aligned}$
::由于解答一个方程需要使用反向操作的反向顺序, 也可以使用相同的进程来查找反向的方程。在上述示例中, 您在反向顺序中应用了反向操作到数字 17 。要建立反向, 您想要将同样的操作应用到变量中。是什么变量? ? 之前您观察到, 如果一个函数的图形上有一个点( a, b) , 那么, 点( b, a) 在反向图中。在 y=3x+5 中, 交换 x 和 y , 然后使用反向操作来为 y. 通过评价 g( f( x) ) 和 f( g( x) ) 来确认所产生的函数是原函数的反向值。

Solution:
::解决方案 :

\begin{aligned} \begin{array}{ll} Equation & Explanation \\ f (x) = 3 x + 5 & Original function using function notation. \\ y = 3 x + 5 & Original function. \\ x = 3 y + 5 & Equation representing the inverse. \\ x - 5 = 3 y & Reversing operations. \\ \frac{x - 5}{3} = y & Reversing operations. \\ y = \frac{1}{3} x - 1 \frac{2}{3} & Simplifying. \\ g (x) = \frac{1}{3} x - 1 \frac{2}{3} & Writing using function notation. \end{array} \end{aligned}

::equationExplainationf(x)=3x+5 原件功能,使用函数符号 y= 3x+5 原件函数。x= 3y+5 表示反向.x-5= 3yRevering 操作。x= 53= y= 13x-123Simpligiation.g(x)=13x-123

\begin{aligned} \begin{array}{ll} First Composite & Second Composite \\ g (f (x)) & f (g (x)) \\ g (3 x + 5) & f (\frac{1}{3} x - 1 \frac{2}{3}) \\ \frac{1}{3} (3 x + 5) - 1 \frac{2}{3} & 3 (\frac{1}{3} x - 1 \frac{2}{3}) + 5 \\ x + \frac{5}{3} - 1 \frac{2}{3} & x - 5 + 5 \\ x & x \end{array} \end{aligned}

::第一次复合(f(x))f(g(x))g(3x+5)g(3x+5)f(13x-123)13(3x+5)-123(13x+5)-1233(13x-123)+5x+53-123x-5+5xx

Work it Out
::工作出来

Find the inverse function for each of the following. Call it $\begin{aligned} g (x) . \end{aligned}$ Confirm they are inverses by substituting values, graphing, or evaluating $\begin{aligned} g (f (x)) \end{aligned}$ or $\begin{aligned} f (g (x)) . \end{aligned}$
::查找以下每一种的反函数。调用 g(x) 。确认它们为反函数, 替换值、图形化或评价 g(f(x) ) 或 f(g(x) ) 。

$\begin{aligned} \begin{array}{ll} a. & f (x) = 4 x - 1 \\ b. & f (x) = \frac{1}{2} x \\ c. & f (x) = - \frac{2}{3} x - 7 \\ d. & f (x) = x \\ e. & f (x) = - x \\ f. & f (x) = x^{3} \end{array} \end{aligned}$
::af( x) = 4x- 1b.f( x) = 12xc. f( x) = 23x- 7d. f( x) = xe. f( x) x* xf. f( x) =x3

Finding the Equation for the Inverse of a Linear Function
::查找线性函数反向的公式

The inverse of a linear function performs the inverse operations of the original in the reverse order.
::线性函数的反向函数以反向顺序执行原始函数的反向操作。

Its equation can be found by the following procedure:
::其等式可通过以下程序找到:

Exchange $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ in the equation.
::在方程式中交换 x 和 y 。

Solve for $\begin{aligned} y . \end{aligned}$
::解决你。

Activity 4 : Inverses for Other Relations
::活动4:其他关系逆数

To this point, you've explored inverses of linear functions. However, linear equations aren't the only kind with inverses. The inverse of any equation can be found with the right process.
::到此点, 您已经探索了线性函数的反向。然而, 线性方程式并不是唯一带有反向的方程式。任何方程式的反向都可以通过正确的进程找到。

Recall that t he graph of a circle with radius $\begin{aligned} r \end{aligned}$ and center at the origin is given by the equation: $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$
::回顾以半径 r 和中点为原点的圆圆的图形是由公式: x2+y2=r2 给出的

The graph of a circle with radius r and center at the point $\begin{aligned} (h, k) \end{aligned}$ is given by the equation: $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$
::以(h,k) 点为圆半径(r) 和中点(h,k) 的圆形图由方程式给出x-h) 2+(y-k) 2=r2

Example 4-1
::例4-1

Graph the circle given below. Substitute values for $\begin{aligned} x \end{aligned}$ or $\begin{aligned} y \end{aligned}$ in order to get points on your graph. As you did previously, exchange the variables $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ to create the equation for the inverse. You can re-arrange this equation slightly so it's in standard form for a circle, but do not solve for $\begin{aligned} y . \end{aligned}$ Graph the resulting circle and compare it to the original. Graph the line $\begin{aligned} y = x . \end{aligned}$ What do you observe?
::绘制下面给出的圆。 x 或 y 的替代值,以便获得您的图表上的点。和以前一样,交换变量 x 和 y 来创建反方程。您可以略微重新排列此方程式,使其以标准格式对一个圆进行排列,但对于y 则不解答。绘制所生成的圆,并将其与原始的圆进行比较。绘制行 y=x 。您观察了什么?

\begin{aligned} (x - 3)^{2} + (y - 5)^{2} = 25 \end{aligned}

x-3)2+(y-5)2=25

Solution: By exchanging $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ in the equation, we see that the equation for the inverse is $\begin{aligned} (y - 3)^{2} + (x - 5)^{2} = 25, \end{aligned}$ which is $\begin{aligned} (x - 5)^{2} + (y - 3)^{2} = 25. \end{aligned}$ in standard form for a circle.
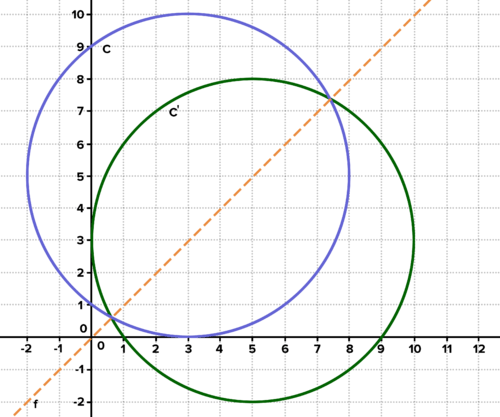
::解答:通过在方程式中交换 x 和 y,我们看到反方方程式为(y-3)2+(x-5)2=25,即(x-5)2+(y-3)2=25。

The graph of the original circle and its inverse are shown below. The inverse is the reflection of the original across the line $\begin{aligned} y = x . \end{aligned}$
::原始圆图及其反向显示在下面。反之,是原始横跨Y=x线的反射。

Interactive
::交互式互动

Use the following interactive to explore the relationship between a circle and its inverse. Record your observations.
::使用以下互动方式来探索圆及其反向之间的关系。记录您的意见。

Remember this!

The inverse of a function is one that reverses the operations of the original function.
::函数的反向值是反向原始函数运行的函数。

Two linear functions $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ are inverses if $\begin{aligned} g (f (x)) = x \end{aligned}$ and $\begin{aligned} f (g (x)) = x . \end{aligned}$
::如果 g(f(x)) =x 和 f(g(x)) =x =x,则两个线性函数 f(x) 和 g(x) =x 则为反函数。

The graph of a function and its inverse are reflections of each other across the line $\begin{aligned} y = x . \end{aligned}$
::函数图及其反向是横跨 y=x 线的反射。

To find the inverse of a linear function, switch the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ variables in the equation, then solve for $\begin{aligned} y . \end{aligned}$
::要找到线性函数的反向, 请在方程式中切换 x 和 y 变量, 然后为 y 求解。

Section outline

General

函数的逆函数

The Purpose of This Lesson ::本课程的目的

Introduction: Composition of Functions ::导言:职能构成

Work it Out ::工作出来

Activity 1 : Exploring Inverses ::活动1:探索逆数

Example 1-1 ::例1-1

Inverse Relations ::反反关系

Work it Out ::工作出来

Interactive ::交互式互动

Activity 2: Functions for Inverse Operations ::活动2:反反向业务的职能

Example 2-1 ::例2-1

Inverse Linear Functions ::反直线函数

Interactive ::交互式互动

Interactive ::交互式互动

Interactive ::交互式互动

Graphs of Inverses ::逆数图

Work it Out ::工作出来

Activity 3 : Finding the Equation for the Inverse of a Given Function ::活动3:为存在功能的反向寻找公式

Example 3-1 ::例3-1

Work it Out ::工作出来

Finding the Equation for the Inverse of a Linear Function ::查找线性函数反向的公式

Activity 4 : Inverses for Other Relations ::活动4:其他关系逆数

Example 4-1 ::例4-1

Interactive ::交互式互动

The Purpose of This Lesson
::本课程的目的

Introduction: Composition of Functions
::导言:职能构成

Work it Out
::工作出来

Activity 1 : Exploring Inverses
::活动1:探索逆数

Example 1-1
::例1-1

Inverse Relations
::反反关系

Work it Out
::工作出来

Interactive
::交互式互动

Activity 2: Functions for Inverse Operations
::活动2:反反向业务的职能

Example 2-1
::例2-1

Inverse Linear Functions
::反直线函数

Interactive
::交互式互动

Interactive
::交互式互动

Interactive
::交互式互动

Graphs of Inverses
::逆数图

Work it Out
::工作出来

Activity 3 : Finding the Equation for the Inverse of a Given Function
::活动3:为存在功能的反向寻找公式

Example 3-1
::例3-1

Work it Out
::工作出来

Finding the Equation for the Inverse of a Linear Function
::查找线性函数反向的公式

Activity 4 : Inverses for Other Relations
::活动4:其他关系逆数

Example 4-1
::例4-1

Interactive
::交互式互动