Course: 3.11 二次曲线函数的垂直形态-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

二次曲线函数的垂直形态

The Purpose of this Lesson
::本课程的目的

In this lesson, you will expand on your work with transformations of functions by introducing vertical stretches . You'll use this context to explore and define vertex form for a quadratic function .
::在此课中, 您将会通过引入垂直伸展来扩展您在函数转换方面的工作。您将使用此上下文来探索和定义二次函数的顶点形式。

Introduction: Vertical and Horizontal Shifts of Functions
::导言:职能的纵向和横向转移

Work it Out
::工作出来

Previously, you may have performed vertical and horizontal shifts of given functions. Below are several functions. Apply the stated translations to the function . Write the equation for the function resulting from translation of the original.
::以前,您可能已经执行过给定函数的垂直和水平转移。以下是几个函数。对函数应用指定的翻译。写出因翻译原件而产生的函数的方程式。

$\begin{aligned} \begin{array}{llcc} Function & Vertical Shift & Horizontal Shift \\ a. & f (x) = x^{2} & 3 & 7 \\ b. & g (x) = | x | & - 5 & 2 \\ c. & h (x) = \sqrt{x} & - 6 & - 1 \\ d. & y = - 5 x^{2} & 0 & 8 \\ e. & y = \frac{6}{x} & 9 & - 7 \\ f. & y = f (x) & 4 & 1 \\ g. & y = e^{x} & 1 & 0 \\ h. & a_{n} = a_{1} (2)^{x - 1} & 3 & - 4 \end{array} \end{aligned}$
::函数Vertical ShiftHortical Shifta.f(x) =x237b.g(x) x x 52c.h(x) =x-6-1-dd.y5x208e.y=6x9-7f.y=f(x)41g.y=ex10h.an=a1(2)x-13-4

Give the vertex for each of the following translated quadratic and absolute value functions. Give the domain and range for each. Sketch a graph if necessary to support your conclusions.
::给以下被翻译的二次函数和绝对值函数的顶点。给每个函数提供域和范围。如有必要,请绘制一个图表来支持你的结论。

$\begin{aligned} \begin{array}{ll} a. & f (x) = x^{2} + 7 \\ b. & g (x) = | x - 1 | \\ c. & h (x) = | x + 5 | - 10 \\ d. & f (x) = 3 (x - 5)^{2} - 10 \\ e. & g (x) = 4 x^{2} - 11 \\ f. & y = - 5 (x + 7)^{2} \end{array} \end{aligned}$
::a.f(x) =x2+7b.g(x) =x2+7b.g(x) =x* *x -1* *c.h(x) =x+5* =10d.f(x) =3(x-5) 2 -10e.例如(x) =4x2-11f.y=5(x+7)2

Activity 1: Vertical Stretches
::活动1:垂直伸展

Example 1-1
::例1-1

Given below are three quadratic functions of the form $\begin{aligned} y = a x^{2} . \end{aligned}$ Complete the tables for each, and graph each on the same axes. Find the differences between consecutive values in the tables. Represent this on the graphs of each with example triangles. What do these differences and slope triangles represent? How does this confirm what you already know about quadratic functions and the scenarios they model? Return to the tables and find the differences between the differences you found. What does this value represent? Explain in the context of the equation for each function and what you already know about quadratic functions. How do the $\begin{aligned} y \end{aligned}$ -values change as the value for $\begin{aligned} a \end{aligned}$ changes? Explain.
::下面给出的是表y=ax2的三个二次函数。完成每个表格的表格, 并在同一轴上绘制每个图表。查找表格中连续值的差异。以示例三角在每个图表中代表这个数值。这些差异和斜度三角代表什么? 这如何证实您已经知道的二次函数及其模型情景? 回到表格中, 并找到您发现的差异之间的差别。这个值代表什么? 在每个函数的方程中解释每个函数的方程以及您已经知道的二次函数。 Y 值如何变化作为变化的值? 解释。

\begin{aligned} \begin{array}{cc} x & f (x) = \frac{1}{3} x^{2} \\ - 5 \\ - 4 \\ - 3 \\ - 2 \\ - 1 \\ 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array} \end{aligned}

\begin{aligned} \begin{array}{cc} x & f (x) = x^{2} \\ - 5 \\ - 4 \\ - 3 \\ - 2 \\ - 1 \\ 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array} \end{aligned}

\begin{aligned} \begin{array}{cc} x & f (x) = 2 x^{2} \\ - 5 \\ - 4 \\ - 3 \\ - 2 \\ - 1 \\ 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array} \end{aligned}

Solution: Use the interactive below to help you see how changing $\begin{aligned} a \end{aligned}$ affects the graph and table .
::解决方案: 使用下面的交互式数据来帮助您了解一个变化如何影响图形和表格。

The tables show the differences between consecutive $\begin{aligned} y \end{aligned}$ -values increase at a constant rate .
::表格以恒定速率显示连续的y值增长之间的差额。

This makes sense because the quadratic is commonly used to model objects that are subject to a constant acceleration, and a constant acceleration means that the slope increases at a constant rate.
::这样做是有道理的,因为四方形通常用于模拟受恒定加速度影响的物体,而恒定加速度意味着坡度以恒定速度上升。

Notice that in all cases, the slopes are negative to the left of $\begin{aligned} x = 0, \end{aligned}$ and steadily increase until they are positive, then continue increasing.
::请注意,在所有情况下,斜坡向x=0左边为负值,在正值之前稳步上升,然后继续上升。

The rate of increase of the slope is given by the second difference . This value represents the rate of acceleration for each function.
::斜坡的增长率以第二个差数表示,该值代表每个函数的加速率。

The rate of acceleration for a quadratic function with $\begin{aligned} a = 1 \end{aligned}$ is 2.
::a=1的二次函数加速率为2。

This makes sense because you halve the acceleration to create a quadratic model for an accelerating object. For example, if an object is accelerating at 10 meters per second, per second, the function is $\begin{aligned} y = 5 x^{2} . \end{aligned}$ Given the function $\begin{aligned} y = 5 x^{2}, \end{aligned}$ double the coefficient of 5 to find the acceleration of 10 meters per second per second.
::这之所以有意义,是因为您将加速度减半,以创建加速物体的二次模型。例如,如果一个物体加速速度为每秒10米,每秒10米,则函数为y=5x2。根据y=5x2的函数,5倍于5的系数,以发现加速速度为每秒10米。

The rate of acceleration for $\begin{aligned} y = \frac{1}{3} x^{2} \end{aligned}$ is $\begin{aligned} \frac{2}{3} . \end{aligned}$ This is confirmed by using the method described above as well as by looking at the second differences in the table. The second differences show that the slope, i.e., the speed , is increasing at a constant rate of $\begin{aligned} \frac{2}{3} . \end{aligned}$
::y=13x2的加速率是23, 使用上述方法并通过查看表中的第二个差异来证实这一点。第二个差异显示,斜坡,即速度,正以23的恒定速率增长。

The rate of acceleration for $\begin{aligned} y = 2 x^{2} \end{aligned}$ is 4. This can be calculated by doubling the coefficient of 2, or by looking at the second differences in the table: 4.
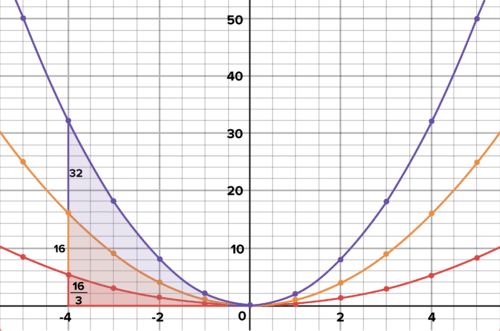
::y=2x2加速率为4。计算方法是将系数2翻一番,或查看表中的第二个差异:4。

Compare the values returned by each function for $\begin{aligned} x = - 4. \end{aligned}$
::比较 x4 中每个函数返回的数值。

When $\begin{aligned} a = 1, \end{aligned}$ the quadratic returns 16 for $\begin{aligned} x = - 4. \end{aligned}$
::a=1 时, x% 4 的二次曲线返回 16 。

When $\begin{aligned} a = 2, \end{aligned}$ the quadratic returns 32. That's twice 16.
::当 a=2, 二次方位返回32, 即是2 16 。

When $\begin{aligned} a = \frac{1}{3}, \end{aligned}$ the quadratic returns $\begin{aligned} \frac{16}{3} . \end{aligned}$ That's one-third of 16.
::a=13时, 二次方返回163。这是 16 的三分之一。

The $\begin{aligned} y \end{aligned}$ -values returned by $\begin{aligned} y = a x^{2} \end{aligned}$ are the values returned by $\begin{aligned} y = x^{2}, \end{aligned}$ multiplied by $\begin{aligned} a . \end{aligned}$
::Y=ax2返回的y值是y=x2返回的y值乘以a。

Changing the Leading Coefficient in a Quadratic Function

::在 Quadratic 函数中更改领导系数

The leading coefficient of a quadratic function is the coefficient of the quadratic term .
::二次函数的主要系数是二次函数的系数。

Given $\begin{aligned} y = a x^{2} + b x + c, \end{aligned}$ the leading coefficient is $\begin{aligned} a . \end{aligned}$
::鉴于y=ax2+bx+c,主要系数为a。

Compared with $\begin{aligned} y = x^{2}, \end{aligned}$ the $\begin{aligned} y \end{aligned}$ -values for $\begin{aligned} y = a x^{2} \end{aligned}$ are multiplied by $\begin{aligned} a \end{aligned}$ .
::与 y=x2 相比, y= ox2 的 Y 值乘以 a。

This stretches $\begin{aligned} (a > 1) \end{aligned}$ or shrinks $\begin{aligned} (0 < a < 1) \end{aligned}$ the graph vertically .
::此平面( a>1) 或缩小( 0 < a<1) 垂直的图形。

The rate of acceleration for the quadratic model is twice the coefficient of the leading term.
::二次模型的加速率是前一学期系数的两倍。

It's visible as the second difference in the table.
::这是表上的第二个差异

PLIX Interactive
::PLIX 交互式互动

Activity 2: Changing the Leading Coefficient in a Quadratic Function
::活动2:在二次曲线函数中改变领导系数

Interactive
::交互式互动

Use the following interactive to explore the impact of changing the leading coefficient of a quadratic function. Explain why a negative leading coefficient means the graph opens downward. If $\begin{aligned} a < 0, \end{aligned}$ what is the range for $\begin{aligned} y = a x^{2} ? \end{aligned}$ Explain.
::使用以下互动来探索改变二次函数主要系数的影响。解释为什么负主要系数意味着图形向下打开。如果是 < 0, y=ax2 的范围是多少? 解释。

Interactive
::交互式互动

Use the interactive to explore the impact of changing the shown parameters for the quadratic. Write the equations for several of the functions you create, and give the vertex and range. Explain the relationship between the vertex and range, and the parameters.
::使用该互动来探索改变二次参数所显示参数的影响。写入您创建的若干函数的方程, 并给出顶点和范围。解释顶点和范围之间的关系, 以及参数。

Vertex Form for a Quadratic Function
::二次曲线函数的螺旋格式

$\begin{aligned} y = a (x - h)^{2} + k \end{aligned}$
::y=a(x-h)2+k

This is a vertical stretch of $\begin{aligned} y = x^{2} \end{aligned}$ by a factor of $\begin{aligned} a . \end{aligned}$
::这是 Y=x2 乘以 a 的垂直伸展。

The vertex is $\begin{aligned} (h, k) . \end{aligned}$
::顶点是 (h,k) 。

Work it Out
::工作出来

Explain the difference between each of the following functions and $\begin{aligned} y = x^{2} . \end{aligned}$ Specifically, describe the nature of the stretch or shrink, how it impacts $\begin{aligned} y \end{aligned}$ -values, and the rate of acceleration of the quadratic. Explain how this relates to the rate of increase in the steepness of the graph.
::解释以下函数与 y=x2 之间的差别。具体地说, 描述伸展或缩缩的性质, 如何影响 y 值, 以及二次曲线的加速度。解释这与图形陡峭度的增长率有何关系。

$\begin{aligned} \begin{array}{ll} a. & f (x) = 3 x^{2} \\ b. & g (x) = \frac{1}{4} x^{2} \\ c. & h (x) = 5 x^{2} \end{array} \end{aligned}$
::a.f(x)=3x2b.g(x)=14x2c.h(x)=5x2

Find the equation for a quadratic with vertex (8,2), going through the point (3,5).
::找到正经过点( 3, 5) 的顶部( 8, 2) 的二次方程。

Find the equation for a quadratic with vertex (-4,3) going through the point (9,-1).
::查找正穿过点(9,-1)的顶部(4,3)的二次方程。

Interactive
::交互式互动

Use the interactive below to transform other types of functions in vertex form. What happens when $\begin{aligned} a \end{aligned}$ is 0? Discuss why this happens.
::使用下面的交互效果来转换其他类型的顶点函数。当一个是 0 时会发生什么? 讨论为什么发生这种情况。

Activity 3: Converting from Vertex Form to Standard Form for a Quadratic
::活动3: 将二次曲线从螺纹格式转换为标准格式

Example 3-1
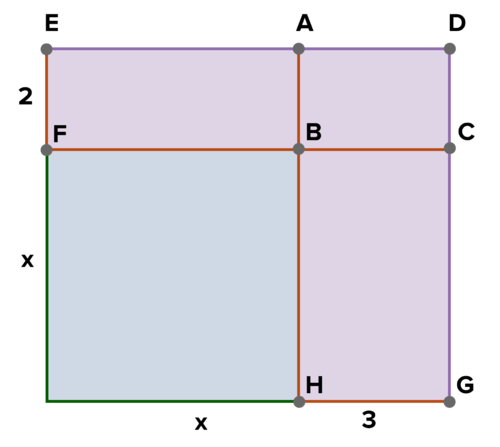
::例3-1

Previously, you learned to multiply two binomials using the area model. In order to perform the multiplication : $\begin{aligned} (x + 3) (x + 2), \end{aligned}$ draw a rectangle with dimensions as shown below, then find the area of each region and sum them. Use this method to write the area of the rectangle in expanded form .
::之前, 您学会了使用区域模型来乘法两个二进制。为了执行乘法 x+3)( x+2) , 请绘制以下尺寸的矩形, 然后找到每个区域的面积并将其相加。使用此方法以扩展的形式写入矩形的面积。

Solution:
::解决方案 :

\begin{aligned} (x + 2) (x + 3) = x^{2} + 5 x + 6 \end{aligned}

x+2(x+3)=x2+5x+6)

Example 3-2
::例3-2

Convert $\begin{aligned} y = 5 (x + 3)^{2} + 7 \end{aligned}$ to standard form .
::将 y=5 (x+3) 2+7 转换为标准格式。

Solution:
::解决方案 :

\begin{aligned} \begin{array}{ll} Equation & Explanation \\ y = 5 (x + 3)^{2} + 7 & Given equation. \\ y = 5 (x + 3) (x + 3) + 7 & Definition of squaring. \\ y = 5 (x^{2} + 6 x + 9) + 7 & Expanding using the area model. \\ y = 5 x^{2} + 30 x + 45 + 7 & Distribution of the 5. \\ y = 5 x^{2} + 30 x + 52 & Simplifying. \end{array} \end{aligned}

::QquationExplationy=5(x+3)2+7Felentn 等式.y=5(x+3)(x+3)+7 =5(x2+6x+9)+7 公式定义 y=5(x2+6x+9)+7 使用区域模型.y=5x2+30x+45+7 扩展 5.y=5x2+30x+52的分布简化。

Work it Out
::工作出来

Convert each of the following from vertex to standard form.
::将以下各项从顶部转换为标准表单。

$\begin{aligned} \begin{array}{ll} a. & y = (x - 5)^{2} \\ b. & y = - 2 (x + 4)^{2} \\ c. & y = 6 (x - 3)^{2} - 10 \end{array} \end{aligned}$
::ay=(x--5)2b.y=2(x+4)2c.y=6(x-3)2-10

The following quadratic functions are equivalent. Are any of their parameters equivalent? Why or why not? How do $\begin{aligned} a, h, and k \end{aligned}$ in vertex form affect $\begin{aligned} a, b, and c \end{aligned}$ in standard form? Explain.
::以下二次函数等同。它们的任何参数是否等同? 为什么或为什么不? 顶点形的 a、 h 和 k 如何影响标准格式的 a、 b 和 c? 解释。

\begin{aligned} \begin{array}{l} y = 3 (x - 4)^{2} + 5 \\ y = 3 x^{2} - 24 x + 53 \end{array} \end{aligned}

::y=3(x- 4) 2+5y=3x2- 24x+53

Interactive
::交互式互动

Use the interactive to experiment with changing the parameters of $\begin{aligned} a, b, and c \end{aligned}$ for the quadratic. Relate the observed changes to what you know about quadratic models as well as your understanding of the parameters for a quadratic in vertex form.
::使用交互性来实验改变a、b和c的参数, 用于二次曲线。将观察到的变化与您对二次曲线模型的了解以及您对顶点形态的二次曲线参数的理解相对应。

Summary
::摘要

Vertex Form for a Quadratic: $\begin{aligned} y = a (x - h)^{2} + k . \end{aligned}$ The vertex and vertical stretch factor are evident .
::二次曲线: y=a(x-h)2+k 的顶部和垂直伸展系数明显。

Standard Form for a Quadratic: $\begin{aligned} y = a x^{2} + b x + c . \end{aligned}$ The quadratic, linear, and constant terms are evident.
::二次曲线的标准表格: y=ax2+bx+c。二次曲线、线性和恒定值是显而易见的。

Section outline

General

二次曲线函数的垂直形态

The Purpose of this Lesson ::本课程的目的

Introduction: Vertical and Horizontal Shifts of Functions ::导言:职能的纵向和横向转移

Work it Out ::工作出来

Activity 1: Vertical Stretches ::活动1:垂直伸展

Example 1-1 ::例1-1

Changing the Leading Coefficient in a Quadratic Function ::在 Quadratic 函数中更改领导系数

PLIX Interactive ::PLIX 交互式互动

Activity 2: Changing the Leading Coefficient in a Quadratic Function ::活动2:在二次曲线函数中改变领导系数

Interactive ::交互式互动

Interactive ::交互式互动

Vertex Form for a Quadratic Function ::二次曲线函数的螺旋格式

Work it Out ::工作出来

Activity 3: Converting from Vertex Form to Standard Form for a Quadratic ::活动3: 将二次曲线从螺纹格式转换为标准格式

Example 3-1 ::例3-1

Work it Out ::工作出来

Interactive ::交互式互动

Summary ::摘要

The Purpose of this Lesson
::本课程的目的

Introduction: Vertical and Horizontal Shifts of Functions
::导言:职能的纵向和横向转移

Work it Out
::工作出来

Activity 1: Vertical Stretches
::活动1:垂直伸展

Example 1-1
::例1-1

Changing the Leading Coefficient in a Quadratic Function

::在 Quadratic 函数中更改领导系数

PLIX Interactive
::PLIX 交互式互动

Activity 2: Changing the Leading Coefficient in a Quadratic Function
::活动2:在二次曲线函数中改变领导系数

Interactive
::交互式互动

Interactive
::交互式互动

Vertex Form for a Quadratic Function
::二次曲线函数的螺旋格式

Work it Out
::工作出来

Activity 3: Converting from Vertex Form to Standard Form for a Quadratic
::活动3: 将二次曲线从螺纹格式转换为标准格式

Example 3-1
::例3-1

Work it Out
::工作出来

Interactive
::交互式互动

Summary
::摘要