4.9 有线性术语的四方-interactive
章节大纲
-
The Purpose of This Lesson
::本课程的目的In this lesson, you will explore the structure and behavior of quadratic functions that feature a linear term but no constant term. You'll explore different ways to represent such quadratics and develop tools to solve related equations.
::在此教训中, 您将探索二次函数的结构和行为, 二次函数具有线性术语, 但不具有恒定术语 。 您将探索不同的方式来代表这种二次函数, 并开发解决相关方程式的工具 。Introduction: Quadratic Functions with a Linear Term and no Constant
::导言:具有线性线性无常量的二次曲线函数Work it Out
::工作出来A speedboat on a river Consider an object accelerating at a constant rate , in a medium moving at a constant velocity : the distance the object has traveled as a function of time can be modeled with the equation y = 1 2 a x 2 + v 0 x . Suppose a speedboat is accelerating on a lake at 4 meters per second, per second. Create a function that models its distance as a function of time. Imagine the same boat on a river flowing at 3 meters per second. Create a model for the distance the boat in the river has traveled as a function of time. Graph both on the same axes. Discuss their characteristics. Although negative values are not in the practical domain , graph several points that show the of each parabola . Discuss their similarities and differences.
::以恒定速度, 以恒定速度移动的介质, 以恒定速度加速物体 : 该物体作为时间函数所穿行的距离可以与 y= 12ax2+v0x 等式模拟。 假设一艘快艇正在湖上加速, 每秒4米。 创建一个函数, 以时间函数来模拟它的距离。 想象一条河上同一艘船每秒3米。 创建一条河上船只作为时间函数所行距离的模型。 在同一轴上绘制两者的图。 讨论它们的特性。 尽管负值不是在实际的域中, 但用图表显示每个抛物体的距离。 讨论它们的相似性和差异 。Activity 1: Finding the Zeros of a Quadratic with no Constant
::活动1:寻找无常数的二次曲线的零点Interactive
::交互式互动Use the interactive below to explore the impact of changing the parameters for a quadratic of the form y = a x 2 + b x . Look specifically at how the quadratic changes as b is changed from 0 to non-0. How does the line of symmetry change? Adjust a so the quadratic has x - intercepts . How does the number of x -intercepts change as b goes from 0 to not 0? Adjust a to 1, and experiment with b . Look specifically at the line of symmetry and x -intercepts. How do they relate to b ?
::使用下面的互动来探索改变 y= ax2+bx 窗体四边形参数的影响。 请具体查看 b 的四方形变化是如何从 0 变为 非 0 的。 对称变化的线如何? 调整后四方形有 x intercuts 。 b 从 0 变为 0 的 x intercut 数字如何变化? 将 a 调整为 1 和 b 实验。 具体查看对称和 x intercuts 的线。 它们与 b 有何关系 ?Quadratics with a Linear Term and no Constant Term
::有线性线性、无固定期的四方形Such quadratics have the form y = a x 2 + b x .
::这种二次方形的形状为y=ax2+bx。They feature two x -intercepts, one of which is at the origin.
::它们有两个X接口,其中一个是源头。The x -intercepts are important elements of a quadratic function . They often have special significance in a scenario modeled by a quadratic, for example, signifying when or where an object hits the ground. If you know 2 x -intercepts, you can find the line of symmetry, that is, the x -coordinate for the vertex . And you'll soon see that solving any quadratic equation reduces to the process of finding x -intercepts. Because x -intercepts are the x -values that return values of 0 for the function, they are also called zeroes . Quadratics with a linear term and no constant term can be solved by factoring.
::x 界面是二次函数的重要元素。 在以二次方位模型为模型的假设情景中, 它们通常具有特殊意义, 例如, 表示一个对象何时或在哪里撞击地面。 如果您知道 2 x 界面, 您可以找到对称线, 即顶端的 X 坐标 。 您很快会看到任何二次方位的解析会降低到查找 x 界面的过程。 因为 X 界面是返回函数 0 值的 x 值, 它们也被称为 0 。 有线性术语和无常数术语的二次方位可以通过乘法解决 。Example 1-1
::例1-1Recall that the height of an object at a given time is modeled by the equation h ( x ) = 1 2 a x 2 + v 0 x + h 0 , where a is acceleration, v 0 is the initial velocity, and h 0 is the initial height. A ball is catapulted upward from ground level with an initial velocity of 40 meters per second. Acceleration due to gravity can be taken as -10 meters per second, per second. Create an equation to model the height of the ball as a function of time. Write and solve an equation to determine when the ball hits the ground. Determine the maximum height the ball achieves, and when that happens. Sketch a graph of the scenario.
::提醒注意一个对象在特定时间的高度是由公式 h( x) = 12ax2+v0x+h0 模拟的,其中 a 是加速度, v0 是初始速度, h0 是初始高度。 一个球从地面向上投出,初始速度为每秒40米。 重力加速可以以每秒10米的速度加速。 创建一个公式, 以模拟球的高度作为时间函数。 写入并解析一个公式, 以确定球何时撞击地面。 确定球达到的最高高度, 以及何时发生。 绘制一个场景图 。Solution: The equation is: h ( x ) = − 5 x 2 + 40 x .
::解答: 方程式是: h(x)\\\\\"5x2+40x.To determine when the ball hits the ground, solve for a ball height, h ( x ) , of zero:
::要确定球何时击中地面, 解答球高度, h(x), 零 :− 5 x 2 + 40 x = 0
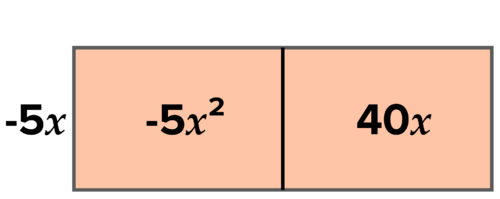
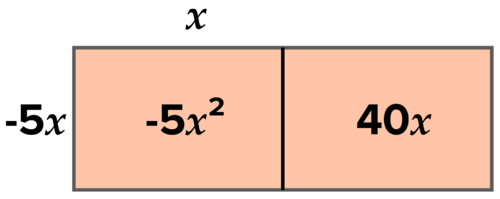
::-5x2+40x=0To solve this equation by factoring, look for the greatest common factor in both terms . You may wish to use a rectangle as shown below to organize your work. Each term is divisible by − 5 x :
::要通过乘数来解析此等式, 请在两个词中寻找最大的共同系数。 您可能希望使用下面显示的矩形来组织您的工作。 每个词可以用 - 5x 进行变换 :Factor out the GCF of -5x squared and 40x
::将 - 5x平方和 - 40的绿色气候基金计算出来What do you need to multiply − 5 x by to get − 5 x 2 ? See below:
::您需要多少乘以 5x 才能获得 5x2 ? 见下文:-5x squared divided by -5x is x
::-5x 平方除以 -5x xWhat do you need to multiply − 5 x by to get 40 x ? See below:
::要获得40x, 您需要乘以 ~ 5x 多少才能获得40x ? 见下面:40x divided by -5x is 8
::40x 40 除以 -5x除以 -5x为 8Now you can write the function in factored form :
h ( x ) = − 5 x 2 + 40 x h ( x ) = − 5 x ( x − 8 )
::现在您可以以系数格式写入函数 : h( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\This means you can re-write the equation from above:
::这意味着您可以从上面重写方程式 :− 5 x 2 + 40 x = 0 − 5 x ( x − 8 ) = 0
::-5x2+40x=0-5x(x-8)=0The factored form of the equation shows a product of two expressions equal to 0. If you can find an x -value that makes either of the two expressions 0, the product will be 0, and the equation will be true for that value. This is called the Zero Product Property . You can write two separate equations to accomplish this:
::公式的系数形式显示两个表达式等于 0 的产物。如果能找到一个 X 值使两个表达式 0 中的任何一个成为 0,则该产品将为 0,而该等值的方程式将是真实的。这称为“零产品属性”。为此,您可以写两个不同的方程式:First Equation Second Equation Explanation − 5 x = 0 x − 8 = 0 Equations to set each factor equal to 0. x = 0 x = 8 Solving. − 5 ( 0 ) ( 0 + 8 ) = 0 − 5 ( 8 ) ( 8 − 8 ) = 0 Substitute these values into the equation to confirm. ( 0 ) ( 8 ) = 0 ( − 40 ) ( 0 ) = 0 Simplifying. 0 = 0 0 = 0 Solution confirmed.
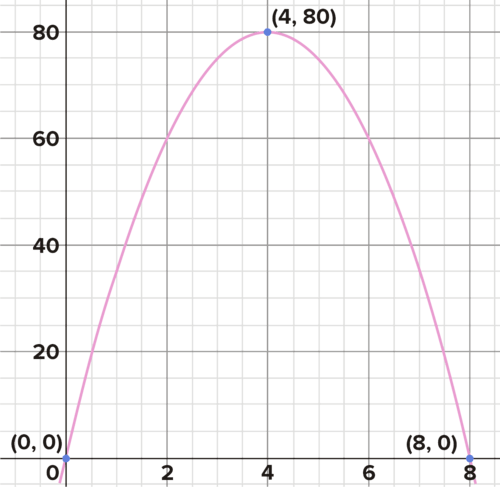
::第一次等式解释 - 5x=0x-8=0等量确定每个系数等于 0.x=0x=8Scolving.- 5(0(0+8)=0- 5(8)(8-8)=0在方程中设置这些值以确认 .(0)(8)=0(-40)(0)=0简化.0=00=0The two zeroes are 0 and 8. The ball hits the ground at 8 seconds. The line of symmetry is halfway between these values, at x = 4. The vertex is found by substituting this value into the function:
::两个零是 0 和 8 。 球在 8 秒内击中地面。 对称线是这些值之间的一半, 在 x= 4 。 顶点通过将此值替换为函数来找到 :h ( 4 ) = − 5 ( 4 ) ( 4 − 8 ) h ( 4 ) = − 20 ( − 4 ) h ( 4 ) = 80
::h(4) 5(4)(4-8)h(4) 20(-4)h(4)=80The vertex is (4,80). At 4 seconds the ball reaches its greatest height, 80 meters:
::顶部是(4,80) 4秒后 球达到最大高度80米At 4 seconds, the ball reaches its maximum height of 80 meters Zeroes, Factored Form, and the Zero Product Property
::零、计数表格和零产品属性The zeroes of a function are the x -intercepts.
::函数的零是 X 界面。Factored form for a quadratic shows the quadratic as a product of two linear expressions.
::二次方形的乘数表显示二次方形为两个线性表达式的产物。The zero product property means that if you find a value that makes a factor 0, you've found a zero.
::零产品属性意味着,如果你发现一个值 使因数0, 你就会发现一个零。Work it Out
::工作出来-
A ball is
catapulted
upward from ground level with an initial velocity of 65 meters per second. Acceleration due to gravity can be taken as -10 meters per second, per second. Create an equation to model the height of the ball as a function of time. Write and solve an equation to determine when the ball hits the ground. Determine the maximum height the ball achieves and when that happens. Sketch a graph of the scenario.
::从地面向上投出一个球,初始速度为每秒65米。 重力加速可以以 - 10米/秒/秒/秒/ 秒/ 秒/ 10米/ 秒/ 秒/ 秒/ 秒/ 秒的速度加速 。 创建一个方程式, 将球的高度作为时间函数来建模 。 写入和解析一个方程式, 以确定球何时撞击地面。 确定球达到的最大高度和何时达到最大高度。 绘制一个场景图 。 -
Determine the zeroes and vertex for each of the following quadratics, and sketch the graphs. Some may not have zeroes.
::确定以下各象形的零和顶点,并绘制图形。有些可能没有零。
a. a ( x ) = x 2 + 2 x b. b ( x ) = − 3 x 2 + 12 x c. c ( x ) = − 7 x 2 − 49 x d. d ( x ) = 2 x 2 + x e. p ( x ) = 10 x 2 − 3 x f. f ( x ) = − 3 x 2 + 7 x g. g ( x ) = 1 6 x 2 − 12 h. h ( x ) = − 0.1 x 2 i. q ( x ) = x 2 + 5
::a. a. a. (x) =x2+2xb. b. b. (x) 3x2+12xc. c. (x) =7x2- 49xd. d. (x) =2x2+xe. p. (x) =10x2 - 3x2 - 3xf. f. (x) =3x2+7xxg. g(x) =16x2 - 12h.h(x) =0.1x2i.q (x) =x2+5
Activity 2: Building Quadratic Functions from Zeroes and an Additional Point
::活动2:从零和额外点建立四分函数If you know two zeroes for a quadratic and one more point, you can find the equation for the quadratic. Remember that all the quadratics in this section have a zero at the origin and one other zero. All such quadratics have the form y = a x 2 + b x . Confirm this with the following interactive as needed. Discuss why this is the case.
::如果您知道一个二次方块和另一个点的两零, 您可以找到二次方块的方程 。 记住本节中的所有二次方块在源头有一个零, 其它一个零。 所有此类方块都有 y= ax2+bx 的形态。 请按需要用以下交互方式确认这一点 。 讨论为何如此 。Example 2-1
::例2-1A baseball is launched from the origin. It lands at a point 10 meters away. During its flight, a photograph is taken showing the baseball at the point (2,5). Find the equation which models the flight path of the baseball. Determine the highest point on its trajectory.
::棒球是从原点开始的。 它降落在距离10米的地方。 在飞行过程中, 拍摄了一张照片显示棒球在点(2, 5) 。 找到模拟棒球飞行路径的方程式。 确定它轨道上的最高点 。Solution: Use the function h ( x ) = a x 2 + b x . Substituting the point (0,0) here doesn't create a useful equation. (Try it to confirm that.) However, if you substitute (10,0) and (2,5), you get the following system:
::解析度 : 使用函数h( x) = ax2+bx。 替换点( 0,0)在这里不会产生有用的方程式 。 (试着确认这一点 。) 但是, 如果您替换了( 10,0) 和(2, 5) , 您可以得到以下系统 :a ( 10 ) 2 + b ( 10 ) = 0 a ( 2 ) 2 + b ( 2 ) = 5
::a(10)2+b(10)=0a(2)2+b(2)=5Simplifying and re-arranging:
::简化和重新排列:100 a + 10 b = 0 4 a + 2 b = 5
::100a+10b=04a+2b=5Dividing each to reduce the size of the coefficients:
::为减少系数的大小而各分配:1 10 ( 100 a + 10 b = 0 ) 1 2 ( 4 a + 2 b = 5 )
::110(100a+10b=0)12(4a+2b=5)10 a + b = 0 2 a + b = 5 2
::10a+b=02a+b=52Subtraction gives:
::减法给出 :8 a = − 5 2 a = − 5 16
::8a52a516Substitution gives:
::替代条件:10 ( − 5 16 ) + b = 0 b = 25 8
::10(516)+b=0b=258So the function is:
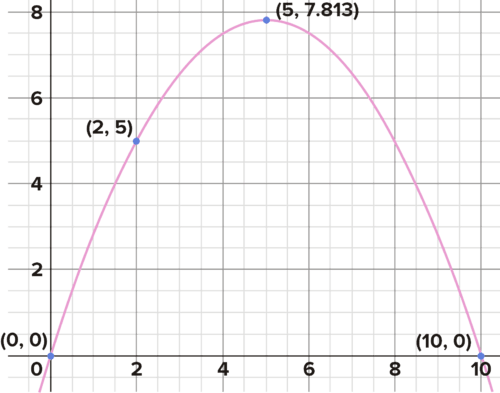
::因此,该函数是:y = − 5 16 x 2 + 25 8 x
::y516x2+258xThe line of symmetry is halfway between the zeroes of 0 and 10, that is,
::对称线介于0和10的零之间,即x=5。
::要找到顶点 :h ( 5 ) = − 5 16 ( 5 ) 2 + 25 8 ( 5 ) h ( 5 ) = − 125 16 + 125 8 h ( 5 ) = 125 16 h ( 5 ) = 7 13 16 ( 5 , 7 13 16 )
::h(5)516(5)2+258(5)h(5)=12516+1258h(5)=12516h(5)=71316(5,71316)A baseball is launched from the origin. It lands at a point 10 meters away. Building Quadratic Functions from Zeroes and an Additional Point
::从零点和额外点开始的二次曲线函数If one of the zeroes is at the origin, the form for the function is y = a x 2 + b x .
::如果一个零是源值,函数的窗体为y=ax2+bx。Substituting the second zero into the equation and the additional point gives you a system of linear equations you can use to solve for a and b .
::将第二个零替换为方程, 附加点为您提供一个线性方程系统, 您可以用以解答 a和 b 。Write the equation for the function using these values.
::使用这些值写入函数的方程式。Interactive
::交互式互动For the following interactive, use the sliders to change the stretch factor a and the non-zero zero . Record your observations.
::用于以下交互式互动的,使用滑动符来更改伸缩系数a和非零。记录您的观察结果。Work it Out
::工作出来-
A skate park features a bowl sunk into the ground. A side view shows the arc of the bowl to be parabolic. Let one edge of the bowl be the point (0,0) and the other the point (8,0). The bowl passes through the point (2,-2). Find the equation for the quadratic function for the bowl, and find the lowest point of the bowl. Sketch a graph.
::滑冰公园将一个碗面投进地表。 侧面视图显示碗的弧形是抛物线。 让碗边的一个边缘是点( 0,0), 另一个边缘是点( 8,0)。 碗面通过点(2, 2) 。 找到碗面的二次函数方程式, 并找到碗底的最小点。 绘制一个图 。 -
Given a quadratic in the form
f
(
x
)
=
a
x
2
+
b
x
, factor out
a
x
.
Write the quadratic in factored form. What are the zeroes? What is the line of symmetry? What is the
x
-coordinate of the vertex? (All your answers here will be in terms of
a
and
b
.
)
::给定 f( x) = ax2+bx 中的四方形, 因数输出 ax 。 以系数形式写入二次方形。 零是什么? 对称线是什么? 顶端的 x 坐标是什么 ? (这里所有的答案都是 a 和 b ) -
Use your observations in the last problem to find the line of symmetry for
y
=
3
x
2
+
2
x
.
::使用您对上一个问题的观察来找到 y= 3x2+2x 的对称线 。
Finding the Line of Symmetry from Zeroes
::从零点寻找对称线Given f ( x ) = a x 2 + b x :
::给定 f( x) = 轴2+bx :-
The zeroes are 0 and
−
b
a
.
::零是0和-ba。 -
The line of symmetry is half the value of the second zero, that is,
x
=
−
b
2
a
.
::对称线是第二个零的值的一半,即 xb2a。 -
The line of symmetry is the
x
-coordinate of the vertex.
::对称线是顶点的 X 坐标 。
-
(extension) The quadratic
y
=
(
x
+
3
)
2
−
9
is in vertex form. What is the vertex? Write an equation, then use
inverse
operations
and properties of equality to find the zeroes. If you have done your work correctly, one of the zeroes is at the origin. But if a quadratic has two zeroes and one is at the origin, it has the form
y
=
a
x
2
+
b
x
.
How is this possible? Convert
y
=
(
x
+
3
)
2
−
9
from vertex to
standard form
. (Hint: Begin by using the area model for distribution to square
x
+
3.
) What do you observe? Is this
consistent
with your calculation of the zeroes? Explain.
::等离子 y = (x+3) 2- 9 以顶点形式出现。 顶点是什么 ? 写一个方程, 然后使用反向操作和等同属性来找到零。 如果您做了正确的工作, 一个零就是源头。 但是如果一个四面点有两个零, 一个在源头, 它有 y= ax2+bx 。 这怎么可能? 将 y = (x+3) 2- 9 从顶点转换为标准格式 。 (hint: 开始使用区域模型将分布为平方 x+3 ) 你观察什么? 这是否与您计算零一致? 解释 。 -
Solve each equation below using methods from this and prior lessons. For the first few, the initial objective is to write
the equation
in the form
a
x
2
+
b
x
=
0.
Why?
::使用此课和先前课中的方法在下面解析每个方程式。 对于前几个方程式,最初的目标是以x2+bx=0的形式写出方程式。 为什么?
a. x 2 + 5 x = 0 b. 3 x 2 + 10 x = 4 x c. 5 x 2 − 7 x = 3 x 2 + x d. 12 x 2 + 4 x − 7 = 7 x 2 − x − 7 e. x 2 = 9 f. 8 x 2 − 49 = 0
::a.x2+5x=0b.3x2+10x=4xc.5x2-7x=3x2+x12x2+4x-7=7x2-7e.x2=9f.8x2-49=0Summary
::摘要-
Quadratics with a linear term but no constant term can be factored to find the zeroes, one of which will be 0.
::有线性术语但无常值术语的四边形无法计算以找到零, 其中之一是 0 。 -
Halve the value of the zero that's not 0 and you've got the line of symmetry, that is, the
x
-coordinate of the vertex.
::将零的值减半,那不是0, 你已经得到了对称线, 也就是说, 脊椎的X坐标。 -
Many quadratic equations can be solved by re-arranging them so that you've got a quadratic expression equal to 0, then factoring.
::许多四方方程式可以通过重新排列来解答, 这样您就可以有等于 0 的四方方程式表达式, 然后算术 。
-
A ball is
catapulted
upward from ground level with an initial velocity of 65 meters per second. Acceleration due to gravity can be taken as -10 meters per second, per second. Create an equation to model the height of the ball as a function of time. Write and solve an equation to determine when the ball hits the ground. Determine the maximum height the ball achieves and when that happens. Sketch a graph of the scenario.